Распределение Парето в теории вероятностей — двухпараметрическое семейство абсолютно непрерывных распределений, являющихся степенными. Когда вероятность получения того или иного значения обратно пропорциональна некоторой степени этого значения, то данная величина характеризуется степенным законом. Проще говоря, это один из главных математических законов нашей жизни. Он выглядит так:
Степенные законы часто встречаются в физике, биологии, науках о Земле, космосе, экономике, финансах, информатике, демографии и прочих социальных науках [см. Guerriero, V. (2012). "Power Law Distribution: Method of Multi-scale Inferential Statistics". Journal of Modern Mathematics Frontier (JMMF), 1: 21-28., а также "M. E. J. Newman Power laws, Pareto distributions and Zipf’s law"].
Степенному закону подчиняются размеры кратеров на Луне, население городов на Земле, силы землетрясений, размеры компьютерных файлов, масштабы военных конфликтов, частоты слов в любом человеческом языке, частоты фамилий в большинстве культур, продажи товаров почти любой категории с многими торговыми марками, число видов в биологическом роде, число статей, которые пишут учёные, число переходов на веб-страницы.
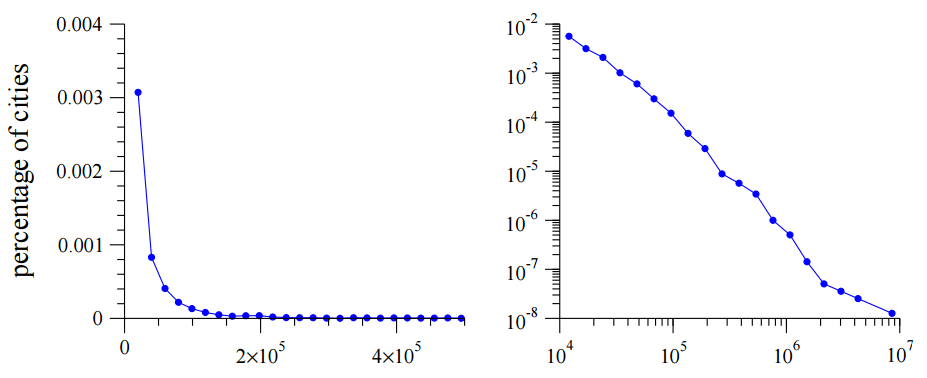
Гистограммы населённых пунктов США по числу жителей (число жителей отложено по оси абсцисс)
И конечно же, степенному закону подчиняется распределение благосостояния людей.
Итальянский инженер и экономист Вилфредо Парето разработал свою теорию изначально для описания распределения благосостояния, а также распределения доходов людей в обществе. По мысли Парето, общество имеет пирамидальную структуру, на вершине которой находится элита — руководящий социальный слой, направляющий жизнь всего общества. В своих работах Парето скептически относился к демократическим режимам. Учёный полагал, что в политической жизни есть универсальный закон, при котором элита всегда обманывает массы.
В одной из своих работ Вилфредо Парето заметил, что 20% итальянских домохозяйств получают 80% доходов. Хотя учёный умер в 1923 году, в 1941 году в его честь решили назвать так называемый «закон Парето» о том, что 20% труда реализуют 80% результата, но остальные 20% результата требуют 80% общих затрат. Как видим, распределение Парето и степенные законы опять проявили себя.
Если мы предполагаем, что распределение благосостояния в обществе подчиняется степенному закону, то мы косвенно подтверждаем правомочность теории элит, о которой говорил сам Парето.
Так или иначе, но капиталистическое западное общество в полной мере демонстрирует правомочность этой теории. Благосостояние людей действительно подчиняется степенному закону. Самое наглядное подтверждение этому мы можем получить, если изучим распределение биткоинов по кошелькам.
Блокчейн позволяет в подробнейшим образом изучить путь каждой монеты: зафиксировать, когда она появилась, через какие кошельки прошла и в каком кошельке находится сейчас. Из-за анонимной сущности системы мы не можем сделать вывод о количестве пользователей системы или благосостоянии каждого из них, но распределение монет по кошелькам демонстрируется точнейшим образом.
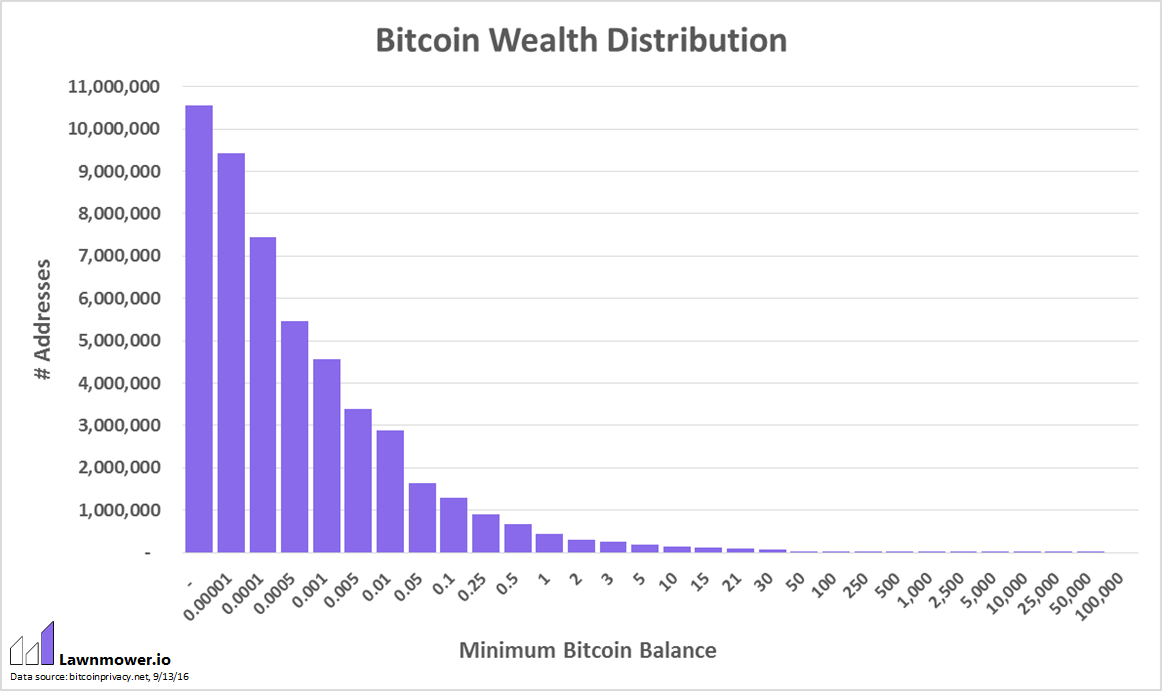
В абсолютных цифрах получается следующая картина:
 7,4 млн адресов с балансом >0,0001 BTC ($0,06)
7,4 млн адресов с балансом >0,0001 BTC ($0,06)
4,5 млн адресов с балансом >0,001 BTC ($0,61)
2,8 млн адресов с балансом >0,01 BTC ($6,08)
1,2 млн адресов с балансом >0,1 BTC ($60,80)
446 301 адрес с балансом >1 BTC ($608)
131 709 адресов с балансом >10 BTC ($6080)
13 698 адресов с балансом >100 BTC ($60 800)
1658 адресов с балансом >1000 BTC ($608 000)
121 адрес с балансом >10 000 BTC ($6 080 000)
1 адрес с балансом >100 000 BTC ($60 800 000)
Подробная статистика приведена в таблице.
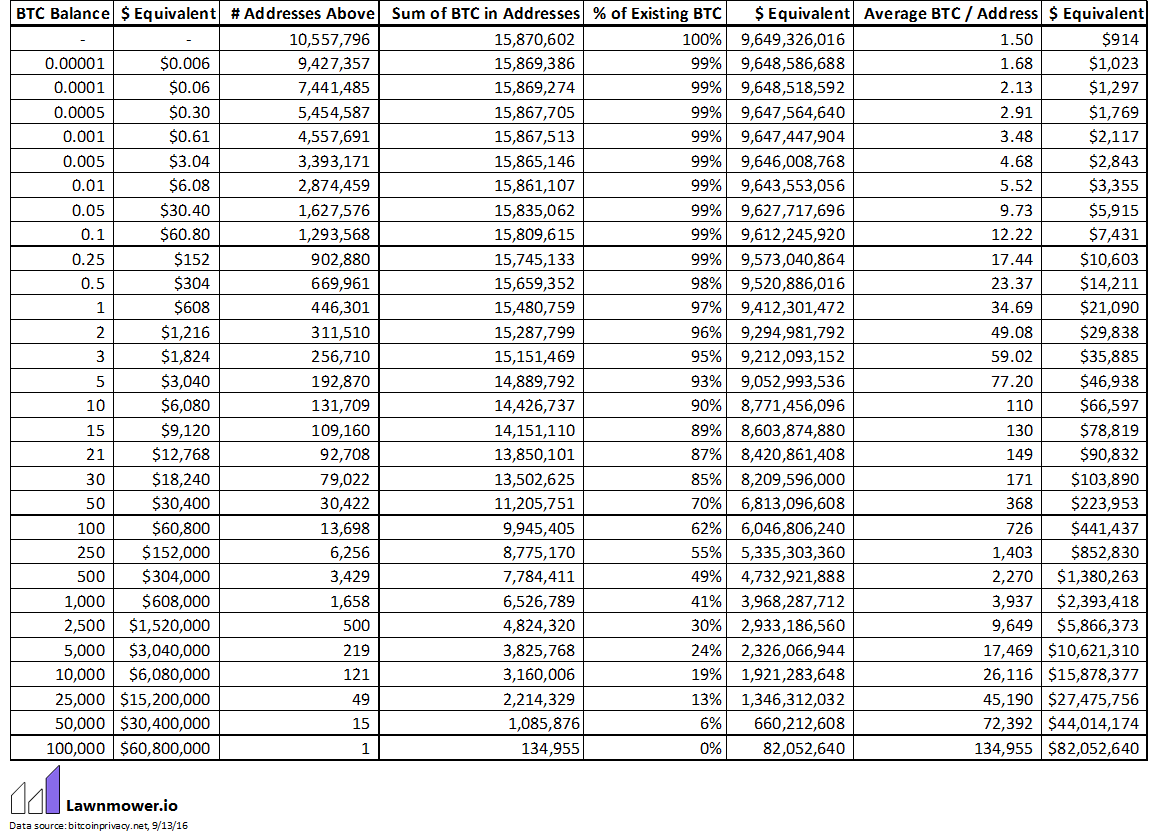
Налицо практически идеальное степенное распределение.
Как уже упоминалось, по количеству кошельков нельзя судить о количестве пользователей Bitcoin. Одному человеку может принадлежать много кошельков. И наоборот, группа лиц (или юридическое лицо) может совместно владеть одним кошельком с крупной суммой.
Тем не менее, исходя из других косвенных свидетельств, можно сделать вывод, что биткоинами во всём мире пользовалось примерно 7 миллионов человек. Правда, общее количество пользователей может быть размазано во времени. Некоторые исследователи предполагают, что до 30% существующих пользователей биткоинов являются «зомби», потерявшими свои приватные ключи и доступ к денежным средствам. Неизвестна и судьба Сатоси Накамото, который намайнил миллион монет на своём персональном компьютере на заре становления системы.
Как показало расследование, c 3 января 2009 года по 25 января 2010 года майнингом биткоинов занимался практически только один человек, и абсолютное большинство добытых в то время монет хранятся у него до сих пор.
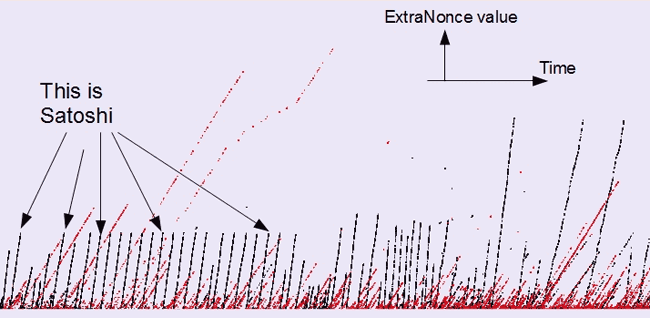
Чёрным и красным цветами показана генерация и трата монет в промежутке между блоками 1 и 36288
Конечно, нельзя на 100% утверждать, что сгенерированные в первое время монеты принадлежат Сатоси, но факт в том, что некто начал майнинг с первого блока и продолжал его целый год на стабильной скорости около 7 мегахэшей в секунду, с небольшими паузами примерно каждые 100 часов, предположительно, для резервного копирования кошелька.
По оценкам, Сатоси в первые месяцы добыл около 1 миллиона монет, что составляет около 602 миллионов долларов по текущему курсу.
p(x) = Cx-m
Степенные законы часто встречаются в физике, биологии, науках о Земле, космосе, экономике, финансах, информатике, демографии и прочих социальных науках [см. Guerriero, V. (2012). "Power Law Distribution: Method of Multi-scale Inferential Statistics". Journal of Modern Mathematics Frontier (JMMF), 1: 21-28., а также "M. E. J. Newman Power laws, Pareto distributions and Zipf’s law"].
Степенному закону подчиняются размеры кратеров на Луне, население городов на Земле, силы землетрясений, размеры компьютерных файлов, масштабы военных конфликтов, частоты слов в любом человеческом языке, частоты фамилий в большинстве культур, продажи товаров почти любой категории с многими торговыми марками, число видов в биологическом роде, число статей, которые пишут учёные, число переходов на веб-страницы.

Гистограммы населённых пунктов США по числу жителей (число жителей отложено по оси абсцисс)
И конечно же, степенному закону подчиняется распределение благосостояния людей.
Итальянский инженер и экономист Вилфредо Парето разработал свою теорию изначально для описания распределения благосостояния, а также распределения доходов людей в обществе. По мысли Парето, общество имеет пирамидальную структуру, на вершине которой находится элита — руководящий социальный слой, направляющий жизнь всего общества. В своих работах Парето скептически относился к демократическим режимам. Учёный полагал, что в политической жизни есть универсальный закон, при котором элита всегда обманывает массы.
В одной из своих работ Вилфредо Парето заметил, что 20% итальянских домохозяйств получают 80% доходов. Хотя учёный умер в 1923 году, в 1941 году в его честь решили назвать так называемый «закон Парето» о том, что 20% труда реализуют 80% результата, но остальные 20% результата требуют 80% общих затрат. Как видим, распределение Парето и степенные законы опять проявили себя.
Если мы предполагаем, что распределение благосостояния в обществе подчиняется степенному закону, то мы косвенно подтверждаем правомочность теории элит, о которой говорил сам Парето.
Так или иначе, но капиталистическое западное общество в полной мере демонстрирует правомочность этой теории. Благосостояние людей действительно подчиняется степенному закону. Самое наглядное подтверждение этому мы можем получить, если изучим распределение биткоинов по кошелькам.
Блокчейн позволяет в подробнейшим образом изучить путь каждой монеты: зафиксировать, когда она появилась, через какие кошельки прошла и в каком кошельке находится сейчас. Из-за анонимной сущности системы мы не можем сделать вывод о количестве пользователей системы или благосостоянии каждого из них, но распределение монет по кошелькам демонстрируется точнейшим образом.

В абсолютных цифрах получается следующая картина:
 7,4 млн адресов с балансом >0,0001 BTC ($0,06)
7,4 млн адресов с балансом >0,0001 BTC ($0,06)4,5 млн адресов с балансом >0,001 BTC ($0,61)
2,8 млн адресов с балансом >0,01 BTC ($6,08)
1,2 млн адресов с балансом >0,1 BTC ($60,80)
446 301 адрес с балансом >1 BTC ($608)
131 709 адресов с балансом >10 BTC ($6080)
13 698 адресов с балансом >100 BTC ($60 800)
1658 адресов с балансом >1000 BTC ($608 000)
121 адрес с балансом >10 000 BTC ($6 080 000)
1 адрес с балансом >100 000 BTC ($60 800 000)
Подробная статистика приведена в таблице.

Налицо практически идеальное степенное распределение.
Как уже упоминалось, по количеству кошельков нельзя судить о количестве пользователей Bitcoin. Одному человеку может принадлежать много кошельков. И наоборот, группа лиц (или юридическое лицо) может совместно владеть одним кошельком с крупной суммой.
Тем не менее, исходя из других косвенных свидетельств, можно сделать вывод, что биткоинами во всём мире пользовалось примерно 7 миллионов человек. Правда, общее количество пользователей может быть размазано во времени. Некоторые исследователи предполагают, что до 30% существующих пользователей биткоинов являются «зомби», потерявшими свои приватные ключи и доступ к денежным средствам. Неизвестна и судьба Сатоси Накамото, который намайнил миллион монет на своём персональном компьютере на заре становления системы.
Как показало расследование, c 3 января 2009 года по 25 января 2010 года майнингом биткоинов занимался практически только один человек, и абсолютное большинство добытых в то время монет хранятся у него до сих пор.

Чёрным и красным цветами показана генерация и трата монет в промежутке между блоками 1 и 36288
Конечно, нельзя на 100% утверждать, что сгенерированные в первое время монеты принадлежат Сатоси, но факт в том, что некто начал майнинг с первого блока и продолжал его целый год на стабильной скорости около 7 мегахэшей в секунду, с небольшими паузами примерно каждые 100 часов, предположительно, для резервного копирования кошелька.
По оценкам, Сатоси в первые месяцы добыл около 1 миллиона монет, что составляет около 602 миллионов долларов по текущему курсу.
Поделиться с друзьями
Комментарии (6)

starius
26.09.2016 02:46В статье рассматривается распределение по адресам, но одному человеку могут принадлежать сотни адресов, на каждом из которых мало средств. Отчасти этому способствует то, что многие реализации bitcoin кладут сдачу от переводов на новые адреса.

eugzol
26.09.2016 02:54Вот именно. Не удивлюсь, если окажется, что в посте описано не применение некоего вселенского мудрого закона к биткоинам, а попросту некое тождество, вытекающее из способа работы современных биткоин кошельков и/или артефактов исторического развития сети.

elite7
26.09.2016 11:54Не совсем понятно, что такое ExtraNonce value, что такое красные линии, чем они отличаются от черных и как определили, что черные принадлежат Сатоши.


quantuz
Хм, читал, чуть ли не на Гиктаймсе, что закон Парето лженеаучен…
vics001
Да, конечно, бред. Не знаешь, какое распределение — говори Парето, оно же степенное, оно же Zipfa. Все это строится на простой математической штуке, если мы возьмем кумулятивное распределение, то получится график от 0 до 1, в квадрате [0, 1[ x [0, 1[, который всегда проходит надо прямой x=y и который очень часто крайне выпуклый. Пересекая этот график с прямой x= 1 — y, получаем наши красивые распределения 2%людей владеют 98% ресурсов, за счет этой выпуклости достигается дисбаланс, чем больше выпуклость, тем больше дисбаланс. Причем, откидывая хвост или голову распределения, выпуклость все равно сохраняется.
А почему, все же, это распределение так нравится (математически абсолютно правильная формула и может иметь смысл), потому что описывается красиво. 10-й по рангу объект приблизительно в 10 раз реже встречается, чем 1-й и т.п. Но если подумать, это «приблизительно» верно для абсолютно все распределений, только если проверять стандартными способами, то они даже близко не подходят. Но его все равно любят экономисты и лингвисты.
Конкретно по этой таблице, по такому закону, разница между двумя соседними ячейками в колонке Sum of BTC, должна быть приблизительно одиникава, но что видно, что где-то в начале таблицы она действительно около 1 000 000, то в конце ничего и близко похожего нет. Так что заявление «Налицо практически идеальное степенное распределение», полная профанация. Тут даже ошибка по формуле не посчитана и 2 константы не приведены.
avost
А нет никакого закона. Есть «правило Парето». И оно с одной стороны полуэмпирическое (и «действует» постфактум, когда говорят — о, смотри, и эта штука подчиняется правилу Парето), ас другой — полушутливое (в том же смысле, что и «законы Мерфи» ).