 » alt=«image»/>
» alt=«image»/>Считаю уместным показать доказательство Большой теоремы Ферма (БТФ) для третьей степени.
Во-первых: каждая степень может рассматриваться аналогично.
Во-вторых: до сих пор нет доказательства для куба, основанного на возможностях элементарной математики.
И, кроме того, ввиду более упрощённых расчётов, за счёт величины числовых значений, рассмотрение куба может оказаться более доступным для понимания.
Благодарю, заранее, возможных оппонентов, за полезные замечания в оформлении доказательства, и, конечно, за помощь.
И ещё немного желчи.
В восприятии доказательства на Математическом форуме dxdy МГУ нет признаков понимания доказательства.
При этом необходимо заметить, что там сосредоточена часть математической общественности, занимающаяся проблемой БТФ продолжительное время, и даже, профессионально.
Это на форуме dxdy потребовали, чтобы доказательство основывалось на рассмотрении куба.
Не помогло. Но считаю, такое требование полезным.
Спрашивал: «Чего не хватает? Что требуется ещё рассмотреть?»
Молчание, или в лучшем случае рекомендации: доказать то, что, уже давно доказано, и, несомненно, оппонентам известно. И, кроме этого, тема на форуме dxdy прикрыта.
Её можно там читать, но отсутствует обратная связь
Может быть, кто-то на Хабрхабре конкретизирует требования.
Хочется услышать мнение.
Доказательство может считаться справедливым, если оно удовлетворяет условия:
1. Показатель степени n – простое число. [1]
Рассмотрим доказательство Большой теоремы Ферма при рассмотрении уравнения Ферма для куба.
Необходимо доказать, что

при целочисленных
 невозможно.
невозможно.I. Два случая Большой теоремы Ферма (БТФ).
I.1 К первому случаю БТФ относятся разности точных степеней с произвольными основаниями, за исключением оснований, обеспечивающих 2 Случай БТФ.
Имеют место:
Имеют место:
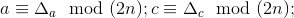
 — взаимно простые числа, а основание b
— взаимно простые числа, а основание b 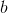 – чётное.
– чётное.Именно, по этому варианту, требуется найти доказательство.
1.2 Выразим основания равенства 1.1 через единые аргументы, для чего вводим следующие обозначения:
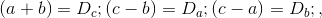
где, например,
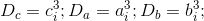
где
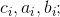 — целые числа. [2]
— целые числа. [2]1.3 Поэтому равенство 1.1 может быть представлено в виде:
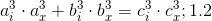
или
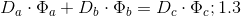
где:

2.1 И первый случай БТФ, и второй случай БТФ доказываются на основании соизмеримости степеней и их оснований по
 .
.Доказательство построено на сопоставлении величин:
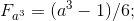 — со измеритель степени и
— со измеритель степени и — со измеритель основания.
— со измеритель основания.2.2 При доказательстве первого случая БТФ при использовании
 и классов вычетов 1 и 5, можем выразить основания
и классов вычетов 1 и 5, можем выразить основания  :
: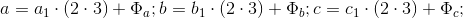
где:
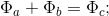
При этом
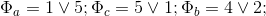
2.3 При рассмотрении первого случая БТФ, когда
 , основания
, основания  может принадлежать к первому или пятому классам вычетов, а основание
может принадлежать к первому или пятому классам вычетов, а основание  — наоборот.
— наоборот. Потому что, основания, принадлежащие к чётным классам вычетов, не подходят, как и основания, принадлежащие к 3-у классу вычетов, так как в этом случае во всех основаниях возникают общие множители, что противоречит условиям теоремы.
2.4 При рассмотрении оснований степеней, принадлежащих к конкретному классу вычетов, корректировка величин оснований в уравнении Ферма зависит только от

И для второго случая БТФ тоже.
Особенности первого и второго случаев БТФ влияют на расчётную закономерность, но принципиального значения для доказательства не представляют.
3.1 При рассмотрении доказательства второго случая БТФ выбор класса вычетов для оснований
 и
и 
значения не имеет, так как всегда можно использовать перевод любого из оснований к первому классу вычетов, используя для этого сомножитель, равный точной степени, на основании возможности перевода любого класса вычетов, взаимно простого с показателем рассматриваемой степени. (Малая теорема Ферма).
Поэтому, при рассмотрении второго случая БТФ достаточно рассмотрение варианта, когда

3.2 Для второго случая БТФ:
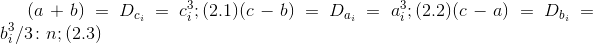
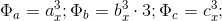
и
 , где
, где — положительное число натурального числового ряда, взаимно простое с величиной.
— положительное число натурального числового ряда, взаимно простое с величиной. 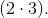
4.1 Рассмотрим доказательство второго случая БТФ.
. Установленные закономерности:
Сомножители, присутствующие в
 , присутствуют и в
, присутствуют и в  .
. Пример 1:

Пример 2:

Пример 3:

Пример 4:

4.2 Деление
 на сомножители, присутствующие в
на сомножители, присутствующие в , обеспечивает целочисленное частное, принадлежащее к первому классу вычетов по
, обеспечивает целочисленное частное, принадлежащее к первому классу вычетов по 

5.1 Пример расчёта разности степеней
(первый):

Число второго класса вычетов – не подходит.
И это величина, которая должна содержать величину

При этом,

должен содержать дополнительный сомножитель.
5.2 Пример расчёта разности степеней (второй):

А если добавить в разность оснований степеней, как сомножитель, точный куб, относящийся, также, к пятому классу вычетов по
 ,
,дополнительный сомножитель, равный основанию введённого куба в

не возникает.,
5.3 Пример расчёта разности степеней (третий):

Возникает вопрос: Какие сомножители, присутствующие в
 могут быть отнесены к сомножителям величины a_1.
могут быть отнесены к сомножителям величины a_1.5.4 Итак,
 обязательно, делится на
обязательно, делится на  обеспечивая частное, относящееся к первому классу вычетов по
обеспечивая частное, относящееся к первому классу вычетов по 
5.5 Введенная в разность
 степень
степень  , относящаяся к пятому классу вычетов по
, относящаяся к пятому классу вычетов по
обеспечивает возникновение в величине
 сомножитель
сомножитель  сомножитель, равный основанию степени, введенной в разность между основаниями.
сомножитель, равный основанию степени, введенной в разность между основаниями. Пример 1:

Назовём эти сомножители замеченными сомножителями.
Замеченные сомножители рассматриваются нами, как сомножители, обеспечивающие частное
 обязательно, относящееся к пятому классу вычетов, по
обязательно, относящееся к пятому классу вычетов, по
.
6.1 На основании найденных закономерностей, переходим к анализу разности степеней с целью ответа на вопрос:
Когда величина
 может содержать сомножитель
может содержать сомножитель  ?
?6.2 Для ответа на поставленный вопрос обратимся к рассмотрению разности степеней, приведенной к величине
 на основании представления оснований
на основании представления оснований  и
и  через
через  и
и  и использования Бинома Ньютона. [3]
и использования Бинома Ньютона. [3]6.3 Возможность приведения разности степеней к величине
 обеспечивается посредством использования
обеспечивается посредством использования 
.

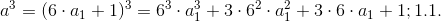
6.4 Определяем разность (1.1.с-1.1.а):
![(c^3-a^3)=6^3\cdot[(c_1)^3-(a_1)^3]+3\cdot 6^2\cdot[(c_1)^2-(a_1)^2]+3\cdot 6\cdot [(c_1)-(a_1)]; 1.1.(с-a)](https://habrastorage.org/getpro/habr/post_images/c4f/0e0/22f/c4f0e022f3024203f0b6b6723d8509a6.gif)
Определяем
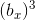
![(c^3-a^3)/[3\cdot 6\cdot (c_1-a_1)]=6\cdot 2\cdot[(c_1)^2+c_1\cdot(a_1)+(a_1)^2]+ 6\cdot [(c_1)+(a_1)]+1=b_x^3; 1.1.к](https://habrastorage.org/getpro/habr/post_images/83f/241/a0a/83f241a0aa25fdfd5b3ff68b80033d6d.gif)
Определяем

![F_{b_{x}^{3}}=(b_{x}^{3}-1)/6=2\cdot[(c_{1})^{2}+c_{1}\cdot a_{1}+ a_{1})^{2}]+[(c_{1})+(a_{1})]; 1.1.к.1](https://habrastorage.org/getpro/habr/post_images/223/2ae/eff/2232aeeff09f111afbbbf7fcc022bc79.gif)
Получаем сумму из двух слагаемых, первое из которых содержит сомножитель
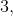 а второе нет.
а второе нет. Это при условии, если сумма
![[(c_1)+(a_1)];](https://habrastorage.org/getpro/habr/post_images/e06/f46/80d/e06f4680d55a59544ff8cadd7de25e98.gif) У.2 сомножителей
У.2 сомножителей 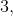 не содержит.
не содержит.В этом случае и величина
 , содержать сомножитель
, содержать сомножитель 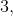 не может.
не может.Для этого варианта всё ясно.
7.1 Как показано ранее, при отсутствии общих сомножителей
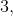 в величинах
в величинах  и
и ,
,невозможно получить точный куб в результате разности
 .
.7.2 Для ответа на вопрос, почему и при наличии общих сомножителей
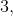 в величинах
в величинах  и
и  невозможно получить в разности кубов точный куб, обратимся к формализованному выражению величины
невозможно получить в разности кубов точный куб, обратимся к формализованному выражению величины 
8.1 Формализованное выражение
 ;
; O.1
O.1Пример расчёта А:

 ;
; 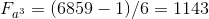 ;
;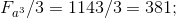
8.2 Определяем

через


8.3 В общем виде:
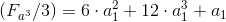 ; У.1
; У.18.4 Откуда точный куб:
 У.2
У.28.5 То есть, по величине

основания

1) Можно рассчитывать точный куб для этого основания.
2) Производить проверку поэтапной делимости величины
 на величину
на величину 
9.1 первый этап деления:

Корректировка:

9.2 Второй этап деления:

Корректировка:

9.3 Третий этап деления:

10.1 Выражение величины
 в формализованном виде У.1 позволяет выражать в аналогичном виде и величину
в формализованном виде У.1 позволяет выражать в аналогичном виде и величину  :
: Z.1
Z.110.2 То есть, посредством деления величины Z.1 на

необходимо получить частное, относящееся к первому классу вычетов по
 .
.11.1 Как отмечалось ранее, деление на

не могут обеспечить принадлежность частного к первому классу вычетов по
 .
.11.2 При этом, в полученном частном останутся, как сомножители, все кубы, введённые в разность
 ,
, относящиеся к первому классу вычетов по
 .
.11.3 При используемом подходе к доказательству БТФ решение сводиться к определению возможности преобразовать

к виду

относящемуся к первому классу вычетов по
 .
.11.4 Но это препятствие не основное.
Основным препятствием является закономерность У.1 и Z.1.
Как отмечалось ранее в

возникают, либо единичные сомножители, равные основаниям степеней, введённых в разность
 , либо не возникают.
, либо не возникают.11.5 Поэтому, целочисленное выражение разности оснований рассматриваемых степеней не может привести к получению целочисленного частного в результате деления Z.1 на

11.6 Поэтому утверждение Большой теоремы Ферма для второго случая, для куба, справедливо, что и требовалось доказать.
12.1 Перейдём к рассмотрению первого случая БТФ для куба.
С этой целью рассмотрим ещё одну найденную закономерность.
При определении
 справедливо:
справедливо:![F_{b_x^n}=(b_x^n-1)/(2n)=[(c^n-a^n)/[n(c-a)]-1]/(2n)$$= [[(c^n-1)/(2\cdot n)-(a^n-1)/(2\cdot n)]/[n\cdot(c_1-a_1)] -1]/(2\cdot 3) ; F_{b_x^n}=(b_x^n-1)/(2n)=\frac{[(c^n-a^n)/(c-a)-1]}{2n}= \frac{[(c^n \pm \Delta_c)/(2n)-( a^n \pm \Delta_a)]/(2n)-(c_1-a_1) }{c-a} ;](https://habrastorage.org/getpro/habr/post_images/da0/826/0d1/da08260d182e2fd35ade19371cd46c0b.gif)
12.2 А, именно.
![F_{b_x^n}=(b_x^n-1)/(2n)=\frac{[(c^n-a^n)/(c-a)-1]}{2n}= \frac{[(c^n \pm \Delta_c)/(2n)-( a^n \pm \Delta_a)]/(2n)-(c_1-a_1) }{c-a}ж](https://habrastorage.org/getpro/habr/post_images/790/a27/cdb/790a27cdb8b9f53f6ff59166405de8f6.gif)
Необходимость корректировки

объясняется разностью количества величин
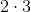 , принятых к расчёту.
, принятых к расчёту.12.3 Это позволяет приравнять рассмотрение второго и первого случаев, так как нахождение разности степеней и для первого случая БТФ приводит к аналогичному варианту, тождественному второму случаю БТФ.
Поэтому можно заметить, что утверждение Большой теоремы Ферма справедливо, как для второго случая, так и для первого случаев при рассмотрении куба.
Что и требовалось доказать.
Литература:
1. Г.Эдвардс «Последняя теорема Ферма».
2. М.М. Постников «Введение в теорию алгебраических чисел».
3. М.Я. Выгодский «Справочник по элементарной математике».
Комментарии (48)

Refridgerator
07.10.2016 16:44+1Чем ваше доказательство лучше, например, вот этого?

Iosif1
07.10.2016 17:23-2Доказательство должно быть доказательством.
Если оно доказательство, то оно, уже класс.
Помнится Марк Твен написал самый короткий рассказ, и получил премию:
«Джо сидел на бочке из-под бензина, закуривая. Покойному было двадцать четыре года.»
У Вас доказательство, по моему, короче.
Я могу ещё короче: «Этого не может быть, потому что не может быть никогда!»

Iosif1
08.10.2016 19:44-1Refridgerator, Если я Вас обидел, то примите мои извинения.
Хочу Вас спросить: " Вы, серьёзно, считаете доказательством Большой теоремы Ферма, написанное по ссылке, вами указанной?"
Refridgerator
08.10.2016 20:19+1Конечно нет, обижаться мне совершенно не на что.
Я думаю, что единственным доказательством Теоремы Ферма является доказательство Эндрю Уайлса. А все остальные — это не доказательства, а такой хитрый способ самоутвердится и почувствовать себя умнее всех других. Автор по ссылке, точно также как и вы, просто в какой-то момент поверил, что он это доказательство нашёл.
Iosif1
08.10.2016 20:58-1Уважаемый Refridgerator, доказательство Эндрю Уайлса принимаете на веру, или Вы до конца в теме?
Я к чему, если второе, то у меня просьба, подскажите, пожалуйста, где в моём доказательстве ляпсус.
Уделите внимание, предлагаемое доказательство, несомненно, проще, чем доказательство Эндрю Уайлса.
С вопросами, Вы за час разберётесь.
Ну, может быть, я немного преувеличиваю.
Мне кажется, что это и Вам может быть интересно.
Если нет ляпсуса, то любая степень доказывается аналогично.
Поверьте мне, что я показал доказательство, только потому, что не вижу в нём изъянов.
Кроме изложения доказательства, но я старался.
Благодарен, что не таите зла.
Refridgerator
08.10.2016 22:34+1Ляпсус вашего доказательства в том, что оно отсутствует. Как минимум потому, что никакое доказательство не может считаться доказательством, пока его истинность не подтвердят другие математики. У того же Уайлса первоначальную версию доказательства не приняли, потому что оно оказалось недостаточно строгим, и он потом его ещё год дорабатывал.
Предположим, что существует более простое доказательство, чем с привлечением эллиптических кривых. Почему же за 300 лет никто из величайших математиков не смог его обнаружить? Те самые, которую эту математику и построили. Вероятно потому, что такого доказательства быть не может, либо же нет ещё инструментов, с помощью которых такое доказательство можно построить.
Ваш текст не является доказательством, потому что в нём нет логической связи между фразами. Некоторые фразы повторяются по два раза, например:
1.2 Выразим основания равенства 1.1 через единые аргументы, для чего вводим следующие обозначения:
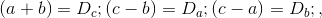
где, например,
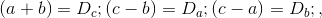
Там также присутствуют лишние символы (запятая в конце здесь, вопросы и точки в других формулах). И если вы в упор не видите столь очевидные ошибки, это может значить только одно — критическое мышление у вас отсутствует и вы вообще не способны распознавать ошибки, ни свои, ни чужие. Что также продемонстрировали чуть ранее на моё предложение сравнить своё доказательство с другим.
Iosif1
08.10.2016 23:16-1Уважаемый Refridgerator, спасибо за замечания. Постараюсь исправить.
Что касается вопросительных знаков, проставил умышленно.
Не подумал, что будет воспринято как ошибка.
Насчёт сравнения доказательств — воспринял, априори, как критику без разбора.
Доброй ночи.

Iosif1
07.10.2016 17:30-4Минусы уже пошли, по каким причинам — не ведомо. Неужели так быстро соображаете?
А чего, тогда Вы не доказали до сих пор теорему сами?
Вопрос очень интересный. Не правда, ли, господа, «минуссоеды».
Refridgerator
07.10.2016 18:09+2Зачем доказывать то, что уже доказано? Есть и другие открытые математические проблемы.

Iosif1
07.10.2016 18:13-4Отвечу на Ваш вопрос, если Вы ответите на мой: Вы мне минус фуга нули?

Refridgerator
07.10.2016 18:28+1Это был не вопрос, а ответ.

Iosif1
07.10.2016 18:38-6Я Вам до вашего, так называемого ответа, вопросов не задавал, господин «карма пожиратель».
К рысак, отъедает яйца у мужиков в крысином помёте, всё хочет сам, как и «карма пожиратели».
Учуяли сходство?
Refridgerator
07.10.2016 18:51+3Вы написали:
Хочется услышать мнение
Если было бы «Хочется услышать положительное мнение», возможно, была бы другая реакция.

Iosif1
08.10.2016 19:37-1Уважаемый ads83, я не одобрил вашу просьбу.
Хочу объяснить, почему.
Вы хотите, чтобы было рассмотрено равенство с тремя нечётными основаниями.
Это не требует рассмотрения, так как такое равенство априори существовать не может.
Мне наставляют минусов без всякого объяснения.
А я жажду объяснений, если я не прав, подскажите мне, где, и в чём.
Я не против того, чтобы, по возможности, соблюдать режим, заданный условиями.
Но определить условия без разъяснений не всегда легко.
Поэтому я объясняю отклонения вашей просьбы.
ads83
08.10.2016 22:48Спасибо за ответ, действительно ошибся.
Чтобы ваши ответы не выглядели «разговором с воображаемым собеседником», пожалуйста одобряйте в том числе ошибочные предположения. Тогда будет диалог :)
Для меня и для вас ответ понятен. Для всех остальных — нет.
Возвращаясь к сути моего вопроса. Давайте рассмотрим пример 7^3+11^3=c^3 и, следуя вашему доказательству, убедимся что с не может быть целым числом
Я хочу разобраться в доказательстве, но не все понятно. Анализируя частный случай, двигаясь от простого к сложному, разложим все по полочкам
Iosif1
09.10.2016 07:51-1Уважаемый ads83.
Я всё таки постараюсь ответить на ваш вопрос относительно рассмотрения примера
7^3+11^3=c^3;
Если я вас правильно понял, Вы хотите, чтобы было показано доказательство для первого случая БТФ, для суммы степеней, а не для разности, при условии, когда a и b — нечётные?
Если Вы заметили в рассматриваемом доказательстве обязательным условием является условие, когда разности оснований в разности степеней обеспечивают точный куб.
Это условие обязательное и для рассмотрения суммы степеней. В этом случае, сумма оснований степеней (a+b) в сумме степеней должны обеспечивать точный куб. Поэтому предлагаемые величины оснований a и b не корректные.
Это не означает, что предлагаемое доказательство рассматривает не все возможные варианты.
Это требование условия теоремы, так как (a+b) и (a*a+a*b+b*b), как сомножители, на которые разлагается сумма кубов, обязательно, взаимно простые числа.
Исключение, когда a и b содержат общие сомножители, тоже, нарушают условия теоремы, так как основания a, b и с не должны иметь общих сомножителей.
ads83
09.10.2016 10:23+1А вот это как раз вопрос к вам, как к автору: в какой случай попадает мой пример? Я хочу понять, разобраны ли в доказательстве все возможные случаи для любых натуральных чисел.
Понимаете, доказательство обязано содержать четкое описание области применимости и внутри себя показывать, что рассмотрено всё. Доказательство всёшности порой может занимать многие страницы :) Причем в строгом доказательстве словосочетания «аналогично доказывается» заменяются на эти самые аналогичные рассуждения.
В преамбуле я увидел, что вы ставите одно ограничение: в уравнении a^n+b^n=c^n рассматриваются случаи, когда n=3. Таким образом, мой пример рассматривается в каком-то из пунктов вашего доказательства. В каком?
Iosif1
09.10.2016 13:33-1Да, изложение доказательства не совершенно, я не имею специального математического образования.
Да у меня с юности изложение не является козырем.
Но, доказательство «всёшности» существует в источниках, указанных в теме.
На Математическом форуме МГУ dxdy в разделе «Великая теорема Ферма» есть тема в которой заслуженный участник, с логином swedka, даёт ссылки на источники, в которых рассматриваются возможные варианты, уже доказанные.
Ваш вариант тоже где то упоминается.
Не доказанным остаётся только тот, который рассматривается в теме.
Об этом указано.
Можно сказать, что истинность рассмотренного варианта завершает доказательство БТФ, при этом, с использованием приёмов элементарной математики.
Кстати, доказательство Эндрю Уайлса, не охватывает рассмотрение куба.
И, может быть поэтому на форуме dxdy требуют доказательство для куба.
То есть, доказательство для куба приёмами элементарной математики остаётся актуальным.
По аналогии, на основании используемой методики доказательства, БТФ доказывается для любой степени.
Ваши вопросы вселяют уверенность в вашем профессионализме, но написать всеобъемлющий труд мне не по возможности.
Мне кажется, что Вы в этом уже убедились.
ads83
09.10.2016 22:00+1Тогда вам стоит уточнить формулировку: с Я привожу доказательство БТФ для n=3 на Доказательство БТФ для частного случая и в первом же абзаце указать рамки применимости, со ссылками и объяснениями. По возможности — чем эта частная проблема замечательна
У вас в голове загружен контекст, т.е. источники, доказательства других вариантов, перечень всех вариантов, ссылки и сноски. Для неподготовленного же читателя (в том числе меня) ваша статья начинается с середины: что за основания, обеспечивающие 2 Случай БТФ? Возможно, поэтому статью и заминусовали.
Сам по себе рассказ о том, какие случаи уже доказаны с использованием «простой» математики, какие остались и какие сложности на этом пути у сообщества — уже может потянуть на статью. Уверен, при последовательном изложении она вызовет интерес на Хабре.
Iosif1
09.10.2016 23:16-2Спасибо за вселение надежды.
Однако доказательство рассчитано на подготовленного читателя, знакомого с проблемой.
У меня не было и нет желание объяснить всю историю.
Это сделано другими, в разной степени талантливости и доходчивости.
Я дал ссылки на литературу, которая мне помогла разобраться в проблеме.
Хочу отметить, что и ныне математическая общественность по разному трактует условия теоремы.
Я не до конца понимаю предмет спора. И не стараюсь, принимая те условия, которые показаны в работе.
Для неподготовленного читателя доказательство Большой теоремы Ферма не может вызвать интерес в оценке истинности доказательства.
Поэтому я предпочитаю называть теорему Большой, а не Великой
О её величии, верно, не мне судить.
А вот то, что она большая — спора не вызывает.
И нужен не дюжий талант, чтобы только попытаться осветить весь материал.
У меня его нет.
Скажу также, что, по моему мнению, даже математики, используемые различные подходы для решения, не всегда легко понимают друг друга.
Многие читают ради любопытства, а не ради любознательности.
А некоторые, чтобы расставлять минусы.
Бог им судья.
Но, за рекомендации благодарен.

Refridgerator
10.10.2016 05:49+1Теорема Ферма «Большая», потому что ещё есть и Малая теорема Ферма.

Iosif1
10.10.2016 11:23-1Спасибо за напоминание.
Если бы Вы читали доказательство, то бы заметили, что я на неё, эту теорему, ссылаюсь.
А написал я о том, что предпочитаю называть теорему Ферма Большой, потому, что, мне указал bromzh в теме " Доказательство второго случая...", что правильно называть Большую теорему Ферма Великой.
Вот такие пироги.
Refridgerator
10.10.2016 12:31+1Более того, я даже сходил на dxdy, где оказался целый раздел, посвящённый ферматистам. Как Вы и указалали, там Вам задавали (вполне здравые) вопросы, не на все из которых Вы предоставили ответы, так же, как и ушли от ответа и на мой вопрос. Кроме того, там обнаружилось множество и других доказательств, в том числе и для частных случаев, и вопрос корректности всех этих доказательств по-прежнему остаётся открытым.
(И к слову, алгебра вычетов к элементарной математике всё-таки не относится).
Iosif1
10.10.2016 13:14-1Как же так, там читали, а мою работу не читали.
На какой это ваш вопрос я не ответил?
На этот: «Чем отличается моё доказательство от того, на которое вы дали ссылку?»
А как на него надо ответить?
— Надеюсь, что всем.
Если желаете, я Вам напишу, почему доказательство по ссылке не корректно?
Правда вы сказали, что вы это знаете.
Вы хотите проверить, понимаю ли я, то, что понимаете Вы?
Наверное, не всё.
Неужели вы считаете, что человек, что то доказавший должен знать все ошибочные попытки доказательства того, что он доказал.
Я так не считаю.
Но ошибку в доказательстве, на которое вы дали ссылку, я объясню, если Вы пожелаете.
Насчёт того, что алгебра вычетов не относится к элементарной математике, я могу согласиться, так как действительно это не предусматривалось в школьной программе, когда я был школьником.
Но, когда сын был школьником, то в школьной программе уже изучали производные и интегралы.
Что это тоже разделы элементарной математики.
Я так не считаю. Да ещё множества, о которых нам школярам не докладывали, и которые, по моему мнению исказили воспитание логического мышления.
Что в статье, по вашей ссылке, неоспоримо, так это формулировка, что элементарная математика — «несколько неопределённое понятие».
И, просьба, напишите на какие вопросы я не ответил, или ответил глупо, мне это очень интересно. Может быть, это на те, на которые мне не дали ответить, закрыв тему.
То что показал, последнее, на Хабрахабре на dxdy в закрытой теме " Доказательство первого случая БТФ".
На Хабрахабре легче использовать теги.
А это для меня, очень, не мало важно.
Воспользуюсь случаем, и поблагодарю администрацию Хабрахабра, что мне, уже с отрицательной кармой, по моей просьбе, обеспечили карму +1, что позволило пользоваться тегами.
Ныне, как Вы понимаете, я лишён возможности показывать доказательство БТФ для любых степеней.
Как любил говорить один мой собеседник «Не всё коту масленица!»

Iosif1
08.10.2016 22:56-1Уважаемый ads83.
Я, как имеющий отрицательную карму, не могу пользоваться тегами.
Поэтому, просьба:
Задавайте конкретный вопрос по материалу.
Слева нумерация, чтобы легче искать.
Могу предложить беседы по Skype: Iosif 705, так как там можно показывать экран.

nikolay_karelin
09.10.2016 21:05+1А почему не в математический журнал? Или хотя бы на arXiv.org + researchgate — на последнем можно в принципе получить профессиональную рецензию…
Кстати, а почему нет ссылок на оригинальные статьи по теме?
И большое спасибо за ссылку на книгу Эдвардса! Я в свое время с большим удовольствием читал книжку Саймона Сингха, про современное доказательство теоремы.
Iosif1
09.10.2016 21:55-1А Вам большое спасибо за весточку. И за советы.
К сожалению, я человек не подготовленный к оформлению работы для публикации в математическом журнале.
Даже не знаю, какие можно использовать теги.
Так получилось, что я в одиночестве, без возможности получить нужные рекомендации.
Если Вас не затруднит, я поспрашиваю Вас о готовности материала для математического журнала.
С удовольствием бы воспользовался сотрудничеством с Вами.
Соавторство с Вами было бы самым большим призом от общения на Хабрахабре.
Поищу книгу Саймона Сингха в интернете.
Надеюсь с Вами у слышаться.
Ещё раз спасибо за весточку.
nikolay_karelin
10.10.2016 21:41+1Вынужден отказаться. Я занимаюсь совершенно другими вещами, и если про Ферма читал популярные вещи (или учебники), то это не значит, что полезу в эту тему.
За прошедшие столетия было сломано столько копий, что сделать что-то оригинальное будет слишком сложно: потребуется прочитать под карандаш
сотнитысячи статей и со всеми разобраться (только на статью Уайлса, где приведено современное доказательство, Google Scholar дает 2000 с лишним ссылок, а всего по запросу "last Fermat theorem" — 31 000 с чем-то).
Лезть в эту тему, не работая в приличном математическом институте с давней традицией исследования по теории чисел — форменное безрассудство...
То есть, конечно, лестно было бы найти именно оригинальное доказательство Ферма, но я уж лучше займусь чем-нибудь более реалистичным ;)
Тем более, что вполне возможно, что "последняя теорема" — гениальная ошибка.

Iosif1
10.10.2016 22:00-1Ваше решение для меня не в удовольствие, но вполне реалистичное.
Действительно, «лезть в эту тему» можно только с убеждением в истинности найденного доказательства.
Я не понял, почему Вы считаете, что «последняя теорема» может быть гениальной ошибкой, и какое значение имеет количество ссылок, которое даёт Google Scholar.
Я считаю, что все авансируемые ссылками материалы к найденному доказательству никакого отношения не имеют.
Но это уже не важно.
За ответ спасибо.
Успехов в чём то более реалистичном.
nikolay_karelin
11.10.2016 13:30+1Про гениальную ошибку: это было высказано в книге Саймона Сингха. Идея в том, что есть вероятность, что у самого Ферма доказательство содержало ошибку, но он ее не заметил, а поиски элементарного доказательства теоремы обречены на неудачу.
Мне эта идея близка: публиковать такие вещи надо с самого начала!
Про число ссылок: последняя теорема Ферма — одна из самых популярных математических загадок последних трехсот лет. Ею занималась толпа не самых глупых людей на протяжении всего становления современной науки. Например, первым доказательство для тройки предложил Эйлер. Естественно, самый первый вопрос любого вашего оппонента — как ваше доказательство соотносится с другими. Например оно может быть проще для понимания, приводить к интересным следствиям, может что-то еще.
И, поскольку научные публикации — это основной метод общения в научном сообществе, если в статье нету ссылок на основные относящиеся к делу публикации, и их критический анализа (и на этапе постановки задачи, и обсуждения результата), то такое доказательство действительно никто читать не будет, и в печать не примут.
С другой стороны, возможно ваше доказательство уже кто-то предлагал, и в нем был не замеченные вами ошибки.
Поэтому, без знания литературы в какую-то область науки лезть без толку. Говорю это со всей уверенностью, ибо в своей области (оптика, лазерная физика и рядом), я работал в нескольких направлениях, и небезуспешно.
И наконец: раз доказательство Уайлса за 10 с лишним лет никто не опроверг, и в этом году ему присуждена Абелевская премия, то мне проще считать его истинным. Оно конечно, очень сложное, но насколько я понимаю, рецензировали его весьма и весьма внимательно.

Iosif1
11.10.2016 16:26-1Книгу Саймона Сингха нашёл только на английском языке. Не владею.
«есть вероятность, что у самого Ферма доказательство содержало ошибку, но он ее не заметил, а поиски элементарного доказательства теоремы обречены на неудачу»
С первым утверждением полностью согласен, со вторым — нет.
Замечу, что даже Ньютон высоко оценил труды Пьера Ферма, сказав, что без трудов Пьера Ферма, ему вряд ли бы удалось сделать свои открытия.
Не знаю, имел ли он ввиду Большую теорему.
Выше похвалы, по моему мнению, быть не может.
«Да куда же Вы, тогда, лезете?», скажет любой, относительно меня.
Дело в том, что Ферма не имел современных расчётных программ, которые и позволили мне найти закономерности, до селе неизвестные.
Могу объяснить более конкретно. Но, это при желании.
Меня, вообще удивляет, как с «теми» вычислительными устройствами, Пьеру Ферма удалось так многое.
Не даром Ньютон сказал:
«Я стоял на головах гигантов», имея ввиду, верно, и голову Пьера Ферма.
«Мне эта идея близка: публиковать такие вещи надо с самого начала!»
Это я почувствовал, и понял, что Вы человек подготовленный очень, очень.
Этим талантом я, почему то, обладаю.
Поэтому я к Вам и обратился с предложением, быть соавтором.
И насчёт ссылок Вы правы.
Конечно, необходим «патентный» поиск, если есть сомнения.
Иван Павлов говорил:
«Ничего не принимайте на веру, всё подвергайте сомнению».
Но я уверяю Вас, что аналогичного подхода к доказательству Большой теоремы Ферма, не существует.
Это, даже видно, по реакции оппонентов.
Если они видят какой то ляпсус, они одни, а если не видят, начинаются вы каблучки.
Поэтому, утверждаю, что не возможно что «доказательство уже кто-то предлагал, и в нем были не замеченные ошибки».
Но убеждаться в этом надо, конечно, лично.
Каким образом, каким путём? Анализом ли всего наделанного, или при помощи проверки метода?
Я бы предпочёл второй путь.
Мне интересней рождение вывода, чем его изучение.
Поэтому, что касается Большой теоремы Ферма, с ссылками, всё сложней, и всё проще. Есть несколько источников, отвечающие на многое, сразу.
И, наконец.
Что касается доказательство Уайлса, в котором я ничего не понимаю, то мне известно, что его доказательство, почему то, не обеспечивает доказательство для третьей степени. Поэтому, доказательство, даже, только для третьей степени актуально.
Вероятнее всего, это связано с гипотезой Била.
Считают, что если Большая теорема Ферма будет доказана до конца, то, автоматически, будет доказана и гипотеза Била.
На что я не имею окончательного мнения.

Refridgerator
12.10.2016 07:33+1Книгу Саймона Сингха нашёл только на английском языке.
Эта книга есть в русском переводе.
Если вы не можете найти то, что есть, то как же вам тогда удалось найти то, чего нет? (извините, не удержался)
Iosif1
12.10.2016 09:36-1Извиняю. В Интернете?
На ваше замечание могу только заметить, что Поиск и нахождение доказательства — это, по моему мнению, не идентичные способности.
Многим композиторам можно сказать: " Как вы могли написать хорошую музыку, если вы не умеете петь!"
nikolay_karelin
12.10.2016 21:30+2Книжка на русском гуглится сразу ;)
Кстати, без английского языка (а в случае Ферма стоило бы еще знать французский, немецкий, скорее всего латынь) вы далеко в науке не уедете.

Iosif1
12.10.2016 22:04-1А у меня сразу не гуглится.
Но я от этого не в печали.
Сказанное вами о невозможности мне уехать далеко без английского — истина.
Это грустная истина!
Поэтому мне многие необходимые действия оказались не доступны.
Правда, я уже давно, это понял.
Помогло бы мне хоть куда то уехать в науке, и со знанием английского, вопрос останется открытым.
Меня интересует только ответ на вопрос:
Удастся ли мне узнать мнение о работе специалистов, находящихся в теме, не по существовавшим попыткам, а, непосредственно, по показанной работе.
Надежды нечтожны.

Refridgerator
12.10.2016 08:18+1А ещё вот в этой статье 10-летней давности говорится, что более простого доказательства быть не может (и объясняется, почему).

Iosif1
12.10.2016 09:29-1Спасибо, Статья интересная. Вы очень стоящий оппонент.
Дмитрий Абрамов пишет:
«Осталось доказательство только понять».
Доказательство построено на основе эллиптических кривых по гипотезе
Таниямы–Шимуры-Вейля, доказанной частично.
Несомненно, это всё плод больших умов.
Но, мнение автора о невозможности доказательства Большой теоремы Ферма можно оспорить.
Описывается такое событие:
Когда выбрали место для строительства Исаакиевского собора, возникла необходимость убрать огромный валун, находящейся, как раз, на этом месте.
Его бурили, взрывали, разогревали кострами, обливая потом водой — ничего не помогало.
Собрался консилиум больших учёных, чтобы решить поставленную задачу.
Ходят, мудрствуют.
И, вдруг, какой то проходящий мужик говорит:
«А вы яму выройте».
Вырыли яму, и не каких проблем.
Может быть, и с Большой теоремой Ферма также.
Помните, крылатое: «А ларчик просто открывался».
В зависимости от выбранной методики очень зависит и продолжительность пути к доказательству, и его успех.
Ещё раз спасибо за статью, но вы в доказательстве найдите изъян.
Доказательство перед вами. Его, даже искать не надо.

Iosif1
10.10.2016 16:23-1Чтобы я не написал, всё принимается на «Ура!»
Как в том анекдоте: «На карабу! На карабу!»
Вынужден за это поблагодарить.
Refridgerator
10.10.2016 18:20+1Минусы возле ваших комментариев означают лишь, что количество проголосовавших «вниз» на единицу больше, чем проголосовавших «вверх». Возможно, это ваши конкуренты с dxdy.ru стараются. Поэтому если Вас смущает отрицательная суммарная оценка — опубликуйтесь на ресурсе, где возможность комментирования отсутствует, как это сделал, например, Перельман с доказательством гипотезы Пуанкаре.

Iosif1
10.10.2016 19:27-1Спасибо за совет.
Я бы с удовольствием ему последовал, но не знаю, как это сделать.
Меня не отрицательная карма смущает, а неопределённость.
Помните в фильме: «Иван Васильевич меняет профессию», герой, которого играет замечательный артист Леонид Куравлёв, говорит: «Это я хорошо зашёл».
А я думаю: «Туда ли я зашёл».
Вам спасибо, что уделяете мне внимания, хотя мы и говорим на разных языках. Как то так получается.
Подскажите, если не трудно, как можно выполнить Ваш совет, при условии, что английским, я не владею.
Заранее благодарен.


jbubsk
Как говорил мой препод — «Что вам не понятно? Вот альфа, вот омега».
Iosif1
Непонятно многое.
Подскажите, например, почему у меня не получается попытка спрятать часть изложения?
Делаю всё по инструкции. Как то раньше получилось.
Если не трудно.
Ramires
Хабракат у вас работает. Или Вы о чём-то другом?
Iosif1
А что такое Хабракат?
Вписываю текст, по инструкции и не хрена.