Python обладает рядом привлекательных преимуществ к которым относится простота реализации программных решений, наглядность и лаконичность кода, наличие большого числа библиотек и многочисленного активного комьюнити. В то же время, известная всем медлительность питона часто ограничивает его применимость для “тяжелых” вычислений. Для ряда задач можно добиться существенного ускорения расчетов путем использования технологии CUDA для параллельных вычислений на GPU. Цель этого небольшого исследования — анализ возможностей эффективного использования python для расчетов на GPU и сравнение производительности различных python-решений с реализацией на C.
Введение
По роду деятельности я частенько занимаюсь задачами численного моделирования. Во многих случаях мы используем технологию CUDA для ускорения расчетов за счет использования возможностей параллельных вычислений на GPU, при этом программы пишутся на языке C. В то же время, в некоторых случаях хотелось бы иметь возможность реализовывать расчеты на питоне, потому что это удобно, быстро, гибко, лаконично,
Тестовая задача
Выбор тестовой задачи и условий тестирования был обусловлен характером реальных задач, для решения которых в дальнейшем планируется использование python. При этом была выбрана максимально простая задача, а именно задача решения двумерного уравнения теплопроводности с помощью явной конечно-разностной схемы. Задача рассматривалась на квадратной области с заданными значениями температуры на границах. Количество узлов расчетной сетки по x и y одинаково и равно n. На рисунке в начале статьи показано установившееся решение тестовой задачи.
Алгоритм и условия тестирования
Алгоритм решения задачи можно представить следующим псевдокодом:
Инициализировать массивы u0 и u, хранящие значения решения на текущем и следующем временном шаге
включить таймер
выделить память на девайсе и скопировать массивы u0 и u с хоста на девайс
for(i = 0; i < nstp/2; i++)
вычислить значение u на следующем шаге по времени, зная значение u0 на текущем временном шаге
вычислить значение u0 на следующем шаге по времени, зная значение u на текущем временном шаге
скопировать результат (u0) с девайса на хост
выключить таймер и вывести результатВо всех тестах представленных ниже число узлов квадратной сетки в каждом направлении (n) варьировалось от 512 до 4096, а nstp = 5000.
Программное и аппаратное обеспечение
Тестирование проводилось на персональном компьютере:
Intel® Core(TM)2 Quad CPU Q9650 @ 3.00GHz, 8 Gb ОЗУ
GPU: Nvidia GTX 580
Операционная система: Ubuntu 16.04 LTS с установленной CUDA 7.5
Реализация на C
Все дальнейшие python-реализации сравнивались с результатами, полученными с помощью программы на C, описанной в этом разделе.
#include <stdio.h>
#include <time.h>
#include <cuda_runtime.h>
#define BLOCK_SIZE 16
int N = 512; //1024; //2048;
double L = 1.0;
double h = L/N;
double h2 = h*h;
double tau = 0.1*h2;
double th2 = tau/h2;
int nstp = 5000;
__constant__ int dN;
__constant__ double dth2;
__global__ void NextStpGPU(double *u0, double *u)
{
int i = blockDim.x * blockIdx.x + threadIdx.x;
int j = blockDim.y * blockIdx.y + threadIdx.y;
double uim1, uip1, ujm1, ujp1, u00, d2x, d2y;
if (i > 0)
uim1 = u0[(i - 1) + dN*j];
else
uim1 = 0.0;
if (i < dN - 1)
uip1 = u0[(i + 1) + dN*j];
else
uip1 = 0.0;
if (j > 0)
ujm1 = u0[i + dN*(j - 1)];
else
ujm1 = 0.0;
if (j < dN - 1)
ujp1 = u0[i + dN*(j + 1)];
else
ujp1 = 1.0;
u00 = u0[i + dN*j];
d2x = (uim1 - 2.0*u00 + uip1);
d2y = (ujm1 - 2.0*u00 + ujp1);
u[i + dN*j] = u00 + dth2*(d2x + d2y);
}
int main(void)
{
size_t size = N * N * sizeof(double);
double pStart, pEnd, pD;
int i;
double *h_u0 = (double *)malloc(size);
double *h_u1 = (double *)malloc(size);
for (i = 0; i < N*N; ++i)
{
h_u0[i] = 0.0;
h_u1[i] = 0.0;
}
pStart = (double) clock();
double *d_u0 = NULL;
cudaMalloc((void **)&d_u0, size);
double *d_u1 = NULL;
cudaMalloc((void **)&d_u1, size);
cudaMemcpy(d_u0, h_u0, size, cudaMemcpyHostToDevice);
cudaMemcpy(d_u1, h_u1, size, cudaMemcpyHostToDevice);
cudaMemcpyToSymbol(dN, &N, sizeof(int));
cudaMemcpyToSymbol(dth2, &th2, sizeof(double));
dim3 dimBlock(BLOCK_SIZE, BLOCK_SIZE, 1);
dim3 dimGrid(N/BLOCK_SIZE, N/BLOCK_SIZE, 1);
for(i = 0; i < int(nstp/2); i++)
{
NextStpGPU<<<dimGrid,dimBlock>>>(d_u0, d_u1);
NextStpGPU<<<dimGrid,dimBlock>>>(d_u1, d_u0);
}
cudaMemcpy(h_u0, d_u0, size, cudaMemcpyDeviceToHost);
cudaFree(d_u0);
cudaFree(d_u1);
pEnd = (double) clock();
pD = (pEnd-pStart)/CLOCKS_PER_SEC;
printf("Calculation time on GPU = %f sec\n", pD);
}
free(h_u0);
free(h_u1);
return 0;
}
Расчеты показывают, что для N = 512 время выполнения C-программы распараллеленной на GPU составляет 0.27 секунд против 33.06 секунд для последовательной реализации алгоритма на CPU. То есть ускорение CPU/GPU составляет около 120 раз. С ростом N величина ускорения не убывает.
Python with Numba
Библиотека Numba предоставляет возможность jit (just-in-time) компиляции кода на питоне в байт-код сравнимый по производительности с C или Fortran кодом. Numba поддерживает компиляцию и запуск python-кода не только на CPU, но и на GPU, при этом стиль и вид программы, использующей библиотеку Numba, остается чисто питоновским.
from numba import cuda
import numpy as np
import matplotlib.pyplot as plt
from time import time
n = 512
blockdim = 16, 16
griddim = int(n/blockdim[0]), int(n/blockdim[1])
L = 1.
h = L/n
dt = 0.1*h**2
nstp = 5000
@cuda.jit("void(float64[:,:], float64[:,:])")
def nextstp_gpu(u0, u):
i,j = cuda.grid(2)
if i > 0:
uim1 = u0[i-1,j]
else:
uim1 = 0.
if i < n-1:
uip1 = u0[i+1,j]
else:
uip1 = 0.
if j > 0:
ujm1 = u0[i,j-1]
else:
ujm1 = 0.
if j < n-1:
ujp1 = u0[i,j+1]
else:
ujp1 = 1.
d2x = (uim1 - 2.*u0[i,j] + uip1)
d2y = (ujm1 - 2.*u0[i,j] + ujp1)
u[i,j] = u0[i,j] + (dt/h**2)*(d2x + d2y)
u0 = np.full((n,n), 0., dtype = np.float64)
u = np.full((n,n), 0., dtype = np.float64)
st = time()
d_u0 = cuda.to_device(u0)
d_u = cuda.to_device(u)
for i in xrange(0, int(nstp/2)):
nextstp_gpu[griddim,blockdim](d_u0, d_u)
nextstp_gpu[griddim,blockdim](d_u, d_u0)
cuda.synchronize()
u0 = d_u0.copy_to_host()
print 'time on GPU = ', time() - st
Отметим тут несколько приятных особенностей. Во-первых, эта реализация намного короче и нагляднее. Здесь мы использовали двумерные массивы, что делает код намного более удобочитаемым. Во-вторых, если в C-реализации от нас требовалось передать все константы (например N) путем исполнения функций вроде
cudaMemcpyToSymbol(dN, &N, sizeof(int)); то здесь мы просто пользуемся глобальными переменными как в обычной python-функции. Ну и наконец, реализация не требует никаких знаний языка C и архитектуры GPU.Этот код легко переписать и для случая использования одномерных массивов размера n*n, как будет показано далее это существенно влияет на скорость выполнения.
from numba import cuda
import numpy as np
import matplotlib.pyplot as plt
from time import time
n = 512
blockdim = 16, 16
griddim = int(n/blockdim[0]), int(n/blockdim[1])
L = 1.
h = L/n
dt = 0.1*h**2
nstp = 5000
@cuda.jit("void(float64[:], float64[:])")
def nextstp_gpu(u0, u):
i,j = cuda.grid(2)
u00 = u0[i + n*j]
if i > 0:
uim1 = u0[i-1 + n*j]
else:
uim1 = 0.
if i < n-1:
uip1 = u0[i+1 + n*j]
else:
uip1 = 0.
if j > 0:
ujm1 = u0[i + n*(j-1)]
else:
ujm1 = 0.
if j < n-1:
ujp1 = u0[i + n*(j+1)]
else:
ujp1 = 1.
d2x = (uim1 - 2.*u00 + uip1)
d2y = (ujm1 - 2.*u00 + ujp1)
u[i + n*j] = u00 + (dt/h/h)*(d2x + d2y)
u0 = np.full(n*n, 0., dtype = np.float64)
u = np.full(n*n, 0., dtype = np.float64)
st = time()
d_u0 = cuda.to_device(u0)
d_u = cuda.to_device(u)
for i in xrange(0, int(nstp/2)):
nextstp_gpu[griddim,blockdim](d_u0, d_u)
nextstp_gpu[griddim,blockdim](d_u, d_u0)
cuda.synchronize()
u0 = d_u0.copy_to_host()
print 'time on GPU = ', time() - st
PyCUDA
Второй из протестированных python-библиотек была библиотека PyCUDA. В отличии от Numba здесь от разработчика потребуется написать код ядра на C, поэтому без знания этого языка не обойтись. С другой стороны кроме собственно ядра на C ничего писать не надо.
import pycuda.driver as cuda
import pycuda.autoinit
from pycuda.compiler import SourceModule
import numpy as np
import matplotlib.pyplot as plt
from time import time
n = 512
blockdim = 16, 16
griddim = int(n/blockdim[0]), int(n/blockdim[1])
L = 1.
h = L/n
dt = 0.1*h**2
nstp = 5000
mod = SourceModule("""
__global__ void NextStpGPU(int* dN, double* dth2, double *u0, double *u)
{
int i = blockDim.x * blockIdx.x + threadIdx.x;
int j = blockDim.y * blockIdx.y + threadIdx.y;
double uim1, uip1, ujm1, ujp1, u00, d2x, d2y;
uim1 = exp(-10.0);
if (i > 0)
uim1 = u0[(i - 1) + dN[0]*j];
else
uim1 = 0.0;
if (i < dN[0] - 1)
uip1 = u0[(i + 1) + dN[0]*j];
else
uip1 = 0.0;
if (j > 0)
ujm1 = u0[i + dN[0]*(j - 1)];
else
ujm1 = 0.0;
if (j < dN[0] - 1)
ujp1 = u0[i + dN[0]*(j + 1)];
else
ujp1 = 1.0;
u00 = u0[i + dN[0]*j];
d2x = (uim1 - 2.0*u00 + uip1);
d2y = (ujm1 - 2.0*u00 + ujp1);
u[i + dN[0]*j] = u00 + dth2[0]*(d2x + d2y);
}
""")
u0 = np.full(n*n, 0., dtype = np.float64)
u = np.full(n*n, 0., dtype = np.float64)
nn = np.full(1, n, dtype = np.int64)
th2 = np.full(1, dt/h/h, dtype = np.float64)
st = time()
u0_gpu = cuda.to_device(u0)
u_gpu = cuda.to_device(u)
n_gpu = cuda.to_device(nn)
th2_gpu = cuda.to_device(th2)
func = mod.get_function("NextStpGPU")
for i in xrange(0, int(nstp/2)):
func(n_gpu, th2_gpu, u0_gpu, u_gpu,
block=(blockdim[0],blockdim[1],1),grid=(griddim[0],griddim[1],1))
func(n_gpu, th2_gpu, u_gpu, u0_gpu,
block=(blockdim[0],blockdim[1],1),grid=(griddim[0],griddim[1],1))
u0 = cuda.from_device_like(u0_gpu, u0)
print 'time on GPU = ', time() - st
Выглядит это все как чистый питон за исключением локальной вставки C-кода.
Сравнение производительности
На Рисунке 1 и в Таблице 1 приведены зависимости времени выполнения тестовой программы (в секундах) от размера сетки n, полученные при запуске C-кода (кривая CUDA C) и python-реализаций с библиотекой Numba и двумерными массивами (Numba 2DArr), с библиотекой Numba и одномерными массивами (Numba 1DArr), с библиотекой PyCUDA (кривая PyCUDA).

Рисунок 1
| n | Cuda C | Numba 2DArr | Numba 1DArr | PyCUDA |
|---|---|---|---|---|
| 512 | 0.25 | 0.8 | 0.66 | 0.216 |
| 1024 | 0.77 | 3.26 | 1.03 | 0.808 |
| 2048 | 2.73 | 12.23 | 4.07 | 2.87 |
| 3073 | 6.1 | 27.3 | 9.12 | 6.6 |
| 4096 | 11.05 | 55.88 | 16.27 | 12.02 |
На Рисунке 2 приведены отношения времени выполнения различных python-реализаций к времени выполнения C-кода. Как видно из рисунков, самой медленной, из рассмотренных, является реализация с помощью библиотеки Numba с использованием двумерных массивов. При этом, этот подход является самым наглядным и простым. Интересно, что развертка двумерных массивов в одномерные приводит к примерно троекратному ускорению кода. Самым быстрым решением оказалось использование библиотеки PyCUDA. В то же время, как отмечалось выше, использование этой библиотеки несколько более трудоемко, поскольку требует написания ядра на C. Однако затраты окупаются и скорость выполнения такой python-программы всего на 5-8% меньше чем программы, написанной полностью на C.
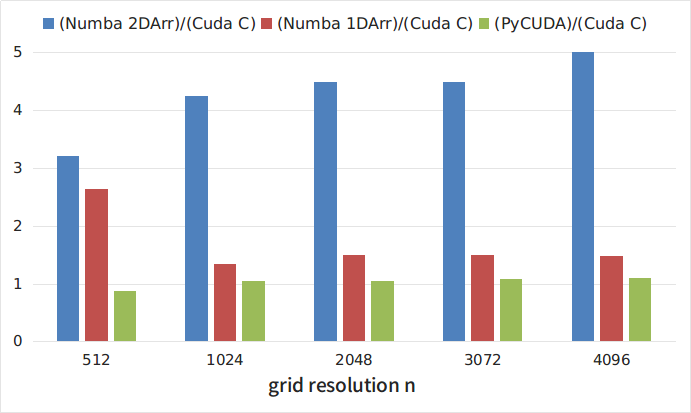
Рисунок 2
Выводы
Чудес не бывает и самые простые и наглядные решения оказываются одновременно и самыми медленными. В то же время, имеющиеся библиотеки позволяют добиться скорости выполнения python-программ, сравнимой со скоростью выполнения чистого C-кода. Существующие библиотеки дают разработчику выбор между более и менее высокоуровневыми решениями. Этот выбор, однако, всегда есть компромисс между скоростью разработки и скоростью выполнения программы.
Ссылки
» Документация библиотеки Numba
» Примеры использования Numba
» Документация библиотеки PyCUDA
» Примеры использования PyCUDA
Комментарии (42)

f_rom
11.12.2016 11:45Я не совсем понял Ваш вопрос. И Numba и PyCUDA — это библиотеки для питона. Синтаксис их использования отличается. В Numbe ядро (функция выполняемая на GPU) вы пишете по сути на питоне. В PyCUDA вы пишете ядро на C и вставляете в свой код на питоне. В итоге самым быстрым оказался C и PyCUDA. Про какое «готовое специализированое ПО» Вы спрашиваете я не очень понял, весь код тут самописный и используются библиотеки для jit компиляции.

renskiy
11.12.2016 13:13Так на каком способе вы в итоге остановились для решения ваших задач? Numba с одномерным массивом вроде выглядит вполне разумным компромиссом.

f_rom
11.12.2016 15:47Мое чисто субъективное мнение состоит в том, что для расчетов занимающих время в пределах 1-10-30 минут на один кейс Numba с одномерными массивами мне подойдет т.к. время на разработку, а также анализ результатов и т.п. нивелирует несколько большее время расчетов. Для расчетов занимающих часы я бы уже использовал PyCUDA или C. Поэтому для ближайшей задачи — PyCUDA.

Meklon
11.12.2016 14:03+10Хотел замечание по самому графику сделать. Неудачная раскладка цветов. Неразличимы напрочь. Воспринимаются как красный и какие-то сине-серо-фиолетовые. Seaborn не смотрели в качестве библиотеки для визуализации?

Lucidus
11.12.2016 15:37При этом, однако, очень важно не терять в скорости выполнения программ, поскольку некоторые расчеты могут занимать от нескольких часов до суток.
Очевидно, в данном случае или С, или РуCUDA. Сравнить только по трудозатратам.
f_rom
11.12.2016 15:56После исследования производительности, представленного в статье именно такой вывод я для себя и сделал. Однако изначально результат для меня был не очевиден. Во-первых, я не был уверен что на питоне мне удастся настолько приблизится к C. Во-вторых, была надежда, что если это возможно, то и Numba позволит получить приемлемое время по отношению к C
По трудозатратам на мой взгляд питон менее трудозаиратен, но вообще все конечно будет зависеть от конкретных задач. Мне полученные результаты дали ориентир.

EvilGenius18
11.12.2016 15:37-11. Библиотеки являются частью Python
2. Из сотен возможных способов реализовать данный расчет, выбираем самую быструю библотеку
3. Получаем идентичные результаты по скорости расчета, в сравнении с С
В чем же тогда:
«известная всем медлительность питона» ?
На Python есть несколько потенциальных способов реализации расчета -> выбираем самый быстрый
На C есть несколько потенциальных способов реализации расчета -> выбираем самый быстрый
Скорость зависит от метода, а не от языка. Как вы сами только что доказали.
0xd34df00d
11.12.2016 20:56+2Медлительность в том, что самым быстрым вариантом оказывается не нативная реализация, а ffi в C.

vasiliysenin
12.12.2016 03:47+1Программа на Си преобразуется в машинный код, а программа на питоне интерпретируется. Поэтому сравнивать надо Numba с РуCUDA. Из тестов видно что Numba медленнее в 3-5 раз.
То есть скорость зависит от языка значительно.
И 3-5 раз это ещё очень хороший результат. Например на The Computer Language Benchmarks Game ( http://benchmarksgame.alioth.debian.org/ ) в тесте mandelbrot ( http://benchmarksgame.alioth.debian.org/u64q/performance.php?test=mandelbrot ) для однопоточной программы C++ g++ #5 отставание от лучшего результата оказалось 7,8 раза, а для Python 3 #7 отставание в 94 раза, при полной загрузке четырёх ядер. То есть разница, по сравнению с однопоточной программой 12 кратная.
Nikobraz
11.12.2016 21:53Чертовски хотел бы увидеть данное сравнение на современных GPU, а то на GTX 580 стоит чип GF110, в котором поддерживается CUDA версии 2.0 в то время как текущая 6.1.

rafuck
11.12.2016 22:08Да тут, судя по коду ядра, вообще без разницы, каким образом получен байт-код для GPU. Более того, код на питоне выглядит абсолютно также, как код на C, ничуть не проще и не короче. По-моему на самом деле здесь вообще измерялась скорость запуска в цикле одного и того же ядра на GPU из разных окружений.

basilbasilbasil
13.12.2016 04:04зато на 580 fp64-блоков больше.
vlanko
13.12.2016 12:35На 580 fp64-блоки официально отключены (производительность в 8 раз ниже fp32)
Nikobraz
15.12.2016 03:47А на GTX 950 FP64 = 1/32 FP32 это как назвать?
FP64=1572 GFLOPS
FP32=49 GFLOPS
Вот табличка, сам инфу по сети собирал

Anton_Menshov
11.12.2016 22:04Немножечко критики:
Расчеты показывают, что для N = 512 время выполнения C-программы распараллеленной на GPU составляет 0.27 секунд против 33.06 секунд для последовательной реализации алгоритма на CPU. То есть ускорение CPU/GPU составляет около 120 раз. С ростом N величина ускорения не убывает.
Немного некорректное сравнение. Следовало бы сравнивать OpenMP (или что-то еще) CPU с GPU. Иначе вы от процессора используете в лучшем случае только четверть, тогда как от GPU — гораздо больше. Иначе создается впечатление, что данная GPU — в 120 раз быстрее процессора, что далеко не так.
+ всегда очень хочется видеть графики в log-log формате. Это стандартный вариант представление времени исполения от величины неизвестных.
Насколько я понимаю в GPGPU, важно чтобы размер данных вмещался в память видеокарты. Таким образом, имеем дисбаланс в 1.5 Gb по видеопамяти и 8 Gb оперативной. Что произойдет, когда памяти в системе еще будет достаточно, а вот видеопамяти уже хавтать не будет? (точно — для N=16384). Произойдет резкий спад производительности GPU — или программа просто вылетит с ошибкой malloc при попытке cudaMemcpy()?
Кроме того, было бы тоже интересно посмотреть, как себя ведет cuda и различные варианты написанной программы на сетках меньших размеров (именно там эффективность параллелизации падает значительно): 256, 128, 64… Ибо чем больше данных — пока они влезают в память единого времени доступа — параллелизация будет только выигрывать.

rafuck
11.12.2016 22:15+1Уточнение: вылетит на cudaMalloc. По поводу OpenMP/Cilk/etc, какой смысл? Насколько я понимаю, процитированный вами абзац — лишь лирическое отступление. На самом деле автор хотел понять, имеет ли смысл использовать те или иные биндинги к CUDA из Python.

Anton_Menshov
12.12.2016 01:32Спасибо за уточнение :)
Пожалуй, вы правы — и это есть лирическое отступление в чистом виде. Я лишь зацепился, ибо в том числе регулярно занимаюсь бенчмаркингом в численных задачах, как на CPU, GPU, мат. сопроцессорах, включая гетерогенные и многоузловые конфигурации. Часто встречаю заявления, что GPU лучше чем CPU — и насколько (без указания стоимости, ваттов или чего бы то еще). Если читать эту статью по диагонали, кроме обзора биндингов CUDA к Python, можно сделать вывод, что был достигнут прирост в 120 раз (при этом справедливо написано, что по отношению к непараллельному CPU) и GPU — лучше в сотню раз.

f_rom
12.12.2016 05:08Должен согласится с Вашими утверждениями, однако, меня интересовало сравнение времени выполнения для задач и сеток характерных для практических задач, которые мне уже доводилось или предстоит решать. В этих задачах я не использую ни очень большие (N>=16384) ни очень маленькие (N<256) сетки. Что касается параллельной реализации на CPU, я проводил тесты с использованием MPI и получал прирост скорости (CPU 4 ядра)/GPU порядка 35-40 раз на интересующих меня сетках. По поводу энергопотребления, это конечно тоже важно, но за свет платим не мы (хотя я понимаю значение этого фактора для экологии). Вообще детальное сравнение CPU vs. GPU тема для отдельной статьи и таких статей можно найти достаточно много, в этой статье я лишь упомянул один результат не претендуя на сколько-нибудь детальное сравнение

rafuck
11.12.2016 22:26+1Надо сказать, результат для такого примера вполне ожидаемый. У меня один вопрос, почему в PyCUDA параметры
int* dN, double* dth2передаются через аргументы в виде указателей в общую память, а не пишутся в константную память как в примере на C? Этого нельзя было сделать?

f_rom
12.12.2016 05:12К сожалению я не нашел способа как в PyCUDA передать переменные через константную память и поэтому использовал такой способ. Буду очень благодарен если кто-нибудь покажет как это сделать.

rafuck
12.12.2016 10:15+1Я не знаток PyCUDA, но ответ на этот вопрос гуглится на раз.
1) В коде ядра
__device__ __constant__ int dN; __device__ __constant__ double dth2;
2) В питоне
from pycuda.compiler import SourceModule module = SourceModule(kernelCode) dN = module.get_global('dN')[0] cuda.memcpy_htod(dN, valueOnHost)
В любом случае такой подход с внедрением сишного исходника в Python-скрипт выглядит как-то жутковато :)
f_rom
12.12.2016 11:15Должен добавить, что т.к. константная память более быстрая, то после изменения кода в соответствии с Вашим комментарием отношение PyCuda/CudaC стало не более 2-2.5%

rafuck
12.12.2016 11:24Я вообще ожидал разницу в пределах погрешности измерений :) Я уже писал об этом где-то выше. Вы запускаете идентичный код ядра из разных окружений.

rafuck
12.12.2016 11:35И еще. По коду я не хотел критиковать. Но все же скажу, что учет условий Дирихле следовало сделать без if-else. Скорее всего, это несколько ускорило бы программу.
Я это к чему. Если не трудно, попробуйте, пожалуйста в сишном коде поменять выражения if-else на тернарный оператор. Чисто теоретически можете получить выигрыш (зависит от того, насколько умным стал nvcc)

Maxpt1
12.12.2016 03:46Я сразу извиняюсь, что не совсем по теме, но может от явной разностной схемы перейти к неявной? Конечно, при одинаковом N для ЯРС приходится делать в два раза меньше вычислений, чем для НРС, но зато можно ограничиться меньшим N.

f_rom
12.12.2016 05:21Преимущество неявной схемы заключается не в меньшем значении N, потому что N пространственное разрешение сетки и соответственно задает точность (грубо говоря) решения, а в возможности снять ограничение на шаг по времени. Поэтому, что бы просчитать одинаковые времена НРС требует сделать меньше временных шагов, однако при этом число операций на шаг больше. Выбор ЯРС для тестовой задачи был связан с тем, какую реальную задачу мы собирались решать, т.к. мы хотели смоделировать те условия которые будут там. Так вот, в этих задачах есть сильно нелинейные члены и как показали предыдущие сравнения сильно увеличить шаг по времени с использованием НРС не удается и большее количество операций, требующихся на обращения матриц, не окупается.
Вы правы в том, что для других задач НРС — хороший выход и конечно мы будем сравнивать производительность операций с разреженными матрицами в дальнейшем и по мере необходимости

pirate_tony
12.12.2016 08:02-1Я заранее напишу что спорить не хочу.
И вообщем-то всё неплохо но не знаю почему ни одного слова про OpenCL не было, даже в сравнении. Это ведь открытый стандарт и как показывает практика более эффективный для математических вычислений.
RomanArzumanyan
12.12.2016 09:39OpenCL гарантирует conformance (переносимость кода), но не performance (производительность). По-настоящему быстрые решения всегда привязаны к аппаратному вендору.


Onito
Я правильно понял что в итоге самые быстрые результаты показал C и либа которая стартует из питона написанная на C/C++? В итоге вывод такой — в частных случаях использование готового специализированного ПО занимает меньше времени а показывает те же результаты.
f_rom
Я не совсем понял Ваш вопрос. И Numba и PyCUDA — это библиотеки для питона. Синтаксис их использования отличается. В Numbe ядро (функция выполняемая на GPU) вы пишете по сути на питоне. В PyCUDA вы пишете ядро на C и вставляете в свой код на питоне. В итоге самым быстрым оказался C и PyCUDA. Про какое «готовое специализированое ПО» Вы спрашиваете я не очень понял, весь код тут самописный и используются библиотеки для jit компиляции.
Onito
Как я понял PyCUDA облегчает жизнь и позволяет писать меньше кода, хотя по сути пишешь(и в результате всё работает) на том же C, её я и назвал спец решением, а реализацию на чистом C велосипедом. Вывод что я написал как бы обобщающий — что вообще в любых задачах не редко лучше использовать готовое решение(или решение заточенное под конкретную задачу) а не писать велосипеды и вывод данной статьи говорит о том же.