19.01.2017 18:32
dfedchenko 21 6000 Источник
Одним из красивейших математических результатов можно смело считать теорему Эйлера, которая впервые появилась в журнале Петербургской Академии наук в работах Леонарда Эйлера «Элементы учения о телах» и «Доказательство некоторых замечательных свойств, которым подчинены тела, ограниченные плоскими гранями».

Теорема Эйлера. Пусть ${\rm B}$ – число вершин выпуклого многогранника, ${\rm P}$ – число его ребер и $\Gamma$ – число граней. Тогда верно равенство

$ {\rm B} - {\rm P} + \Gamma = 2. $


Число $\chi = {\rm B} - {\rm P} + \Gamma$ называется эйлеровой характеристикой многогранника. Легко вычислить эйлерову характеристику для некоторых знакомых нам многогранников.

Многогранник ${\rm B}$ ${\rm P}$ $\Gamma$ $\chi$
Тетраэдр 4 6 4 2
Куб 8 12 6 2
Октаэдр 6 12 8 2

Доказательство теоремы Эйлера может быть найдено здесь.

Давайте воспользуемся теоремой Эйлера для установления некоторых интересных фактов. Посмотрите на изображение футбольного мяча.


Вопрос: сколько нужно взять пятиугольников, чтобы сшить мяч? Пусть $x$ – количество шестиугольников, а $y$ – количество пятиугольников. Давайте применим теорему Эйлера к нашему футбольному мячу:

$ {\rm B} - {\rm P} + \Gamma = 2, $


где ${\rm B} = \frac{6x + 5y}{3}$, ${\rm P} = \frac{6x+5y}{2}$, а $\Gamma = x+y$. Формулы для количества вершин, ребер и граней легко получаются из наблюдения, что каждая вершина попадает на три грани, а по каждому ребру пересекаются только две грани. Подставив значения в формулу, вы получите ответ: $y=12$. Переменная $x$ исключается из уравнения, т.е. количество шестиугольников может быть каким угодно. На следующей картинке изображен мяч, сшитый из одних только пятиугольников. Сколько их?



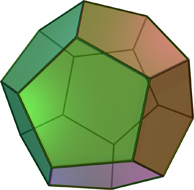
Этот многогранник называется додекаэдром и является одним из пяти правильных многогранников.



Давайте рассмотрим другой сюжет. Фуллерены — молекулярные соединения, принадлежащие классу аллотропных форм углерода и представляющие собой выпуклые замкнутые многогранники, составленные из чётного числа трёхкоординированных атомов углерода. Своим названием фуллерены обязаны инженеру и архитектору Ричарду Бакминстеру Фуллеру, чьи геодезические конструкции построены по этому принципу. Первоначально данный класс соединений был ограничен лишь структурами, включающими только пятиугольные и шестиугольные грани.



И наконец, давайте посмотрим на следующую картинку.




Ничего особенного — всего лишь купол, собранный из шестиугольников. А теперь еще раз помедитируйте над формулой Эйлера и вперед искать пятиугольники.




Этот и многие другие математические сюжеты смотрите в замечательных лекциях Алексея Савватеева или в его книге «Математика для гуманитариев».

Поделиться с друзьями
-->

Комментарии (21)


  1. Zenitchik
    19.01.2017 21:38
    #10023406

    Это для тех, кому лень заглянуть в Википедию?


    1. dfedchenko
      19.01.2017 21:58
      #10023424
      +2

      Ну конечно.


    1. Idot
      20.01.2017 07:38
      #10023766

      Это для тех кто не верит написанному в Википедии, и не считает ссылку на Википедию пруфом.


      1. Zenitchik
        20.01.2017 12:48
        #10024300

        А с чего бы этим людям верить пересказу того же самого на Гиктаймсе? Тем более — более сжатому?


  1. Fen1kz
    19.01.2017 23:08
    #10023506
    +1

    Спасибо за прекрасную иллюстрацию к большиству математических статей:


    Давайте применим теорему Эйлера к нашему футбольному мячу: В — Р + Г = 2
    где В = (6х+5у) / 2

    aka: Ля-ля, тут математика это весело, давайте рассчитаем что-то для мячика. И сразу "Бдыщь", тут домножаем, тут делим на 3, это же так легко


    легко получаются из наблюдения, что каждая вершина попадает на три грани, а по каждому ребру пересекаются только две грани.

    То есть вот сразу так, действительно, легкая логика. Только таких логик ещё миллион. Может быть В = 3 * (5/х + 6/у), а? Тут тоже такая же легкая адекватная логика. То бишь вообще не объяснено почему "количество шестиугольников надо умножить на шесть, а количество пятиугольников на пять и поделить на то сколько каждая вершина попадает на грани" это правильно, а "количество сторон разделить на количество многоугольников, сложить и разделить на точки соприкосновения." это неправильно.


    tl;dr Такая математика совсем не познавательная =(


    1. ainoneko
      20.01.2017 06:44
      #10023740
      +3

      не объяснено почему «количество шестиугольников надо умножить на шесть, а количество пятиугольников на пять и поделить на то сколько каждая вершина попадает на грани» это правильно

      Потому что в N-угольнике ровно N углов? (Кэп спешит на помощь.)
      Потому что в общее количество всех углов всех многоугольников каждая вершина многогранника входит 3 раза? (Кэп никуда не уходил.)


      1. dfedchenko
        20.01.2017 09:05
        #10023836
        +1

        Спасибо Кэп. Никак не мог подобрать правильных слов.


    1. VioletGiraffe
      20.01.2017 20:18
      #10025622

      Профессор читает лекцию по математике. Выписывает на доске длиннющую, совершенно необозримую формулу и заявив: «Отсюда с очевидностью следует...» выписывает еще более громоздкую формулу. На минуту задумывается, потом, извинившись, выходит из аудитории. Примерно через полчаса возвращается и, небрежно бросив на кафедру кипу исписанной бумаги, заявляет:
      — Да, это действительно очевидно, — и продолжает лекцию.


  1. atumisnamor
    19.01.2017 23:45
    #10023554

    А кто спроектировал эти конструкции и почему фуллерены так называют?


    1. dfedchenko
      20.01.2017 05:42
      #10023714

      Фуллерены названы по имени архитектора Фуллера. Меня больше интересовала цифра 12.


      1. saluev
        20.01.2017 13:34
        #10024454

        12 — число.


        1. mammuthus
          20.01.2017 19:52
          #10025568

          Зависит от алфавита.


  1. AndreyDmitriev
    20.01.2017 08:34
    #10023806
    +1

    … т.е. количество шестиугольников может быть каким угодно...

    Любопытный читатель из Аренсбурга интересуется — а как будет выглядеть футбольный мяч, сшитый из двенадцати пятиугольников и одного шестиугольника?


    1. dfedchenko
      20.01.2017 09:01
      #10023828
      +1

      Я ведь как в том анекдоте — всего лишь стратег, а не тактик. Но теория однозначно утверждает, что взяв 12 правильных 5-угольников и 1 правильный 6-угольник с равной длиной ребра, вы склеите гомеоморф сферы (как завернул), т.е. мяч. При наличии цветного картона, ножниц, линейки, а также циркуля, умения извлекать корни из комплексных чисел и пары часов свободного времени свет увидит интересующую вас конструкцию. Другой вопрос: захотите ли вы им играть в футбол.


      1. gurux13
        20.01.2017 09:19
        #10023860
        +2

        Выполнение условий теоремы Эйлера ведь не является достаточным условием существования многогранника? Существование чисел В, Г, Р из условия не гарантирует существования многогранника с таким числом вершин, граней, ребёр (В = 3, Г = 2, Р = 2).
        То есть, теория утверждает, что с числом пятиугольников, не равным 12, Вы гомеоморф сферы из пятиугольников и шестиугольников не сделаете. Обратное, вообще говоря, не утверждается — нужно пробовать. Или есть какая-то ещё теория, которой Вы пользуетесь?
        P.S. зачем Вам корни из комплексных чисел?


        1. dfedchenko
          20.01.2017 11:16
          #10024054

          Я утверждаю, что с числом 5-угольников не равным 12 не сошьешь футбольный мяч из 5 и 6-угольников. Футбольный мяч — выпуклый многогранник с В, Р и Г, указанными в статье (т.е. мы фиксируем сшивку: в каждой вершине сходятся три ребра и каждые две грани имеют одно смежное ребро). Пирамида Хеопса, например, нам не подходит, т.к. в вершине сходятся четыре ребра. Другие вещи следует аккуратно считать отдельно. Правильные N-угольники удобно реализовывать как корни N-ой степени из комплексного числа z.


          1. gurux13
            20.01.2017 11:47
            #10024132

            теория однозначно утверждает, что взяв 12 правильных 5-угольников и 1 правильный 6-угольник с равной длиной ребра, вы склеите гомеоморф сферы

            Вы заставляете меня цитировать :)


            А правильный пятиугольник и шестиугольник, насколько я помню школьную программу, рисуются без знания об i :) Вот только как сделать их с совпадающей длиной стороны я не знаю.


    1. Gurklum
      20.01.2017 11:03
      #10024034
      +1

      Возьмите додекаэдр. Возьмите любую его вершину. Из неё выходит 3 ребра. Разрежьте все это мероприятие вдоль этих трех ребер и «распахните». Пятиугольников останется 12. Пустота будет соответствовать шестиугольнику.
      Не сказать, что выпуклому, а тем более правильному, однако шестиугольнику.


      1. dfedchenko
        20.01.2017 11:05
        #10024042

        Вы похоже правы. Нет под рукой додекаэдра. Думаю, в этот разрез очень удачно (выпукло) впишется 6-угольник.


        1. AndreyDmitriev
          20.01.2017 11:46
          #10024130

          Выпукло не получится. Как вы понимаете, разрезав додекаэдр вдоль трёх ребер, вы получите отверстие в форме шестиугольника, которое будет образовано тремя пятиугольниками, то есть каждые два ребра нашего шестиугольника будут совпадать с двумя рёбрами каждого из трёх пятиугольников. Вот как бы вы не старались, но приложить выпуклый шестиугольник к выпуклому пятиугольнику так, чтобы два ребра совпали, ну никак не получится.


        1. AndreyDmitriev
          20.01.2017 12:30
          #10024242

          Да, вдогонку — я не утверждаю, что это невозможно, просто там чуть хитрее всё — грубо говоря, надо к шестиугольнику вначале приклеить шесть пятиугольников, а затем оставшиеся шесть.
          Единственно, в чём у меня возникают сильные сомнения, так это в том, что многогранники останутся правильными. Теорема Эйлера применима к выпуклым многогранникам, но не утвержает, что они должны быть правильными.