Оффтоп
В названии статьи не поместилось — данные результаты считаются таковыми по версии рейтинга Graph500. Также хотелось бы выразить благодарность компаниям IBM и RSC за предоставленные ресурсы для проведения экспериментальных запусков во время исследования.
Введение
Поиск в ширину (BFS) является одним из основных алгоритмов обхода графа и базовым для многих алгоритмов анализа графов более высокого уровня. Поиск в ширину на графах является задачей с нерегулярным доступом к памяти и с нерегулярной зависимостью по данным, что сильно усложняет его распараллеливание на все существующие архитектуры. В статье будет рассмотрена реализация алгоритма поиска в ширину (основного теста рейтинга Graph500) для обработки больших графов на различных архитектурах: Intel х86, IBM Power8+, Intel KNL и NVidia GPU. Будут описаны особенности реализации алгоритма на общей памяти, а также преобразования графа, которые позволяют достичь рекордных показателей производительности и энергоэффективности на данном алгоритме среди всех одноузловых систем рейтинга Graph500 и GreenGraph500.
В последнее время все большую роль играют графические ускорители (ГПУ) в неграфических вычислениях. Потребность их использования обусловлена их относительно высокой производительностью и более низкой стоимостью. Как известно, на ГПУ и центральных процессорах (ЦПУ) хорошо решаются задачи на структурных, регулярных сетках, где параллелизм так или иначе легко выделяется. Но есть задачи, которые требуют больших мощностей и используют неструктурированные сетки или данные. Примером таких задач являются: Single Shortest Source Path problem (SSSP) — задача поиска кратчайших путей от заданной вершины до всех остальных во взвешенном графе, задача Breadth First Search (BFS [1]) — задача поиска в ширину в неориентированном графе, Minimum Spanning Tree (MST, например, зарубежная и моя реализации) — задача поиска сильно связанных компонент и другие.
Данные задачи являются базовыми в ряде алгоритмов на графах. На данный момент алгоритмы BFS и SSSP используются для ранжирования вычислительных машин в рейтингах Graph500 и GreenGraph500. Алгоритм BFS (breadth-first search или поиск в ширину) является одним из наиболее важных алгоритмов анализа на графах. Он используется для получения некоторых свойств связей между узлами в заданном графе. В основном BFS используется как звено, например, в таких алгоритмах, как нахождение связных компонент [2], нахождение максимального потока [3], нахождение центральных компонент (betweenness сentrality) [4, 5], кластеризация [6], и многие другие.
Алгоритм BFS имеет линейную вычислительную сложность O(n + m), где n — количество вершин и m — количество ребер графа. Данная вычислительная сложность является наиболее оптимальной для последовательной реализации. Но данная оценка вычислительной сложности не применима для параллельной реализации, так как последовательная реализация (например, с помощью алгоритма Дейкстры) имеет зависимости по данным, что препятствует ее распараллеливание. Также производительность данного алгоритма ограничена производительностью памяти той или иной архитектуры. Поэтому наибольшее значение имеют оптимизации, направленные на улучшение работы с памятью всех уровней.
Обзор существующих решений и рейтинг Graph500
Graph500 и GreenGraph500
Рейтинг Graph500 был создан как альтернатива рейтингу Top500. Данный рейтинг используется для ранжирования вычислительных машин в приложениях, которые используют нерегулярный доступ к памяти, в отличие от последнего. Для тестируемого приложения в рейтинге Graph500 пропускная способность памяти и коммуникационной сети играют наиболее важную роль. Рейтинг GreenGraph500 является альтернативой рейтинга Green500 и используется в дополнении к Graph500.
В Graph500 используется метрика — количество обработанных ребер графа в секунду (TEPS — traversed edges per second), в то время как в GreenGraph500 используется метрика — количество обработанных ребер графа в секунду на один ватт. Таким образом, первый рейтинг ранжирует вычислительные машины по скорости вычисления, а второй — по энергоэффективности. Данные рейтинги обновляются каждые полгода.
Существующие решения
Алгоритм поиска в ширину был придуман более 50 лет назад. И до сих пор проводятся исследования для эффективной параллельной реализации на различных устройствах. Данный алгоритм показывает на сколько хорошо организована работа с памятью и коммуникационной средой вычислителей. Существует достаточно много работ по распараллеливанию данного алгоритма на x86 системах [7-11] и на ГПУ [12-13]. Также подробные результаты выполнения реализованных алгоритмов можно увидеть в рейтингах Green500 и GreenGraph500. К сожалению, алгоритмы многих эффективных реализаций не опубликованы в зарубежных источниках.
Если выбрать только одноузловые системы в рейтинге Graph500, то мы получим следующие некоторые данные, которые представлены в таблице ниже. Результаты, описанные в данной работе, помечены жирным шрифтом. В таблицу включались графы с количеством вершин более 225. Из полученных данных видно, что на текущий момент не существует более эффективной реализации с использованием только одного узла, чем предложенная в данной статье. Более подробный анализ представлен в разделе Анализа полученных результатов.
| Позиция | Система | Размер 2N | GTEPS | Ватт |
|---|---|---|---|---|
| 50 | GPU NVidia Tesla P100 | 26 | 204 | 175 |
| 67 | GPU NVidia GTX Titan | 25 | 114 | 212 |
| 76 | 4x Intel Xeon E7-4890 v2 | 32 | 55.9 | 1153 |
| 86 | GPU NVidia Tesla P100 | 30 | 41.7 | 235 |
| 103 | GPU NVidia GTX Titan | 25 | 17.2 | 233.8 |
| 104 | Intel Xeon E5 2699 v3 | 30 | 16.3 | 145 |
| 106 | 4x AMD Radeon R9 Nano GPUs | 25 | 15.8 | |
| 112 | IBM POWER8+ | 30 | 13.2 | 200 |
Формат хранения графа
Для оценки производительности алгоритма BFS используются неориентированные RMAT графы. RMAT графы хорошо моделируют реальные графы из социальных сетей, Интернета. В данном случае рассматриваются RMAT графы со средней степенью связности вершины 16, а количество вершин является степенью двойки. В таком RMAT графе имеется одна большая связная компонента и некоторое количество небольших связных компонент или висящих вершин. Сильная связность компонент не позволяет каким-либо образом разделить граф на такие подграфы, которые помещались бы в кэш память.
Для построения графа используется генератор, который предоставляется разработчиками рейтинга Graph500. Данный генератор создает неориентированный граф в формате RMAT, причем выходные данные представлены в виде набора ребер графа. Такой формат не очень удобен для эффективной параллельной реализации графовых алгоритмов, так как необходимо иметь агрегированную информацию по каждой вершине, а именно — какие вершины являются соседями для данной. Удобный для этого представления формат называется CSR (Compressed Sparse Rows).
Данный формат получил широкое распространение для хранения разреженных матриц и графов. Для неориентированного графа с N вершинами и M ребрами необходимо два массива: X (массив указателей на смежные вершины) и А (массив списка смежных вершин). Массив X размера N + 1, а массив А — 2 * M, так как в неориентированном графе для любой пары вершин необходимо хранить прямую и обратную дуги. В массиве X хранятся начало и конец списка соседей, находящиеся в массиве А, то есть весь список соседей вершины J находится в массиве A с индекса X[J] до X[J+1], не включая его. Для иллюстрации на рисунке ниже слева показан граф из 4 вершин, записанный с помощью матрицы смежности, а справа – в формате CSR.
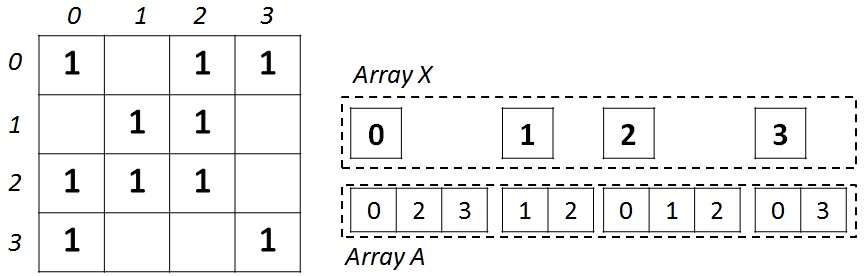
После преобразования графа в CSR-формат, необходимо проделать еще некоторую работу над входным графом для улучшения эффективности работы кэша и памяти вычислительных устройств. После выполнения описанных ниже преобразований, граф остается все в том же CSR-формате, но приобретет некоторые свойства, связанные с выполненными преобразованиями.
Введенные преобразования позволяют построить граф в оптимальном виде для большинства алгоритмов обхода графа в формате CSR. Добавление новой вершины в граф не приведет к выполнению всех преобразований заново, достаточно следовать введенным правилам и добавлять вершину так, чтобы общий порядок вершин не нарушался.
Локальная сортировка списка вершин
Для каждой вершины выполним сортировку по возрастанию ее списка соседей. В качестве ключа для сортировки будем использовать количество соседей для каждой сортируемой вершины. После выполнения данной сортировки, выполняя обход списка соседей у каждой вершины, мы будем обрабатывать сначала самые тяжелые вершины — вершины, имеющие большое количество соседей. Данную сортировку можно выполнять независимо для каждой вершины и параллельно. После выполнения данной сортировки, номера вершин графа в памяти не изменяется.
Глобальная сортировка списка вершин
Для списка всех вершин графа выполним сортировку по возрастанию. В качестве ключа будем использовать количество соседей для каждой из вершин. В отличие от локальной сортировки, данная сортировка требует перенумерации полученных вершин, так как меняется позиция вершины в списке. Процедура сортировки имеет сложность O(N*log(N)) и выполняется последовательно, а процедура перенумерации вершин может быть выполнена параллельно и по скорости работы сопоставима с временем копирования одного участка памяти в другой.
Перенумерация всех вершин графа
Занумеруем вершины графа таким образом, чтобы наиболее связные вершины имели наиболее близкие номера. Данная процедура устроена следующим образом. Сначала берется первая вершина из списка для перенумерации. Она получает номер 0. Затем все соседние вершины с рассматриваемой вершиной добавляются в очередь для перенумерации. Следующая вершина из списка перенумерации получает номер 1 и так далее. В результате данной операции в каждой связной компоненте разница между максимальным и минимальным номером вершины будет наименьшей, что позволит лучшим образом использовать маленький объем кэша вычислительных устройств.
Реализация алгоритма
Алгоритм поиска в ширину в неориентированном графе устроен следующим образом. На входе подается начальная за ранее неопределенная вершина в графе (корневая вершина для поиска). Алгоритм должен определить, на каком уровне, начиная от корневой вершины, находится каждая из вершин в графе. Под уровнем понимается минимальное количество ребер, которое необходимо преодолеть, чтобы добраться из корневой вершины в отличную от корневой вершину. Также для каждой из вершин, кроме корневой, необходимо определить вершину родителя. Так как у одной вершины может быть несколько родительских вершин, то в качестве ответа принимается любая из них.
Алгоритм поиска в ширину имеет несколько реализаций. Наиболее эффективная реализация — итерационный обход графа с синхронизацией по уровню. Каждый шаг представляет собой итерацию алгоритма, на которой информация с уровня J переносится на уровень J+1. Псевдокод последовательного алгоритма представлен по ссылке.
Параллельная реализация базируется на гибридном алгоритме, состоящий из top-down (TD) и bottom-up (BU) процедур, который был предложен автором данной статьи [11]. Суть данного алгоритма заключается в следующем. Процедура TD позволяет обойти вершины графа в прямом порядке, то есть, перебирая вершины, мы рассматриваем связи как родитель-потомок. Вторая процедура BU позволяет обойти вершины в обратном порядке, то есть, перебирая вершины, мы рассматриваем связи как потомок-родитель.
Рассмотрим последовательную реализацию гибридного алгоритма TD-BU, псевдокод которой показан ниже. Для обработки графа вершин нам необходимо создать дополнительные два массива-очереди, которые будут содержать в себе набор вершин на текущем уровне — Qcurr, и набор вершин на следующем уровне — Qnext. Чтобы выполнять более быстрые проверки существования вершины в очереди, необходимо ввести массив посещенных вершин. Но так как нам в результате работы алгоритма необходимо получить информацию о том, на каком уровне располагается каждая из вершин, этот массив может быть использован и в качестве индикатора посещенных и размеченных вершин.
Последовательный гибридный алгоритм BFS:
void bfs_hybrid(G, N, M, Vstart) {
Levels <- (-1); Parents <- (N + 1); Qcurr+=Vstart; CountQ=lvl=1;
while (CountQ) {
CountQ = 0; vis = 0; inLvl = 0;
if (state == TD)
foreach Vi in Qcurr
foreach Vk in G.Edges(Vi)
inLvl++;
if (Levels[Vk] == -1)
Qnext += Vk; Levels[Vk] = lvl; Parents[Vk] = Vi; vis++;
else if (state == BU)
foreach Vi in G
if (Levels[Vi] == -1)
foreach Vk in G.Edges(Vi)
inLvl++;
if (Levels[Vk] == lvl - 1)
Qnext += Vi; Levels[Vi] = lvl; Parents[Vi] = Vk; vis++;
break;
change_state(Qcurr, Qnext, vis, inLvl, G);
Qcurr <- Qnext; CountQ = Qnext.size();
}
}Основной цикл работы алгоритма состоит из последовательной обработки каждой вершины, находящейся в очереди Qcurr. Если в очереди Qcurr больше не остается вершин, то алгоритм останавливается и ответ получен.
В самом начале алгоритма начинает работать процедура TD, так как в очереди содержится всего одна вершина. В процедуре TD мы для каждой вершины Vi из очереди Qcurr просматриваем список соседних с этой вершиной Vk и добавляем в очередь Qnext тех из них, которые еще не были помечены как посещенные. Также все такие вершины Vk получают номер текущего уровня и родительскую вершину Vi. После завершения просмотра всех вершин из очереди Qcurr запускается процедура выбора следующего состояния, которая может либо остаться на процедуре TD для следующей итерации, либо сменить процедуру на BU.
В процедуре BU мы просматриваем вершины не из очереди Qcurr, а те вершины, которые еще не были помечены. Данная информация содержится в массиве уровней Levels. Если такие вершины Vi еще не были размечены, то мы проходим по всем ее соседям Vk и если эти вершины, которые являются родителями для Vi, находятся на предыдущем уровне, то вершина Vi попадает в очередь Qnext. В отличие от процедуры TD, в данной процедуре можно прервать просмотр соседних вершин Vk, так как нам достаточно найти любую родительскую вершину.
Если выполнять поиск только процедурой TD, то на последних итерациях алгоритма список вершин, который необходимо обработать, будет очень большим, а неразмеченных вершин будет достаточно мало. Тем самым процедура будет выполнять лишние действия и лишние обращения в память. Если выполнять поиск только процедурой BU, то на первых итерациях алгоритма будет достаточно много неразмеченных вершин и аналогично процедуре TD, будут выполнены лишние действия и лишние обращения в память.
Получается, что первая процедура эффективна на первых итерациях алгоритма BFS, а вторая — на последних. Ясно, что наибольший эффект будет достигнут, когда мы будем использовать обе процедуры. Для того, чтобы автоматически определять, когда необходимо выполнять переключение с одной процедуры на другую, воспользуемся алгоритмом (процедура change_state), который был предложен авторами данной статьи [11]. Данный алгоритм по информации о количестве обработанных вершин на двух соседних итерациях пытается понять характер поведения обхода. В алгоритме вводится два коэффициента, которые позволяют настраивать переключение с одной процедуры на другую в зависимости от обрабатываемого графа.
Процедура смены состояния может переводить не только TD в BU, но и обратно BU в TD. Последняя смена состояния полезна в том случае, когда количество вершин, которые необходимо просмотреть, достаточно мало. Для этого вводится понятие нарастающего фронта и затухающего фронта размеченных и неразмеченных вершин. Следующий псевдокод, представленный ниже, выполняет смену состояния в зависимости от полученных характеристик на конкретной итерации обхода графа в зависимости от настроенных коэффициентов alpha и beta. Данная функция может быть настроена на любой входной граф в зависимости от factor (под factor понимается средняя связность вершины графа).
Функция изменения состояния:
state change_state(Qcurr, Qnext, vis, inLvl, G)
{
new_state = old_state;
factor = G.M / G.N / 2;
if(Qcurr.size() < Qnext.size()) // Growing phase
if(old_state == TOP_DOWN)
if(inLvl < ((G.N - vis) * factor + G.N) / alpha)
new_state = TOP_DOWN;
else
new_state = BOTTOM_UP;
else // Shrinking phase
if (Qnext.size() < ((G.N - vis) * factor + G.N) / (factor * beta))
new_state = TOP_DOWN;
else
new_state = BOTTOM_UP;
return new_state;
}Описанные выше концепции гибридной реализации алгоритма BFS применялись для параллельной реализации как для ЦПУ подобных систем, так и для ГПУ. Но есть некоторые отличия, которые будут рассмотрены далее.
Параллельная реализация на ЦПУ на общей памяти
Параллельная реализация для ЦПУ систем (Power 8+, Intel KNL и Intel х86) была выполнена с использованием OpenMP. Для запуска использовался один и тот же код, но для каждой платформы выполнялись свои настройки для директив OpenMP, например, задавались разные режимы балансировки нагрузки между нитями (schedule). Для реализации на ЦПУ с использованием OpenMP можно выполнить еще одно преобразование графа, а именно — сжатие списка вершин соседей.
Сжатие заключается в удалении незначащих нулевых битов каждого элемента из массива А, причем данное преобразование делается отдельно для каждого диапазона [Xi, Xi+1). Происходит уплотнение элементов массива А. Такое сжатие позволяет сократить количество используемой памяти для хранения графа примерно на 30% для больших графов порядка 230 вершин и 234 ребер. Для более маленьких графов экономия от такого преобразования пропорционально увеличивается в силу того, что уменьшается количество бит, которое занимает максимальный номер вершины в графе.
Такое преобразование графа накладывает некоторые ограничения на обработку вершин. Во-первых, все соседние вершины должны обрабатываться последовательно, так как они представляют собой сжатую, закодированную определенным образом последовательность элементов. Во-вторых, необходимо выполнять дополнительные действия по распаковке сжатых элементов. Данная процедура не является тривиальной и для ЦПУ Power8+ не позволила получить эффекта. Причиной может быть плохая оптимизация компилятора или отличная от Intel работа аппаратуры.
Для того, чтобы выполнять параллельно одну итерацию алгоритма, необходимо создать свои очереди Qth_next для каждого потока OpenMP. А после выполнения всех циклов, выполнить объединение полученных очередей. Также необходимо локализовать все переменные, по которым есть редукционная зависимость. В качестве оптимизации процедура TD выполняется в последовательном режиме, если в очереди Qcurr количество вершин меньше заданного порога (например, меньше 300). Для графа разного размера, а также в зависимости от архитектуры, данный порог может иметь разные значения. Параллельные директивы располагались перед циклами (foreach Vi in Qcurr) в случае процедуры TD, и (foreach Vi in G) в случае процедуры BU.
Параллельная реализация на ГПУ
Параллельная реализация для ГПУ была выполнена с использованием технологии CUDA. Реализация процедуры TD и BU существенно отличаются в случае использования ГПУ, так как существенно отличается алгоритм доступа к данным во время выполнения той или иной процедуры.
Процедура TD была реализована с помощью динамического параллелизма CUDA. Данная возможность позволяет переложить некоторую работу, связанную с балансировкой нагрузки, на аппаратуру ГПУ. Каждая вершина Vi из очереди Qcurr может содержать абсолютно разное за ранее не известное количество соседей. Из-за этого при прямом отображении всего цикла на набор нитей, возникает сильный дисбаланс нагрузки, так как CUDA позволяет использовать блок нитей фиксированного размера.
Описанная проблема решается путем использования динамического параллелизма. В начале запускаются мастер-нити. Данных нитей будет столько, сколько вершин содержится в очереди Qcurr. Затем каждая мастер-нить запускать столько дополнительных нитей, сколько соседей имеется у вершины Vi. Таким образом, количество используемых нитей формируется в динамике во время выполнения программы в зависимости от входных данных.
Данная процедура не удобна для выполнения на графическом процессоре из-за необходимости использовать динамический параллелизм. При большом суммарном количестве нитей, которые необходимо создать из мастер-нитей, возникают большие накладные расходы. Поэтому переключение на процедуру BU выполняется раньше, чем на ЦПУ.
Процедура BU является более благоприятной для выполнения на ГПУ, если проделать некоторые дополнительные преобразования данных. Данная процедура существенно отличается от процедуры TD тем, что проход выполняется над всеми подряд идущими вершинами графа. Таким образом организованный цикл позволяет выполнить некоторую подготовку данных для хорошего доступа к памяти.
Преобразование заключается в следующем. Известно, что соседние нити одного варпа выполняют инструкции синхронно и параллельно. Также для эффективного доступа к памяти требуется, чтобы соседние нити в варпе обращались к соседним ячейкам в памяти. Для примера положим количество нитей в варпе равным 2. Если каждой нити сопоставить одну вершину цикла (foreach Vi in G), то во время обработки соседей в цикле (foreach Vk in G.Edges(Vi)) каждая нить будет обращаться в свою область памяти, что негативно скажется на производительности, так как соседние нити будут обрабатывать далеко расположенные ячейки в памяти. Для того, чтобы исправить положение, перемешаем элементы массива А таким образом, чтобы доступ к первым двум соседям из V0 и V1 осуществлялся наилучшим образом — соседние элементы располагались в соседних ячейках в памяти. Далее, в памяти таким же образом будут лежать вторые, третьи и т.д. элементы.
Данное правило выравнивания применяется для группы нитей варпа (32 нити): выполняется перемешивание соседей — сначала располагаются первые 32 элемента, затем вторые 32 элемента и т.д. Так как граф отсортирован по убыванию количества соседей, то группы вершин, которые располагаются рядом, будут иметь достаточно близкое количество вершин соседей.
Перемешивать таким способом элементы можно не во всем графе, так как во время работы процедуры BU во внутреннем цикле есть досрочный выход. Описанные выше глобальная и локальная сортировки вершин позволяют выходить из данного цикла достаточно рано. Поэтому перемешивается только 40% всех вершин графа. Данное преобразование требует дополнительной памяти для хранения перемешанного графа, зато мы получаем заметный прирост в производительности. Ниже представлен псевдокод ядра для процедуры BU с использованием перемешанного расположения элементов в памяти.
Параллельное ядро для процедуры BU:
__global__ void bu_align( ... )
{
idx = blockDim.x * blockIdx.x + threadIdx.x;
countQNext = 0; inlvl = 0;
for(i = idx; i < N; i += stride)
if (levels[i] == 0)
start_k = rowsIndices[i];
end_k = rowsIndices[i + N];
for(k = start_k; k < start_k + 32 * end_k; k += 32)
inlvl++;
vertex_id_t endk = endV[k];
if (levels[endk] == lvl - 1)
parents[i] = endk;
levels_out[i] = lvl;
countQNext++;
break;
atomicAdd(red_qnext, countQNext);
atomicAdd(red_lvl, inlvl);
}Анализ полученных результатов
Тестированные программы производилось сразу на четырех различных платформах: Intel Xeon Phi (Xeon KNL 7250), Intel x86 (Xeon E5 2699 v3), IBM Power8+ (Power 8+ s822lc) и GPU NVidia Tesla P100. Интересующие для сравнения характеристики данных устройств представлены в
таблице ниже.
Использовались следующие компиляторы. Для Intel Xeon E5 — gcc 5.3, для Intel KNL — icc v17, для IBM — gcc для Power архитектуры, для NVidia — CUDA 9.0.
| Вендор | Ядер / Потоков | Частота, ГГц | RAM, GB/s | Макс. TDP, Вт | Транз., млрд |
|---|---|---|---|---|---|
| Xeon KNL 7250 | 68 / 272 | 1.4 | 115 / 400 | 215 | ~8 |
| Xeon E5 2699 v3 | 18 / 36 | 2.3 | 68 | 145 | ~5.69 |
| Power 8+ s822lc | 10 / 80 | 3.5 | 205 | 270 | ~6 |
| Tesla P100 | 56 / 3584 | 1.4 | 40 / 700 | 300 | ~15.3 |
В последнее время производители все больше задумываются о пропускной способности памяти. Как следствие этому, появляются различные решение проблемы медленного доступа к оперативной памяти. Среди рассматриваемых платформ, две имеют двухуровневую структуру оперативной памяти.
Первая из них — Intel KNL, содержит быструю память на кристалле, скорость доступа к которой порядка 400 ГБ/с, и более медленную привычную нам DDR4, скорость доступа к которой не более 115 ГБ/с. Быстрая память имеет достаточно маленький размер — всего 16ГБ, в то время как обычная память может быть до 384 ГБ. На тестируемом сервере было установлено 96 ГБ памяти. Вторая платформа с гибридным решением — Power + NVidia Tesla. Данное решение базируется на новой технологии NVlink, которая позволяет иметь доступ к обычной памяти на скорости 40 ГБ/с, в то время как доступ к быстрой памяти осуществляется на скорости 700 ГБ/с. Количество быстрой памяти такое же, как и в Intel KNL — 16ГБ.
Данные решения схожи с точки зрения организации — имеется быстрая память маленького размера, и медленная память большого размера. Сценарий использования двухуровневой памяти при обработки больших графов очевиден: быстрая память используется для хранения результата и промежуточных массивов, размеры которых достаточно малы по сравнению с входными данным, а исходный граф читается из медленной памяти.
С точки зрения реализации пользователю доступны следующие средства. Для Intel KNL достаточно использовать другие функции выделения памяти — hbm_malloc, вместо привычного malloc. Если программа использовала операторы malloc, то достаточно объявить один define для того, чтобы использовать данную возможность. Для NVidia Tesla необходимо использовать также другие функции выделения памяти — вместо cudaMalloc использовать cudaMallocHost. Данные модификации кода являются достаточными и не требуют каких-либо модификаций в вычислительной части программы.
Эксперименты проводились для графов разного размера, начиная от 225 (4 ГБ) и заканчивая 230 (128 ГБ). Средняя степень связности и тип графа брались из генератора графа для рейтинга Graph500. Данный генератор создает графы Кронекера со средней степенью связности 16 и коэффициентами A = 0.57, B = 0.19, C = 0.19.
Данного вида графы используются всеми участниками таблицы рейтинга, что позволяет корректно сравнивать реализации между собой. Значение производительности считается по метрике TEPS для таблицы Graph500 и TEPS / w для таблицы GreenGraph500. Для вычисления данной характеристики выполняется 64 запуска алгоритма BFS из разных стартовых вершин и берется среднее значение. Для вычисления потребления алгоритма берется текущее потребление системы в момент работы алгоритма с учетом потребления оперативной памяти.
Следующая таблица иллюстрирует полученную производительность в GTEPS на всех тестируемых графах. В таблице указываются два значения — минимальная / максимальная достигнутая производительность на каждом из графов. Также в случае использования Intel KNL были получены результаты выполнения алгоритма при использовании только памяти DDR4. К сожалению, даже при использовании всех алгоритмов сжатия данных, не удалось запустить на предоставленном сервере граф с 230 вершинами на Intel KNL. Но учитывая стабильность работы Intel процессоров и технологичность Intel компиляторов, можно предположить, что производительность не изменится при увеличении размера графа (как это можно видеть для Intel Xeon E5).
Полученная производительность в GTEPS:
| Граф: | 225 | 226 | 227 | 228 | 229 | 230 |
|---|---|---|---|---|---|---|
| KNL 7250 | 10.7/30.6 | 12.9/41 | 8.4/43.3 | 4.6/40.2 | 6.2/42.6 | N/A |
| KNL 7250 DDR4 | 6.7/25.2 | 4.3/27 | 4.9/28.4 | 5.7/31.6 | 10.8/38.8 | N/A |
| E5 2699 v3 | 11/16.5 | 11.8/17.3 | 12.7/18.5 | 13.1/18.3 | 12.1/18.0 | 12.4/21.1 |
| P8+ s822lc | 8.8/22.5 | 9.02/23.3 | 7.98/23.4 | 10.4/23.7 | 10.1/24.6 | 7.59/14.8 |
| Tesla P100 | 41/282 | 99/333 | 34/324 | 50/274 | 7.2/61 | 6.5/52 |
На графике ниже отображена средняя производительность протестированных платформ. Можно заметить, что Power 8+ показал не очень хорошую стабильность при переходе с графа размером 64 ГБ на 128 ГБ. Возможно, это связано с тем, что использовался двух сокетный узел из двух аналогичных процессоров, причем у каждого процессора было по 128 ГБ памяти. И при обработке большего графа часть данных размещалось в памяти, не принадлежащей сокету. На графике также не отображена производительность Tesla P100 на более маленьких графах, так как разница между самым быстрым ЦПУ устройством и ГПУ составляет примерно 10 раз. Данное ускорение резко сокращается, когда графы становятся настолько большими, что не помещаются в кэш и доступ к графу осуществляется через NVlink. Но, несмотря на данное ограничение, производительность ГПУ все равно остается больше всех ЦПУ устройств. Такое поведение объясняется тем, что CUDA позволяет лучше контролировать вычисления и доступ к памяти, а также лучшей приспособленностью графических процессоров к параллельным вычислениям.
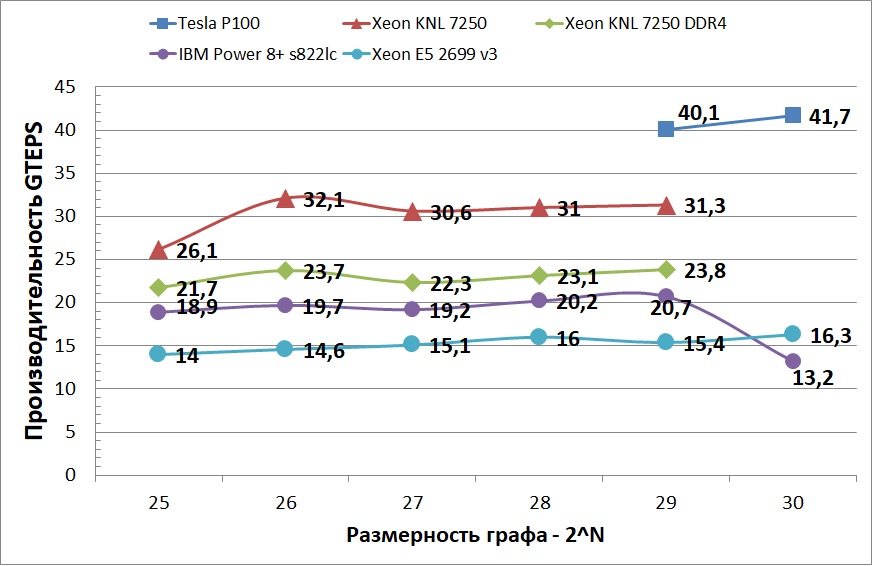
Таблица ниже иллюстрирует полученную производительность в GTEPS /w на всех тестируемых графах. В таблице указываются среднее энергопотребление при средней достигнутой производительности на каждом из графов. Резкое падение производительности и энергоэффективности при переходе с графа 228 на граф 229 на NVidia Tesla P100 объясняется тем, что быстрой памяти не хватает, чтобы поместить выровненную часть графа, к которой осуществляется наиболее частый доступ. В случае использования большего количества памяти (например, 32 ГБ) и увеличенного канала связи с ЦПУ NVlink 2.0 можно существенно повысить эффективность обработки графов большого размера.
Полученная энергоэффективность в MTEPS / w:
| Размер графа | 225 | 226 | 227 | 228 | 229 | 230 |
|---|---|---|---|---|---|---|
| KNL 7250 | 121.4 | 149.3 | 142.33 | 136.56 | 130.96 | N/A |
| E5 2699 v3 | 95.56 | 98.65 | 100 | 101.9 | 91.12 | 84.46 |
| P8+ s822lc | 93.8 | 97.04 | 93.2 | 95.28 | 92.41 | 53.23 |
| Tesla P100 | 1228.57 | 1165.71 | 1235.96 | 1016.57 | 195.61 | 177.45 |
Ну и напоследок
В результате проделанной работы были реализованы два параллельных алгоритма BFS для ЦПУ подобных систем и для ГПУ. Было выполнено исследование производительности и энергоэффективности реализованных алгоритмов на различных платформах, таких как IBM Power8+, Intel x86, Intel Xeon Phi (KNL) и NVidia Tesla P100. Данные платформы имеют различные архитектурные особенности. Несмотря на это, первые три из них очень похожи по строению. Благодаря этому на этих платформах можно запускать OpenMP приложения без каких-либо существенных изменений. Наоборот, архитектура ГПУ сильно отличается от ЦПУ подобных платформ и использует другую концепцию для реализации вычислительного кода — архитектуру CUDA.
Были рассмотрены графы, которые получаются после генератора для рейтинга Graph500. Была исследована производительность каждой из архитектур на двух классах данных. К первому классу относятся графы, которые помещаются в наиболее быструю память вычислителя. Ко второму классу относятся большие графы, которые нельзя поместить в быструю память целиком. Для демонстрации энергоэффективности использовались метрики GreenGraph500. Минимальный граф, который учитывается в рейтинге GreenGraph500 в классе больших данных, содержит в себе 230 вершин и 234 ребер и занимает в исходном виде 128 ГБ памяти. В классе же малых данных допускается граф любого размера до 230 вершин и 234 ребер, причем в качестве результата принимается наиболее большой граф, который удалось вместить в память.
На данный момент среди всех одноузловых систем в рейтинге Graph500 и GreenGraph500 полученная реализация на NVidia Tesla P100 занимает лидирующие позиции как в классе малых данных (с производительностью 220 GTEPS и эффективностью 1235.96 MTEPS/w), так и в классе больших данных (с производительностью 41.7 GTEPS и эффективностью 177.45 MTEPS/w). Такая высокая энергоэффективность и скорость работы на больших графах была достигнута благодаря новой технологии NVLink, которая связывает ГПУ и ЦПУ между собой и доступна на данный момент только в серверах компании IBM с ЦПУ Power8+.
В дальнейшем планируется исследовать возможность выполнения данного алгоритма на новой архитектуре NVidia Volta с использованием улучшенной технологии NVlink 2.0, а также планируется исследовать параллельную реализацию на нескольких ГПУ.
[1] E.F. Moore. The shortest path through a maze. In Int. Symp. on Th.
of Switching, pp. 285–292, 1959
[2] Cormen, T., Leiserson, C., Rivest, R.: Introduction to Algorithms. MIT Press,
Cambridge (1990)
[3] Edmonds, J., Karp, R.M.: Theoretical improvements in algorithmic efficiency for
network flow problems. Journal of the ACM 19(2), 248–264 (1972)
[4] Brandes, U.: A Faster Algorithm for Betweenness Centrality. J. Math. Sociol. 25(2),
163–177 (2001)
[5] Frasca, M., Madduri, K., Raghavan, P.: NUMA-Aware Graph Mining Techniques
for Performance and Energy Efficiency. In: Proc. ACM/IEEE Int. Conf. High Performance
Computing, Networking, Storage and Analysis (SC 2012), pp. 1–11. IEEE
Computer Society (2012)
[6] Girvan, M., Newman, M.E.J.: Community structure in social and biological networks.
Proc. Natl. Acad. Sci. USA 99, 7821–7826 (2002)
[7] D. A. Bader and K. Madduri. Designing multithreaded algorithms for
breadth-first search and st-connectivity on the Cray MTA-2. In ICPP,
pp. 523–530, 2006.
[8] R.E. Korf and P. Schultze. Large-scale parallel breadth-first search.
In AAAI, pp. 1380–1385, 2005.
[9] A. Yoo, E. Chow, K. Henderson, W. McLendon, B. Hendrickson, and
U. Catalyurek. A scalable distributed parallel breadth-first search
algorithm on BlueGene/L. In SC ’05, p. 25, 2005.
[10] Y. Zhang and E.A. Hansen. Parallel breadth-first heuristic search on a shared-memory architecture. In AAAI Workshop on Heuristic
Search, Memory-Based Heuristics and Their Applications, 2006.
[11] Yasui Y., Fujisawa K., Sato Y. (2014) Fast and Energy-efficient Breadth-First Search on a Single NUMA System. In: Kunkel J.M., Ludwig T., Meuer H.W. (eds) Supercomputing. ISC 2014. Lecture Notes in Computer Science, vol 8488. Springer, Cham
[12] Hiragushi T., Takahashi D. (2013) Efficient Hybrid Breadth-First Search on GPUs. In: Aversa R., Kolodziej J., Zhang J., Amato F., Fortino G. (eds) Algorithms and Architectures for Parallel Processing. ICA3PP 2013. Lecture Notes in Computer Science, vol 8286. Springer, Cham
[13] Merrill, D., Garland, M., Grimshaw, A.: Scalable GPU graph traversal. In: Proc. 17th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming (PPoPP 2012), pp. 117–128 (2012)


ZaMaZaN4iK
Шикарный материал. Спасибо большое.