
Перевод блога O Tannenbaum Майкла Тротта, директора Wolfram|Alpha.
В этом ноутбуке описывается, как создать анимацию украшенной елки, которая перемещает свои ветви синхронизированно с голосами музыки немецкой песни O Tannenbaum 16-го века (английская версия — O Christmas Tree). Одна выделенная ветвь дерева будет действовать как дирижер, а свеча будет дирижёрской палочкой. Это делает анимацию интересной во всех куплетах. Мы также добавим немного снега и несколько веселых движений дерева во второй половине песни. Чтобы увидеть окончательный дизайн, просмотрите это видео на YouTube:

Я реализую анимацию с помощью следующих этапов:
- Построить елку с изогнутыми ветвями, где ветви можно перемещать плавно вверх, вниз, влево и вправо.
- Добавить украшения (цветные шарики, пятиконечные звезды) и свечи разного цвета к ветвям. Позволить украшениям перемещаться относительно окончаниям веток.
- Преобразовать 4 голоса музыки в 2D-движение на основе частот звука. Смоделировать движения дирижера синхронизированными с музыкой.
- Моделировать движения украшений в виде вынужденного сферического маятника. Учет трения орнаментов с использованием диссипативной функции Рэлея.
- Добавить снег для белого рождества.
- Создать анимацию веток по отношению к музыке.
Особая благодарность моему коллеге Эндрю Штайхачеру за выбор и анализ музыки, чтобы получить данные для движения дерева (ниже раздел «От музыки к движениям»). И благодаря Эми Янг для превращения анимационных кадров и музыки в один видеоклип.
Создание елки
Параметры дерева
Размеры дерева, общая форма дерева и количество ветвей. Названия переменных делают их смысл очевидным.
(* radial branch count *)
radialBranchCount = 3;
(* vertical branch count *)
verticalBranchCount = 5;
(* tree height *)
treeHeight = 12;
(* tree width *)
treeWidth = 6;
(* plot points for the B-spline surfaces forming the branches *)
{?, ?} = {6, 8}; Цвета ствола и ветвей.
stemColor = Directive[Darker[Brown], Lighting -> "Neutral", Specularity[Brown, 20]];
branchTopColor = RGBColor[0., 0.6, 0.6];
branchBottomColor = RGBColor[0., 0.4, 0.4];
branchSideColor = RGBColor[0.4, 0.8, 0.];Построение движущейся ветки дерева
Каждая ветвь имеет поперечное сечение прямоугольника с изменяющейся размерностью (в зависимости от расстояния от ствола). Кончик ветки должен слегка указывать вверх, чтобы иметь знакомый вид елки. В его самом широком размере ветвь лежит близко к конусу (стволу). Переменная ? определяет вверх-вниз и переменная ? лево-право положения кончика ветки. Я строю ветку с четырех поверхностей B-сплайна (сверху, снизу, слева, справа), чтобы иметь гладкий вид с небольшим количеством точек, определяющих поверхность.
branchTopBottom[
tp_, {hb_, ht_}, {?1_, ?2_}, {rb_, rt_},
R_, {?_, ?_}] :=
Module[{A = -0.6, ? = 1/2, ?m, Pm, dirR,
dir?, r, P1, P, \[ScriptN], \[ScriptP], x,
y, ?, ?, ?, \[ScriptH]s, \[ScriptH]},
?m = Mean[{?1, ?2}];
Pm = R {Cos[?m], Sin[?m]};
dirR = 1. {Cos[?m], Sin[?m]};
dir? = Reverse[dirR] {-1, 1};
r = If[tp == "top", rt, rb];
(* move cross section radially away from the stem and contract it *)
Table[P1 = {r Cos[?], r Sin[?]};
Table[P = P1 + s/? (Pm - P1);
\[ScriptN] = dir?.P; \[ScriptP] = dirR.P;
{x,
y} = \[ScriptN] Cos[
s/? Pi/2]^2 dir? + \[ScriptP] dirR;
? = ?*
1. s/? Abs[?2 - ?1]/
radialBranchCount;
? = {{Cos[?],
Sin[?]}, {-Sin[?], Cos[?]}};
{x, y} = ?.{x, y};
? = R s/?;
\[ScriptH]s = {ht,
hb} + {? (A R (R - ?) - (hb - ht) (? -
1) ?), (ht - hb) ?^2 ?}/R^2;
\[ScriptH] =
If[tp == "top", \[ScriptH]s[[1]], \[ScriptH]s[[2]]] ;
{x, y, \[ScriptH] + ? s/? (ht - hb)},
{s, 0, ?}],
{?, ?1, ?2, (?2 - ?1)/?}] // N
]Радиус на высоте h представляет собой только линейную интерполяцию максимального радиуса ствола и радиуса 0 в верхней части.
stemRadius[h_, H_] := (H - h)/HСтороны ветки — это только соединительные элементы между верхней и нижней поверхностями.
branchOnStem[{{hb_, ht_}, {?1_, ?2_},
R_}, {?_, ?_}] :=
Module[{tBranch, bBranch, sideBranches},
{bBranch, tBranch} =
Table[branchTopBottom[p, {hb, ht}, {?1, ?2},
stemRadius[{hb, ht}, treeHeight],
R, {?, ?}], {p, {"top", "bottom"}}];
sideBranches =
Table[BSplineSurface[{tBranch[[j]],
bBranch[[j]]}], {j, {1, -1}}];
{branchTopColor, BSplineSurface[tBranch],
branchBottomColor, BSplineSurface[bBranch],
branchSideColor, sideBranches}
]Для последующего использования давайте определим функцию только для позиции конца ветки.
branchOnStemEndPoint[ {{hb_, ht_}, {?1_, ?2_},
R_}, {?_, ?_}] :=
Module[{A = -0.6, ? = 1/2, Pm, dirR, dir?,
P, \[ScriptN], \[ScriptP], x,
y, ?, ?, \[ScriptH]s, \[ScriptH],
? = ?1, ?m =
Mean[{?1, ?2}]},
Pm = R {Cos[?m], Sin[?m]};
dirR = {Cos[?m], Sin[?m]};
{x, y} = dirR.Pm dirR;
? =
1. ? Abs[?2 - ?1]/radialBranchCount;
{x, y} = {{Cos[?], Sin[?]}, {-Sin[?],
Cos[?]}}.{x, y};
\[ScriptH]s = {ht, hb} + (ht - hb) {? - 1., 1};
{x, y, \[ScriptH]s[[1]] + ? (ht - hb)} ]Интерактивная демонстрация, позволяющая ветке и ее окончанию двигаться как функция от {?, ?}.
Manipulate[
Graphics3D[{branchOnStem[{{0, 1}, {Pi/2 - 1/2, Pi/2 + 1/2},
1 + ?}, ??],
Red,
Sphere[branchOnStemEndPoint[{{0, 1}, {Pi/2 - 1/2, Pi/2 + 1/2},
1 + ?}, ??], 0.05]},
PlotRange -> {{-2, 2}, {0, 4}, {-1, 2}},
ViewPoint -> {3.17, 0.85, 0.79}],
{{?, 1.6, "branch length"}, 0, 2, ImageSize -> Small},
{{??, {0, 0},
"branch\nleft/right\nup/down"}, {-1, -1}, {1, 1}},
ControlPlacement -> Left, SaveDefinitions -> True]
Добавление ветвей к стволу
Ствол — это всего лишь конус, вершиной которого является вершина дерева.
stem = Cone[{{0, 0, 0}, {0, 0, treeHeight}}, 1];Размеры ветвей уменьшаются с высотой, становясь геометрически меньше. Общее количество всех уровней ветвей равно высоте дерева минус часть шага внизу.
heightList1 =
Module[{? = 0.8, hs, sol},
hs = Prepend[Table[C ?^k, {k, 0, verticalBranchCount - 1}],
0];
sol = Solve[Total[hs] == 10, C, Reals];
Accumulate[hs /. sol[[1]]]]{0, 2.97477, 5.35459, 7.25845, 8.78153, 10.}
treeWidthOfHeight[h_] := treeWidth (treeHeight - h)/treeHeightВетви плотно прилегают к стволу, без промежутков между ними.
Graphics3D[{{stemColor, stem},
{Darker[Green],
Table[Table[
branchOnStem[{2 +
heightList1[[{j, j + 1}]], {k , k + 1} 2 Pi/
radialBranchCount ,
treeWidthOfHeight[Mean[heightList1[[{j, j + 1}]]]]}, {0,
0}], {k, 0, 1}] ,
{j, 1, verticalBranchCount}]}},
ViewPoint -> {2.48, -2.28, 0.28}]

Graphics3D[{{stemColor, stem},
{Darker[Green],
Table[Table[
branchOnStem[{2 +
heightList1[[{j, j + 1}]], {k , k + 1} 2 Pi/
radialBranchCount ,
treeWidthOfHeight[Mean[heightList1[[{j, j + 1}]]]]}, {0,
0}], {k, 0, radialBranchCount - 1}] ,
{j, 1, verticalBranchCount}]}},
ViewPoint -> {2.48, -2.28, 0.28}]
Можно переместить ветки, чтобы получить более реалистичную форму дерева. Это то дерево, которое я буду использовать в последующем. Изменить параметры дерева и использовать другое дерево довольно просто.
heightList2 = {2/3, 1/3}.# & /@ Partition[heightList1, 2, 1];
Graphics3D[{{Darker[Brown], stem},
{EdgeForm[],
Table[
Table[branchOnStem[ {2 +
heightList1[[{j, j + 1}]], {k , k + 1} 2 Pi/
radialBranchCount ,
treeWidthOfHeight[Mean[heightList1[[{j, j + 1}]]]]}, {0,
0}], {k, 0, radialBranchCount - 1}] ,
{j, 1, verticalBranchCount}],
Table[Table[
branchOnStem[{2 +
heightList2[[{j, j + 1}]], {k , k + 1} 2 Pi/
radialBranchCount + Pi/radialBranchCount,
treeWidthOfHeight[Mean[heightList2[[{j, j + 1}]]]]}, {0,
0}], {k, 0, radialBranchCount - 1}] ,
{j, 1, verticalBranchCount - 1}]}},
ViewPoint -> {2.48, -2.28, 0.28}]
Можно было бы легко сделать деревья еще плотнее с большим количеством ветвей.
Graphics3D[{{Darker[Brown], stem},
{EdgeForm[],
Table[Table[branchOnStem[ {2 + heightList1[[{j, j + 1}]],
{k , k + 1} 2 Pi/(2 radialBranchCount) ,
treeWidthOfHeight[Mean[heightList1[[{j, j + 1}]]]]}, {0,
0}], {k, 0, (2 radialBranchCount) - 1}] , {j, 1,
verticalBranchCount}],
Table[Table[branchOnStem[{2 + heightList2[[{j, j + 1}]],
{k , k + 1} 2 Pi/(2 radialBranchCount) +
Pi/(2 radialBranchCount),
treeWidthOfHeight[Mean[heightList2[[{j, j + 1}]]]]}, {0,
0}], {k, 0, 2 radialBranchCount - 1}] ,
{j, 1, verticalBranchCount - 1}]}},
ViewPoint -> {2.48, -2.28, 0.28}]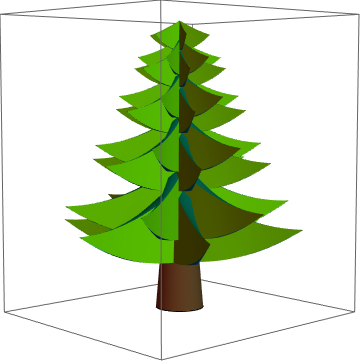
Украшение дерева
Теперь давайте построим несколько украшений, чтобы построить красиво наряженную елку. Я добавлю блестящие шарики, пятиконечные звезды и свечи. Я рекомендую оригинальные шары Тюрингии Лауша для вашей елки. (Вы можете найти их здесь)
Украшения, свечи и верхушка
Цветные шары
На каждом дереве должны быть какие-то блестящие стеклянные сферы, игрушки.
coloredBall[p_, size_, color_, {?_, ?_}] :=
Module[{\[ScriptD] = {Cos[?] Sin[?],
Sin[?] Sin[?], -Cos[?]}},
{EdgeForm[], GrayLevel[0.4], Specularity[Yellow, 20],
Cylinder[{p, p + 1.5 size \[ScriptD]}, 0.02 size ],
color, Specularity[Yellow, 10],
Sphere[p + (1.5 size + 0.6 size) \[ScriptD] , 0.6 size]
}]
Graphics3D[{coloredBall[{1, 2, 3}, 1, Red, {0, 0}],
coloredBall[{3, 2, 3}, 1, Darker[Blue], {1, 0.2}]}, Axes -> True]
branchOnStemWithBall[{{hb_, ht_}, {?1_, ?2_},
R_}, {?_, ?_}, color_, {?_, ?_}] :=
{branchOnStem[{{hb, ht}, {?1, ?2},
R}, {?, ?}] ,
coloredBall[
branchOnStemEndPoint[{{hb, ht}, {?1, ?2},
R}, {?, ?}], 0.45 (ht - hb)/2,
color, {?, ?}]}Вот ветка с игрушкой. Переменные {?, ?} позволяют изменить положение шара относительно кончика ветки.
Manipulate[
Graphics3D[{branchOnStemWithBall[{{0, 1}, {Pi/2 - 1/2, Pi/2 + 1/2},
1 + ?}, ??, Red, ??]},
PlotRange -> {{-2, 2}, {0, 4}, {-2, 2}},
ViewPoint -> {3.17, 0.85, 0.79}],
{{?, 1.6, "branch length"}, 0, 2, ImageSize -> Small},
{{??, {0.6, 0.26},
"branch\nleft/right\nup/down"}, {-1, -1}, {1, 1}},
{{??, {2.57, 1.88}, "ball angles"}, {0, -Pi}, {Pi, Pi}},
ControlPlacement -> Left, SaveDefinitions -> True]
Вот дерево с шарами весящими в основном прямо вниз. Я буду использовать случайные цвета для шаров.
Graphics3D[{{Darker[Brown],
stem}, {Table[
Table[branchOnStemWithBall[{2 +
heightList1[[{j, j + 1}]], {k , k + 1} 2 Pi/
radialBranchCount ,
treeWidthOfHeight[Mean[heightList1[[{j, j + 1}]]]]}, {0, 0},
RandomColor[], {0, 0}], {k, 0,
radialBranchCount - 1}] ,
{j, 1, verticalBranchCount}]
}}, ViewPoint -> {2.48, -2.28, 0.28}, Axes -> True]
Дерево с шарами в случайных направлениях. Если позже ветви будут перемещены, то мы вычислим естественные движения (что означает решение соответствующих уравнений движения) шаров.
Graphics3D[{{Darker[Brown],
stem}, {Table[
Table[branchOnStemWithBall[{2 +
heightList1[[{j, j + 1}]], {k , k + 1} 2 Pi/
radialBranchCount ,
treeWidthOfHeight[Mean[heightList1[[{j, j + 1}]]]]}, {0, 0},
RandomColor[], {RandomReal[{-Pi, Pi}],
RandomReal[{0, Pi}]}], {k, 0, radialBranchCount - 1}] ,
{j, 1, verticalBranchCount}]}},
ViewPoint -> {2.48, -2.28, 0.28}, Axes -> True]
Пятиконечные звезды
Сейчас построим несколько пятиконечных звезд. Поскольку этот орнамент не имеет вращательной симметрии, я допущу угол ориентации относительно нити на которой он висит.
coloredFiveStar[p_, size_, dir_,
color_, ?_, {?_, ?_}] :=
Module[{\[ScriptD] = {Cos[?] Sin[?],
Sin[?] Sin[?], -Cos[?]}, points, P1, P2, d1,
d2, d3, dP, dP2},
d2 = Normalize[dir - dir.\[ScriptD] \[ScriptD]];
d3 = Cross[\[ScriptD], d2];
{EdgeForm[], GrayLevel[0.4], Specularity[Pink, 20],
Cylinder[{p, p + (1.5 size + 0.6 size) \[ScriptD]}, 0.02 size ],
color, Specularity[Hue[.125], 5],
dP = Sin[?] d2 + Cos[?] d3;
dP2 = Cross[\[ScriptD], dP];
points =
Table[p + (1.5 size + 0.6 size) \[ScriptD] +
size If[EvenQ[j], 1, 1/2] *
(Cos[j 2 Pi/10 ] \[ScriptD] +
Sin[j 2 Pi/10] dP), {j, 0, 10}];
P1 = p + (1.5 size + 0.6 size) \[ScriptD] + size/3 dP2;
P2 = p + (1.5 size + 0.6 size) \[ScriptD] - size/3 dP2;
{P1, P2} = (p + (1.5 size + 0.6 size) \[ScriptD] + # size/
3 dP2) & /@ {+1, -1};
Polygon[
Join @@ (Function[a,
Append[#, a] & /@ Partition[points, 2, 1]] /@ {P1, P2})]
}]
Graphics3D[{coloredFiveStar[{1, 2, 3}, 0.2, {0, -1, 0}, Darker[Red],
0, {0, 0}],
coloredFiveStar[{1.5, 2, 3}, 0.2, {0, -1, 0}, Darker[Purple],
Pi/3, {1, 0.4}]}]
branchOnStemWithFiveStar[{{hb_, ht_}, {?1_, ?2_},
R_}, {?_, ?_},
color_, ?_, {?_, ?_}] :=
Module[{dir =
Append[Normalize[
Mean[{{Cos[?1],
Sin[?1]}, {Cos[?2],
Sin[?2]}}]], 0]},
{branchOnStem[{{hb, ht}, {?1, ?2},
R}, {?, ?}] ,
coloredFiveStar[
branchOnStemEndPoint[{{hb, ht}, {?1, ?2},
R}, {?, ?}], 0.4 (ht - hb)/2, dir,
color, ?, {?, ?}]} ]Елка украшена пятиконечными звездами.
Graphics3D[{{Darker[Brown],
stem}, {Table[
Table[branchOnStemWithFiveStar[{2 +
heightList1[[{j, j + 1}]], {k , k + 1} 2 Pi/
radialBranchCount ,
treeWidthOfHeight[Mean[heightList1[[{j, j + 1}]]]]}, {0, 0},
RandomColor[],
RandomReal[{-Pi, Pi}], {RandomReal[{-Pi, Pi}],
RandomReal[0.1 {-1, 1}]}], {k, 0, radialBranchCount - 1}] ,
{j, 1, verticalBranchCount}]
}}, ViewPoint -> {2.48, -2.28, 0.28}, Axes -> True]
Свечи
Построим их начиная с ножки, которая прикрепляется к окончаниям веток, с воскоподобным телом, почерневшем фитилем и огнем. Чтобы облегчить анимацию и избежать пожара, я буду использовать электрические свечи, чтобы пламя не изменялось, когда двигаются ветви.
flamePoints =
Table[{0.2 Sin[Pi z]^2 Cos[?],
0.2 Sin[Pi z]^2 Sin[?], z}, {z, 0, 1,
1/1/12}, {?, Pi/2, 5/2 Pi, 2 Pi/24}]
litCandle[p_, size_, color_] :=
{EdgeForm[], color,
Cylinder[{p + {0, 0, size 0.001}, p + {0, 0, size 0.5}}, size 0.04],
GrayLevel[0.1], Specularity[Orange, 20],
Cylinder[{p, p + {0, 0, size 0.05}}, size 0.06],
Black, Glow[Black],
Cylinder[{ p + {0, 0, size 0.5}, p + {0, 0, size 0.5 + 0.05 size}},
size 0.008],
Glow[Orange], Specularity[Hue[.125], 5],
BSplineSurface[
Map[(p + {0, 0, size 0.5} + 0.3 size #) &, flamePoints, {2}],
SplineClosed -> {True, False}]
}Белая и красная свечи.
Graphics3D[{litCandle[{0, 0, 0}, 1,
Directive[White, Glow[GrayLevel[0.3]], Specularity[Yellow, 20]]],
litCandle[{0.5, 0, 0}, 1,
Directive[Red, Glow[GrayLevel[0.1]], Specularity[Yellow, 20]]]}]
Позже я буду использовать удлиненную ветку со свечой, чтобы она была дирижером, поэтому я позволю свечи наклониться от ветви.
branchOnStemWithCandle[{{hb_, ht_}, {?1_, ?2_},
R_}, {?_, ?_}, color_, ?_] :=
{branchOnStem[{{hb, ht}, {?1, ?2},
R}, {?, ?}] ,
If[? == 0,
litCandle[
branchOnStemEndPoint[{{hb, ht}, {?1, ?2},
0.98 R}, {?, ?}], 0.66 (ht - hb) , color],
Module[{P =
branchOnStemEndPoint[{{hb, ht}, {?1, ?2},
0.98 R}, {?, ?}], dir},
dir = Append[Reverse[Take[P, 2]] {-1, 1}, 0];
Rotate[
litCandle[
branchOnStemEndPoint[{{hb, ht}, {?1, ?2},
0.98 R}, {?, ?}], 0.66 (ht - hb) ,
color], ?, dir, P]]]}
Manipulate[
Graphics3D[{branchOnStemWithCandle[{{0, 1}, {Pi/2 - 1/2, Pi/2 + 1/2},
1 + ?}, ??, Red, ?]},
PlotRange -> {{-2, 2}, {0, 4}, {-2, 2}},
ViewPoint -> {3.17, 0.85, 0.79}],
{{?, 1.6, "branch length"}, 0, 2, ImageSize -> Small},
{{??, {0, 0},
"branch\nleft/right\nup/down"}, {-1, -1}, {1, 1}},
{{?, Pi/4, "candle angle"}, -Pi, Pi},
ControlPlacement -> Left, SaveDefinitions -> True]И вот ель со свечой на каждой ветке.
Graphics3D[{{Darker[Brown],
stem}, {Table[
Table[branchOnStemWithCandle[{2 +
heightList1[[{j, j + 1}]], {k , k + 1} 2 Pi/
radialBranchCount ,
treeWidthOfHeight[Mean[heightList1[[{j, j + 1}]]]]}, {0, 0},
White, 0], {k, 0,
radialBranchCount - 1}] ,
{j, 1, verticalBranchCount}]
}}, ViewPoint -> {2.48, -2.28, 0.28}, Axes -> True]
Верхушка елки
Для полной радости я добавляю вращающийся спайки на верху.
spikey = Cases[
N@Entity["Polyhedron", "RhombicHexecontahedron"][
"Image"], _GraphicsComplex, ?][[1]];
top = {Gray, Specularity[Red, 25],
Cone[{{0, 0, 0.9 treeHeight}, {0, 0, 1.08 treeHeight}},
treeWidth/240],
Orange, EdgeForm[Darker[Orange]], Specularity[Hue[.125], 5],
MapAt[((0.24 # + {0, 0, 1.08 treeHeight}) & /@ #) &, spikey, 1]
}
Graphics3D[{{Darker[Brown], stem},
{Table[
Table[branchOnStem[{2 +
heightList1[[{j, j + 1}]], {k , k + 1} 2 Pi/
radialBranchCount ,
treeWidthOfHeight[Mean[heightList1[[{j, j + 1}]]]]}, {0,
0} ], {k, 0, radialBranchCount - 1}] ,
{j, 1, verticalBranchCount}],
top}}, ViewPoint -> {2.48, -2.28, 0.28}, Axes -> True]
Украшение дерева
Мы выделим одну ветку в качестве дирижера. Оставшиеся ветки мы случайным образом разделим на четыре группы и украсим их игрушками двух цветов, пятиконечными звездами и свечами.
Теперь давайте добавим украшение или свечу на каждую ветку дерева. Я буду использовать вышеупомянутое дерево с 27 ветками. Я начинаю ветки по высоте на стебле и азимутальным углом.
allBranches =
Flatten[Riffle[
Table[Table[{2 +
heightList1[[{j, j + 1}]], {k , k + 1} 2. Pi/
radialBranchCount ,
treeWidthOfHeight[Mean[heightList1[[{j, j + 1}]]]]}, {k, 0,
radialBranchCount - 1}] ,
{j, 1, verticalBranchCount}],
Table[Table[{2 +
heightList2[[{j, j + 1}]], {k , k + 1} 2. Pi/
radialBranchCount + Pi/radialBranchCount,
treeWidthOfHeight[Mean[heightList2[[{j, j + 1}]]]]}, {k, 0,
radialBranchCount - 1}] ,
{j, 1, verticalBranchCount - 1}]], 1]
Length[allBranches]27
Раскрасим ветки по порядку, начиная с красного внизу и до фиолетового на верху.
Graphics3D[{{Darker[Brown], stem},
MapIndexed[(branchOnStem[#1, {0, 0}] /. _RGBColor :>
Hue[#2[[1]]/36]) &, allBranches],
top}, ViewPoint -> {2, 1, -0.2}]
Разделим все ветки на 4 группы для голосов и одну для роли дирижера.
conductorBranch = 7;
SeedRandom[12];
voiceBranches = (Last /@ #) & /@
GroupBy[{RandomChoice[{1, 2, 3, 4}], #} & /@
Delete[Range[27], {conductorBranch}], First]<|1 -> {1, 4, 5, 6, 12, 18, 20}, 3 -> {2, 8, 10, 11, 14, 22, 23, 25}, 2 -> {3, 13, 15, 16, 21, 26}, 4 -> {9, 17, 19, 24, 27}|>
voiceBranches = <|1 -> {2, 9, 14, 17, 19, 24, 27},
2 -> {3, 13, 15, 16, 21, 26}, 3 -> {1, 4, 5, 12, 18, 20},
4 -> {6, 8, 10, 11, 22, 23, 25}|><|1 -> {2, 9, 14, 17, 19, 24, 27}, 2 -> {3, 13, 15, 16, 21, 26}, 3 -> {1, 4, 5, 12, 18, 20}, 4 -> {6, 8, 10, 11, 22, 23, 25}|>
Вот иллюстрация веток, окрашенных в соответствии с тем, какой голос они представляют.
Graphics3D[{{Darker[Brown], stem},
branchOnStem[#1, {0, 0}] & /@
allBranches[[voiceBranches[[1]]]] /. _RGBColor :> Yellow,
branchOnStem[#1, {0, 0}] & /@
allBranches[[voiceBranches[[2]]]] /. _RGBColor :> White,
branchOnStem[#1, {0, 0}] & /@
allBranches[[voiceBranches[[3]]]] /. _RGBColor :> LightBlue,
branchOnStem[#1, {0, 0}] & /@
allBranches[[voiceBranches[[4]]]] /. _RGBColor :> Pink,
branchOnStem[
allBranches[[conductorBranch]] {1, 1, 1.5}, {0,
0}] /. _RGBColor :> Red,
top}, ViewPoint -> {2, 1, -0.2}]
Завершенное дерево с расположением окончания веток в качестве параметров. Также позволим украшениям на кончиках веток сидеть под наклоном и быть разноцветными.
christmasTree[{{?1_, ?1_}, {?2_, ?2_}, {?3_, ?3_}, {?4_, ?4_}, {?c_, ?c_}},
{{?1_, ?1_}, {?2_, ?2_}, {?3_, ?3_}},
{colBall1_, colBall2_, col5Star_},
conductorEnhancementFactor : fc_,
conductorCandleAngle : ?c_, topRotationAngle : ?_] :=
{{Darker[Brown], stem},
branchOnStemWithBall[#, {?1, ?1},
colBall1, {?1, ?1}] & /@
allBranches[[voiceBranches[[1]]]],
branchOnStemWithBall[#, {?2, ?2},
colBall2, {?2, ?2}] & /@
allBranches[[voiceBranches[[2]]]],
branchOnStemWithFiveStar[#, {?3, ?3}, col5Star,
Pi/4, {?3, ?3}] & /@
allBranches[[voiceBranches[[3]]]],
branchOnStemWithCandle[#, {?4, ?4},
Directive[White, Glow[GrayLevel[0.3]], Specularity[Yellow, 20]],
0] & /@ allBranches[[voiceBranches[[4]]]],
branchOnStemWithCandle[
allBranches[[conductorBranch]] {1, 1,
1 + fc}, {?c, ?c},
Directive[Red, Glow[GrayLevel[0.1]],
Specularity[Yellow, 20]], ?c],
Rotate[top, ?, {0, 0, 1}]
};
Начальное положение всех ветвей и удлиненной ветки дирижера, где ее свеча наклонена.
Graphics3D[christmasTree[{{0, 0}, {0, 0}, {0, 0}, {0, 0}, {0, 0}},
{{0, 0}, {0,0}, {0, 0}}, {Red, Darker[Yellow], Pink}, 0.8, Pi/4, 0],
ImageSize -> 600, ViewPoint -> {3.06, 1.28, 0.27},
PlotRange -> {{-7, 7}, {-7, 7}, {0, 15}}]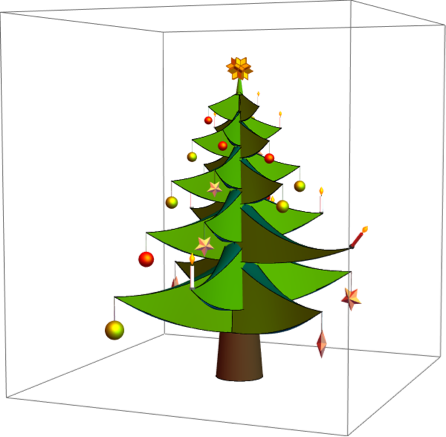
Три ели со всеми параметрами, выбранными случайным образом.
SeedRandom[1]
Table[Graphics3D[christmasTree[RandomReal[1.5 {-1, 1}, {5, 2}],
Table[{RandomReal[{-Pi, Pi}], RandomReal[{0, Pi}]}, 3],
RandomColor[3],
RandomReal[], RandomReal[Pi/2], 0], ImageSize -> 200,
ViewPoint -> {3.06, 1.28, 0.27},
PlotRange -> {{-7, 7}, {-7, 7}, {-2, 15}}], {3}] // Row
Следующие интерактивные демонстрации позволяют перемещать ветки, перемещать украшения вокруг окончаний веток и окрашивать украшения по вашему усмотрению.
Manipulate[
Graphics3D[
christmasTree[{??1, ??2, ??3, ??4, ??c},
{??1, ??2, ??3}, {col1, col2, col3},
l, ?c, ?],
ImageSize -> 400,
ViewPoint -> {2.61, 1.99, 0.80},
PlotRange -> {{-7, 7}, {-7, 7}, {-2, 15}}],
"conductor",
{{l, 0.6, "branch length"}, 0, 1, ImageSize -> Small},
{{?c, Pi/4, "candle angle"}, 0, Pi, ImageSize -> Small},
{{??c, {0, 0}, "movement"}, {-1, -1}, {1, 1},
ImageSize -> Small},
Delimiter,
"voice 1 (balls)",
Grid[{{"movement", "ornament"},
{Control[{{??1, {0, 0}, ""}, {-1, -1}, {1, 1},
ImageSize -> Small}],
Control[{{??1, {0, 0}, ""}, {-Pi, 0}, {Pi, Pi},
ImageSize -> Small}]}}],
{{col1, Red, ""}, Red, ImageSize -> Tiny},
Delimiter,
"voice 2 (balls)",
Grid[{{"movement", "ornament"},
{Control[{{??2, {0, 0}, ""}, {-1, -1}, {1, 1},
ImageSize -> Small}],
Control[{{??2, {0, 0}, ""}, {-Pi, 0}, {Pi, Pi},
ImageSize -> Small}]}}],
{{col2, Darker[Yellow], ""}, Red, ImageSize -> Tiny},
Delimiter,
"voice 3 (5-star)",
Grid[{{"movement", "ornament"},
{Control[{{??3, {0, 0}, ""}, {-1, -1}, {1, 1},
ImageSize -> Small}],
Control[{{??3, {0, 0}, ""}, {-Pi, 0}, {Pi, Pi},
ImageSize -> Small}]}}],
{{col3, Pink, ""}, Red, ImageSize -> Tiny},
Delimiter,
"voice 4 (white candles)",
Control[{{??4, {0, 0}, "movement"}, {-1, -1}, {1, 1},
ImageSize -> Small}],
Delimiter,
Delimiter,
{{?, 0, "top rotation"}, 0, 1, ImageSize -> Small},
ControlPlacement -> Left, SaveDefinitions -> True]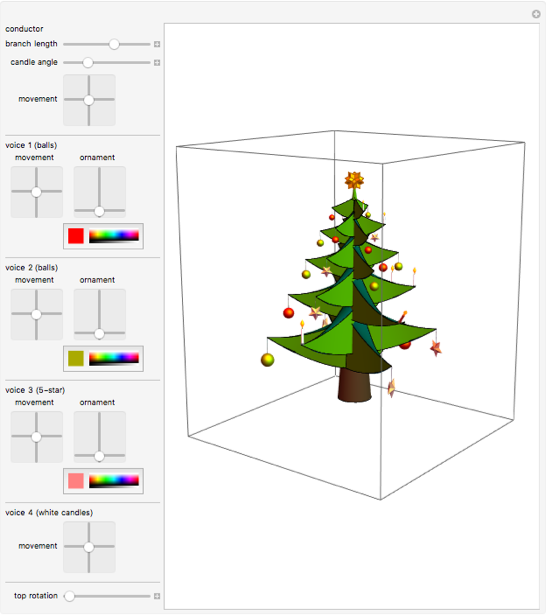
От музыки к движению
Итак, теперь, когда я закончил изготовлением параметризованной рождественской елки с подвижными ветками и украшениями, я должен заняться соотношением музыки к движениям веток (и, в свою очередь, украшений).
Получите 4 голоса как звук
Используйте MIDI-файл песни.

{ohTannenBaum // Head, ohTannenBaum // ByteCount}{Sound, 287816}
Извлеките 4 голоса.
voices = AssociationThread[{"Soprano", "Alto", "Tenor", "Bass"},
ImportString[
ExportString[ohTannenBaum, "MIDI"], {"MIDI", "SoundNotes"}]];
Sound[Take[#, 10]] & /@ voices
Голос в частоту
frequencyRules = <|"A1" -> 55., "A2" -> 110., "A3" -> 220.,
"A4" -> 440., "B1" -> 61.74, "B2" -> 123.5, "B3" -> 246.9,
"B4" -> 493.9, "C2" -> 65.41, "C3" -> 130.8, "C4" -> 261.6,
"C5" -> 523.3, "D2" -> 73.42, "D#4" -> 311.13, "D4" -> 293.7,
"D5" -> 587.3, "E2" -> 82.41, "E4" -> 329.6, "E5" -> 659.3,
"F#2" -> 92.50, "F#4" -> 370.0, "G2" -> 98.00, "G#4" -> 415.3,
"G4" -> 392.0|>;
{minf, maxf} = MinMax[frequencyRules]{55., 659.3}
Временной график первого голоса.
pw[t_] = Piecewise[{frequencyRules[#1], #2[[1]] <= t <= #2[[2]]} & @@@
voices[[1]]];
Plot[pw[t], {t, 0, 100}, PlotRange -> {200, All}, Filling -> Axis,
PlotLabel -> "Soprano",
Frame -> True, FrameLabel -> {"time in sec", "frequency in Hz"},
AxesOrigin -> {0, 200}]
Для представления частот в движениях я сглажу кривые.
spline = BSplineFunction[Table[{t, pw[t]}, {t, 0, 100, 0.5}],
SplineDegree -> 2]
ParametricPlot[spline[t], {t, 0, 100}, AspectRatio -> 0.5,
PlotPoints -> 1000]

tMax = 100;
Do[
With[{j = j},
pwf[j][t_] =
Piecewise[{frequencyRules[#1], #2[[1]] <= t <= #2[[2]]} & @@@
voices[[j]]];
splineFunction[j] =
BSplineFunction[Table[{t, pwf[j][t]}, {t, 0, 100, 0.5}],
SplineDegree -> 2];
voiceFunction[j][t_Real] :=
If[0 < t < tMax, splineFunction[j][t/tMax][[2]]/maxf, 0]],
{j, 4}]Частоты четырех голосов.
Plot[Evaluate[Reverse@Table[pwf[j][t], {j, 4}]], {t, 0, 100},
Frame -> True, FrameLabel -> {"time in sec", "frequency in Hz"},
AspectRatio -> 0.3]
Сглаженные масштабированные частоты четырех голосов.
Plot[Evaluate[Table[voiceFunction[j][t], {j, 4}]], {t, 0, 100},
Frame -> True, FrameLabel -> {"time in sec", "scaled frequency"},
AspectRatio -> 0.3]
Вот график (сглаженных) первых трех голосов в 3D.
ParametricPlot3D[{voiceFunction[1][t], voiceFunction[2][t],
voiceFunction[3][t]}, {t, 0, 100}, AspectRatio -> Automatic,
PlotPoints -> 1000, BoxRatios -> {1, 1, 1}]

Show[% /. Line[pts_] :> Tube[pts, 0.002],
Method -> {"TubePoints" -> 4}]
Получить закономерность колебания
Привязка к определенным фразам для создания всех отбиваний такта.
{firstBeat, secondBeat, lastBeat} =
voices["Soprano"][[{1, 2, -1}, 2, 1]]{1.33522, 2.00568, 98.7727}
anchorDataOChristmasTree = SequenceCases[
voices["Soprano"],
(* pattern for "O Christmas Tree, O Christmas Tree..." *)
{
SoundNote["D4", {pickupStart_, _}, "Trumpet", ___],
SoundNote["G4", {beatOne_, _}, "Trumpet", ___],
SoundNote["G4", {_, _}, "Trumpet", ___],
SoundNote["G4", {beatTwo_, _}, "Trumpet", ___],
SoundNote["A4", {beatThree_, _}, "Trumpet", ___],
SoundNote["B4", {beatFour_, _}, "Trumpet", ___],
SoundNote["B4", {_, _}, "Trumpet", ___],
SoundNote["B4", {beatFive_, _}, "Trumpet", ___]
} :> <|
"PhraseName" -> "O Christmas Tree",
"PickupBeat" -> pickupStart,
"TargetMeasureBeats" -> {beatOne, beatTwo, beatThree},
"BeatLength" ->
Mean@Differences[{pickupStart, beatOne, beatTwo, beatThree,
beatFour, beatFive}]
|>
];
anchorDataYourBoughsSoGreen = SequenceCases[
voices["Soprano"],
(* "Your boughs so green in summertime..." *)
{
SoundNote["D5", {pickupBeatAnd_, _}, "Trumpet", ___],
SoundNote["D5", {beatOne_, _}, "Trumpet", ___],
SoundNote["B4", {_, _}, "Trumpet", ___],
SoundNote["E5", {beatTwo_, _}, "Trumpet", ___],
SoundNote["D5", {beatThreeAnd_, _}, "Trumpet", ___],
SoundNote["D5", {beatFour_, _}, "Trumpet", ___],
SoundNote["C5", {_, _}, "Trumpet", ___],
SoundNote["C5", {beatFive_, _}, "Trumpet", ___]
} :> With[
{
(* the offbeat nature of this phrase requires some manual work
to get things lined up in terms of actual beats *)
pickupBeatStart = pickupBeatAnd - (beatOne - pickupBeatAnd),
beatThree = beatThreeAnd - (beatFour - beatThreeAnd)
},
<|
"PhraseName" -> "Your boughs so green in summertime",
"PickupBeat" -> pickupBeatStart,
"TargetMeasureBeats" -> {beatOne, beatTwo, beatThree},
"BeatLength" ->
Mean@Differences[{pickupBeatStart, beatOne, beatTwo, beatThree,
beatFour, beatFive}]
|>
]
];
anchorData0 =
Join[anchorDataOChristmasTree, anchorDataYourBoughsSoGreen] //
SortBy[#PickupBeat &];
meanBeatLength = Mean[anchorData0[[All, "BeatLength"]]];
(* add enough beats to fill the end of the song, which ends on beat 2 *)
anchorData =
Append[anchorData0, <|
"TargetMeasureBeats" -> (lastBeat + {-1, 0, 1}*
Last[anchorData0]["BeatLength"]),
"BeatLength" -> Last[anchorData0]["BeatLength"]|>];
anchorData =
Append[anchorData, <|
"TargetMeasureBeats" -> (lastBeat + ({-1, 0, 1} + 3)*
Last[anchorData]["BeatLength"]),
"BeatLength" -> Last[anchorData]["BeatLength"]|>];Интерполируйте ритм между и во время фраз:
interpolateAnchor = Apply[
Function[{currentAnchor, nextAnchor},
With[
{targetMeasureLastBeat =
Last[currentAnchor["TargetMeasureBeats"]],
nextMeasureFirstBeat =
First[nextAnchor["TargetMeasureBeats"]]},
DeleteDuplicates@Join[
currentAnchor["TargetMeasureBeats"],
Range[targetMeasureLastBeat,
nextMeasureFirstBeat - currentAnchor["BeatLength"]/4.,
Mean[{currentAnchor["BeatLength"], nextAnchor["BeatLength"]}]]]
]]];
measureBeats = Flatten@BlockMap[interpolateAnchor, anchorData, 2, 1];
measureBeats // Length144
Ритм незначительно меняется, и, если не принимать во внимание вышеописанный метод привязки, это может привести к фазированию между движением и звуком:
Histogram[Differences[measureBeats], PlotTheme -> "Detailed", PlotRange -> Full]
(* add pickup beat at start *)
swayControlPoints =
Prepend[Join @@ (Partition[measureBeats, 3, 3, 1, {}] //
MapIndexed[
Function[{times, index}, {#, (-1)^(Mod[index[[1]], 2] + 1)} & /@
times]]), {firstBeat, -1}];
swayControlPointPlot =
ListPlot[swayControlPoints, Joined -> True, Mesh -> All,
AspectRatio -> 1/6, PlotStyle ->
{Darker[Purple]}, PlotTheme -> "Detailed",
MeshStyle -> PointSize[0.008], ImageSize -> 600,
Epilog -> {Darker[Green], Thick,
InfiniteLine[{{#, -1}, {#, 1}}] & /@ {firstBeat, secondBeat,
lastBeat}}];
sway = BSplineFunction[
Join[{{0, 0}},
Select[swayControlPoints, #[[1]] < tMax &], {{100, 0}}],
SplineDegree -> 3];
sh = Show[{swayControlPointPlot,
ParametricPlot[sway[t], {t, 0, tMax}, PlotPoints -> 2500]}]
{Show[sh, PlotRange -> {{0, 10}, All}], Show[sh, PlotRange -> {{90, 105}, All}]}
Теперь небольшое отступление: Интерполяция с B-сплайнами дает приятные гладкие кривые. В отличие от Interpolation, фактические данные не находятся на результирующей кривой. Это выглядит красиво и гладко, и это то, что мы хотим для визуальных целей этой анимации. Но интерполяция — для пары точек. Это означает, что для данного аргумента (между 0 и 1) функции B-сплайна мы не получаем линейную интерполяцию по первому аргументу. В место этого, нужно инвертировать интерполяцию, чтобы получить время как функцию переменной параметра интерполяции. Принимая во внимание этот эффект, важно правильно согласовать музыку с движениями веток.
swayTimeCoordinate = Interpolation[Table[{t, sway[t/100][[1]]}, {t, 0, 100, 0.1}], InterpolationOrder -> 1]
Этот график показывает разницу между интерполяцией и измененным параметром функции B-сплайна.
Plot[swayTimeCoordinate[t] - t, {t, 0, 100}]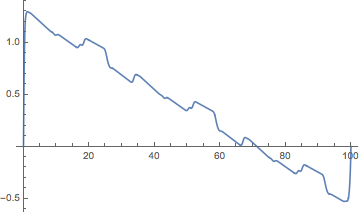
swayOfTime[t_] := sway[swayTimeCoordinate[t]/100][[2]]
Plot[swayOfTime[t], {t, 0, 10}]
Визуализируйте фразы и их отношение к движению с помощью всплывающей подсказки и цветных прямоугольников:
phraseGraphics = BlockMap[
Apply[
Function[{currentAnchor, nextAnchor},
With[
{phraseStart = currentAnchor["PickupBeat"],
phraseEnd =
nextAnchor["PickupBeat"] - currentAnchor["BeatLength"]},
{Switch[currentAnchor["PhraseName"],
"O Christmas Tree", Opacity[0.25, Gray],
"Your boughs so green in summertime",
Opacity[0.25, Darker@Green],
_, Black],
Tooltip[
Polygon[
{{phraseStart, -10}, {phraseStart, 10}, {phraseEnd,
10}, {phraseEnd, -10}}],
Grid[{{currentAnchor["PhraseName"], SpanFromLeft},
{"Phrase Start:", phraseStart}, {"Phrase End:", phraseEnd}
}]]}]]],
Append[anchorData0, <|"PickupBeat" -> lastBeat + meanBeatLength|>],
2, 1];
Show[swayControlPointPlot,
ParametricPlot[sway[t], {t, 0, Last[measureBeats]},
ImageSize -> Full, PlotPoints -> 800, AspectRatio -> 1/8,
PlotTheme -> "Detailed", PlotRangePadding -> Scaled[.02]],
Prolog -> phraseGraphics]
Движения дирижера
Дирижер выполняет простое периодическое движение, синхронизированное с музыкой.
threePatternPoints = {{0, -1}, {-1, -0}, {0, 1}};
threePatternBackground = ListPlot[
MapIndexed[
Callout[#1, StringTemplate["Beat #`` @ ``"][First@#2, #1], Left] &,
threePatternPoints],
PlotTheme -> "Minimal", Axes -> False, AspectRatio -> 1,
PlotStyle -> Directive[Black, PointSize[0.025]],
PlotRange -> {{-2, 0.75}, {-1.5, 1.5}}];
conductorControlTimes = swayControlPoints[[All, 1]];
(* basic conductor control points for interpolation *)
conductorControlPoints =
MapIndexed[{conductorControlTimes[[First[#2]]], #1} &,
Join @@ ConstantArray[RotateRight[threePatternPoints, 1],
Floor@(Length[conductorControlTimes]/3)]];
(* the shape is okay, but not perfect *)
conductor = Interpolation[conductorControlPoints];
(* adding pauses before/after the beat improves the shape of the
curves and makes the beats more obvious *)
conductorControlPointsWithPauses =
Join @@
({# - {meanBeatLength/8., -0.15*
Normalize[
Mean[threePatternPoints] - #[[
2]]]}, #, # + {meanBeatLength/8.,
0.15*Normalize[
Mean[threePatternPoints] - #[[
2]]]}} & /@
conductorControlPoints); На этот раз я использую Interpolation.
conductorWithPauses =
Interpolation[conductorControlPointsWithPauses,
InterpolationOrder -> 5];Вот результирующая форма дирижерской палочки.
Manipulate[
Show[threePatternBackground,
ParametricPlot[
conductorWithPauses[t], {t,
Max[firstBeat,(*tmax-2*meanBeatLength*)0], tmax},
PerformanceGoal -> "Quality"],
Epilog -> {Red, PointSize[Large], Point[conductorWithPauses[tmax]]},
ImageSize -> Large], {{tmax, lastBeat, "t"}, firstBeat + 0.0001,
lastBeat, Appearance -> "Labeled"},
SaveDefinitions -> True]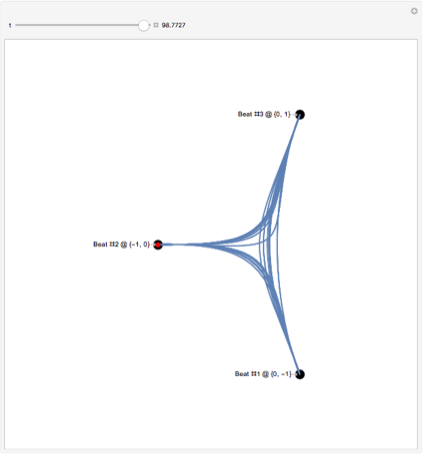
Движения веток по отношению к голосам
Существуют различные способы перевода звука в движения ветвей. Мы дадим два варианта: один связанный с частотой звуков, а другой — на основе нот.
Вариант 1
Первый перевод с голоса на 2D движения: вертикальное движение: сглаженная частота горизонтального движения голоса: различие текущей сглаженной частоты голоса до чуть более ранней частоты
?Delay = 0.3;
voice??[j_][time_] :=
If[0 < time < tMax,(* smoothing factor *)
Sin[Pi time/tMax]^0.25 {voiceFunction[j][1. time] -
voiceFunction[j][time - ?Delay],
voiceFunction[j][1. time]}, {0, 0}]
ParametricPlot[voice??[1][t], {t, 0, tMax},
AspectRatio -> 1, PlotRange -> All, Frame -> True, Axes -> False,
PlotStyle -> Thickness[0.002]]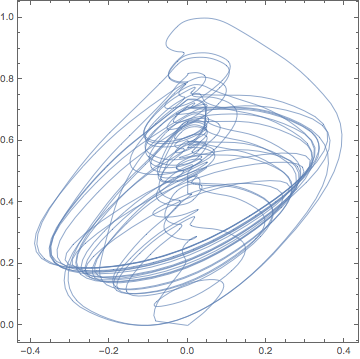
Вариант 2
Первый перевод с голоса на 2D движения: вертикальное движение: заметим изменение горизонтального движения: качание
value = -1;
interpolateDance[{{t1_, t2_}, {t3_, t4_}}, t_] :=
With[{y1 = value, y2 = value = -value},
{{y1, t1 < t < t2}, {((y1 - y2) t - (t3 y1 - t2 y2))/(t2 - t3),
t2 < t < t3}}];
dancingPositionPiecewise[notes : {__SoundNote}] :=
With[{noteTimes =
Cases[notes,
SoundNote[_, times : {startTime_, endTime_}, ___] :> times]},
value = -1;
Quiet[Piecewise[
DeleteDuplicatesBy[
Join @@ BlockMap[interpolateDance[#, t] &, noteTimes, 2, 1],
Last], 0]
]];
tEnd = Max[voices[[All, All, 2]]];
dancingPositions = dancingPositionPiecewise /@ voices;
Plot[Evaluate[KeyValueMap[Legended[#2, #1] &, dancingPositions]], {t,
0, 50},
PlotRangePadding -> Scaled[.05], PlotRange -> {All, {-1, 1}},
ImageSize -> Large, PlotTheme -> "Detailed", PlotLegends -> None]
dancingPositionPiecewiseList = Normal[dancingPositions][[All, 2]];
bsp = BSplineFunction[
Table[Evaluate[{t, dancingPositionPiecewiseList[[2]]}], {t, 0, 100,
0.2}]]
ParametricPlot[bsp[t], {t, 0, 1}, AspectRatio -> 1/4,
PlotPoints -> 2000]
Do[voiceIF[j] =
BSplineFunction[
Table[Evaluate[{t, dancingPositionPiecewiseList[[j]]}], {t, 0, 100,
0.2}]],
{j, 4}]
Do[With[{j = j},
voiceTimeCoordinate[j] =
Interpolation[Table[{t, voiceIF[j][t/100][[1]]}, {t, 0, 100, 0.1}],
InterpolationOrder -> 1]],
{j, 4}]Окончательные движения концов веток с квадратом ?-? [-1,1] * [- 1,1].
Clear[voice??];
voice??[j_][time_] :=
If[0 < time < tMax,(* smoothing factor *) Sin[Pi time/tMax]^0.25*
{sway[swayTimeCoordinate[time]/tMax][[2]],
voiceIF[j][voiceTimeCoordinate[j][time]/tMax][[2]]}, {0, 0}]
Table[ListPlot[Table[ voice??[j][t], {t, 0, 105, 0.01}],
Joined -> True, AspectRatio -> 1,
PlotStyle -> Thickness[0.002]], {j, 4}]
Моделирование движений украшений
Теперь настало время (наконец) немного поработать с физикой. Украшения (шарик, пятиконечная звезда) я буду моделировать как вынужденный сферический маятник с трением. Форсирование реализуется через положение кончиков веток, которое, в свою очередь, происходит от voice?? [j] [time].
Вынужденный сферический маятник
Сформируем Лагранжиан вынужденного сферического маятника в сферических координатах.
Clear[r, ?, R, X, Y, Z]
R[t_] := {X[t], Y[t], Z[t]}
r[t_] := R[t] +
L {Cos[?[t]] Sin[?[t]],
Sin[?[t]] Sin[?[t]], -Cos[?[t]]}
? = 1/2 r'[t].r'[t] - g r[t][[3]]-g (-L Cos[?[t]] + Z[t]) + 1/2 ((Derivative[1][Z][t] + L Sin[?[t]] Derivative[1][?][t])^2 + (Derivative[ 1][Y][t] + L Cos[?[t]] Sin[?[t]] Derivative[1][?][t] + L Cos[?[t]] Sin[?[t]] Derivative[1][?][ t])^2 + (Derivative[1][X][t] + L Cos[?[t]] Cos[?[t]] Derivative[1][?][t] — L Sin[?[t]] Sin[?[t]] Derivative[1][?][t])^2)
Добавим функцию диссипации Рэлея ? для учета трения.
? = 1/2 (\[ScriptF]? ?'[t]^2 + \[ScriptF]? ?'[t]^2);
eoms = {D[D[?, ?'[t]], t] -
D[?, ?[t]] == -D[?, ?'[t]],
D[D[?, ?'[t]], t] -
D[?, ?[t]] == -D[?, ?'[
t]]} // Simplify{([ScriptF]? + L^2 Sin[2 ?[t]] Derivative[1][?][t]) Derivative[ 1][?][t] + L Sin[?[t]] (-Sin?[t]t] + Cos[?[t][t] + L Sin?[t][t]) == 0, [ScriptF]? Derivative[1][?][t] + L (g Sin[?[t]] — L Cos[?[t]] Sin[?[t]] Derivative[1][?][t]^2 + Cos[?[t]] Cos?[t]t] + Cos[?[t]] Sin[?[t]t] + Sin[?[t][t] + L (?^??)[t]) == 0}
Пример, показывающий, что колебания быстро затухают с соответствующими значениями параметра [ScriptF] ?, [ScriptF] ?.
paramRules = { g -> 10,
L -> 1, \[ScriptF]? -> 1, \[ScriptF]? -> 1};
In[126]:= X[t_] := If[2 Pi < t < 4 Pi, 8 Cos[t], 8];
Y[t_] := If[2 Pi < t < 4 Pi, 4 Sin[t], 0];
Z[t_] := 0;
nds = NDSolve[{eoms /. paramRules, ?[0] == 1, ?'[0] ==
0, ?[0] == 0.001, ?'[0] == 0},
{?, ?}, {t, 0, 20}, PrecisionGoal -> 3, AccuracyGoal -> 3] 
Plot[Evaluate[{\[Phi][t], \[Theta][t]} /. nds[[1]]], {t, 0,
nds[[1, 2, 2, 1, 1, 2]]}, PlotRange -> All]
Graphics3D[
Table[With[{P = r[t] - R[t] /. nds[[1]] /. paramRules}, {Black,
Sphere[{0, 0, 0}, 0.02], Gray, Cylinder[{{0, 0, 0}, P}, 0.005],
Darker[Blue], Sphere[P, 0.02]}],
{t, 0, 20, 0.05}], PlotRange -> All]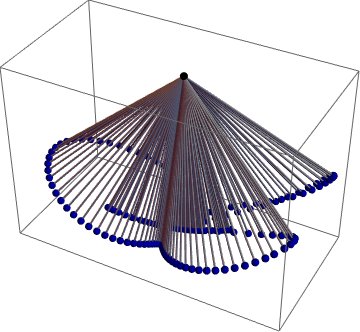
Рассчитать движения украшений
Получите направление ? и ? точек окончаний веток, интерполированных как функцию времени.
branchToVoice =
Association[
Flatten[Function[{v, bs}, (# -> v) & /@ bs] @@@
Normal[voiceBranches]]]<|2 -> 1, 9 -> 1, 14 -> 1, 17 -> 1, 19 -> 1, 24 -> 1, 27 -> 1, 3 -> 2, 13 -> 2, 15 -> 2, 16 -> 2, 21 -> 2, 26 -> 2, 1 -> 3, 4 -> 3, 5 -> 3,
12 -> 3, 18 -> 3, 20 -> 3, 6 -> 4, 8 -> 4, 10 -> 4, 11 -> 4, 22 -> 4, 23 -> 4, 25 -> 4|>
tValues = Table[1. t , {t, -5, 110, 0.1}];
Do[??Values =
Table[voice??[j][t] , {t, -5, 110, 0.1}];
if?[j] =
Interpolation[
Transpose[{tValues, ??Values[[All, 1]]}]];
if?[j] =
Interpolation[
Transpose[{tValues, ??Values[[All, 2]]}]],
{j, 4}]Вычислите движение украшений, смоделированных как сферический маятник. Чтобы получить некоторые изменения в передвижениях, я использую небольшие случайные отклонения от вертикали в качестве начальных условий для украшений (моделирование некоторых случайных движений теплового воздуха).
Для временного диапазона во второй половине я использую другую амплитуду (соответствующую более громкой музыке) для амплитуд усиления.
changeTimeList = {17.6, 42.2, 66.8, 83.1};
loudness[t_] :=
With[{?1 = 0.2, ?2 = 0.8, ?t = 1.5},
Which[t <= changeTimeList[[3]] - ?t, ?1,
changeTimeList[[3]] - ?t <= t <=
changeTimeList[[3]] + ?t,
?1 + (?2 -
1 ?1) (1 -
Cos[Pi (t - (changeTimeList[[
3]] - ?t))/(2 ?t)])/2,
changeTimeList[[3]] + ?t <= t <=
changeTimeList[[4]] - ?t , ?2,
changeTimeList[[4]] - ?t <= t <=
changeTimeList[[4]] + ?t,
?1 + (?2 -
1 ?1) (1 +
Cos[Pi (t - (changeTimeList[[
4]] - ?t))/(2 ?t)])/2,
t >= changeTimeList[[3]] + 1.5, ?1]
]
Plot[loudness[t], {t, 1, 100}, AxesOrigin -> {0, 0}, PlotRange -> All]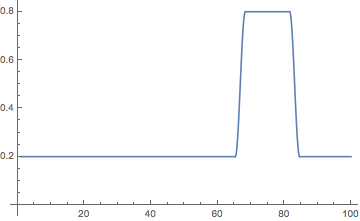
Off[General::stop];
SeedRandom[111];
Monitor[
Do[
branchEnd[j, {?_, ?_}] =
branchOnStemEndPoint[ allBranches[[j]], {?, ?}];
If[j =!= conductorBranch,
With[{v = branchToVoice[j]},
tipPosition[t_] =
branchEnd[j, loudness[t] {if?[v][t], if?[v][t]}]];
{X[t_], Y[t_], Z[t_] } = tipPosition[t];
paramRules = { g -> 20,
L -> 1, \[ScriptF]? -> 1, \[ScriptF]? -> 1};
While[ Check[
pendulum??[j][t_] =
NDSolveValue[{eoms /. paramRules,
?[0] == RandomReal[{-Pi, Pi}], ?'[0] ==
0.01 RandomReal[{-1, 1}],
?[0] == 0.01 RandomReal[{-1, 1}], ?'[0] ==
0.01 RandomReal[{-1, 1}]},
{?[t], ?[t]}, {t, 0, 105}, PrecisionGoal -> 4,
AccuracyGoal -> 4,
MaxStepSize -> 0.01, MaxSteps -> 100000, Method -> "BDF"];
False, True]] // Quiet],
{j, Length[allBranches]}], j]Вот сферические координатные углы для случайно выбранного украшения. Мы видим увеличение амплитуды колебаний при включении громкой музыки.
Plot[pendulum\[Phi]\[Theta][51][t][[2]], {t, 0, 105},
AspectRatio -> 1/4, PlotRange -> All]
Танцующая рождественская елка
Добавим несколько цветов для пятиконечных звездочек.
SeedRandom[11];
Do[randomColor[j] = RandomColor[];
randomAngle[j] = RandomReal[{-Pi/2, Pi/2}],
{j, Length[allBranches]}]Быстрое вертикальное начало и медленное окончание движений дирижера.
conductor??[t_] :=
Piecewise[
{{{0, 0},
t <= firstBeat/
2}, {(t - firstBeat/2)/(firstBeat/2) conductorControlPointsWithPauses[[
1, 2]], firstBeat/2 < t <= firstBeat}, {conductorWithPauses[t],
firstBeat < t <=
lastBeat}, {(tMax - t)/(tMax -
lastBeat) conductorControlPointsWithPauses[[-1, 2]],
lastBeat < t < tMax},
{{0, 0}, t >= tMax}}]Начало движения дирижера.
ListPlot[{Table[{t, conductor??[t][[1]]}, {t, -1, 3, 0.01}],
Table[{t, conductor??[t][[2]]}, {t, -1, 3, 0.01}]},
PlotRange -> All, Joined -> True]
With[{animationType = 2},
scalefactors[1][t_] :=
Switch[animationType, 1, {0.8, 1} , 2, loudness[t]];
scalefactors[2][t_] :=
Switch[animationType, 1, {1, 1} , 2, loudness[t]];
scalefactors[3][t_] :=
Switch[animationType, 1, {1, 1} , 2, loudness[t]];
scalefactors[4][t_] :=
Switch[animationType, 1, {1, 1} , 2, loudness[t]]
]
christmasTreeWithSwingingOrnaments[t_,
conductorEnhancementFactor : fc_,
conductorCandleAngle : ?c_, topRotationAngle : ?_,
opts___] :=
Graphics3D[{{Darker[Brown], stem},
(* first voice *)
branchOnStemWithBall[allBranches[[#]],
scalefactors[1][t] voice??[1][t],
Darker[Yellow, -0.1],
If[t < 0, {0, 0}, pendulum??[#][t]]] & /@
voiceBranches[[1]],
(* second voice *)
branchOnStemWithBall[allBranches[[#]],
scalefactors[2] [t] voice??[2][t],
Blend[{Red, Pink}],
If[t < 0, {0, 0}, pendulum??[#][t]]] & /@
voiceBranches[[2]],
(* third voice *)
branchOnStemWithFiveStar[allBranches[[#]],
scalefactors[3][t] voice??[3][t], randomColor[#],
Pi/4, If[t < 0, {0, 0}, pendulum??[#][t]]] & /@
voiceBranches[[3]],
(* fourth voice *)
branchOnStemWithCandle[#,
scalefactors[4][t] voice??[4][t],
Directive[White, Glow[GrayLevel[0.3]], Specularity[Yellow, 20]],
0] & /@ allBranches[[voiceBranches[[4]]]],
(* conductor *)
branchOnStemWithCandle[
allBranches[[conductorBranch]] {1, 1, 1 + fc},
conductor??[t],
Directive[Red, Glow[GrayLevel[0.1]],
Specularity[Yellow, 20]], ?c],
Rotate[top, ?, {0, 0, 1}]
}, opts, ViewPoint -> {2.8, 1.79, 0.1},
PlotRange -> {{-8, 8}, {-8, 8}, {-2, 15}},
Background -> RGBColor[0.998, 1., 0.867] ]Используйте низкую точку зрения, поскольку деревья обычно выше людей.
Show[christmasTreeWithSwingingOrnaments[70, 0.5, 0.8, 2],
PlotRange -> All, Boxed -> False]
Пусть идет снег!
Немного снега является обязательным для классического (белого) Рождества. Итак, давайте построим несколько 3D-снежинок, а затем заставим их падать. Вместо того, чтобы решать PDE (http://psoup.math.wisc.edu/papers/h3l.pdf), мы будем использовать клеточные автоматы на гексагональных сетках для создания некоторых форм, похожих на снежинки, с гексагональной симметрией.
Снежинки (2D)
Давайте возьмем какой-то код из демонстрации Эд Пегга «Снежинки-подобные шаблоны». Я просто импортирую ноутбук и программно извлекаю соответствующие ячейки, которые определяют переменные hex и snowflake.
ReleaseHold /@ (MakeExpression[#[[1]], StandardForm] & /@
Take[Cases[
Import["http://demonstrations.wolfram.com/downloadauthornb.cgi?name=SnowflakeLikePatterns"], Cell[_, "Input", ___], ?], 2]);
makeSnowflake[rule_, steps_] :=
Polygon[hex[#] & /@ Select[Position[Reverse[CellularAutomaton[
{snowflakes[[
rule]], {2, {{0, 2, 2}, {2, 1, 2}, {2, 2, 0}}}, {1,
1}}, {{{1}},
0}, {{{steps}}, {-steps, steps}, {-steps, steps}}]],
0], -steps - 1 < -#[[1]] + #[[2]] < steps + 1 &]]
SeedRandom[33];
Table[Graphics[{Darker[Blue],
makeSnowflake[RandomInteger[{1, 3888}],
RandomInteger[{10, 60}]]}], {4}]
Поскольку некоторые снежинки не работают, я выбираю те, которые интересны. Меня интересуют только снежинки, которые достаточно сложны.
denseFlakeQ[mr_MeshRegion] :=
With[{c = RegionCentroid[mr], pts = MeshCoordinates[mr]},
( Divide @@ MinMax[EuclideanDistance[c, #] & /@ pts]) < 1/3]
randomSnowflakes[] :=
Module[{sf},
While[(sf = Module[{},
TimeConstrained[
hexagons =
makeSnowflake[RandomInteger[{1, 3888}],
RandomInteger[{10, 60}]];
(Select[ConnectedMeshComponents[DiscretizeRegion[hexagons]],
(Area[#] > 120 && Perimeter[#]/Area[#] < 2 &&
denseFlakeQ[#]) &] /.
_ConnectedMeshComponents :> {}) // Quiet, 20, {}]]) === {}]; sf]
randomSnowflakes[n_] :=
Take[NestWhile[Join[#, randomSnowflakes[]] &, {}, Length[#] < n &], n]
SeedRandom[22];
randomSnowflakes[4]
normalizeFlake[mr_MeshRegion] :=
Module[{coords, center, coords1, size, coords2},
coords = MeshCoordinates[mr];
center = Mean[coords];
coords1 = (# - center) & /@ coords;
size = Max[Norm /@ coords1];
coords2 = coords1/size;
GraphicsComplex[coords2, {EdgeForm[], MeshCells[mr, 2]}]]Вот пять снежинок для дальнейшего использования.

Снежинки (3D)
Я добавляю эффект 2D снежинкам, дающий плоским телам иллюзию трёхмерности путём добавления к ним дополнительных поверхностей, чтобы получить 3D снежинки.
make3DFlake[flake2D_] :=
Module[{grc, reg, boundary, h, bc, rb, polys, pts},
grc = flake2D[[1]];
reg = MeshRegion @@ (grc /. _EdgeForm :> Nothing);
boundary = (MeshPrimitives[#, 1] &@RegionBoundary[reg])[[All, 1]];
h = RandomReal[{0.05, 0.15}];
bc =
Join[#1, Reverse[#2]] & @@@
Transpose[{Map[Append[#, 0] &, boundary, {-2}],
Map[Append[#, h] &, boundary, {-2}]}];
rb = RegionBoundary[reg];
boundary = (MeshCells[#, 1] &@rb)[[All, 1]];
polys =
Polygon[Join[#1, Reverse[#2]] & @@@
Transpose[{boundary, boundary + Max[boundary]}]];
pts =
Join[Append[#, 0] & /@ MeshCoordinates[rb],
Append[#, h] & /@ MeshCoordinates[rb]];
{GraphicsComplex[Developer`ToPackedArray[pts], polys],
MapAt[Developer`ToPackedArray[Append[#, 0]] & /@ # &, flake2D[[1]],
1],
MapAt[Developer`ToPackedArray[Append[#, h]] & /@ # &, flake2D[[1]],
1]}
]
listOfSnowflakes3D = make3DFlake /@ listOfSnowflakes;
Graphics3D[{EdgeForm[], #}, Boxed -> False,
Method -> {"ShrinkWrap" -> True}, ImageSize -> 120,
Lighting -> {{"Ambient", Hue[.58, .5, 1]}, {"Directional",
GrayLevel[.3], ImageScaled[{1, 1, 0}]}}] & /@ listOfSnowflakes3D
Модель падающего листа
Простая двумерная модель падающих листов была сделана Танабе и Канеко в 1994 году. Поэтому, чтобы получить некоторую интуицию о возможных формах падения, мы реализуем модель как интерактивную демонстрацию.
Manipulate[
Module[{eqs, nds, tmax, g = 10, ?, sign, V, x, y, u,
v, ?, ?, kpar = kperp/f, ? = 10^?exp},
? = ArcTan[u[t], v[t]];
sign = Piecewise[{{1, (v[t] < 0 &&
0 <= ? + ?[t] <= Pi) || (v[t] >
0 && -Pi <= ? + ?[t] <= 0)}}, -1];
V = Sqrt[u[t]^2 + v[t]^2];
eqs =
{D[x[t], t] == u[t],
D[y[t], t] == v[t],
D[u[t],
t] == -(kperp Sin[?[t]]^2 + kpar Cos[?[t]]^2) u[
t] +
(kperp - kpar) Sin[?[
t]] Cos[?[t]] v[t] -
sign Pi ? V^2 Cos[? + ?[t]] Cos[?],
D[v[t],
t] == -(kperp Cos[?[t]]^2 + kpar Sin[?[t]]^2) v[
t] +
(kperp - kpar) Sin[?[
t]] Cos[?[t]] u[t] +
sign Pi ? V^2 Cos[? + ?[
t]] Sin[?] - g,
D[?[t],
t] == -kperp ?[
t] - (3 Pi ? V^2/l) Cos[? + ?[
t]] Sin[? + ?[t]],
D[?[t], t] == ?[t]} /. kpar -> kperp/f;
nds = NDSolve[
Join[eqs, {x[0] == 0, y[0] == 0, u[0] == 0,
v[0] == 0.01, ?[0] == 0, ?[0] == ?0}],
{x, y, u, v, ?, ?}, {t, 0,
T}, MaxSteps -> 2000] // Quiet;
tmax = nds[[1, 2, 2, 1, 1, 2]];
Graphics[{Thickness[0.002], Gray,
Table[Evaluate[
Line[{{x[t], y[t]} - l/2 {Cos[?[t]], Sin[?[t]]},
{x[t],
y[t]} + l/2 {Cos[?[t]], Sin[?[t]]}}] /.
nds[[1]]],
{t, 0, tmax, tmax/n}],
Blue,
Line[Table[
Evaluate[{x[t], y[t]} /. nds[[1]]], {t, 0, tmax, tmax/200}]]},
AspectRatio -> ar, Frame -> True,
PlotRange -> All]],
"system parameters",
{{kperp, 5.1, Subscript["k", "L"]}, 0.01, 10,
Appearance -> "Labeled"},
{{f, 145,
Row[{Subscript["k", "L"], "/",
Subscript["k", "?"]}]}, 0.01, 200,
Appearance -> "Labeled"},
{{?exp, -0.45, Log["?"]}, -3, 1, Appearance -> "Labeled"},
{{l, 0.63}, 0.01, 10, Appearance -> "Labeled"} ,
Delimiter,
"fall parameters",
{{?0, 1, Subscript["?", "0"]}, -Pi, Pi,
Appearance -> "Labeled"},
{{T, 2, "falling time"}, 0, 10, Appearance -> "Labeled"} ,
Delimiter,
"plot",
{{ar, 1, "aspect ratio"}, {1, Automatic}},
{{n, 200, "snapshots"}, 2, 500, 1}]
Я буду моделировать процесс падения феноменологически и эвристически, а не через решение дифференциальных уравнений. Со значениями плотности снежинок и воздуха вместе с их отношением толщина / площадь они падают в основном прямо вниз, с небольшими боковыми движениями и внутренними вращениями.
Падение снежинок
Моделируем внутренние вращения вокруг центра масс, а также некоторые небольшие боковые движения.
randomParametrizedRotationMatrix[n_, ?_] := Function @@ {?,
Module[{phi, s, c},
Do[phi[i] =
Sum[RandomReal[{-1, 1}] Sin[
RandomReal[{0, n}] ? + 2 Pi RandomReal[]], {n}];
{c[i], s[i]} = {Cos[phi[i]], Sin[phi[i]]}, {i, 3}];
{{c[1], s[1], 0}, {-s[1], c[1], 0}, {0, 0, 1}}.
{{c[2], 0, s[2]}, {0, 1, 0}, {-s[2], 0, c[2]}}.
{{1, 0, 0}, {0, c[3], s[3]}, {0, -s[3], c[3]}}]};
randomParametrizedPathFunction := Function[t,
Evaluate[{RandomReal[{-5, 5}] +
Sum[RandomReal[{-1, 1}]/# Cos[2 Pi # t] &[
RandomReal[{1, 4}]], {k, 5}],
RandomReal[{-5, 5}] +
Sum[RandomReal[{-1, 1}]/# Cos[2 Pi # t] &[
RandomReal[{1, 4}]], {k, 5}],
RandomReal[{2, 12}] - RandomReal[{1.5, 2.5}] t}]]
SeedRandom[55];
Do[rotMat[j] = randomParametrizedRotationMatrix[3, ?];
trans[j] = randomParametrizedPathFunction;
snowflakeColor[
j] = {{"Ambient",
Hue[RandomReal[{0.55, 0.6}], RandomReal[{0.48, 0.52}],
RandomReal[{0.95, 1}]]}, {"Directional",
GrayLevel[RandomReal[{0.28, 0.32}]],
ImageScaled[{1, 1, 0}]}}, {j, Length[listOfSnowflakes]}]
fallingSnowflake[flake_, {t_, ?_}] :=
flake /. GraphicsComplex[cs_, rest__] :>
GraphicsComplex[(?.# + t) & /@ cs, rest]
Manipulate[
Graphics3D[{EdgeForm[],
Table[{Lighting -> snowflakeColor[k],
fallingSnowflake[
listOfSnowflakes3D[[k]], {trans[k][t], rotMat[k][t]}]}, {k,
Length[listOfSnowflakes3D]}] },
PlotRange -> 6, ViewPoint -> {0, -10, 0}, ImageSize -> 400],
{{t, 3.2}, -5, 20}]
Для полной анимации использовалось несколько сотен снежинок.
Создание анимационных кадров
Теперь запустите анимацию, вытянув ветвь дирижера, а также поверните верхнюю часть во время воспроизведения музыки. Затем мы послушаем и рассмотрим один стих. После, мы двинемся один раз вокруг дерева и добавим немного снегопада. И затем приходит интересная часть, где дерево качает вокруг своими украшениями, потом успокаивается и убирает свою ветвь дирижера. Я генерирую 24 кадра для каждой секунды звука.
conductorBranchMaxfactor = 0.5;
conductorBranchLength[t_] :=
conductorBranchMaxfactor*
Which[t < -3, 0, -3 < t <= 0, (t + 3)/3., 0 <= t <= tMax, 1,
tMax < t < tMax + 3, (1 - (t - tMax)/3), True, 0];
topRotation[t_] :=
Which[t < -3 || t > tMax + 3, 0,
True, (1. - Cos[(t + 3)/(tMax + 6)]) 20 2 Pi];
viewPoint[t_] :=
With[{vp = {2.8, 1.79, 0.1}},
Which[t < changeTimeList[[1]] || t > changeTimeList[[2]], vp,
changeTimeList[[1]] <= t <= changeTimeList[[2]],
Module[{t0 = changeTimeList[[1]],
?t =
changeTimeList[[2]] - changeTimeList[[1]], ?vp},
?vp = -Pi (1 -
Cos[ Pi (t - t0)/?t]); {{Cos[?vp],
Sin[?vp], 0}, {-Sin[?vp], Cos[?vp],
0}, {0, 0, 1}}.vp +
{0, 0, 2 Sin[Pi (t - t0)/?t]^4 }]]]
ParametricPlot3D[
viewPoint[t], {t, changeTimeList[[1]], changeTimeList[[2]]},
BoxRatios -> {1, 1, 1}]
animationFrame[t_] :=
Show[christmasTreeWithSwingingOrnaments[t, conductorBranchLength[t],
1.4 conductorBranchLength[t], topRotation[t]],
Background -> None, Boxed -> False, SphericalRegion -> True,
ViewPoint -> viewPoint[t]]
Последний тест перед запуском экспорта кадров, который займет несколько часов:
animationFrame[35]
framesPerSecond = 24;
animationFrameDirectory =
"/Users/mtrott/Desktop/ConductingChristmasTreeAnimationFrames/";
Monitor[
Do[
With[{t = -3 + 1/framesPerSecond (frame - 1)}, gr = animationFrame[t];
Export[animationFrameDirectory <> IntegerString[frame, 10, 4] <> ".png", gr,
ImageSize -> 1800, Background -> None]
],
{frame, 1, framesPerSecond (100 + 2 3)}],
Row[{frame, " | ", Round[MemoryInUse[]/1024^2], "\[ThinSpace]MB" }]
]Теперь используйте свое любимое программное обеспечение для редактирования фильмов (например, Adobe After Effects) и поместите движущееся дерево, звук и снегопад вместе.
По вопросам приобретения лицензий обращайтесь info-russia@wolfram.com
Бесплатная триал версия Mathematica
Бесплатный триал Wolfram|One


Colorbit
Спасибо за перевод. В очередной раз поражаюсь огромными возможностями и гибкостью языка Wolfram. Хотелось бы узнать, возможно ли в Mathematica выполнить преобразование .waw в midi?
galinawri Автор
На сколько я понимаю, это довольно сложный процесс. Вопрос обсуждался на Stackoverflow: stackoverflow.com/questions/2126193/wav-to-midi-conversion