Здравствуйте!

С появлением библиотеки Python Control Systems Library [1], решение основных задач проектирования систем автоматического управления (САУ) средствами Python значительно упростилось и теперь практически идентично решению таких задач в математическом пакете Matlab.

Однако, проектирование систем управления с применение указанной библиотеки имеют ряд существенных особенностей, которых нет в документации [1], поэтому особенностям использования Python Control Systems Librar и посвящена данная публикация.

Начнём с инсталляции библиотеки. В документации говориться о загрузке двух модулей slycot и control, на самом деле для нормальной работы нужна ещё библиотека numpy+mkl, остальные устанавливаются автоматически при загрузке control.

Указанные модули можно скачать с сайта [2]. В документации так же сказано, что для интерфейса по умолчанию нужно просто импортировать контрольный пакет следующим образом: import control.

Однако, при таком импортировании библиотека не работает ни одном из примеров. Для импортирования библиотеки необходимо применить from control import* как и для импортировании окружения matlab: from control. matlab import *[1].

Рассматривать специализированную библиотеку Python Control Systems Library можно только применительно к задачам проектирования систем автоматического управления, поэтому мы так и поступим.

1. Модели соединений систем (функции tf и feedback)

Ввод передаточных функций:

# -*- coding: utf8 -*-
from control.matlab import *
f = tf(1, [1, 1]);
g = tf(1, [2 ,1]);

Параллельное соединение блоков или систем:

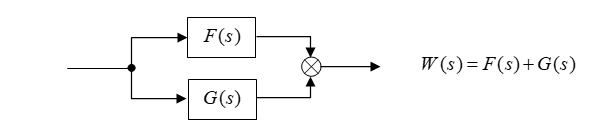
# -*- coding: utf8 -*-
from control.matlab import *
f = tf(1, [1, 1]);
g = tf(1, [2 ,1]);
w = f + g
print (w)

(3 s + 2)/(s^2 + 3 s + 1)

Последовательное соединение блоков или систем:

# -*- coding: utf8 -*-
from control.matlab import *
f = tf(1, [1, 1]);
g = tf(1, [2 ,1]);
w = f* g
print (w)

1/(2 s^2 + 3 s + 1)

Контур с обратной связью:



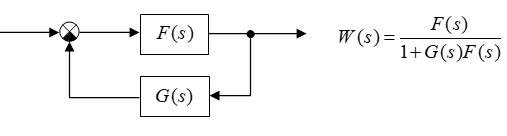
a) Контур с отрицательной обратной связью:

# -*- coding: utf8 -*-
from control.matlab import *
f = tf(1, [1, 1]);
g = tf(1, [2 ,1]);
w = feedback(f, g)
print(w)

(2 s + 1)/(2 s^2 + 3 s + 2)

б) Контур с положительной обратной связью:

# -*- coding: utf8 -*-
from control.matlab import *
f = tf(1, [1, 1]);
g = tf(1, [2 ,1]);
w = f/(1-f*g)
print(w)

(2 s^2 + 3 s + 1)/(2 s^3 + 5 s^2 + 3 s)

Вывод:

При помощи функций tf и feedback можно моделировать соединений блоков и систем.

2. Динамические и частотные характеристики систем автоматического управления (САУ)

Зададим передаточную функцию САУ:



Найдем ее динамические и частотные характеристики:

# -*- coding: utf8 -*-
from control.matlab import *
""" Создадим LTI-объект с именем w, для этого выполним:"""
num= [1., 2.]
den= [3., 4., 5.,3]
w= tf(num, den)
""" Найдем полюса и нули передаточной функции с использованием команд pole, zero"""
print('Передаточная функция САУ : \n %s'%w)
print("Полюса: \n %s"%pole(w))
print("Нули:\n %s -\n "%zero(w))

Передаточная функция САУ:

( s + 2)/(3 s^3 + 4 s^2 + 5 s + 3)

Полюса:

-0.26392546+1.08251346j
-0.26392546-1.08251346j
-0. 80548241+0.j
Нули: -2

Построим переходную функцию командой step(w):

# -*- coding: utf8 -*-
from control.matlab import *
import matplotlib.pyplot as plt
""" Создадим LTI-объект с именем w, для этого выполним:"""
num= [1., 2.]
den= [3., 4., 5.,3]
w= tf(num, den)
y,x=step(w)
plt.plot(x,y,"b")
plt.title('Step Responsse ') 
plt.ylabel('Amplitude')
plt.xlabel('Time(sec)')
plt.grid(True)
plt.show()

Построим импульсную переходную функцию командой impulse(w):

# -*- coding: utf8 -*-
from control.matlab import *
import matplotlib.pyplot as plt
""" Создадим LTI-объект с именем w, для этого выполним:"""
num= [1., 2.]
den= [3., 4., 5.,3]
w= tf(num, den)
y,x=impulse(w)
plt.plot(x,y,"r")
plt.title('impulse Responsse ') 
plt.ylabel('Amplitude')
plt.xlabel('Time(sec)')
plt.grid(True)
plt.show()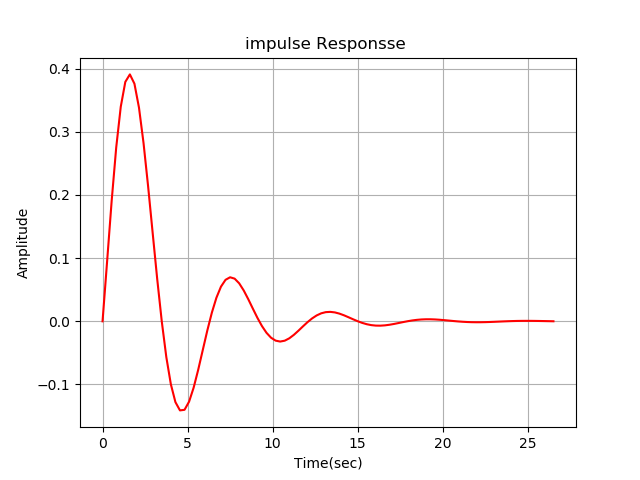

Диаграмму Боде получим используя команду bode(w):

# -*- coding: utf8 -*-
from control.matlab import *
import matplotlib.pyplot as plt
""" Создадим LTI-объект с именем w, для этого выполним:"""
num= [1., 2.]
den= [3., 4., 5.,3]
w= tf(num, den)
mag, phase, omega = bode(w, dB=True)
plt.plot()
plt.show()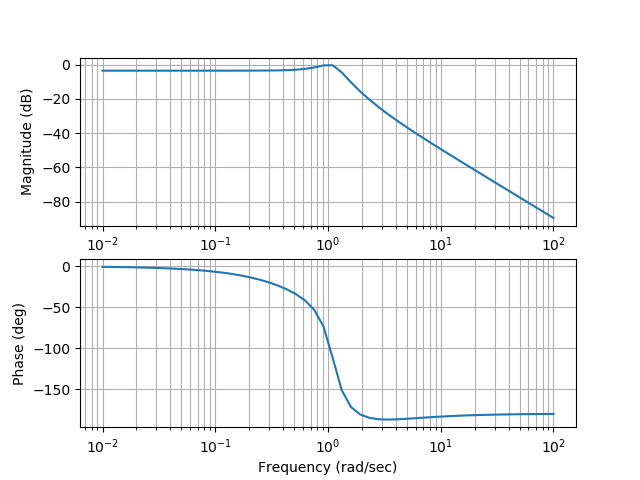

Вывод:

Построение bode диаграммы имеет некоторые особенности, приведенные в листинге.

Построим Найквист-диаграмму командой nyquist(w):

import matplotlib.pyplot as plt
from control.matlab import *
num= [1., 2.]
den= [3., 4., 5.,3]
w= tf(num, den)
plt.title('Nyquist Diagram ') 
plt.ylabel('Imaginary Axis')
plt.xlabel('Real Axis')
nyquist(w)
plt.grid(True)
plt.plot()
plt.show()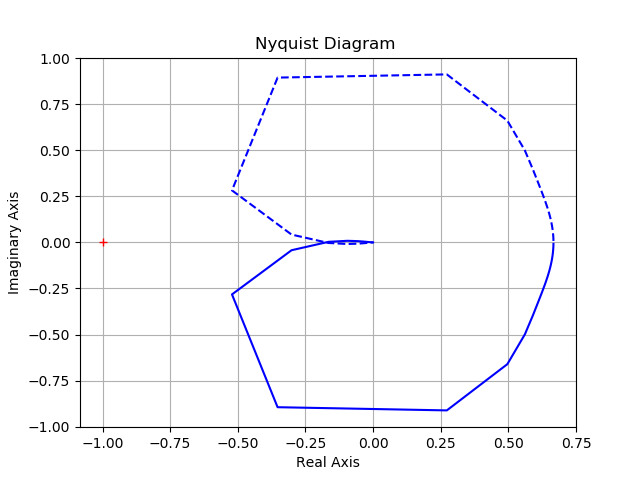

Вывод:

Построение Найквист- диаграммы имеет некоторые особенности, приведенные в листинге.

Мы рассмотрели простые задачи, теперь попробуем совсем немного поднапрячь библиотеку Python Control Systems Library.

3. Найдем дискретную передаточную функцию исполнительного механизма, уравнения состояния которого имеют вид:

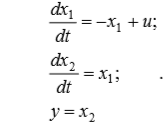(1)

Для вычисления воспользуемся матричной экспонентой:

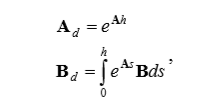(2)

где h – интервал квантования.

Найдем ее преобразование Лапласа от (2), которое будет равно.

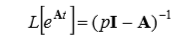(3)

где I – единичная матрица.

После подстановки в (3) матрицы А получим.

(4)

Вычислим обратную матрицу.

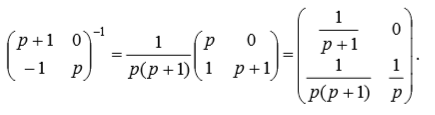(5)

Откуда, осуществляя z – преобразование последней матрицы, найдем матрицу перехода дискретной системы Ad.

(6)

где h – интервал дискретизации по времени.

Матрица Bd в соответствии с (2) будет равна.



Тогда дискретный аналог модели исполнительного механизма будет выглядеть:

(7)

Этот пример на Python Control Systems Library для h=0,1 запишется так:

# -*- coding: utf8 -*-
import matplotlib.pyplot as plt
from control.matlab import *
import numpy as np
A=np.matrix([[-1,0],[1,0]])
B=np.matrix([[1],[0]])
C=np.matrix([[0,1]])
D=0
sn=ss(A,B,C,D)
wd=tf(sn)
print("Непрерывная модель: \n %s"%sn)
print("Передаточная функция  \n %s"%wd)
y,x=step(wd)
plt.plot(x,y,"b")
plt.title('Step Responsse ') 
plt.ylabel('Amplitude')
plt.xlabel('Time(sec)')
plt.grid(True)
plt.show()
h=1
sd=c2d(sn,h)
print("Дискретная модель : \n %s"%sd)

Передаточная функция

1/(s^2+s)



Непрерывная модель:

 A = [[-1  0]
 [ 1  0]]
B = [[1]
 [0]]
C = [[0 1]]
D = [[0]]

Дискретная модель:

A = [[0.36787944 0. ]
 [0.63212056 1. ]]
B = [[0.63212056]
 [0.36787944]]
C = [[0 1]]
D = [[0]]
dt = 1

Вывод:

С использованием библиотеки на Python Control Systems Library получена математическая модель исполнительного механизма, основанная на системе дифференциальных уравнений (1). В модели использованы матричные операторы.

Уверен, что ценителям Python понравиться новая библиотека, существенно расширяющая возможности любимого языка программирования. Однако читатели знают, что любая новая библиотека требует большого труда для её адаптации к реальным задачам и только после этого она становиться востребованной и популярной.

Всем спасибо за внимание!

Ссылки:

1. Python Control Systems.

2. Unofficial Windows Binaries for Python Extension Packages.