Здравствуйте!

В предыдущей статье [1] мы рассмотрели некоторые особенности применения библиотеки Python Control Systems Library для проектирования систем управления. Однако, в последнее время широко используется проектирование систем управления с помощью переменных состояния, что значительно упрощает расчёты.

Поэтому, в данной статье на примере системы управления из публикации [2] мы рассмотрим упрощённую модель автопилота с использованием переменных состояния и функций tf, ss библиотеки Control.

Физические основы работы автопилота и системы уравнений полёта

Уравнения, управляющие движением летательного аппарата, представляют собой очень сложный набор из шести нелинейных связанных дифференциальных уравнений. Однако, при определенных предположениях, они могут быть разделены и линеаризованы в уравнения продольных и боковых перемещений. Полёт самолета определяется продольной динамикой.

Рассмотрим работу автопилота, который контролирует высоту воздушного судна. Основные координатные оси и силы, действующие на самолет, показаны на рисунке, приведенном ниже.



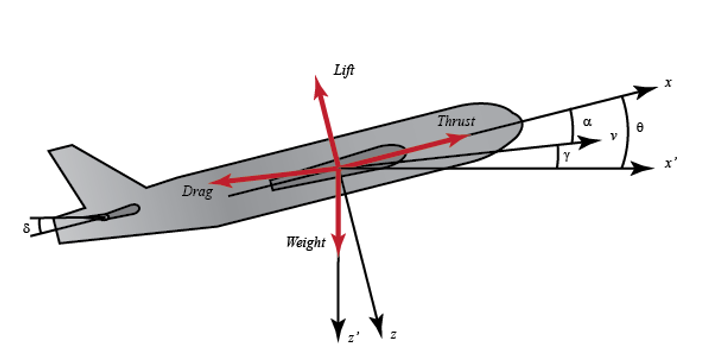
Будем считать, что самолет находится в устойчивом полёте с постоянной высотой и скоростью, таким образом, тяга, вес и подъемные силы уравновешивают друг друга в направлениях координатных осей.

Мы также предположим, что изменение угла тангажа ни при каких обстоятельствах не изменит скорость полета (это нереально, но немного упростит решение). В этих предположениях продольные уравнения движения для летательного аппарата могут быть записаны следующим образом:



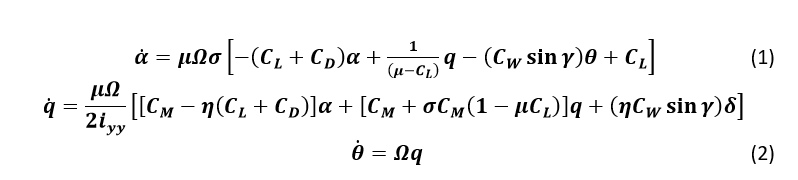
Обозначения переменных [3]:



Для этой системы вход будет углом отклонения 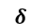, а выход будет углом тангажа

Введение численных значений в уравнения движения

Прежде чем найти передаточные функции из модели состояния пространства, подключим некоторые числовые значения, чтобы упростить приведенные выше уравнения моделирования:



Эти значения взяты из данных одного из коммерческих самолетов Boeing.

Передаточные функции

Чтобы найти передаточную функцию указанной системы, нам нужно взять преобразование Лапласа из приведенных выше уравнений моделирования. Напомним, что при нахождении передаточной функции должны приниматься нулевые начальные условия. Преобразование Лапласа приведенных уравнений показано ниже.



После нескольких шагов простых алгебраических преобразований, мы должны получить следующую передаточную функцию:

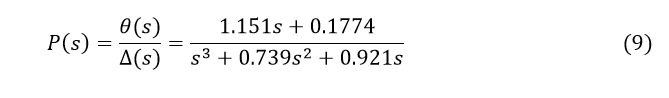
Пространство состояний объекта управления

Признавая тот факт, что приведенные выше уравнения моделирования уже находятся в форме переменных состояния, мы можем переписать их как матрицы, как показано ниже:



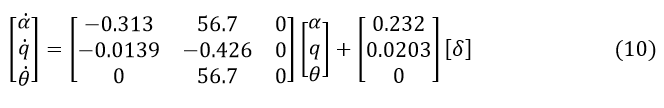
Для выходной характеристики модели — угла тангажа, можно записать следующее уравнение:

Исходные данные для моделирования

Следующим шагом будет выбор некоторых критериев проектирования. В этом примере мы разработаем контроллер обратной связи, так что в ответ на команду шага угла тангажа фактический угол наклона тангажа будет меньше 10%, время нарастания менее 2 секунд, время установления менее 10 секунд и установившаяся ошибка менее 2%.

Таким образом, требования к исходным данным следующие:

• Перегрузка менее 10%
• Время нарастания менее 2 секунд
• Время установления менее 10 секунд
• Стабильная ошибка менее 2%

Моделирование системы управления средствами Python

Теперь мы готовы представлять систему с использованием Python. Ниже приведен листинг модели системы управления в пространстве состояний.

from control import *
num= [1.151, 0.1774] # Числитель передаточной функции
den= [1, 0.739, 0.921,0] # Знаменатель передаточной функции
P_pitch= tf(num, den)
print("Генерация передаточной функции по соотношению (9):\n %s"%P_pitch)
A = [[-0.313, 56.7, 0],[ -0.0139, -0.426, 0], [0, 56.7, 0]];
B = [[0.232], [0.0203],[0]];
C = [[0, 0, 1]];
D =[[0]];
pitch_ss = ss(A,B,C,D)
print ("Модель пространства состояний \n системы   управления по уравнению (10): \n \n %s"%pitch_ss)

Результат роботы программы:

Генерация передаточной функции по соотношению (9):



Модель пространства состояний системы управления по уравнению (10):

A = [[-3.13e-01 5.67e+01 0.00e+00]
[-1.39e-02 -4.26e-01 0.00e+00]
[ 0.00e+00 5.67e+01 0.00e+00]]
B = [[0.232 ]
[0.0203]
[0. ]]
C = [[0 0 1]]
D = [[0]]

Вывод: Средства библиотеки Python Control Systems Library позволяют проводить исследование систем управления во временной области с помощью переменных состояния.

Ссылки:

1. Использование библиотеки Python Control Systems Library для проектирования систем автоматического управления.
2. Aircraft Pitch: System Modeling.
3. Extras: Aircraft Pitch System Variables.