Введение
Исследование системы управления во временной области с помощью переменных состояния широко используется в последнее время благодаря простоте проведения анализа.
Состоянию системы соответствует точка в определённом евклидовом пространстве, а поведение системы во времени характеризуется траекторией, описываемой этой точкой.
При этом математический аппарат включает готовые решения по аналоговому и дискретному LQR и DLQR контролерам, фильтра Калмана, и всё это с применением матриц и векторов, что и позволяет записывать уравнения системы управления в обобщённом виде, получая дополнительную информацию при их решении.
Целью данной публикации является рассмотрение решения задач проектирования систем оптимального управления методом описания пространства состояний с использованием программных средств Python.
Теория кратко
Векторно-матричная запись модели линейного динамического объекта с учетом уравнения измерения принимает вид:
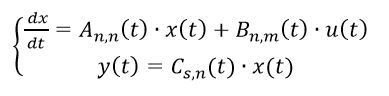(1)Если матрицы A(t), B(t) и C(t) не зависят от времени, то объект называется объектом с постоянными коэффициентами, или стационарным объектом. В противном случае объект будет нестационарным.
При наличии погрешностей при измерении, выходные (регулируемые) сигналы задаются линеаризованным матричным уравнением:
(2)где y(t) – вектор регулируемых (измеряемых) величин; C(t) – матрица связи вектора измерений с вектором состояний; v(t) – вектор ошибок измерений (помехи).
Структура линейной непрерывной системы, реализующая уравнения (1) и (2), приведена на рисунке:
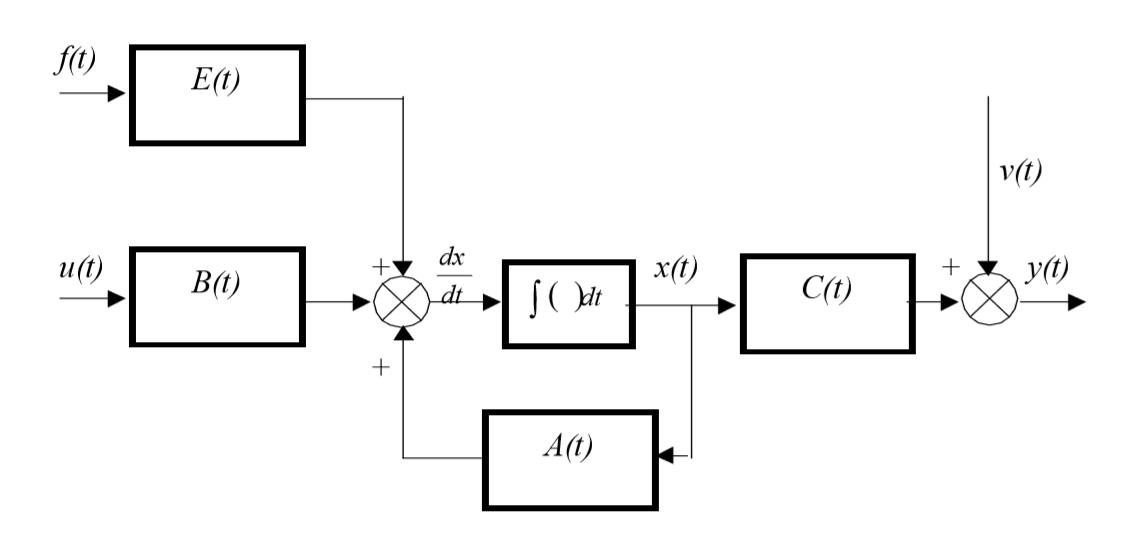
Данная структура соответствует математической модели объекта, построенной в пространстве состояний его входных x(t), u(t), выходных y(t) и внутренних, или фазовых координат x(t).
Для примера рассмотрим математическую модель двигателя постоянного тока с независимым возбуждением от постоянных магнитов. Система уравнений электрической и механической частей двигателя для рассматриваемого случая будет выглядеть так:
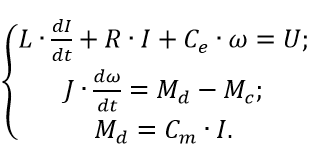(3)Первое уравнение отражает взаимосвязь между переменными в цепи якоря, второе — условия механического равновесия. В качестве обобщенных координат выберем ток якоря I и частоту вращения якоря ?.
Управлением являются напряжение на якоре U, возмущением — момент сопротивления нагрузки Mc. Параметрами модели являются активное сопротивление и индуктивность цепи и якоря, обозначенные соответственно Rя, и Lя, а также приведенный момент инерции J и конструктивные постоянные се и см (в системе СИ: Cе=См).
Разрешая исходную систему относительно первых производных, получим уравнения двигателя в пространстве состояний.
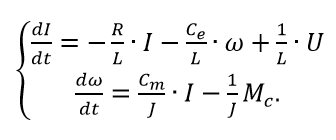(4)В матричном виде уравнения (4) примут вид (1):
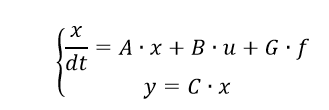(5)где вектор обобщенных координат
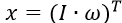, вектор управлений U =u (в рассматриваемом случае он является скаляром), вектор (скаляр) возмущений Mc=f. Матрицы модели:
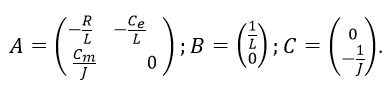(6)Если в качестве регулируемой величины выбрать частоту вращения, то уравнение измерения запишется в виде:
(7)а матрица измерений примет вид:
C=(0 1)
Сформируем модель двигателя в Python. Для этого вначале зададим конкретные значения параметров двигателя: U = 110 В; R =0,2 Ом; L = 0,006 Гн; J =0,1 кг/м2;Ce =Cm=1,3 В/С и найдем значения коэффициентом матриц объекта из (6).
Разработка программы формирующей модель двигателя с проверкой матриц на наблюдаемость и управляемость:
При разработке программы использовалась специальная функция def matrix_rank для определения ранга матрицы и функции, приведенные в таблице:
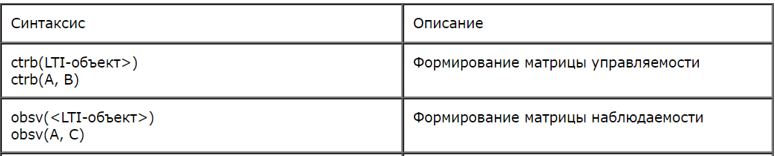
# -*- coding: utf8 -*-
from numpy import*
from control.matlab import *
from numpy.linalg import svd
from numpy import sum,where
import matplotlib.pyplot as plt
def matrix_rank(a, tol=1e-8):
s = svd(a, compute_uv=0)
return sum( where( s>tol, 1, 0) )
u=110 # Напряжение якоря
J=.1 # Момент инерции
c=1.3; # Конструктивный коэффициент
R=.2; L=.006 # Активное сопротивление и индуктивность якоря
A=matrix([[-R/L ,-c/L],[ c/J ,0]])
print ('Матрица А : \n %s'%A)
B=matrix([[1/L],[0]])
print ('Матрица B : \n %s '%B)
C=matrix([[0, 1]])
print ('Матрица C : \n %s '%C)
D=0
print ('Скаляр D : \n %s '%D)
sd=ss(A,B,C,D) #Задание модели объекта в пространстве состояний
wd=tf(sd) # Задание передаточной функции двигателя
print ('Передаточная функция двигателя : \n %s '%wd)
a=ctrb(A,B)
print(' Ранг матрицы управляемости : %s'%matrix_rank(a, tol=1e-8))
a=obsv(A,C)
print('Ранг матрицы наблюдаемости: %s'%matrix_rank(a, tol=1e-8))
y,x=step(wd) # Построение переходной характеристики
plt.plot(x,y,"b")
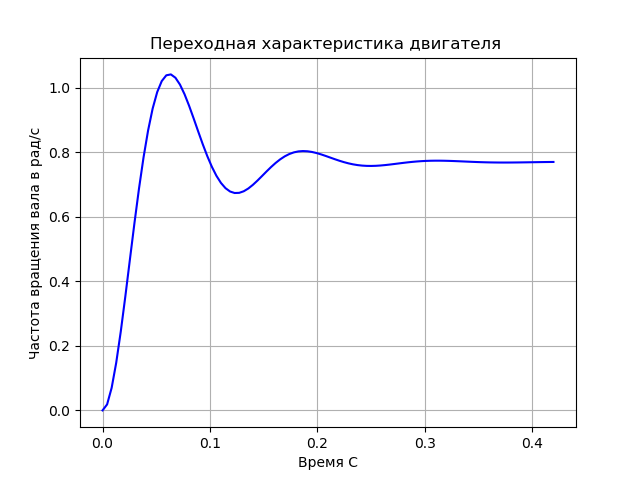
plt.title('Переходная характеристика двигателя ')
plt.ylabel('Частота вращения вала в рад/с')
plt.xlabel('Время С')
plt.grid(True)
plt.show()Результаты работы программы:
Матрица А:
[[ -33.33333333 -216.66666667]
[ 13. 0. ]]
Матрица B:
[[166.66666667]
[ 0. ]]
Матрица C:
[[0 1]]
Скаляр D:
0
Передаточная функция двигателя:
2167/(s^2 + 33.33 s + 2817)
Ранг матрицы управляемости: 2
Ранг матрицы наблюдаемости: 2
Выводы:
1. На примере двигателя постоянного тока с независимым магнитным возбуждением рассмотрена методика проектирования управления в пространстве состояний;
2. В результате работы программы получены передаточная функция, переходная характеристика, а так же ранги матриц управляемости и наблюдаемости. Ранги совпадают с размерностями пространства состояний, что подтверждает управляемость и наблюдаемость модели.
Пример проектирования оптимальной системы управления с дискретным dlqr контролером и полной обратной связью
Определения и терминология
Линейно-квадратичный регулятор (англ. Linear quadratic regulator, LQR) — в теории управления один из видов оптимальных регуляторов, использующий квадратичный функционал качества.
Задача, в которой система описывается линейными дифференциальными уравнениями, а показатель качества, представляет собой квадратичный функционал, называется задачей линейно-квадратичного управления.
Широкое распространение получили линейно-квадратичные регуляторы (LQR) и линейно-квадратичные гауссовы регуляторы (LQG).
Приступая к практическому решению задачи всегда нужно помнить об ограничениях
Для синтеза оптимального дискретного регулятора линейных стационарных систем нужна функция численного решения уравнения Беллмана.Такой функции в библиотеке Python Control Systems [1] нет, но можно воспользоваться функцией для решения уравнения Риккати, приведенной в публикации [2]:
def dlqr(A,B,Q,R):
"""Solve the discrete time lqr controller.
x[k+1] = A x[k] + B u[k]
cost = sum x[k].T*Q*x[k] + u[k].T*R*u[k]
"""
#ref Bertsekas, p.151
#first, try to solve the ricatti equation
X = np.matrix(scipy.linalg.solve_discrete_are(A, B, Q, R))
#compute the LQR gain
K = np.matrix(scipy.linalg.inv(B.T*X*B+R)*(B.T*X*A))
eigVals, eigVecs = scipy.linalg.eig(A-B*K)
return K, X, eigVals
Но нужно ещё учесть ограничения на синтез оптимального регулятора, приведенные в [3]:
- система, определяемая матрицами (A, B) должна быть стабилизируема;
- должны выполняться неравенства S> 0, Q – N/R–N.T>0, пара матриц (Q – N/R–N.T,
A – B/R–B.T) не должна иметь наблюдаемые моды с собственными значениями на
действительной оси.
После копаний в обширной и не однозначной теории, которую, по понятным причинам, я не привожу, задачу удалось решить, и все ответы можно прочитать прямо в комментариях к коду.
Структурная схема регулятора системы управления с обратной связью по всем переменным состояния изображена на рисунке:
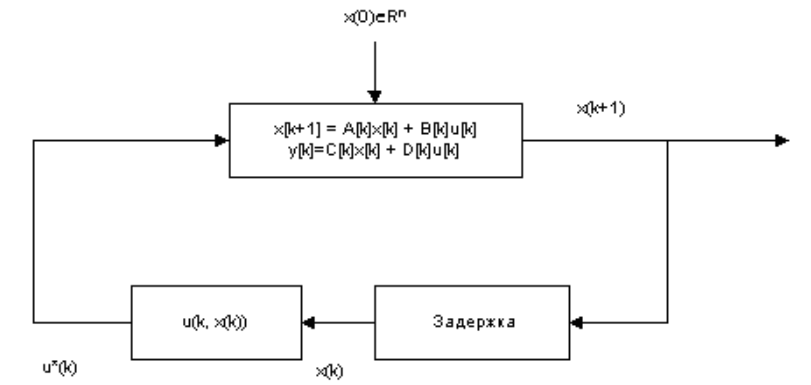
Для каждого начального состояния x0 оптимальный линейный регулятор порождает оптимальное программное управление u*(x, k) и оптимальную траекторию х*(k).
Программа, формирующая модель оптимального управления с dlqr контролером
from numpy import *
import scipy.linalg
import matplotlib.pyplot as plt
def dlqr(A,B,Q,R):
#Дискретное решение матричного уравнения Риккати x[k+1] = A x[k] + B u[k]
P= matrix(scipy.linalg.solve_discrete_are(A, B, Q, R))
#Дискретный контроллер DLQR
K = matrix(scipy.linalg.inv(B.T*P*B+R)*(B.T*P*A))
E, E1 = scipy.linalg.eig(A-B*K)
return K, P, E
"""Параметры системы"""
A=matrix([[1, 0],[ -2 ,1]])
B=matrix([[1, 0],[1, 0]]).T
"""Параметры качества управления"""
Q=matrix([[0.5, 0],[0, 0.5]])
R=matrix([[0.5,0],[0, 0.5]])
T =100# Время регулирования
SS=0.5# Величина шаг
N =int(T/SS)# Количество шагов
K, P, E=dlqr(A,B,Q,R)#Вычисление параметров контроллера
print("K= \n%s"%K)
print("P= \n%s"%P)
print("E= \n%s"%E)
x = zeros([2, N])
u= zeros([2, N-1])
x [0,0]=2
x [1,0]=1
for i in arange(0,N-2):
u[:, i]= dot(- K,x[:, i])
x[:, i+1]=dot(A,x[:, i])+dot(B,u[:, i])
x1= x[0,:]
x2= x[1,:]
t = arange(0,T,SS)
t1=arange(0.5,T,SS)
plt.subplot(221)
plt.plot(t, x1, 'b')
plt.grid(True)
plt.subplot(222)
plt.plot(t, x2, 'g')
plt.grid(True)
plt.subplot(223)
plt.plot(t1, u[0,:], 'y')
plt.grid(True)
plt.subplot(224)
plt.plot(t1, u[1,:], 'r')
plt.grid(True)
plt.show()
Результаты расчета:
K=
[[ 0.82287566 -0.17712434]
[ 0.82287566 -0.17712434]]
P=
[[ 3.73431348 -1.41143783]
[-1.41143783 1.16143783]]
E=
[0.17712434+0.17712434j 0.17712434-0.17712434j]
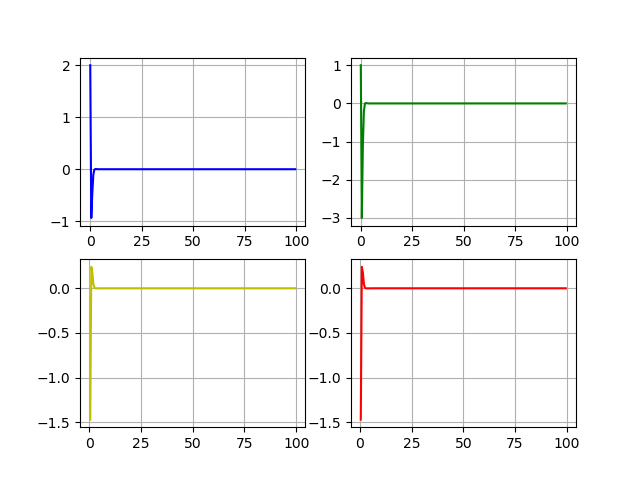
Динамика состояний и управлений: x1, x2, u1, u2.
Вывод
Отдельные задачи оптимального управления по типу приведенных можно решать средствами Python, комбинируя возможности библиотек Python Control Systems, SciPy,NumPy, что, безусловно, способствует популяризации Python, учитывая, что ранее такие задачи можно было решать только в платных математических пакетах.