Попробуйте решить задачу из онлайн-хакатона Geohack.112. Дано: территория Москвы и Московской области была разделена на квадраты размеров от 500 на 500 метров. В качестве исходных данных представлено среднее количество вызовов экстренных служб в день (номера 112, 101, 102, 103, 104, 010, 020, 030, 040). Рассматриваемый регион был поделен на западную и восточную часть. Участникам предлагается, обучившись по западной части, предсказать количество вызовов экстренных служб для всех квадратов восточной.
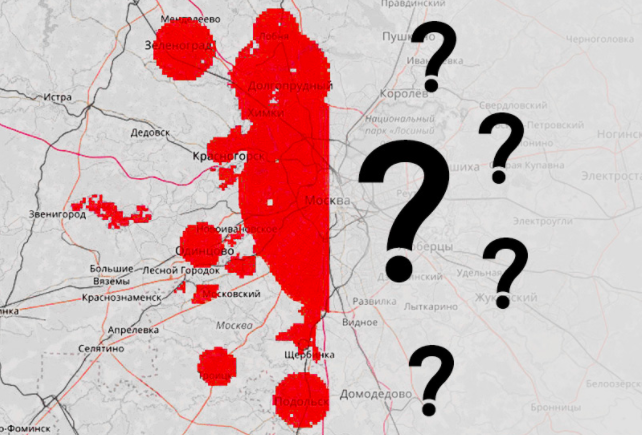
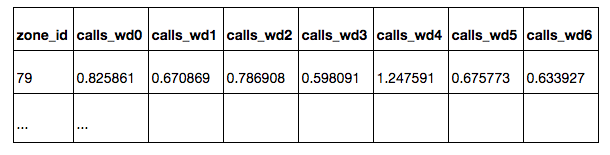
В таблице zones.csv перечислены все квадраты с указанием их координат. Все квадраты расположены в Москве, либо на небольшом расстоянии от Москвы. Квадраты, расположенные в западной части выборки, предназначены для обучения модели — для этих квадратов известно среднее число вызовов экстренных служб из квадрата в день:
calls_daily: по всем дням
calls_workday: по рабочим дням
calls_weekend: по выходным дням
calls_wd{D}: по дню недели D (0 — понедельник, 6 — воскресенье)
На квадратах из восточной части выборки необходимо построить прогноз числа вызовов по всем дням недели. Оценка качества предсказания будет производиться по подмножеству квадратов, в которое не входят квадраты, откуда вызовы поступают крайне редко. Подмножество целевых квадратов имеет is_target=1 в таблице. Для тестовых квадратов значения calls_* и is_target скрыты.
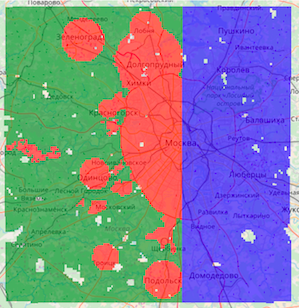
На карте обозначены квадраты трех типов:
Зеленые — из обучающей части, не целевые
Красные — из обучающей части, целевые
Синие — тестовые, на них необходимо построить прогноз
В качестве решения необходимо предоставить CSV таблицу с предсказаниями для всех тестовых квадратов, для каждого квадрата — по всем дням недели.
Качество оценивается только по подмножеству целевых квадратов. Участникам неизвестно, какие из квадратов целевые, однако принцип выбора целевых квадратов в обучающей и тестовой части — идентичен. Во время соревнования качество оценивается на 30% тестовых целевых квадратов (выбраны случайно), в конце соревнования итоги подводятся по оставшимся 70% квадратов.
Метрика качества предсказаний — коэффициент ранговой корреляции Kendall's Tau-b, считается как доля пар объектов с неправильно упорядоченными предсказаниями с поправкой на пары с одинаковым значением целевой переменной. Метрика оценивает порядок, в котором предсказания соотносятся друг с другом, а не их точные значения. Разные дни недели считаются независимыми элементами выборки, т.е. коэффициент корреляции считается по предсказаниям для всех тестовых пар (zone_id, день недели).
Предсказание числа вызовов можно осуществить методами машинного обучения. Для этого каждому квадрату необходимо построить вектор с признаковым описанием. Обучив модель на размеченной западной части Москвы, ее можно будет использовать для предсказания целевой переменной в восточной части.
По условиям соревнования, данные для решения задачи можно брать из любых открытых источников. Когда речь идет об описании небольшой области на карте, первое что приходит в голову — OpenStreetMap, открытая некоммерческая электронная карта, которая создается руками сообщества.
Карта OSM представляет собой набор элементов трех видов:
Node: точки на карте
Way: дороги, площади, задаются набором точек
Relation: связи между элементами, например объединение дороги из нескольких частей
Элементы могут иметь набор тегов — пар ключ-значение. Вот пример магазина, который указан на карте как элемент типа Node:
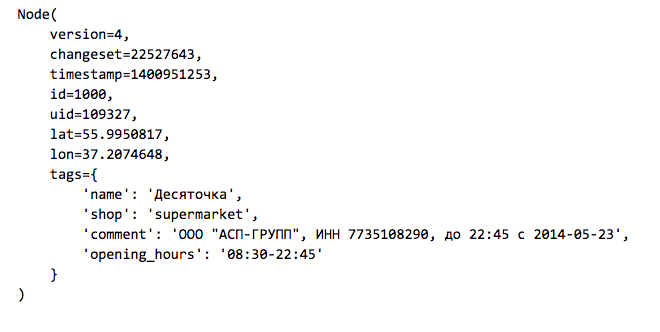
Актуальную выгрузку данных OpenStreetMap можно взять с сайта GIS-Lab.info. Так как нас интересует Москва и ее ближайшее окружение, загрузим файл RU-MOS.osm.pbf — часть OpenStreetMap из соответствующего региона в бинарном формате osm.pbf. Для чтения таких файлов из Python имеется простая библиотека osmread.
Прежде чем начать работать, считаем из OSM все элементы типа Node из нужной нам области, которые имеют теги (остальные отсеим и не будем использовать в дальнейшем).
Организаторы соревнования подготовили бейзлайн, который доступен по ссылке. Весь код, который приведен далее содержится в этом бейзлайне.
Работая в Python, геоданные можно быстро визуализировать на интерактивной карте при помощи библиотеки folium, у которой под капотом Leaflet.js — стандартное решение для отображения OpenStreetMap.
Агрегируем полученный набор точек по квадратам и построим простые признаки:
1. Расстояние от центра квадрата до Кремля
2. Число точек в радиусе R от центра квадрата (для различных значений R)
a. всех точек с тегами
b. ж/д станций
c. магазинов
d. остановок общественного транспорта
3. Максимальное и среднее расстояние от центра квадрата до ближайших точек перечисленных выше видов
Для быстрого поиска точек, находящихся в близости с центром квадрата, будем использовать структуру данных k-d tree, реализованную в пакете SciKit-Learn в классе NearestNeighbors.
В итоге для каждого квадрата из обучающей и тестовой выборки имеем признаковое описание, которое можно использовать для предсказания. Небольшой модификацией предложенного кода можно учесть в признаках объекты других типов. Участники могут добавлять свои признаки, тем самым давая модели больше информации о городской застройке.
Предсказание числа вызовов
Опытные участники соревнований по анализу данных знают, что для получения высокого места важно не только смотреть на публичный лидерборд, но и делать собственную валидацию на тренировочной выборке. Сделаем простое разбиение тренировочной части выборки на подвыборки для обучения и валидации в соотношении 70/30.
Возьмем только целевые квадраты и обучим модель случайного леса (RandomForestRegressor) предсказывать среднее число вызовов в день.
Оценим качество на валидационной подвыборке, для всех дней недели построим одинаковый прогноз. Метрика качества — непараметрический коэффициент корреляции Кендалла tau-b, он реализован в пакете SciPy в виде функции scipy.stats.kendalltau.
Получается Validation score: 0.656881482683
Это неплохо, т.к. значение метрики 0 означает отсутствие корреляции, а 1 — полное монотонное соответствие реальных значений и предсказанных.
До вхождения в ряды участников, которые получат приглашение на Data Fest, остается один небольшой шаг: построить таблицу с предсказаниями на всех тестовых квадратах и отправить их в систему.
Зачем анализировать геоданные?
Основными источниками данных, не только пространственных (географических), но и временных, для любой телеком-компании являются расположенные на всей территории стран обслуживания комплексы аппаратуры для приема и передачи сигнала — Базовые Станции (БС). Пространственный анализ данных труднее технически, но может принести существенную пользу и получить признаки, добавляющие весомый вклад в эффективность моделей машинного обучения.
В компании МТС использование географических данных помогает расширить базу знаний. Они могут использоваться для повышения качества предоставляемого сервиса при анализе жалоб абонентов на качество связи, улучшения зоны покрытия сигнала связи, планирования развития сети и решения других задач, где пространственно временная связь является важным фактором.
Возрастающая, особенно в крупных городах, плотность населения, стремительное развитие объектов инфраструктуры и дорожной сети, космические снимки и векторные карты, количество строений и POI (points of interest) с открытых карт местности, связанных с оказание сервисных услуг – все эти пространственные данные можно получить из внешних источников. Такие данные могут применяться как дополнительный источник информации, а также позволят получить объективную картину вне зависимости от покрытия сети.
Понравилась задача? Тогда мы приглашаем вас принять участие в онлайн-хакатоне по анализу географических данных Geohack.112. Регистрируйтесь и загружайте свои решения на сайт до 24 апреля. Авторы трех лучших результатов получат денежные призы. Отдельные номинации предусмотрены для участников, представивших лучшее публичное решение задачи и лучшую визуализацию журналистики данных. Общий призовой фонд МТС GeoHack — 500 000 рублей. Мы надеемся увидеть новые интересные подходы к генерации пространственных фичей, визуализации геоданных и использования новых открытых источников информации.
Награждение победителей пройдет 28 апреля на конференции DataFest.

В таблице zones.csv перечислены все квадраты с указанием их координат. Все квадраты расположены в Москве, либо на небольшом расстоянии от Москвы. Квадраты, расположенные в западной части выборки, предназначены для обучения модели — для этих квадратов известно среднее число вызовов экстренных служб из квадрата в день:
calls_daily: по всем дням
calls_workday: по рабочим дням
calls_weekend: по выходным дням
calls_wd{D}: по дню недели D (0 — понедельник, 6 — воскресенье)
На квадратах из восточной части выборки необходимо построить прогноз числа вызовов по всем дням недели. Оценка качества предсказания будет производиться по подмножеству квадратов, в которое не входят квадраты, откуда вызовы поступают крайне редко. Подмножество целевых квадратов имеет is_target=1 в таблице. Для тестовых квадратов значения calls_* и is_target скрыты.
На карте обозначены квадраты трех типов:
Зеленые — из обучающей части, не целевые
Красные — из обучающей части, целевые
Синие — тестовые, на них необходимо построить прогноз

В качестве решения необходимо предоставить CSV таблицу с предсказаниями для всех тестовых квадратов, для каждого квадрата — по всем дням недели.

Качество оценивается только по подмножеству целевых квадратов. Участникам неизвестно, какие из квадратов целевые, однако принцип выбора целевых квадратов в обучающей и тестовой части — идентичен. Во время соревнования качество оценивается на 30% тестовых целевых квадратов (выбраны случайно), в конце соревнования итоги подводятся по оставшимся 70% квадратов.
Метрика качества предсказаний — коэффициент ранговой корреляции Kendall's Tau-b, считается как доля пар объектов с неправильно упорядоченными предсказаниями с поправкой на пары с одинаковым значением целевой переменной. Метрика оценивает порядок, в котором предсказания соотносятся друг с другом, а не их точные значения. Разные дни недели считаются независимыми элементами выборки, т.е. коэффициент корреляции считается по предсказаниям для всех тестовых пар (zone_id, день недели).
Читаем таблицу квадратов при помощи Pandas
import pandas
df_zones = pandas.read_csv('data/zones.csv', index_col='zone_id')
df_zones.head()Извлечение признаков из OpenStreetMap
Предсказание числа вызовов можно осуществить методами машинного обучения. Для этого каждому квадрату необходимо построить вектор с признаковым описанием. Обучив модель на размеченной западной части Москвы, ее можно будет использовать для предсказания целевой переменной в восточной части.
По условиям соревнования, данные для решения задачи можно брать из любых открытых источников. Когда речь идет об описании небольшой области на карте, первое что приходит в голову — OpenStreetMap, открытая некоммерческая электронная карта, которая создается руками сообщества.
Карта OSM представляет собой набор элементов трех видов:
Node: точки на карте
Way: дороги, площади, задаются набором точек
Relation: связи между элементами, например объединение дороги из нескольких частей
Элементы могут иметь набор тегов — пар ключ-значение. Вот пример магазина, который указан на карте как элемент типа Node:

Актуальную выгрузку данных OpenStreetMap можно взять с сайта GIS-Lab.info. Так как нас интересует Москва и ее ближайшее окружение, загрузим файл RU-MOS.osm.pbf — часть OpenStreetMap из соответствующего региона в бинарном формате osm.pbf. Для чтения таких файлов из Python имеется простая библиотека osmread.
Прежде чем начать работать, считаем из OSM все элементы типа Node из нужной нам области, которые имеют теги (остальные отсеим и не будем использовать в дальнейшем).
Организаторы соревнования подготовили бейзлайн, который доступен по ссылке. Весь код, который приведен далее содержится в этом бейзлайне.
Загрузка объектов из OpenStreetMap
import pickle
import osmread
from tqdm import tqdm_notebook
LAT_MIN, LAT_MAX = 55.309397, 56.13526
LON_MIN, LON_MAX = 36.770379, 38.19270
osm_file = osmread.parse_file('osm/RU-MOS.osm.pbf')
tagged_nodes = [
entry
for entry in tqdm_notebook(osm_file, total=18976998)
if isinstance(entry, osmread.Node)
if len(entry.tags) > 0
if (LAT_MIN < entry.lat < LAT_MAX) and (LON_MIN < entry.lon < LON_MAX)
]
# Сохраним список с выбранными объектами в отдельный файл
with open('osm/tagged_nodes.pickle', 'wb') as fout:
pickle.dump(tagged_nodes, fout, protocol=pickle.HIGHEST_PROTOCOL)
# Файл с сохраненными объектами можно будет быстро загрузить
with open('osm/tagged_nodes.pickle', 'rb') as fin:
tagged_nodes = pickle.load(fin)Работая в Python, геоданные можно быстро визуализировать на интерактивной карте при помощи библиотеки folium, у которой под капотом Leaflet.js — стандартное решение для отображения OpenStreetMap.
Пример визуализации при помощи folium
import folium
fmap = folium.Map([55.753722, 37.620657])
# нанесем ж/д станции
for node in tagged_nodes:
if node.tags.get('railway') == 'station':
folium.CircleMarker([node.lat, node.lon], radius=3).add_to(fmap)
# выделим квадраты с наибольшим числом вызовов
calls_thresh = df_zones.calls_daily.quantile(.99)
for _, row in df_zones.query('calls_daily > @calls_thresh').iterrows():
folium.features.RectangleMarker(
bounds=((row.lat_bl, row.lon_bl), (row.lat_tr, row.lon_tr)),
fill_color='red',
).add_to(fmap)
# карту можно сохранить и посмотреть в браузере
fmap.save('map_demo.html')Агрегируем полученный набор точек по квадратам и построим простые признаки:
1. Расстояние от центра квадрата до Кремля
2. Число точек в радиусе R от центра квадрата (для различных значений R)
a. всех точек с тегами
b. ж/д станций
c. магазинов
d. остановок общественного транспорта
3. Максимальное и среднее расстояние от центра квадрата до ближайших точек перечисленных выше видов
Для быстрого поиска точек, находящихся в близости с центром квадрата, будем использовать структуру данных k-d tree, реализованную в пакете SciKit-Learn в классе NearestNeighbors.
Построение таблицы с признаковым описанием квадратов
import collections
import math
import numpy as np
from sklearn.neighbors import NearestNeighbors
kremlin_lat, kremlin_lon = 55.753722, 37.620657
def dist_calc(lat1, lon1, lat2, lon2):
R = 6373.0
lat1 = math.radians(lat1)
lon1 = math.radians(lon1)
lat2 = math.radians(lat2)
lon2 = math.radians(lon2)
dlon = lon2 - lon1
dlat = lat2 - lat1
a = math.sin(dlat / 2)**2 + math.cos(lat1) * math.cos(lat2) * math.sin(dlon / 2)**2
c = 2 * math.atan2(math.sqrt(a), math.sqrt(1 - a))
return R * c
df_features = collections.OrderedDict([])
df_features['distance_to_kremlin'] = df_zones.apply(
lambda row: dist_calc(row.lat_c, row.lon_c, kremlin_lat, kremlin_lon), axis=1)
# набор фильтров точек, по которым будет считаться статистика
POINT_FEATURE_FILTERS = [
('tagged', lambda
node: len(node.tags) > 0),
('railway', lambda node: node.tags.get('railway') == 'station'),
('shop', lambda node: 'shop' in node.tags),
('public_transport', lambda node: 'public_transport' in node.tags),
]
# центры квадратов в виде матрицы
X_zone_centers = df_zones[['lat_c', 'lon_c']].as_matrix()
for prefix, point_filter in POINT_FEATURE_FILTERS:
# берем подмножество точек в соответствии с фильтром
coords = np.array([
[node.lat, node.lon]
for node in tagged_nodes
if point_filter(node)
])
# строим структуру данных для быстрого поиска точек
neighbors = NearestNeighbors().fit(coords)
# признак вида "количество точек в радиусе R от центра квадрата"
for radius in [0.001, 0.003, 0.005, 0.007, 0.01]:
dists, inds = neighbors.radius_neighbors(X=X_zone_centers, radius=radius)
df_features['{}_points_in_{}'.format(prefix, radius)] = np.array([len(x) for x in inds])
# признак вида "расстояние до ближайших K точек"
for n_neighbors in [3, 5, 10]:
dists, inds = neighbors.kneighbors(X=X_zone_centers, n_neighbors=n_neighbors)
df_features['{}_mean_dist_k_{}'.format(prefix, n_neighbors)] = dists.mean(axis=1)
df_features['{}_max_dist_k_{}'.format(prefix, n_neighbors)] = dists.max(axis=1)
df_features['{}_std_dist_k_{}'.format(prefix, n_neighbors)] = dists.std(axis=1)
# признак вида "расстояние до ближайшей точки"
df_features['{}_min'.format(prefix)] = dists.min(axis=1)
# Создаем таблицу и сохраняем ее в features.csv
df_features = pandas.DataFrame(df_features, index=df_zones.index)
df_features.to_csv('data/features.csv')
df_features.head()В итоге для каждого квадрата из обучающей и тестовой выборки имеем признаковое описание, которое можно использовать для предсказания. Небольшой модификацией предложенного кода можно учесть в признаках объекты других типов. Участники могут добавлять свои признаки, тем самым давая модели больше информации о городской застройке.
Предсказание числа вызовов
Опытные участники соревнований по анализу данных знают, что для получения высокого места важно не только смотреть на публичный лидерборд, но и делать собственную валидацию на тренировочной выборке. Сделаем простое разбиение тренировочной части выборки на подвыборки для обучения и валидации в соотношении 70/30.
Возьмем только целевые квадраты и обучим модель случайного леса (RandomForestRegressor) предсказывать среднее число вызовов в день.
Выделение валидационной подвыборки и обучение RandomForest
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor
df_zones_train = df_zones.query('is_test == 0 & is_target == 1')
idx_train, idx_valid = train_test_split(df_zones_train.index, test_size=0.3)
X_train = df_features.loc[idx_train, :]
y_train = df_zones.loc[idx_train, 'calls_daily']
model = RandomForestRegressor(n_estimators=100, n_jobs=4)
model.fit(X_train, y_train)Оценим качество на валидационной подвыборке, для всех дней недели построим одинаковый прогноз. Метрика качества — непараметрический коэффициент корреляции Кендалла tau-b, он реализован в пакете SciPy в виде функции scipy.stats.kendalltau.
Получается Validation score: 0.656881482683
Это неплохо, т.к. значение метрики 0 означает отсутствие корреляции, а 1 — полное монотонное соответствие реальных значений и предсказанных.
Прогноз и оценка качества на валидации
from scipy.stats import kendalltau
X_valid = df_features.loc[idx_valid, :]
y_valid = df_zones.loc[idx_valid, 'calls_daily']
y_pred = model.predict(X_valid)
target_columns = ['calls_wd{}'.format(d) for d in range(7)]
df_valid_target = df_zones.loc[idx_valid, target_columns]
df_valid_predictions = pandas.DataFrame(collections.OrderedDict([
(column_name, y_pred)
for column_name in target_columns
]), index=idx_valid)
df_comparison = pandas.DataFrame({
'target': df_valid_target.unstack(),
'prediction': df_valid_predictions.unstack(),
})
valid_score = kendalltau(df_comparison['target'], df_comparison['prediction']).correlation
print('Validation score:', valid_score)До вхождения в ряды участников, которые получат приглашение на Data Fest, остается один небольшой шаг: построить таблицу с предсказаниями на всех тестовых квадратах и отправить их в систему.
Построение предсказаний на тесте
idx_test = df_zones.query('is_test == 1').index
X_test = df_features.loc[idx_test, :]
y_pred = model.predict(X_test)
df_test_predictions = pandas.DataFrame(collections.OrderedDict([
(column_name, y_pred)
for column_name in target_columns
]), index=idx_test)
df_test_predictions.to_csv('data/sample_submission.csv')
df_test_predictions.head()Зачем анализировать геоданные?
Основными источниками данных, не только пространственных (географических), но и временных, для любой телеком-компании являются расположенные на всей территории стран обслуживания комплексы аппаратуры для приема и передачи сигнала — Базовые Станции (БС). Пространственный анализ данных труднее технически, но может принести существенную пользу и получить признаки, добавляющие весомый вклад в эффективность моделей машинного обучения.
В компании МТС использование географических данных помогает расширить базу знаний. Они могут использоваться для повышения качества предоставляемого сервиса при анализе жалоб абонентов на качество связи, улучшения зоны покрытия сигнала связи, планирования развития сети и решения других задач, где пространственно временная связь является важным фактором.
Возрастающая, особенно в крупных городах, плотность населения, стремительное развитие объектов инфраструктуры и дорожной сети, космические снимки и векторные карты, количество строений и POI (points of interest) с открытых карт местности, связанных с оказание сервисных услуг – все эти пространственные данные можно получить из внешних источников. Такие данные могут применяться как дополнительный источник информации, а также позволят получить объективную картину вне зависимости от покрытия сети.
Понравилась задача? Тогда мы приглашаем вас принять участие в онлайн-хакатоне по анализу географических данных Geohack.112. Регистрируйтесь и загружайте свои решения на сайт до 24 апреля. Авторы трех лучших результатов получат денежные призы. Отдельные номинации предусмотрены для участников, представивших лучшее публичное решение задачи и лучшую визуализацию журналистики данных. Общий призовой фонд МТС GeoHack — 500 000 рублей. Мы надеемся увидеть новые интересные подходы к генерации пространственных фичей, визуализации геоданных и использования новых открытых источников информации.
Награждение победителей пройдет 28 апреля на конференции DataFest.

