Приветствую всех читателей. Сегодня попробую продолжить серию достаточно редких статей, посвящённым естественным алгоритмам. В частности, эта статья будет посвящена модификации муравьиного алгоритма, известной как Max-Min Ant System (MMAS). Я расскажу об отличиях от классического муравьиного алгоритма и о причинах внесения таких модификаций. Подробности под катом.
Несколько лет назад на Хабре была опубликована статья «Муравьиные алгоритмы», в ней достаточно подробно описан оригинальный муравьиный алгоритм Дориго (Dorigo). Тем, кто не знаком с алгоритмом, рекомендую прочитать эту статью, в ней, к слову, перечислен целы ряд модификаций алгоритма. Теперь немного об обещанном MMAS-алгоритме для задачи о коммивояжере.
Алгоритм MMAS является своеобразной надстройкой над алгоритмом ACO (Ant Colony Optimization, Dorigo and Stutzle, 2004). Согласно алгоритму ACO, муравьи являются независимыми агентами и взаимодействуют между собой только через феромон размещённый на путях следования муравьёв (на рёбрах графа). При первом запуске на каждое ребро наносится начальное количество феромона, которое потом изменяется в зависимости от того, как часто муравьи проходят по рёбрам количество феромона изменяется по формуле:
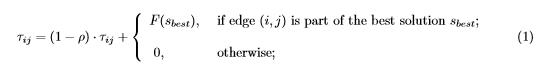
р — коэффициент испарения феромона, F — величина, обратная стоимости лучшего решения. И, собственно, модификация алгоритма: количество феромона лежит в промежутке .
.
Далее, чтобы обеспечить муравьям возможность побывать даже на самых непривлекательных рёбрах применяется следующая формула из классического муравьиного алгоритма:

Для читателей, знакомых с муравьиным алгоритмом, ничего нового в этой формуле быть не должно, остальных же снова отправляю почитать статья о классическом алгоритме.
Теперь добавим ещё одну модификацию предложенную Дориго и Гамбарделло (Dorigo and Gambardella, 1997).

Здесь поясню чуть более подробно. Для сохранения лучшего пути в графе используются «жадные» муравьи. Их доля в общем числе муравьёв равна q, то есть путь, по которому пройдёт муравей определяется по формуле (3). Вершина, в которую муравей пойдёт дальше выбирается из всех смежных не посещённых вершин так, чтобы её привлекательность была наибольшей. Соответственно 0 < q < 1 — вероятность того, что текущий муравей жадный, а с вероятностью 1 — q муравей ведёт себя стандартным образом. Коэффициент q, как и все остальные, определяется экспериментально.
Модификация, связанная с ограничением феромона, как и сам алгоритм, очень хорошо вписывается в естественные законы природы. Интуитивно понятно, что количество феромона в реальных условия не может расти постоянно. В какой-то момент скорость испарения феромона сравняется со скоростью обновления феромонного следа, а скорость изменения количества феромона не постоянна, однако использование такой функции очень сильно увеличит время выполнения, поэтому оптимально просто установить максимальное значение количества феромона. Аналогичная ситуация и с нижней планкой количества феромона. При этом значения ограничений влияют на эффективность алгоритма и, как вы уже догадались, подбираются экспериментально.
Спасибо за внимание.
Dorigo M., Stutzle T. (2004) Ant Colony Optimization. MIT Press, Cambridge, MA
Pellegrini P., Stutzle T, and Birattari M. (2011) A Critical Analysis of Parameter Adaptation in Ant Colony Optimization. IRIDIA – Technical Report Series
Вместо предисловия
Несколько лет назад на Хабре была опубликована статья «Муравьиные алгоритмы», в ней достаточно подробно описан оригинальный муравьиный алгоритм Дориго (Dorigo). Тем, кто не знаком с алгоритмом, рекомендую прочитать эту статью, в ней, к слову, перечислен целы ряд модификаций алгоритма. Теперь немного об обещанном MMAS-алгоритме для задачи о коммивояжере.
Идея
Алгоритм MMAS является своеобразной надстройкой над алгоритмом ACO (Ant Colony Optimization, Dorigo and Stutzle, 2004). Согласно алгоритму ACO, муравьи являются независимыми агентами и взаимодействуют между собой только через феромон размещённый на путях следования муравьёв (на рёбрах графа). При первом запуске на каждое ребро наносится начальное количество феромона, которое потом изменяется в зависимости от того, как часто муравьи проходят по рёбрам количество феромона изменяется по формуле:
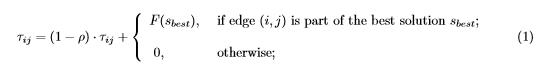
р — коэффициент испарения феромона, F — величина, обратная стоимости лучшего решения. И, собственно, модификация алгоритма: количество феромона лежит в промежутке
 .
.Далее, чтобы обеспечить муравьям возможность побывать даже на самых непривлекательных рёбрах применяется следующая формула из классического муравьиного алгоритма:

Для читателей, знакомых с муравьиным алгоритмом, ничего нового в этой формуле быть не должно, остальных же снова отправляю почитать статья о классическом алгоритме.
Теперь добавим ещё одну модификацию предложенную Дориго и Гамбарделло (Dorigo and Gambardella, 1997).

Здесь поясню чуть более подробно. Для сохранения лучшего пути в графе используются «жадные» муравьи. Их доля в общем числе муравьёв равна q, то есть путь, по которому пройдёт муравей определяется по формуле (3). Вершина, в которую муравей пойдёт дальше выбирается из всех смежных не посещённых вершин так, чтобы её привлекательность была наибольшей. Соответственно 0 < q < 1 — вероятность того, что текущий муравей жадный, а с вероятностью 1 — q муравей ведёт себя стандартным образом. Коэффициент q, как и все остальные, определяется экспериментально.
Пояснение
Модификация, связанная с ограничением феромона, как и сам алгоритм, очень хорошо вписывается в естественные законы природы. Интуитивно понятно, что количество феромона в реальных условия не может расти постоянно. В какой-то момент скорость испарения феромона сравняется со скоростью обновления феромонного следа, а скорость изменения количества феромона не постоянна, однако использование такой функции очень сильно увеличит время выполнения, поэтому оптимально просто установить максимальное значение количества феромона. Аналогичная ситуация и с нижней планкой количества феромона. При этом значения ограничений влияют на эффективность алгоритма и, как вы уже догадались, подбираются экспериментально.
Спасибо за внимание.
Литература
Dorigo M., Stutzle T. (2004) Ant Colony Optimization. MIT Press, Cambridge, MA
Pellegrini P., Stutzle T, and Birattari M. (2011) A Critical Analysis of Parameter Adaptation in Ant Colony Optimization. IRIDIA – Technical Report Series


iroln
Ну хорошо, а где можно использовать этот алгоритм на практике? Чем он лучше/хуже других эвристических методов оптимизации или того же Direct search? В статье не хватает примеров практического применения и сравнения с другими методами.
AndrewNikolaevich Автор
Алгоритм применяется для решения задач TSP (travelling salesman problem) и QAP (Quadratic assignment problem), к которым сводится достаточно много практических задач, (решение TSP, например, широко применяется в проектах связанных с грузоперевозками и тому подобным, а QAP в проектах с планированием). Сравнения с другими алгоритмами и, возможно, исходные коды будут позднее.