Путём трудных геометрических подсчётов Филип Гиббс обнаружил наименьшее из известных покрытий для любой возможной формы

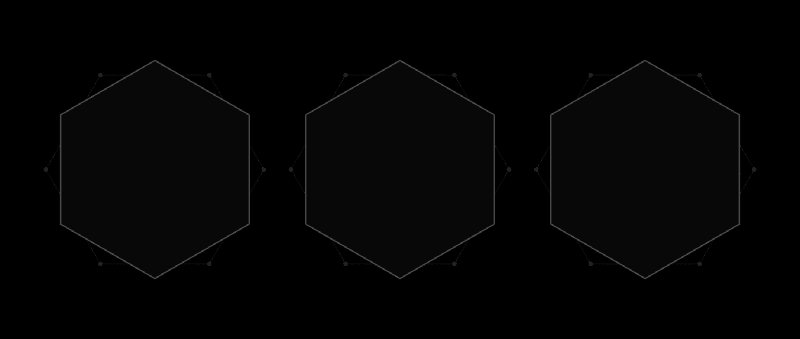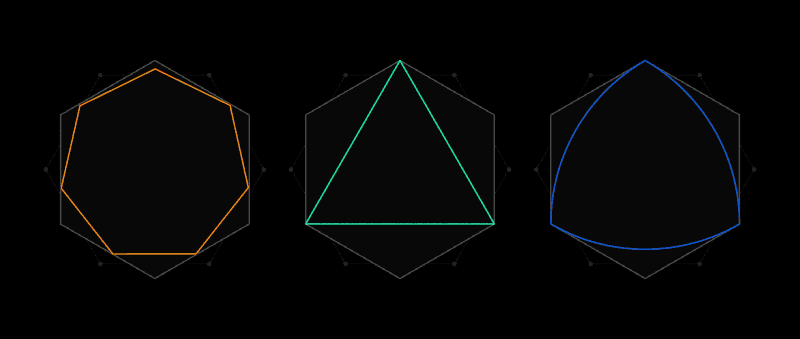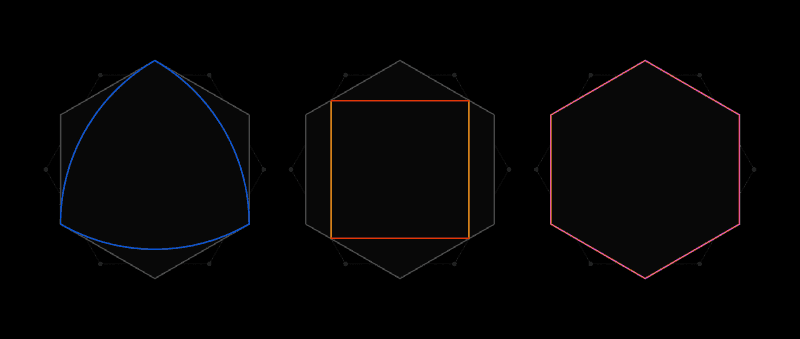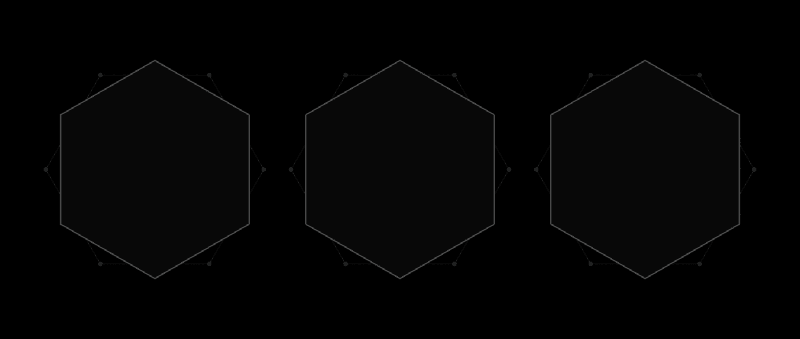
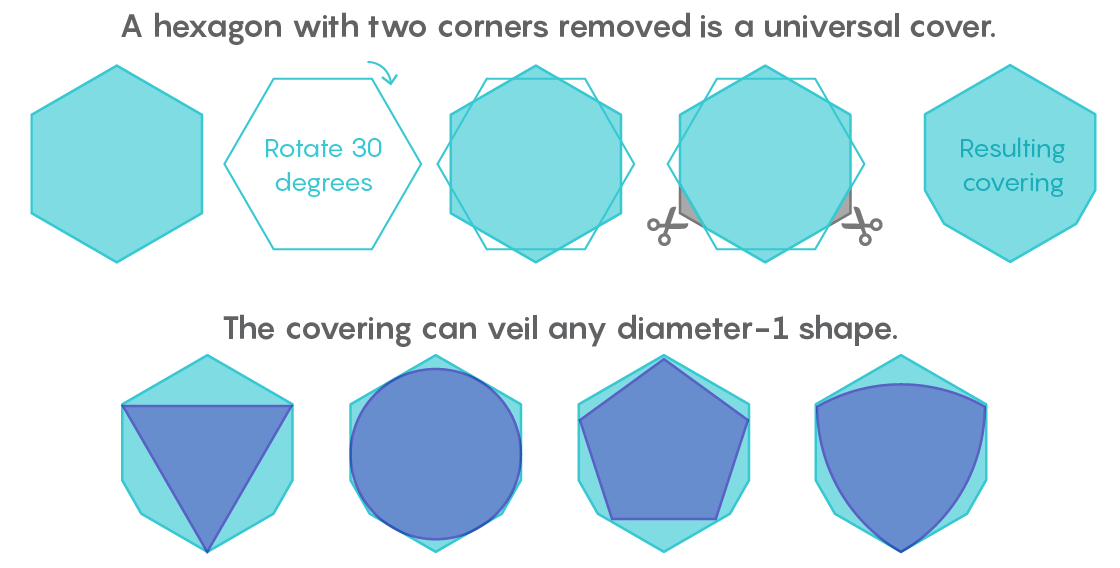
Такое универсальное покрытие, как шестиугольник, можно описать вокруг любой формы

Филип Гиббс – не профессиональный математик. Поэтому когда ему хотелось поразмышлять над какой-либо задачей, он искал такую, с которой может справиться и любитель. Он обнаружил трудную задачу, которая может свести с ума даже лучшие умы. И в работе, опубликованной в этом году, Гиббс значительно продвинулся в решении вопроса столетней давности, зависящего от способности точно измерять площадь вплоть до атомных масштабов.

Первым эту задачу предложил французский математик Анри Леон Лебег, в письме к своему другу Юлиусу Палу, написанному в 1914 году. Лебег спросил: какова форма наименьшей возможной площади, способной полностью покрыть большое количество других форм (имеющих одно общее свойство, о котором ниже)?

За прошедший век задача поиска универсального покрытия превратилась в мышеловку: прогресс в её решении, если и происходил периодически, всегда был потрясающе малым. Улучшение Гиббса по сравнению с этим стало кардинальным – хотя над ним всё равно нужно немного подумать.

Представьте себе десяток бумажных вырезок различного размера и форм, лежащих у вас на полу. Теперь представьте, что вам предлагают придумать ещё одну форму, достаточно большую для того, чтобы накрыть любую из имеющихся. Путём экспериментов – накладывая формы и поворачивая их – можно придумать какой-то способ решить эту задачу. Но, найдя универсальное покрытие, можно ли быть уверенным, что вы нашли наименьшее? Можно представить, что вы в течение дня периодически возвращаетесь к своей форме, и находите возможность срезать дополнительные кусочки то тут, то там.

Таков дух задачи Лебега об универсальном покрытии. Вместо бумажных вырезок в ней рассматриваются формы, у которых две любые точки отстоят друг от друга не далее, чем на одну единицу длины. Самой очевидной формой будет круг диаметра 1, однако их существует бесконечное количество: равносторонний треугольник, правильный пятиугольник, правильный шестиугольник, трёхсторонняя форма с пухлыми боками, известная, как треугольник Рёло – и это только для начала. Разнообразие форм затрудняет поиск наименьшего покрытия их всех.



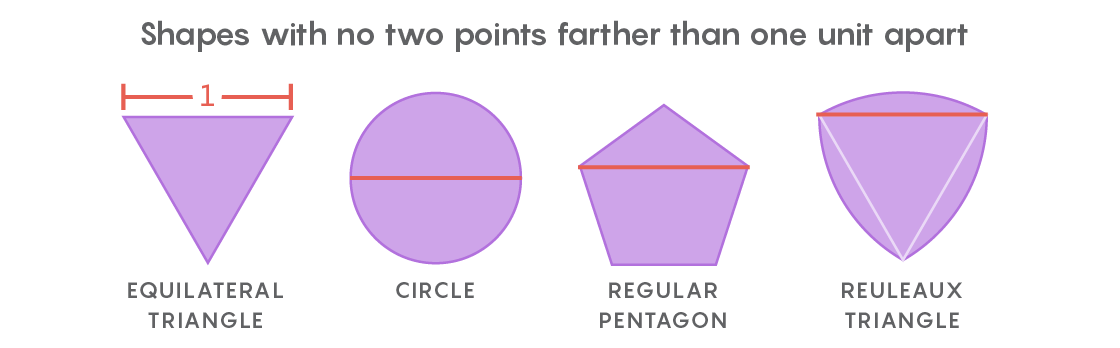
Вскоре после получения письма от Лебега, Пал понял, что универсальным покрытием будет правильный шестиугольник. А затем он улучшил этот результат, заметив, что срезав два уголка шестиугольника, не стоящие рядом, можно получить форму с меньшей площадью, которая всё равно окажется универсальным покрытием.

«Берём шестиугольник, кладём второй поверх него, поворачиваем на 30 градусов, и отрезаем два угла. На этом Пал закончил изыскания», — сказал Гиббс.

В следующие 80 лет два других математика отрезали узкие полоски от универсального покрытия Пала. В 1936 Роланд Спрэг удалил небольшую часть рядом с одним из углов. В 1992 Хэнсен удалит два миниатюрных клинышка из нижнего правого и левого углов. Иллюстрации Хэнсена могли передать расположение этих частей, но не их размер: их площадь составляла 0,00000000004 единицы.



«В масштабе их не нарисуешь, они были бы размером с атом», — сказал Джон Баез, математик из Калифорнийского университета в Риверсайде.

Баез вывел задачу Лебега из забвения, когда написал о ней в своём блоге о популярной математике в 2013 году. Он признался, что он был заворожён этой задачей так, как вас может заворожить видео с тонущим насекомым. «Мой интерес к задаче был нездоровым, — писал БАез. – Мне неизвестны причины, по которой она может быть важной. Я не вижу, как она может соединяться с множеством других прекрасных задач. Она просто кажется невероятно сложной по сравнению с первым впечатлением. Я восхищаюсь работающими над ней людьми так же, как восхищаюсь людьми, решившими пересечь Антарктиду на лыжах».

Филип Гиббс никогда не пересекал Антарктиду на лыжах, но читал блог Баеза. Когда он встретил запись о задаче Лебега, то подумал: «Вот, это именно то, что мне нужно».

Атомные ножницы

Когда-то Гиббс думал, что может стать учёным. Он получил диплом по математике в Кембриджском университете и защитил докторскую по теоретической физике в Университете Глазго. Однако вскоре утерял энтузиазм к академическим исследованиям и стал программистом. Он работал над системами, предназначенными для разработки судов, управления воздушным трафиком и финансами, а в 2006-м ушёл на пенсию.

У Гиббса остался интерес к академическим вопросам, но в качестве непрофессионального исследователя он мало что мог сделать. «Независимому учёному тяжело отслеживать всё происходящее, — сказал он. – Но если найти правильную нишу, можно что-то сделать, и получить какие-то полезные результаты».


Математик-любитель Филип Гиббс

Такой нишей оказалась задача Лебега об универсальном покрытии. Эта задача никогда не пользовалась вниманием математиков, поэтому он подозревал, что сможет достичь какого-то прогресса. Гиббс также понял, что его опыт в программировании может стать преимуществом. «Я всегда выискиваю задачи, в решении которых можно использовать компьютеры и экспериментальную математику», — сказал он.

В 2014 году Гиббс прогнал компьютерную симуляцию для 200 случайных форм диаметра 1. Из симуляций следовало, что у него может получиться отрезать небольшой кусочек от верхнего угла предыдущего наименьшего покрытия. Он превратил это в доказательство того, что новое покрытие будет работать для всех возможных форм диаметра 1. Гиббс отправил доказательство Баезу, который совместно с одним из своих студентов, Кариной Багдасарян, помог Гиббсу придать работе формальный математический стиль.

Они втроём опубликовали работу в интернете в феврале 2015. Она уменьшала площадь наименьшего возможного универсального покрытия с 0,8441377 до 0,8441153 единиц. Экономия в 0,0000224 единицы была почти в миллион раз больше, чем то, чего добился Хансен в 1992-м.

Гиббс был уверен, что сможет улучшить результат. В работе, опубликованной в октябре, он отрезал ещё один относительно крупный кусок от универсального покрытия, доведя его площадь до 0,84409359 единиц.



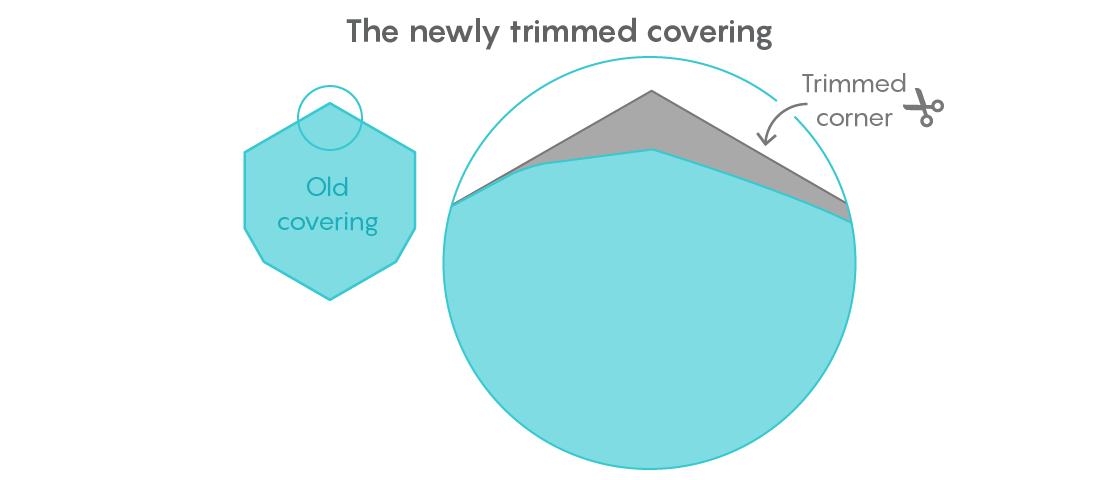
Его стратегией было переместить все формы диаметром 1 в угол универсального покрытия, обнаруженного им несколько лет назад, а затем удалить всю оставшуюся площадь противоположного угла. Но точное измерение сэкономленной площади оказалось трудным делом. Техники, использованные Гиббсом, были основаны на евклидовой геометрии, но были выполнены с такой точностью, которая потрясла бы любого ученика старших классов.

«С точки зрения математики, это всё геометрия для старших классов. Но выполняемая с фанатичной напряжённостью», — писал Баез.

Пока что Гиббс удерживает первое место в поисках наименьшего универсального покрытия, но его приз находится в опасности. Гиббс считает, что есть возможность найти покрытие ещё меньшего размера. Баез надеется, что внимание, которое Гиббс вернул к задаче Лебега, стимулирует интерес других математиков. Возможно, уже пора оставить в стороне линейку и циркуль и задействовать весь арсенал современной математики.

«Возможно, что правильный способ решения этой загадки будет использовать совершенно другие идеи, — сказал он, — хотя я представления не имею, какие идеи это могут быть».