Планиметрия изучется в начальном курсе геометрии и зачастую сводится к решению практических задач без изучения теоретической базы.
В данной статье приводятся альтернативные (подсказкам) решения некоторых задач приложения Euclidea (геометрические построения с помощью циркуля и линейки).
Статья предназначена для тех, кто интересуется планиметрией.
Решения задач 1.1, 1.2 и 1.3 основаны на том, что с помощью циркуля и линейки можно построить равносторонний треугольник.
1.1 Построить угол 60° с заданой стороной.
1.2 Построить серединный перпендикуляр к отрезку
Рассмотрим Предложение I, приведённое в «Началах» Евклида
Такой треугольник строится на пересечении двух окружностей одного диаметра.
Доказательство того, что этот треугольник является равноcторонним приводится далее в Предложении I «Начал»
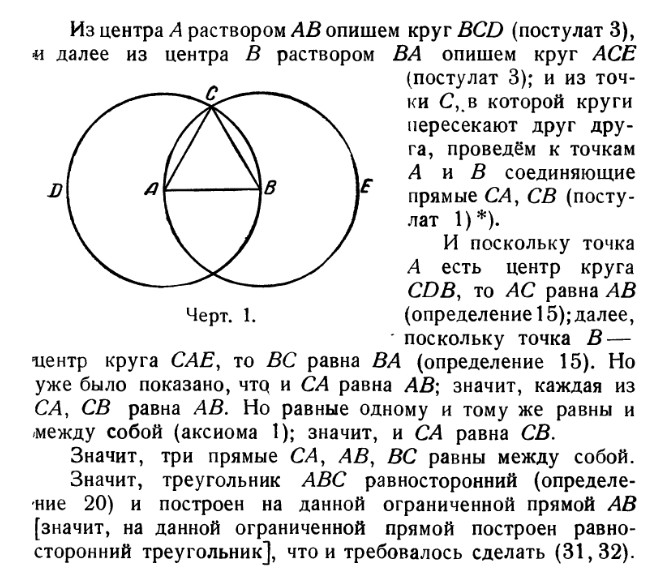
1.3 Найти середину отрезка
Эту задачу можно решить, используя построения из предыдущей задачи, но, вообще, теорема Мора-Маскерони гласит, что
Рассмотрим сперва задачу 4.1 Удвоенный отрезок
В книге Я. Перельмана «Занимательная геометрия» приводится решение этой задачи
Далее необходимо построить равнобедренный треугольник с основанием, равным r и длинами боковых сторон, равными 2r.

AEF — равнобедренный треугольник с основанием, равным r и длинами боковых сторон, равными 2r.
AFM — равнобедренный треугольник с основанием, равным r/2 и длинами боковых сторон, равными r.
Ссылка на источник
Решение методом Штейнера-Понеселе
Решим вспомогательную задачу:
Провести прямую, паралельную данному отрезку.
Решение:

Далее в приложении есть похожая задача 5.1 Параллельная прямая через точку; построения, используемые для решения задачи 5.1 можно использовать для решения задачи 1.3
Далее, решим Задачу 1 из параграфа 3 книги «Геометрические построения на плоскости» (Б.И. Аргунов, М.Б. Балк.)
Задача 1: Даны две параллельные прямые а и b и на одной из них, например a, отрезок AB. Построить середину этого отрезка.
Для решения нам понадобится одно вспомогательное предложение («лемма о трапеции»):
Прямая, соединяющая точку пересечения диагоналей трапеции с точкой пересечения продолженных её боковых сторон, делит оба основания трапеции пополам.
Далее в книге приводится д-во, которое я приводить не буду
Решение:
Изберем произвольную точку P, лежащую вне полосы, ограниченной заданными прямыми

Проведем прямые PA и PB и отметим точки D и C их пересечения прямой b. Пусть О — точка пересечения прямых AC и BD. Тогда, согласно предыдущей лемме, прямая PO пересечёт отрезок AB в его середине M.
Решением задачи 1.3 по методу Штейнера-Понеселе будет:

1.4 Окружность, вписанная в квадрат
Постройте окружность, вписанную в квадрат.
Решим вспомогательную задачу
2.6 Опустить перпендикуляр
Эта задача есть в книге «Занимательная геометрия»
Т.о., задачу 1.4 можно решить, опустив перпендикуляр из точки пересечения диагоналей квадрата на одну из его сторон.
Это же построение можно использовать для решения задачи 2.9 Окружность, касающаяся прямой
1.6 Найти центр окружности.
Центр окружности можно найти, построив диаметр этой окружности и разделив его пополам, а для построения диаметра можно воспользоваться, например, теоремой Фалеса об угле, опирающемся на диаметр окружности

Построим две хорды, лежащие под прямым углом друг к другу; соединим противоположные концы хорд

Для решения задачи полученный диаметр надо разделить пополам.
Далее, диаметр можно построить, проведя касательную к окружности и построив перпендикуляр к касательной в точке касания.
Рассмотрим задачи 2.7 и 2.8
2.7 Восстановить перпендикуляр
Эту задачу можно решить, например, так

Это построение можно использовать и для решения задачи 3.5
2.8 Касательная к окружности в точке
Предположим, что нам известен центр окружности.
Тогда задачу можно решить, построив равносторонний треугольник с длиной ребра, равной 2r и вершиной, лежашей в центре исходной окружности. Тогда касательной к окружности будет одна из биссектрис/медиан/высот треугольника.

Касательная может представлять из себя основание равнобедренного треугольника

Оказывается, такой равнобедренный треугольник можно построить без привязки к центру окружности

Следовательно, задачу 1.6 можно решить, проведя касательную к окружности в произвольной точке и построив перпендикуляр к касательной в этой точке. Затем разделить полученный диаметр пополам.
1.7 Квадрат, вписанный в окружность.
В книге «Занимательная геометрия» рассматривается аналогичная этой задаче

Построения, ведущие к решению задачи 1.7 методом Мора-Маскерони будут такими

В приложении нет такой операции, как перенос раствора циркуля, поэтому необходимо использовать дополнительные построения.
На рисунке видно, что вертикальная прямая проходит через точки пересечения окружностей. Для переноса раствора необходимо разделить один из сегментов прямой пополам, как в задаче 1.3
P.S. Ксати, у создателей приложения есть своя группа в VK vk.com/euclidea
В данной статье приводятся альтернативные (подсказкам) решения некоторых задач приложения Euclidea (геометрические построения с помощью циркуля и линейки).
Статья предназначена для тех, кто интересуется планиметрией.
Решения задач 1.1, 1.2 и 1.3 основаны на том, что с помощью циркуля и линейки можно построить равносторонний треугольник.
1.1 Построить угол 60° с заданой стороной.
1.2 Построить серединный перпендикуляр к отрезку
Рассмотрим Предложение I, приведённое в «Началах» Евклида
На данной ограниченной прямой построить равносторонний треугольник
Такой треугольник строится на пересечении двух окружностей одного диаметра.
Доказательство того, что этот треугольник является равноcторонним приводится далее в Предложении I «Начал»

1.3 Найти середину отрезка
Эту задачу можно решить, используя построения из предыдущей задачи, но, вообще, теорема Мора-Маскерони гласит, что
всё, что можно построить с помощью циркуля и линейки, может быть построено с помощью одного циркуля.
Рассмотрим сперва задачу 4.1 Удвоенный отрезок
В книге Я. Перельмана «Занимательная геометрия» приводится решение этой задачи
Из точки В радиусом АВ описываем окружность.
По этой окружности откладываем от точки А расстояние АВ три раза: получаем точку С, очевидно, диаметрально противопротивоположную А. Расстояние АС представляет собой двойное расрасстояние АВ. Проведя окружность из С радиусом ВС, мы можем таким же образом найти точку,
диаметрально противоположную В и, следовательно, удаленную от А на
тройное расстояние АВ, и т. д.
Далее необходимо построить равнобедренный треугольник с основанием, равным r и длинами боковых сторон, равными 2r.

AEF — равнобедренный треугольник с основанием, равным r и длинами боковых сторон, равными 2r.
AFM — равнобедренный треугольник с основанием, равным r/2 и длинами боковых сторон, равными r.
Ссылка на источник
Решение методом Штейнера-Понеселе
Теорема Штейнера — Понселе — теорема из области геометрических построений, утверждающая, что любое построение, выполнимое на плоскости циркулем и линейкой, можно выполнить одной линейкой, если нарисована хотя бы одна окружность и отмечен её центр.
Решим вспомогательную задачу:
Провести прямую, паралельную данному отрезку.
Решение:

Далее в приложении есть похожая задача 5.1 Параллельная прямая через точку; построения, используемые для решения задачи 5.1 можно использовать для решения задачи 1.3
Далее, решим Задачу 1 из параграфа 3 книги «Геометрические построения на плоскости» (Б.И. Аргунов, М.Б. Балк.)
Задача 1: Даны две параллельные прямые а и b и на одной из них, например a, отрезок AB. Построить середину этого отрезка.
Для решения нам понадобится одно вспомогательное предложение («лемма о трапеции»):
Прямая, соединяющая точку пересечения диагоналей трапеции с точкой пересечения продолженных её боковых сторон, делит оба основания трапеции пополам.
Далее в книге приводится д-во, которое я приводить не буду
Решение:
Изберем произвольную точку P, лежащую вне полосы, ограниченной заданными прямыми

Проведем прямые PA и PB и отметим точки D и C их пересечения прямой b. Пусть О — точка пересечения прямых AC и BD. Тогда, согласно предыдущей лемме, прямая PO пересечёт отрезок AB в его середине M.
Решением задачи 1.3 по методу Штейнера-Понеселе будет:

1.4 Окружность, вписанная в квадрат
Постройте окружность, вписанную в квадрат.
Решим вспомогательную задачу
2.6 Опустить перпендикуляр
Эта задача есть в книге «Занимательная геометрия»
Из точки A, лежащей вне данной полуокружности, опустить на её диаметр перпендикуляр, обходясь при этом без циркуля. Положение центра полуокружности не указано.
Нам пригодится здесь то свойство треугольника, что все его высоты пересекаются в одной точке. Соединим A с B и C; получим точки D и E. Прямые BE и CD, очевидно, — высоты треугольника ABC. Третья высота — искомый перпендикуляр к BC — должна проходить через пересечение двух других, т.е. через точку M. Проведя по линейке прямую через точки A и M, мы выполним требованиек задачи, не прибегая к услугам циркуля.
Т.о., задачу 1.4 можно решить, опустив перпендикуляр из точки пересечения диагоналей квадрата на одну из его сторон.
Это же построение можно использовать для решения задачи 2.9 Окружность, касающаяся прямой
1.6 Найти центр окружности.
Центр окружности можно найти, построив диаметр этой окружности и разделив его пополам, а для построения диаметра можно воспользоваться, например, теоремой Фалеса об угле, опирающемся на диаметр окружности
Плоский угол, опирающийся на диаметр окружности, — прямой.

Построим две хорды, лежащие под прямым углом друг к другу; соединим противоположные концы хорд

Для решения задачи полученный диаметр надо разделить пополам.
Далее, диаметр можно построить, проведя касательную к окружности и построив перпендикуляр к касательной в точке касания.
Рассмотрим задачи 2.7 и 2.8
2.7 Восстановить перпендикуляр
Эту задачу можно решить, например, так

Это построение можно использовать и для решения задачи 3.5
2.8 Касательная к окружности в точке
Предположим, что нам известен центр окружности.
Тогда задачу можно решить, построив равносторонний треугольник с длиной ребра, равной 2r и вершиной, лежашей в центре исходной окружности. Тогда касательной к окружности будет одна из биссектрис/медиан/высот треугольника.

Касательная может представлять из себя основание равнобедренного треугольника

Оказывается, такой равнобедренный треугольник можно построить без привязки к центру окружности

Следовательно, задачу 1.6 можно решить, проведя касательную к окружности в произвольной точке и построив перпендикуляр к касательной в этой точке. Затем разделить полученный диаметр пополам.
1.7 Квадрат, вписанный в окружность.
В книге «Занимательная геометрия» рассматривается аналогичная этой задаче
Задача Наполеона

Построения, ведущие к решению задачи 1.7 методом Мора-Маскерони будут такими

В приложении нет такой операции, как перенос раствора циркуля, поэтому необходимо использовать дополнительные построения.
На рисунке видно, что вертикальная прямая проходит через точки пересечения окружностей. Для переноса раствора необходимо разделить один из сегментов прямой пополам, как в задаче 1.3
P.S. Ксати, у создателей приложения есть своя группа в VK vk.com/euclidea
Комментарии (7)

Zenitchik
12.12.2019 12:32А смысл статьи-то в чём? Ну да, есть задачи. Ну да, вот так они решаются. И что?

demsp Автор
12.12.2019 21:57В этом и смысл.

Zenitchik
13.12.2019 01:08Ваши решения ни на что не годны. Смысл игры в том, чтобы уложиться в указанные лимиты.
Задача 2.8 решается за 4Е на вскидку. С 11Е — лучше бы не позорились. (кто не играл: Е — это элементарное действие, построение прямой или окружности).
То же можно сказать об остальных задачах: они решаются проще.
Сложность игры в том, что самый очевидный способ решения — не укладывается в лимит, и приходится искать оптимизацию.





eugensk
Всё интересно. Только отметьте, что тут получается не диаметрально противопротивоположная точка, а какая-то более-менее в том районе, и это не решение задачи на построение:
trolley813
Тут получается именно диаметрально противопротивоположная точка — потому что сторона вписанного в окружность шестиугольника равна радиусу этой окружности (поскольку треугольник равносторонний получается (образованный 2 точками на окружности и центром), когда мы откладываем радиус, то это значит, центральный угол равен 60°, т.е. 360°/6. Умножаем на 3 раза, получается 180°).
eugensk
Упс, это я поспешил! Действительно, отмеряется же по прямой а не по дуге :) Позор мне.