Привет, Хабр!
В самом конце года успеваем поделиться с вами новостью о том, что приступаем к работе «Bayesian Statistics the Fun Way» от издательства No Starch Press. Предлагаем перевод развернутого интервью с автором книги; текст касается как самой книги, так и смежных с ней тем, и даже дополнительного чтения.

Я, как и большинство разрабов, интересуюсь сразу множеством вещей: функциональным программированием, операционными системами, системами типов, распределенными системами и наукой о данных. Вот почему я так воодушевился, узнав, что Уилл Курт, автор книги Get Programming with Haskell, написал книгу по байесовской статистике, которая вышла в издательстве No Starch Press. Найдется не так много людей, пишущих книги на разные темы. Я уверен, что Уиллу есть чем поделиться с читателями в своей новой книге – и не разочаровался в ней. Книга – отличный вводный материал, специально для тех, кому не поздоровилось с суровой математикой, но все равно хочется чего-то добиться в области Data Science. Новую книгу Курта я рекомендую читать после Think Stats, но до «Вероятностное программирование на Python: байесовский вывод и алгоритмы», Bayesian Analysis with Python и Doing Bayesian Data Analysis.
1. Зачем нужна еще одна книга по статистике?
Практически все из множества существующих в настоящее время книг по байесовской статистике предполагают, что у читателя уже есть либо общие представления о статистике солидный базис в программировании. Поэтому в настоящее время байесовская статистика часто воспринимается как продвинутая альтернатива для классической (т.е. частотной) статистики. Таким образом, хотя байесовская статистика и пользуется растущей популярностью, материалы по ней рассчитаны в основном на людей, уже имеющих хорошую количественную подготовку.
Когда человек решает попросту «изучить статистику», он берет вводную книгу, в которой статистика излагается с частотной точки зрения, дочитывает ее, наполовину разобравшись в куче тестов и правил и чувствует, что вся эта тема очень запутанная. Я хотел написать такую книгу по байесовской статистике, которую каждый может взять, прочитать и по прочтении получить интуитивное представление о том, каково мыслить статистически и как решать при помощи статистики реальные задачи. Я не вижу никаких причин, почему бы именно байесовская статистика не могла послужить первым вводным курсом в эту тему для абсолютного новичка.
Мне было бы очень приятно, если бы когда-нибудь при слове «статистика» люди стали подразумевать именно байесовскую статистику, а частотная статистика стала просто одной из академических ниш. Для этого нужно больше книг, в которых знакомство со статистикой для широкого круга читателей предлагалось бы именно с использованием байесовских методов, причем, автор учитывал, что это может быть самое первое знакомство читателя со статистикой.
Я сразу подумывал назвать эту книгу «Statistics the Fun Way» («Статистика – это здорово»), но полагал, что, скорее всего, получу ворох гневных писем от людей, купивших такую книгу для подготовки к вступительному экзамену по статистике – и обнаруживших, что речь там совсем про другое! Надеюсь, моя книга станет маленьким шагом к тому времени, когда на вступительных экзаменах станут спрашивать именно байесовскую статистику, и читать такую книгу будет целесообразно даже для тех, кто просто готовится к экзамену.
2. Какова целевая аудитория книги? Может ли читать ее человек без какого-либо математического бэкграунда?
Работая над «Байесовская статистика – это здорово», я стремился создать книгу, в принципе, понятную каждому, кто усвоил математику в объеме программы для старших классов. Даже если вы лишь смутно припоминаете алгебру, темп изложения в книге такой, что вы сможете за ней поспевать. Байесовская статистика требует самую малость математического анализа и тем более упрощается при небольшом сопровождении программным кодом, поэтому я добавил в книгу два приложения, в которых даны основы языка R. Этого материала достаточно, чтобы R послужил вам продвинутым калькулятором, а базовые идеи математического анализа изложены в таком объеме, чтобы вы разобрались со всеми примерами из этой книги, где речь заходит об интегралах. Однако, я обещаю, что для чтения книги не придется решать никаких задач из области математического анализа.
Притом, насколько я потрудился, стараясь максимально сократить тот багаж математических знаний, что нужны для чтения книги, вы, читая ее, постепенно начнете усваивать математический образ мышления. Если вы как следует понимаете математику, которой оперируете, то станете понимать ее еще лучше. Поэтому я не пытался уклоняться от реальной математики, а, скорее, шаг за шагом объясняю ее, так, чтобы вся математика постепенно стала казаться вам очевидной. Как и многие, я когда-то считал, что математика – запутанная наука, и работать с ней сложно. Со временем же я убедился, что при правильном подходе математика не доставляет почти никакого труда. Любая путаница в математике обычно возникает только из-за попыток слишком быстро пройти материал – из-за этого упускаются важные этапы, необходимые для правильного рассуждения.
3. Почему программист должен изучать теорию вероятности и статистику?
Я действительно считаю, что каждый должен в каком-то объеме изучить теорию вероятности и статистику, так как эти знания помогут судить о неопределенности, которая повсюду окружает нас в жизни. Что касается программиста, ему точно придется иметь дело с некоторыми типичными задачами, где полезно понимать статистику. Весьма вероятно, что, в какой-то период профессиональной карьеры вам придется писать код, в котором принимаются некоторые решения на основе априори нечетких факторов. Возможно, это будет измерение конверсии веб-страницы, генерация некой случайной награды в игре, случайное распределение пользователей по группам, либо даже считывание информации с какого-нибудь нечеткого датчика. Во всех этих случаях уверенное понимание теории вероятности вам очень поможет. Моя собственная практика показывает, что вероятностный подход очень помогает в отладке многих багов, которые сложно воспроизвести, либо отследить до сложной проблемы. Если оказывается, что баг обусловлен недостаточной памятью, то можно ли быть уверенным, что баг станет возникать чаще, если память еще сильнее урезать? Если сложный баг можно объяснить двояко, то какую возможность лучше исследовать первой? Во всех подобных случаях может помочь теория вероятности. Разумеется, расцвет машинного обучения и Data Science приводит к тому, что инженерам все чаще приходится иметь дело с такими задачами, где программирование предлагает непосредственную работу с вероятностями.
4. Можно ли вкратце описать разницу между частотным и байесовским подходом к теории вероятности?
В частотной трактовке вероятность интерпретируется как утверждение о том, как часто должно происходить событие при многократных попытках. Так, дважды подбросив монетку, следует ожидать, что она 1 раз выпадет орлом, поскольку у монетки две стороны, и на одной из них орел. В байесовской трактовке вероятность интерпретируется как некоторая характеристика наших знаний, в принципе, как продолжение логики. Вероятность выбросить монетку орлом равна 0,5 поскольку я не вижу причин, по которым орел должен выпадать чаще решки. Итак, в случае подбрасывания монетки оба подхода вполне работоспособны. Однако, когда речь заходит о таких вещах, как шансы вашей любимой команды выиграть кубок мира, фактор степени уверенности становится гораздо весомее. Это, кстати, еще и означает, что байесовская статистика выступает с утверждениями не о мире, а о нашем понимании мира. Поскольку каждый понимает мир немного по-своему, байесовская статистика помогает нам учесть эти различия в нашем анализе. Во многих отношениях байесовский анализ – это наука об эволюции мнений.
5. Почему основное внимание в книге уделено именно байесовскому подходу?
Есть множество по-настоящему веских философских оснований сосредоточиться именно на байесовской статистике, но я руководствовался совершенно практичной причиной: с байесовским подходом все становится логично. Опираясь на относительно небольшой набор интуитивно понятных правил, можно выработать решение практически для любой проблемы, которая может вам попасться. Вот почему байесовская статистика обладает такой силой и гибкостью, и вот почему она так легка в изучении. Думаю, байесовский способ рассуждения отлично подходит именно программистам. Вы не пытаетесь решить задачу при помощи импровизированных тестов, а рассуждаете над ней и постепенно приходите к действительно оправданному решению. В принципе, байесовская статистика – это и есть рассуждение. Вы соглашаетесь со статическим анализом, только если он подлинно логичен и представляется вам убедительным, а не потому, что ваш произвольный с виду тест выдает вам некоторое столь же ничем не подкрепленное значение. Кроме того, байесовская статистика позволяет усомниться в результате и с качественной точки зрения. В повседневной практике часто бывает так, что двум людям представлены одни и те же факты, но выводы у них получаются разные. Байесовская статистика позволяет формально смоделировать такое расхождение во мнениях, так, что мы можем сами проверить, какие факты понадобятся, чтобы мы изменили свою точку зрения. Не приходится верить изложенным на бумаге результатам из-за какого-то p-значения, вы верите им, так как они кажутся вам по-настоящему убедительными.
6. Как байесовская статистика соотносится с машинным обучением
Среди сходств между машинным обучением (в особенности, нейронными сетями) и байесовской статистикой, о которых мне доводилось размышлять – такое: в обеих этих дисциплинах математический анализ может крайне усложняться. В принципе, машинное обучение – это понимание и решение очень нетривиальных производных. Вы получаете функцию, а для нее – функцию потерь, затем (автоматически) вычисляете производную и пытаетесь следовать за ней, пока она не приведет вас к оптимальным параметрам. Многие ехидно отмечают, что обратное распространение – это всего лишь «цепное правило», но практически во всех сложных задачах, связанных с машинным обучением, оно применяется очень успешно.
Байесовская статистика – это другая грань математического анализа, связанная с решением по-настоящему сложных интегралов. Майкл Бетанкур, автор Stan, отлично заметил, что практически весь байесовский анализ связан с вычислением ожиданий, то есть, с вычислением интегралов. В результате байесовского анализа у вас остается апостериорное распределение, но как-либо воспользоваться им невозможно, не проинтегрировав его и не получив таким образом конкретный ответ. К счастью, никто не отпускает ехидных комментариев по поводу интегралов, так как все знают, что даже самый тривиальный интеграл довольно сложен. Вот как это афористично сформулировано в одноv из комиксов xkcd:
Вот в таком странном состоянии оказались сегодня машинное обучение и байесовская статистика: простейшие идеи математического анализа мы развиваем до такой степени сложности, какая только поддается вычислениям.
Эта взаимосвязь также подчеркивает один ключевой момент. Когда мы говорим о производных, мы ищем конкретную точку, относящуюся к функции. Так, если известно положение и время, то скорость – это производная, полагающая определить, когда вы двигались быстрее всего. Маленький шаг к прогрессу в МО – это когда вы вычислили единственную метрику лучше, чем кто бы то ни было. Интегрирование – это суммирование всего процесса. Опять же, если вы знаете место и время, то интеграл – это расстояние, он позволяет узнать, как далеко вы продвинулись. Байесовская статистика – это суммирование всего, что вы знаете о проблеме, но она позволяет вам не просто делать отдельные прогнозы, но и охарактеризовать степень уверенности в наших прогнозах, находящихся в широком наборе вариантов. Прогресс в области байесовской статистики – это понимание все более сложных информационных систем.
7. Если читатели захотят глубже познакомиться с темой книги, какие материалы (книги, курсы, блоги) вы им посоветуете?
Максимум вдохновения я почерпнул из книги И. Т. Джейнса “Probability Theory: the Logic of Science”. Втайне надеюсь, что моя книга «Байесовская статистика – это здорово» сможет стать аналогом его книги, но рассчитанным на широкий круг читателей. Работать с книгой Джейнса – задача не из легких, причем, в ней представлен весьма радикальный извод байесовской статистики. Обри Клейтон оказал читателям изрядную услугу, составив серию лекций по главам этой книги.
Разумеется, если вам понравится книга, то, вероятно, вам понравится и мой блог. В последнее время я не так много писал туда, так как писал книгу «Байесовская статистика – это здорово», а до этого «Get Programming with Haskell», но сейчас у меня уже голова ломится от идей, и далеко не все они посвящены строго байесовским темам. Как правило, я размышляю на какую-нибудь тему из области статистики/вероятности, и из этой идеи аккуратно выделываю новую статью для блога.
8. По вашему опыту, какая концепция из области теории вероятности/статистики особенно сложна для понимания?
Честно говоря, самое сложное – это интерпретация вероятностей. Люди в самом деле утратили веру во многих байесовских аналитиков, таких, как Нейт Силвер (и многие другие), когда те прогнозировали, что Хиллари Клинтон с вероятностью 80% выигрывает выборы 2016 года – а она проиграла. Люди сочли, будто их кто-то обманул, и все были неправы, но, на самом деле, вероятность 80% — это не так много. Если врач скажет мне, что мои шансы на выживание – 80%, то я серьезно занервничаю.
Как правило, эта проблема решается так: указываем на вероятности как таковые и заявляем, что они плохо подходят для выражения неопределенности. Чтобы справиться с таким неудобством, приходится использовать коэффициенты или отношения правдоподобия, либо какую-нибудь децибел-подобную систему, например, такую, как джейновская концепция «доказательств» (evidence). Однако, я, как следует поразмышляв о вероятностях достаточно долго, я пришел к выводу, что однозначно годного способа для выражения неопределенности не существует.
Суть проблемы в том, что каждый из нас в глубине души убежден, что в мире есть определенность. Даже опытных специалистов по теории вероятности гложет такое ощущение, что, может быть, если выполнить верный анализ, узнать нужные априорные данные, добавить в вашу иерархическую модель еще один уровень, то все у вас получится, и вы избавитесь от неопределенности или как минимум ее уменьшите. Вероятности отчасти привлекательны мне этим причудливым сочетанием двух этих факторов: стремлением осмыслить мир и признанием того, что, как бы вы ни старались, мир все равно чем-нибудь вас удивит.
9. Что вы думаете о p-значениях как о мере статистической значительности? Могли бы вкратце описать, что такое p-хакинг?
В случае с p-значениями две вещи часто понимаются неверно. Во-первых, разумный человек не будет пытаться отвечать на вопросы при помощи p-значений. Представьте, как выглядел бы следующий разговор на работе:
Менеджер: “Вы пофиксиили этот баг, как вам было поручено?”
Вы: “Ну, я более чем уверен, что не пофиксил его…”
Менеджер: “Если вы его пофиксили – пометьте, что пофиксили.”
Вы: “О, нет, я никак не могу утверждать, что пофиксил его …”
Менеджер: “Вы что же, собираетесь пометить его ‘не буду фиксить’?”
Вы: “Нет, нет, конечно же все совсем не так ”
p-значения многих путают, так как они по природе своей неясные. Байесовская статистика сообщает вам апостериорную вероятность, которая представляет собой положительный ответ на вопрос, сформулированный так, как вы хотите. В вышеприведенном диалоге байесианец говорит: «Я вполне уверен, что баг исправлен». Если менеджер хочет, чтобы вы ответили более уверенно, то байесианец может собрать дополнительную информацию и сказать: «Я, в принципе, уверен, что он исправлен».
Вторая проблема – это укоренившаяся привычка выбирать 0.05 в качестве какого-то волшебного, якобы осмысленного значения. Возвращаясь к предыдущему вопросу о понимании вероятностей, 5%-я вероятность того, что произойдет некоторое событие, еще не означает, что это событие редкое. 5%-я вероятность получить 20 очков будет у вас при броске 20-гранной кости. Однако, любой, кто играл в «Подземелья и драконы», знает, что это далеко не невозможно. За пределами РПГ бросок кости – не лучший инструмент, чтобы отличать истину от лжи.
Здесь мы и подходим к p-хакингу. Вообразите, что вы играете в «Подземелья и Драконы» вместе с друзьями – и вы бросили 20 двадцатигранных костей сразу. Затем вы указываете на ту единственную, на которой выпало 20 очков, и объявляете: «именно эту кость я и собирался бросать, а все остальные были тестовые». Формально вы действительно набрали 20 очков, но ведь это все равно жульничество, согласитесь. В этом и заключается сущность p-хакинга. Вы делаете анализ до тех пор, пока не найдете нечто «существенное», а затем заявляете, что именно это вы и искали с самого начала.
10. Заключительные рекомендации о том, какую книгу лучше прочесть после вашей?
Теперь, когда работа над книгой закончена, я понемногу могу начинать наверстывать время и читать те книги, которые не успел прочесть, пока работал над собственной. Мне очень нравится «Bayesian Analysis with Python» Освальдо Мартина (знаю, недавно он давал интервью Not Monad Tutorial). Это отличная книга, в которой байесовский анализ рассматривается сквозь призму PyMC3. Мир вероятностного программирования в самом деле кажется мне очень увлекательным, и он будет все более и более становиться существенной составляющей практической байесовской статистики. Еще одна книга, которую я очень хочу прочитать — “Statistical Rethinking” Ричарда Макэльрита. Вскоре у нее выходит второе издание, поэтому я немного не готов покупать ее прямо сейчас. Макэльрит предлагает на своем сайте отличную подборку сопутствующих материалов. Оба этих источника будут интересны вам после книги «Байесовская статистика – это здорово». Наконец, порекомендую «Doing Bayesian Data Analysis» под авторством Крушке.
В самом конце года успеваем поделиться с вами новостью о том, что приступаем к работе «Bayesian Statistics the Fun Way» от издательства No Starch Press. Предлагаем перевод развернутого интервью с автором книги; текст касается как самой книги, так и смежных с ней тем, и даже дополнительного чтения.

Я, как и большинство разрабов, интересуюсь сразу множеством вещей: функциональным программированием, операционными системами, системами типов, распределенными системами и наукой о данных. Вот почему я так воодушевился, узнав, что Уилл Курт, автор книги Get Programming with Haskell, написал книгу по байесовской статистике, которая вышла в издательстве No Starch Press. Найдется не так много людей, пишущих книги на разные темы. Я уверен, что Уиллу есть чем поделиться с читателями в своей новой книге – и не разочаровался в ней. Книга – отличный вводный материал, специально для тех, кому не поздоровилось с суровой математикой, но все равно хочется чего-то добиться в области Data Science. Новую книгу Курта я рекомендую читать после Think Stats, но до «Вероятностное программирование на Python: байесовский вывод и алгоритмы», Bayesian Analysis with Python и Doing Bayesian Data Analysis.
1. Зачем нужна еще одна книга по статистике?
Практически все из множества существующих в настоящее время книг по байесовской статистике предполагают, что у читателя уже есть либо общие представления о статистике солидный базис в программировании. Поэтому в настоящее время байесовская статистика часто воспринимается как продвинутая альтернатива для классической (т.е. частотной) статистики. Таким образом, хотя байесовская статистика и пользуется растущей популярностью, материалы по ней рассчитаны в основном на людей, уже имеющих хорошую количественную подготовку.
Когда человек решает попросту «изучить статистику», он берет вводную книгу, в которой статистика излагается с частотной точки зрения, дочитывает ее, наполовину разобравшись в куче тестов и правил и чувствует, что вся эта тема очень запутанная. Я хотел написать такую книгу по байесовской статистике, которую каждый может взять, прочитать и по прочтении получить интуитивное представление о том, каково мыслить статистически и как решать при помощи статистики реальные задачи. Я не вижу никаких причин, почему бы именно байесовская статистика не могла послужить первым вводным курсом в эту тему для абсолютного новичка.
Мне было бы очень приятно, если бы когда-нибудь при слове «статистика» люди стали подразумевать именно байесовскую статистику, а частотная статистика стала просто одной из академических ниш. Для этого нужно больше книг, в которых знакомство со статистикой для широкого круга читателей предлагалось бы именно с использованием байесовских методов, причем, автор учитывал, что это может быть самое первое знакомство читателя со статистикой.
Я сразу подумывал назвать эту книгу «Statistics the Fun Way» («Статистика – это здорово»), но полагал, что, скорее всего, получу ворох гневных писем от людей, купивших такую книгу для подготовки к вступительному экзамену по статистике – и обнаруживших, что речь там совсем про другое! Надеюсь, моя книга станет маленьким шагом к тому времени, когда на вступительных экзаменах станут спрашивать именно байесовскую статистику, и читать такую книгу будет целесообразно даже для тех, кто просто готовится к экзамену.
2. Какова целевая аудитория книги? Может ли читать ее человек без какого-либо математического бэкграунда?
Работая над «Байесовская статистика – это здорово», я стремился создать книгу, в принципе, понятную каждому, кто усвоил математику в объеме программы для старших классов. Даже если вы лишь смутно припоминаете алгебру, темп изложения в книге такой, что вы сможете за ней поспевать. Байесовская статистика требует самую малость математического анализа и тем более упрощается при небольшом сопровождении программным кодом, поэтому я добавил в книгу два приложения, в которых даны основы языка R. Этого материала достаточно, чтобы R послужил вам продвинутым калькулятором, а базовые идеи математического анализа изложены в таком объеме, чтобы вы разобрались со всеми примерами из этой книги, где речь заходит об интегралах. Однако, я обещаю, что для чтения книги не придется решать никаких задач из области математического анализа.
Притом, насколько я потрудился, стараясь максимально сократить тот багаж математических знаний, что нужны для чтения книги, вы, читая ее, постепенно начнете усваивать математический образ мышления. Если вы как следует понимаете математику, которой оперируете, то станете понимать ее еще лучше. Поэтому я не пытался уклоняться от реальной математики, а, скорее, шаг за шагом объясняю ее, так, чтобы вся математика постепенно стала казаться вам очевидной. Как и многие, я когда-то считал, что математика – запутанная наука, и работать с ней сложно. Со временем же я убедился, что при правильном подходе математика не доставляет почти никакого труда. Любая путаница в математике обычно возникает только из-за попыток слишком быстро пройти материал – из-за этого упускаются важные этапы, необходимые для правильного рассуждения.
3. Почему программист должен изучать теорию вероятности и статистику?
Я действительно считаю, что каждый должен в каком-то объеме изучить теорию вероятности и статистику, так как эти знания помогут судить о неопределенности, которая повсюду окружает нас в жизни. Что касается программиста, ему точно придется иметь дело с некоторыми типичными задачами, где полезно понимать статистику. Весьма вероятно, что, в какой-то период профессиональной карьеры вам придется писать код, в котором принимаются некоторые решения на основе априори нечетких факторов. Возможно, это будет измерение конверсии веб-страницы, генерация некой случайной награды в игре, случайное распределение пользователей по группам, либо даже считывание информации с какого-нибудь нечеткого датчика. Во всех этих случаях уверенное понимание теории вероятности вам очень поможет. Моя собственная практика показывает, что вероятностный подход очень помогает в отладке многих багов, которые сложно воспроизвести, либо отследить до сложной проблемы. Если оказывается, что баг обусловлен недостаточной памятью, то можно ли быть уверенным, что баг станет возникать чаще, если память еще сильнее урезать? Если сложный баг можно объяснить двояко, то какую возможность лучше исследовать первой? Во всех подобных случаях может помочь теория вероятности. Разумеется, расцвет машинного обучения и Data Science приводит к тому, что инженерам все чаще приходится иметь дело с такими задачами, где программирование предлагает непосредственную работу с вероятностями.
4. Можно ли вкратце описать разницу между частотным и байесовским подходом к теории вероятности?
В частотной трактовке вероятность интерпретируется как утверждение о том, как часто должно происходить событие при многократных попытках. Так, дважды подбросив монетку, следует ожидать, что она 1 раз выпадет орлом, поскольку у монетки две стороны, и на одной из них орел. В байесовской трактовке вероятность интерпретируется как некоторая характеристика наших знаний, в принципе, как продолжение логики. Вероятность выбросить монетку орлом равна 0,5 поскольку я не вижу причин, по которым орел должен выпадать чаще решки. Итак, в случае подбрасывания монетки оба подхода вполне работоспособны. Однако, когда речь заходит о таких вещах, как шансы вашей любимой команды выиграть кубок мира, фактор степени уверенности становится гораздо весомее. Это, кстати, еще и означает, что байесовская статистика выступает с утверждениями не о мире, а о нашем понимании мира. Поскольку каждый понимает мир немного по-своему, байесовская статистика помогает нам учесть эти различия в нашем анализе. Во многих отношениях байесовский анализ – это наука об эволюции мнений.
5. Почему основное внимание в книге уделено именно байесовскому подходу?
Есть множество по-настоящему веских философских оснований сосредоточиться именно на байесовской статистике, но я руководствовался совершенно практичной причиной: с байесовским подходом все становится логично. Опираясь на относительно небольшой набор интуитивно понятных правил, можно выработать решение практически для любой проблемы, которая может вам попасться. Вот почему байесовская статистика обладает такой силой и гибкостью, и вот почему она так легка в изучении. Думаю, байесовский способ рассуждения отлично подходит именно программистам. Вы не пытаетесь решить задачу при помощи импровизированных тестов, а рассуждаете над ней и постепенно приходите к действительно оправданному решению. В принципе, байесовская статистика – это и есть рассуждение. Вы соглашаетесь со статическим анализом, только если он подлинно логичен и представляется вам убедительным, а не потому, что ваш произвольный с виду тест выдает вам некоторое столь же ничем не подкрепленное значение. Кроме того, байесовская статистика позволяет усомниться в результате и с качественной точки зрения. В повседневной практике часто бывает так, что двум людям представлены одни и те же факты, но выводы у них получаются разные. Байесовская статистика позволяет формально смоделировать такое расхождение во мнениях, так, что мы можем сами проверить, какие факты понадобятся, чтобы мы изменили свою точку зрения. Не приходится верить изложенным на бумаге результатам из-за какого-то p-значения, вы верите им, так как они кажутся вам по-настоящему убедительными.
6. Как байесовская статистика соотносится с машинным обучением
Среди сходств между машинным обучением (в особенности, нейронными сетями) и байесовской статистикой, о которых мне доводилось размышлять – такое: в обеих этих дисциплинах математический анализ может крайне усложняться. В принципе, машинное обучение – это понимание и решение очень нетривиальных производных. Вы получаете функцию, а для нее – функцию потерь, затем (автоматически) вычисляете производную и пытаетесь следовать за ней, пока она не приведет вас к оптимальным параметрам. Многие ехидно отмечают, что обратное распространение – это всего лишь «цепное правило», но практически во всех сложных задачах, связанных с машинным обучением, оно применяется очень успешно.
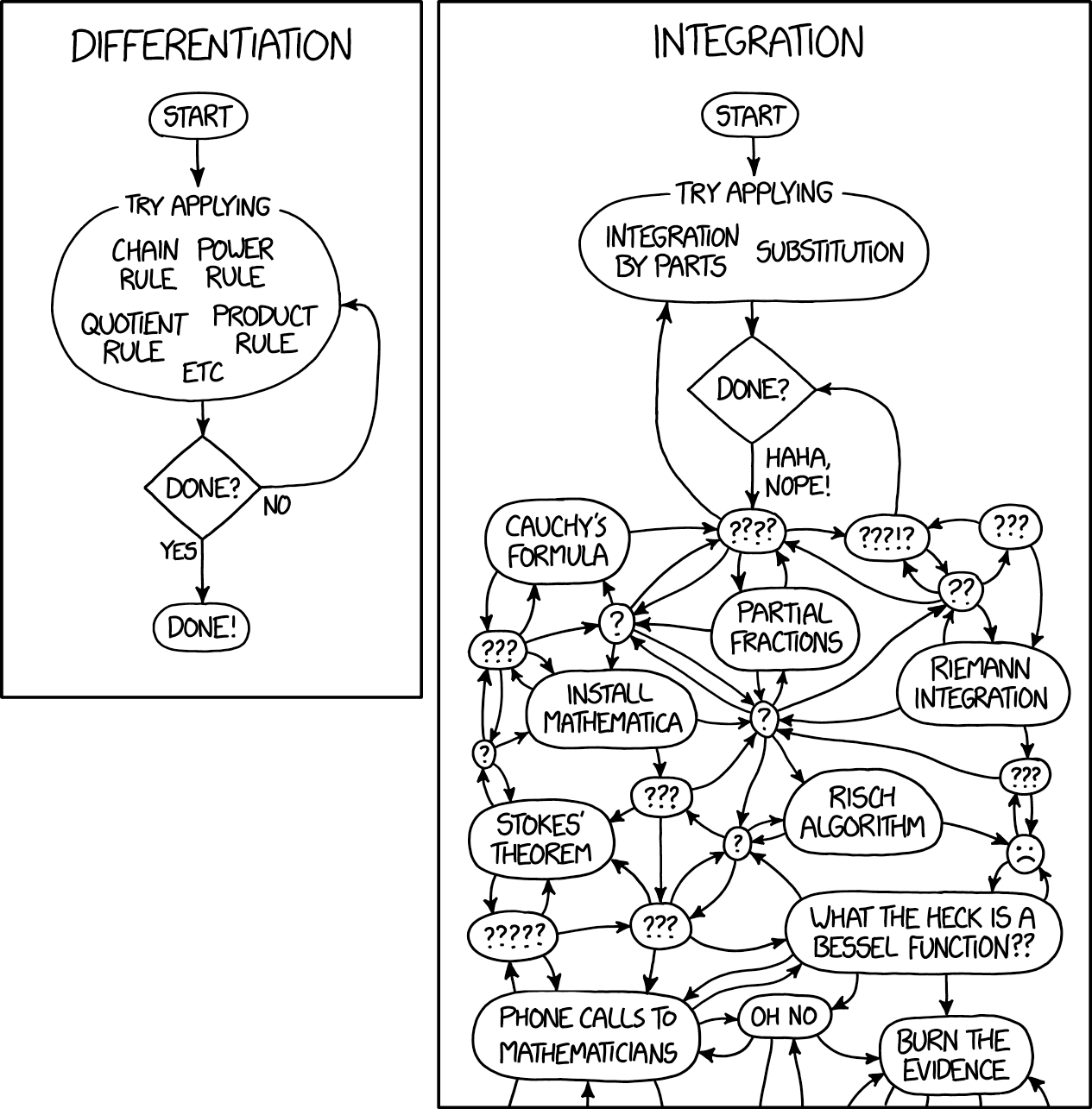
Байесовская статистика – это другая грань математического анализа, связанная с решением по-настоящему сложных интегралов. Майкл Бетанкур, автор Stan, отлично заметил, что практически весь байесовский анализ связан с вычислением ожиданий, то есть, с вычислением интегралов. В результате байесовского анализа у вас остается апостериорное распределение, но как-либо воспользоваться им невозможно, не проинтегрировав его и не получив таким образом конкретный ответ. К счастью, никто не отпускает ехидных комментариев по поводу интегралов, так как все знают, что даже самый тривиальный интеграл довольно сложен. Вот как это афористично сформулировано в одноv из комиксов xkcd:

Вот в таком странном состоянии оказались сегодня машинное обучение и байесовская статистика: простейшие идеи математического анализа мы развиваем до такой степени сложности, какая только поддается вычислениям.
Эта взаимосвязь также подчеркивает один ключевой момент. Когда мы говорим о производных, мы ищем конкретную точку, относящуюся к функции. Так, если известно положение и время, то скорость – это производная, полагающая определить, когда вы двигались быстрее всего. Маленький шаг к прогрессу в МО – это когда вы вычислили единственную метрику лучше, чем кто бы то ни было. Интегрирование – это суммирование всего процесса. Опять же, если вы знаете место и время, то интеграл – это расстояние, он позволяет узнать, как далеко вы продвинулись. Байесовская статистика – это суммирование всего, что вы знаете о проблеме, но она позволяет вам не просто делать отдельные прогнозы, но и охарактеризовать степень уверенности в наших прогнозах, находящихся в широком наборе вариантов. Прогресс в области байесовской статистики – это понимание все более сложных информационных систем.
7. Если читатели захотят глубже познакомиться с темой книги, какие материалы (книги, курсы, блоги) вы им посоветуете?
Максимум вдохновения я почерпнул из книги И. Т. Джейнса “Probability Theory: the Logic of Science”. Втайне надеюсь, что моя книга «Байесовская статистика – это здорово» сможет стать аналогом его книги, но рассчитанным на широкий круг читателей. Работать с книгой Джейнса – задача не из легких, причем, в ней представлен весьма радикальный извод байесовской статистики. Обри Клейтон оказал читателям изрядную услугу, составив серию лекций по главам этой книги.
Разумеется, если вам понравится книга, то, вероятно, вам понравится и мой блог. В последнее время я не так много писал туда, так как писал книгу «Байесовская статистика – это здорово», а до этого «Get Programming with Haskell», но сейчас у меня уже голова ломится от идей, и далеко не все они посвящены строго байесовским темам. Как правило, я размышляю на какую-нибудь тему из области статистики/вероятности, и из этой идеи аккуратно выделываю новую статью для блога.
8. По вашему опыту, какая концепция из области теории вероятности/статистики особенно сложна для понимания?
Честно говоря, самое сложное – это интерпретация вероятностей. Люди в самом деле утратили веру во многих байесовских аналитиков, таких, как Нейт Силвер (и многие другие), когда те прогнозировали, что Хиллари Клинтон с вероятностью 80% выигрывает выборы 2016 года – а она проиграла. Люди сочли, будто их кто-то обманул, и все были неправы, но, на самом деле, вероятность 80% — это не так много. Если врач скажет мне, что мои шансы на выживание – 80%, то я серьезно занервничаю.
Как правило, эта проблема решается так: указываем на вероятности как таковые и заявляем, что они плохо подходят для выражения неопределенности. Чтобы справиться с таким неудобством, приходится использовать коэффициенты или отношения правдоподобия, либо какую-нибудь децибел-подобную систему, например, такую, как джейновская концепция «доказательств» (evidence). Однако, я, как следует поразмышляв о вероятностях достаточно долго, я пришел к выводу, что однозначно годного способа для выражения неопределенности не существует.
Суть проблемы в том, что каждый из нас в глубине души убежден, что в мире есть определенность. Даже опытных специалистов по теории вероятности гложет такое ощущение, что, может быть, если выполнить верный анализ, узнать нужные априорные данные, добавить в вашу иерархическую модель еще один уровень, то все у вас получится, и вы избавитесь от неопределенности или как минимум ее уменьшите. Вероятности отчасти привлекательны мне этим причудливым сочетанием двух этих факторов: стремлением осмыслить мир и признанием того, что, как бы вы ни старались, мир все равно чем-нибудь вас удивит.
9. Что вы думаете о p-значениях как о мере статистической значительности? Могли бы вкратце описать, что такое p-хакинг?
В случае с p-значениями две вещи часто понимаются неверно. Во-первых, разумный человек не будет пытаться отвечать на вопросы при помощи p-значений. Представьте, как выглядел бы следующий разговор на работе:
Менеджер: “Вы пофиксиили этот баг, как вам было поручено?”
Вы: “Ну, я более чем уверен, что не пофиксил его…”
Менеджер: “Если вы его пофиксили – пометьте, что пофиксили.”
Вы: “О, нет, я никак не могу утверждать, что пофиксил его …”
Менеджер: “Вы что же, собираетесь пометить его ‘не буду фиксить’?”
Вы: “Нет, нет, конечно же все совсем не так ”
p-значения многих путают, так как они по природе своей неясные. Байесовская статистика сообщает вам апостериорную вероятность, которая представляет собой положительный ответ на вопрос, сформулированный так, как вы хотите. В вышеприведенном диалоге байесианец говорит: «Я вполне уверен, что баг исправлен». Если менеджер хочет, чтобы вы ответили более уверенно, то байесианец может собрать дополнительную информацию и сказать: «Я, в принципе, уверен, что он исправлен».
Вторая проблема – это укоренившаяся привычка выбирать 0.05 в качестве какого-то волшебного, якобы осмысленного значения. Возвращаясь к предыдущему вопросу о понимании вероятностей, 5%-я вероятность того, что произойдет некоторое событие, еще не означает, что это событие редкое. 5%-я вероятность получить 20 очков будет у вас при броске 20-гранной кости. Однако, любой, кто играл в «Подземелья и драконы», знает, что это далеко не невозможно. За пределами РПГ бросок кости – не лучший инструмент, чтобы отличать истину от лжи.
Здесь мы и подходим к p-хакингу. Вообразите, что вы играете в «Подземелья и Драконы» вместе с друзьями – и вы бросили 20 двадцатигранных костей сразу. Затем вы указываете на ту единственную, на которой выпало 20 очков, и объявляете: «именно эту кость я и собирался бросать, а все остальные были тестовые». Формально вы действительно набрали 20 очков, но ведь это все равно жульничество, согласитесь. В этом и заключается сущность p-хакинга. Вы делаете анализ до тех пор, пока не найдете нечто «существенное», а затем заявляете, что именно это вы и искали с самого начала.
10. Заключительные рекомендации о том, какую книгу лучше прочесть после вашей?
Теперь, когда работа над книгой закончена, я понемногу могу начинать наверстывать время и читать те книги, которые не успел прочесть, пока работал над собственной. Мне очень нравится «Bayesian Analysis with Python» Освальдо Мартина (знаю, недавно он давал интервью Not Monad Tutorial). Это отличная книга, в которой байесовский анализ рассматривается сквозь призму PyMC3. Мир вероятностного программирования в самом деле кажется мне очень увлекательным, и он будет все более и более становиться существенной составляющей практической байесовской статистики. Еще одна книга, которую я очень хочу прочитать — “Statistical Rethinking” Ричарда Макэльрита. Вскоре у нее выходит второе издание, поэтому я немного не готов покупать ее прямо сейчас. Макэльрит предлагает на своем сайте отличную подборку сопутствующих материалов. Оба этих источника будут интересны вам после книги «Байесовская статистика – это здорово». Наконец, порекомендую «Doing Bayesian Data Analysis» под авторством Крушке.


TiesP
Через месяц исполнится год этой статье) Как у вас успехи с переводом? Когда ожидать?
ph_piter Автор
Книга планируется к 19.02.21