1. Введение

Услышав из авторитетных уст, что «автоматы — вещь событийная» [3], понял, что конечные автоматы заклеймили окончательно. Судите сами: в библиотеке Qt реализована событийная модель автоматов [1], в UML — они же [2], смотрим на автоматы пакета расширений Simulink-Stateflow системы MATLAB [4] (далее просто Stateflow) и там о событиях и т.д. и т.д. В таком контексте утверждение д.т.н. А.А. Шалыто трактовать по-другому сложно, т.к. ничего иного уже не может быть, потому что быть не может.

Но, если вспомнить теорию конечных автоматов (ТКА), то в ней о событийных автоматах нет ни слова! Но чтобы противоречить теории нужны веские аргументы. А есть ли основания сомневаться в профессионализме Д. Харелла, как создателя нотации, на которой базирует свои идеи язык UML, пакет Stateflow, которые в свою очередь небезызвестны А.А. Шалыто? Ведь, UML, Stateflow, SWITCH-программирование и иные варианты автоматного программирования существуют и в той или иной мере успешно работают.

Так можно ли снять «клеймо событийности» с модели конечных автоматов, отделив «котлеты от мух»? Т.е. разделить теорию автоматов и вычислительные модели, подобные модели Д.Харела. И считать, что последние, хотя и используют терминологию теории автоматов, представляют, судя по их реализации, развитие модели блок-схем программ.

Замечание 1. Речь в данном случае идет о модели управления программ, а не о самой модели программ (подробнее о моделях см. [5]).

Итак, напомним, библиотека Qt реализует событийную модель конечного автомата, которую заимствовала из UML. Эту же модель реализует Stateflow. Т.е. источник событийности — UML, где автоматы базируются на нотации, предложенной Д. Харелом. Но винить последнего в создании подобного автоматного программирования было бы тоже не верно, т.к. «событийность» — это тенденция современных подходов к реализации программных моделей. В ее основе как авторитетные мнения типа упомянутого «автоматы — вещь событийная», так и высокая популярность языков и технологий типа UML. Без сомнения, это и результат мимикрии автоматов под существующие принципы работы операционных систем.

Но, повторимся, как это не покажется странным, а для кого-то, возможно, даже станет новостью, в теории автоматов нет событийной модели конечного автомата. По крайней мере в той ее части, которая считается классической (см. подробнее, например, [6] или [7]). Налицо явное противоречие между теорией и практикой. В такой ситуации нужно что-то делать с теорией или как-то влиять на практику. Но, может, программисты правы в своем стремлении доработать модель конечного автомата, включив в нее понятие «событие» [8, 9]?

Но как связать желания программистов с тем, что «наибольшие трудности при использовании автоматного подхода связаны с пониманием особенностей функционирования автоматов в событийных системах» (см. [8]). Хотелось бы разобраться в причинах подобных проблем и в этом контексте реализовать событийные автоматы и/или их аналог. В этих целях для конкретики возьмем реализацию автоматов в Qt и повторим их, используя модель классического конечного автомата.

Подобная реализация событийных автоматов необходима в целях оценки и/или преодоления упомянутых «особенностей». Использование классической модели распространит теорию автоматов также на практику «событийного программирования». И, в конце концов, аналог на базе другой модели только расширит область приложения моделей конечных автоматов.

2. События, сигналы и гендерная идентичность автоматов

В UML событие (event) — «это значимое явление, которое имеет определенное положение во времени и пространстве… и влечет за собой определенные последствия» [10]. Событие в теории автоматов – это подмножество входных символов, представимых символами выходного алфавита (есть в ТКА даже понятие алгебры событий) [6]. То же, что вызывает переход автомата, в теории автоматов называется входными сигналами. Они — последствия и «причина, перехода автомата из одного состояния в другое. При этом выходные сигналы — »реакция автомата на входные сигналы". И те и другие «относятся к моментам времени, определяемым соответствующими переходами авто-мата» [6]. В UML же сигнал (signal) — «это именованная сущность, служащая средством коммуникации между объектами» [10].

Таким образом, названия терминов одинаковы, но смысл, вкладываемый в них раз-ный. Хотя, если переставить их местами, то можно обнаружить сходство: становится понятно, что событиям в UML соответствуют сигналы конечных автоматов в ТКА. Но, может, и под термином «конечный автомат» скрываются разные сущности? Попробуем разобраться и с этим, начав с событий…

Событийный автомат является пассивным автоматом, т.к. функционирует только в моменты прихода событий. В противоположность ему классический автомат представляет активную модель. Он функционирует вне привязки к чему бы то ни было (подробнее о пассивных и активных автоматах см. [9]). Здесь напрашивается ассоциация с двумя бегунам, где первого подгоняют пинками (событиями), а второй бежит сам.

В отличие от [8] мы не будем поначалу связывать моменты возникновения событий с запуском автомата. Так мы останемся в рамках теории автоматов, которая определяет асинхронный характер функционирования автоматов по отношению к внешней среде. В ней говорится лишь о дискретном времени, в котором смена состояний осуществляется за сколь угодно малый, но не равный нулю, промежуток реального времени. А причина переходов — текущее состояние и входные сигналы автомата, где последствия — установка нового состояния и значения выходных сигналов автомата (подробнее об определении автоматов см. [6]).

Теория автоматов гибка в определении дискретного времени, являющегося моде-лью реального времени. Так, такт дискретного времени может иметь фиксированную или плавающую величину отрезка реального времени, а автоматы в соответствии с этим называться синхронными или асинхронными. При этом сопоставленный такту отрезок времени может иметь любое, в том числе и бесконечно малое, но не равное нулю, значение.

Замечание 2. Модель конечного автомата одна из немногих формальных моделей, которая включает в свое определение модель реального времени в явной форме.

В результате формально «бесконечное» быстродействие активного автомата позволяет любое событие трактовать как потенциальный входной сигнал (в терминах UML ему соответствует условие[11]). Автомату нужно будет только «ловить» подобные со-бытия/сигналы и паузы между ними. Все это фактически определяет протокол совместной работы среды и автомата. Протокол должен решать и проблему распознавания последовательно поступивших одинаковых событий. Без этого, например, два одинаковых символа, поступившие один за одним, могут быть восприняты как один.

Формально нюансы обработки событий не существенны (см. те же абстрактные автоматы), но при практической реализации алгоритмов, построенных по типу событийной модели, их необходимо учитывать. В случае библиотеки Qt их учет сокрыт в классах реализации автомата. Далее мы займемся учетом отличий событийных и классических автоматов на примере реализации простейшего калькулятора из [1], где приведена его «событийная реализация». В противовес этому решению будут созданы эквивалентные модели на основе классического конечного автомата.

3. Модели калькулятора

Итак, приступим… Называем события сигналами, обычные автоматы событийными… или в обратном порядке и/или наоборот? Тьфу! Запутался. Короче, полная «глокая куздра штеко будланула» и что-там «кудрячит». Чтобы разобраться «who is who», что и как называть, самый верный путь это выбрать конкретного «бокра» и его и «будлануть»… Таким «бокром» далее будет программа «автоматного калькулятора».

3.1. Активная модель калькулятора

На рис. 1 приведена исходная модель класса Calculator из [1]. По внешнему виду она похожа на классический абстрактный автомат без выхода. Отличие в том, что Qt подключает действия при входе в состояние и при выходе из него. На выходе они за-пускаются сигналом exited(), а при входе в состояние – сигналом entered(). Но, отметим, на графе эти действия никак не представлены.

Если сравнить модель на рис. 1 с автоматом с абстрактным состоянием (другие его названия – структурный, логический автомат), можно легко видеть, что действиям на выходе из состояния соответствуют сигналы автомата Мили, а действиям на входе в него – сигналы автомата Мура.
Замечание 3. Далее, рассматривая программную реализацию модели, мы будем го-ворить не о сигналах, событиях, условиях и т.п., а о действиях автоматов, считая, что на уровне программы они ассоциируются с определенными программными действиями, которые в общем случае представлены программными функциями.

Так называемый совмещенный автомат Мили-Мура (или по-другому смешанный автомат [12]), эквивалентный автомату на рис. 1, приведен на рис.2, где справа от графа показаны также функции, соответствующие входным и выходным сигналам автомата.


Рис.1. Диаграмма событийного автомата класса Calculator


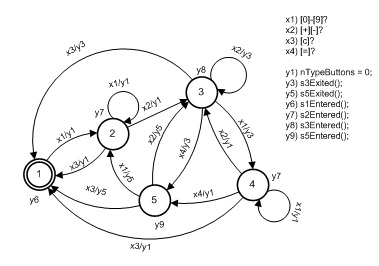
Рис.2. Граф автомата Мили-Мура класса Calculator

Для модели, подобной автомату на рис.2, под входными/выходными действиями будем понимать предикаты и действия, представляющие собой программные функции-методы [автоматных] классов. Предикаты анализируют текущее состояние элементов памяти (переменных, свойств класса), никак (это важно!), на них не влияя, но в зависимости от их значения возвращающие булевское значение. Действия значения не возвращают, но изменяют элементы памяти.
Из рис. 2 следует, что у модели калькулятора, как у «черного ящика», имеется по числу предикатов и действий четыре входных канала и семь выходных каналов. Легко видеть, что по сравнению с абстрактным автоматом, имеющим по определению не более одного входного и одного выходного канала, структурный автомат, имеющий множество каналов, более универсален, гибок и удобен.

Модель на рис. 2 можно упростить, «склеив» состояния 1 и 2. Для этого сначала нужно превратить исходный автомат в автомат Мили. Его получаем, нагружая входящие в состояния дуги сигналами, представленными сигналами вершин автомата Мура. После этого операция склеивания становится очевидной. Результат склеивания состояний в состояние 2, которое теперь становится инициальным, представлен на рис. 3.


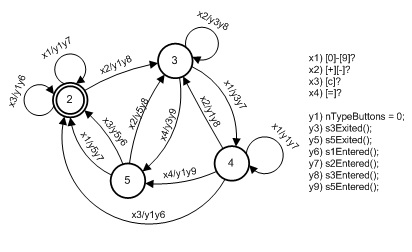
Рис.3. Результат преобразования и склеивания состояний автомата на рис.2

Поясним действие y1 и переменную nTypeButtons. В сумме они реализуют протокол, моделирующий события. Переменная nTypeButtons своим значением определяет тип входных символов автомата, разделяя их на цифровые символы, символы операций, символ «сброс» и символ «равно». Ее значение, равное нулю, означает отсутствие входных символов (не нажата ни одна из клавиш калькулятора). После обработки символа это же означает, что входной символ воспринят автоматом. Так блокируется повторная реакция на входной символ.

Код класса калькулятора, созданного в рамках среды автоматного визуально-компонентного программирования (ВКПа) [5], демонстрируют листинги 1, 2.


Поясним. В ВКПа любой автоматный класс наследует свойства базового автоматного класса LFsaAppl. Метод Create() создает копии классов, включенных в динамические библиотеки автоматных процессов. Виртуальный метод MooreAction() перекрывается в случае выбора модели автомата Мура, определяя действия, сопоставленные состояниям автомата. Методы x[n] и y[n] — это предикаты и действия, сопоставленные входным/выходным каналам автомата. Алгоритм поведения [автоматного] класса представлен таблицей переходов (см. листинг 2), состоящей из массива строк типа LArc. Остальной код повторяет код исходного класса Calculator.


Обратите внимание, листинг 2 содержит три таблицы переходов (две закомментированы). Так реализуются возможности выделенного управления, когда, сняв комментарий, поведение класса можно изменить «по щелчку», не затрагивая его методов и свойств. Метод y10 и соответствующая строка таблица переходов (см. строку, помеченную комментарием SWICH) введены для моделирования SWITCH-технологии (о ней см. подробнее [9]) в рамках технологии ВКПа. В этом случае поведение любого автомата моделируется циклическим вызовом оператора SWITCH, имитирующего поведение автомата (здесь в качестве внешней среды выступает автомат ВКПа).

3.2. Пассивная модель калькулятора

Активная модель калькулятора постоянно сканирует входные каналы. Как только значение переменной nTypeButtons становится отличным от нуля, это служит признаком поступления на вход автомата очередного символа. В результате срабатывает переход и действие y1, обнуляя переменную nTypeButtons, блокирует повторное срабатывание автомата на один и тот же символ.
В отличие от модели «активного калькулятора», событийный автомат не может по определению повторно обработать входной символ. Теперь понятно, что «наибольшие трудности при использовании автоматного подхода… в событийных системах», сводятся, похоже, к подавлению активности активного автомата и привязке его функционирования к событиям. Покажем процедуру перехода к пассивному автомату на примере только что созданного «активного калькулятора».
Среда ВКПа содержит пошаговый режим работы, введенный для отладки автоматных процессов. Но его вполне можно использовать для моделирования событийных автоматов. Для этого нужно 1) задать автоматному пространству, в которое помещен автомат, пошаговый режим работы (заметим, не отдельному автомату, а всему автоматному пространству, содержащему автоматы) и 2) связать моменты появления событий с выполнением одного дискретного шага работы пространства. Как это сделать демонстрирует листинг 3, отражающий только изменения, внесенные в модель (заголовок класса остался неизменным).


Здесь, во-первых, введено дополнительно [начальное] состояние, в котором проверяются ссылка на пространство, где находится автомат, и ссылка на объект, определяющий свойства пространства (в том числе режим его работы). Эх формирует действие y12. Когда ссылки установлены, происходит переход в [бывшее] начальное состояние модели калькулятора с установкой пошагового режима работы автоматного пространства.

Далее модель функционирует в пошаговом режиме работы пространства. Запуск одного шага реализует код, вставленный в обработчики событий, связанных с вводом очередного символа (см. на листинге 3 изменения, внесенные в методы digitButtonPressed и operationButtonPressed).

4. А зачем?

Зачем что-то изобретать, если есть, как можно полагать, более продвинутая событийная модель Д.Харела. Да и как думать по-другому, если ее обкатали в UML, Stateflow, в библиотеке Qt и т.д. и т.п. и не видно особой паники по поводу ее недостатков. Ну, назвали сигналы событиями, а активный автомат превратили в пассивный… А если модель, как утверждают, еще и формально эквивалентна классическим автоматам Мили/Мура, то как в нее не верить? Так-то оно так, если все эти утверждения принимать только на веру…

Возьмем для начала события (именно так мы и поступили выше). У классического структурного автомата имеется, например, множество входных каналов, каждому из которых сопоставлен сигнал, и обрабатываться они могут одновременно/параллельно. Но UML говорится, что «каждый объект может обрабатывать за раз только одно событие»и даже «если два события происходят одновременно, объект все равно будет обрабатывать их по одному» [10]. Таким образом, на уровне определения сигналы и события эквивалентны, но идиллия рушится в процессе реализации переходов модели.

Рассмотрим пример, с которого я начинаю тестировать/изучать любой язык или технологию. Речь о программной реализации модели элемента И-НЕ. Ему на структурном уровне соответствует «черный ящик», имеющий два входных канала и один выходной, а на алгоритмическом — автомат, показанный на рис. 4.


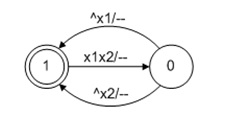
Рис. 4. Автоматная модель элемента И-НЕ

Как создать обычную процедурную модель (см. листинг 4) или как реализовать автомат в ВКПа (см. листинг 5) понятно, но как это же повторить на базе событийного автомата библиотеки Qt не очень ясно из-за проблемы реализации перехода из состояния «1» в состояние «0», требующего одновременного анализа нескольких событий.

Листинг 4. Объектная реализация процедурной модели И-НЕ



Таким образом, пусть реализация событийной модели элемента И-НЕ в рамках автоматных классов Qt будет «домашним заданием» для хабровчан. Я могу только в качестве «вишенки на торте» привести ее решение в рамках Stateflow. Оно приведено на рис. 5. Здесь задействовано послабление Stateflow, разрешающее не помечать переход событием: если имя события не указано, то переход произойдет при наступлении любого события (см. пример метки перехода в [13]).


Рис. 5. Автоматная модель элемента И-НЕ в Stateflow

Таким образом, автоматы в Stateflow представляют собой гибридную (активно-пассивную) модель автомата. Правда, не совсем ясно, как будет вести себя автомат при отсутствии каких-либо событий вообще. Можно предположить, что «замрет» в ожидании событий. А если их не будет? Т.е. в конечном итоге это все же скорее пассивная, чем активная модель автомата. Хотя только по внешнему виду ее сложно отличить от последней.

5. Заключение

Применительно к событиям можно сказать, что в силу активности реализация классической модели автоматов выглядит предпочтительнее модели синхронных автоматов. Если же говорить об автоматном программировании в целом, то пакет расширений Stateflow демонстрирует, каким может быть качественно иное программирование. Но, к сожалению, пока лишь в перспективе, т.к. остаются проблемы из-за вычислительной модели Stateflow, которая по сути остается все еще блок-схемной. Похоже, именно в силу этих причин наряду с автоматами визуальное программирование в Statefow представлено и нотацией блок-схем.

Разобраться, где настоящее автоматное программирование, а где его имитация, одна из основных наших целей. В предыдущей статье [5] мы решили одну из базовых поставленных задач — сформулировали понятие автоматных программ. Далее нужно заняться определением модели управления программ, которая должна быть конечно-автоматной и быть эффективной и удобной для программистов.

Разобравшись с событиями, мы положили начало такой работе. В дальнейших статьях мы будем разбираться уже в деталях модели, предложенной Д.Харелом. Забегая несколько вперед скажем, что она, если уж говорить прямо, исказила понимание автоматов. Но, с другой стороны, и здесь надо отдать ей должное, она выявила проблемы, которые не позволили, не имея ее, в рамках классической модели сформировать эффективное автоматное программирование, которое привлекло бы программистов.

Выше мы выяснили, что, как минимум, на уровне событий проблем у классических автоматов нет. Будем разбираться дальше… Пока же это только начало. Нас ждет еще много интересного и, заметим, не выходя за рамки классической теории автоматов. Это архиважно, если мы хотим иметь действительно автоматное программирование. Пожелаем себе успехов! :)

Список литературы

1. Боровский А.Н. Qt4.7. Практическое программирование на С++. – СПб.: БХВ-Петербург, 2012. – 496 с.
2. БУЧ Г., РАМБО ДЖ., ЯКОБСОН И. Язык UML. Руководство пользователя. Второе издание. Акаде-мия АЙТИ: Москва, 2007. – 493 с.
3. Шалыто А. А. Новая лекция по автоматному программированию. 2019, [Электронный ресурс], Ре-жим доступа: www.youtube.com/watch?v=PPWTxceMutk&feature=youtu.be, свободный. Яз. рус. (дата обращения 5.12.2019).
4. Stateflow. www.mathworks.com/products/stateflow.html, свободный. Яз. англ. (дата обращения 7.01.2020).
5. Машина Тьюринга, как модель автоматных программ. habr.com/ru/post/481998, свободный. Яз. рус. (дата обращения 7.01.2020).
6. Мелихов А.Н. Ориентированные графы и конечные автоматы. – М.: Наука, 1971. – 416 с.
7. КУДРЯВЦЕВ В.Б., АЛЕШИН С.В., ПОДКОЛЗИН А.С. Введение в теорию автоматов – М.: Наука. Гл. ред. физ.-мат. лит., 1985. – 320 с.
8. Туккель Н.И., Шалыто А.А. Реализация автоматов при программировании событийных систем. «Программист», 2002. №4. C.74-80.
9. Поликарпова Н., А. Шалыто А. Автоматное программирование. 2-е изд., – СПб.: Питер, 2011. – 176 с.
10. Рамбо Дж., Якобсон А., Буч Г. UML: специальный справочник. – СПб.: Питер, 2002. – 656 с.
11. Гома Х. UML. Проектирование систем реального времени, параллельных и распределенных прило-жений: Пер. с англ. – М.: ДМК Пресс, 2002. – 2002. — 704 с.
12. ШАЛЫТО А.А. SWITCH-технология. Алгоритмизация и программирование задач логического управления. СПб.: Наука, 1998. 628 с.
13. Рогачев Г.Н. Нотации Stateflow. bourabai.kz/cm/stateflow13.htm, свободный. Яз. рус. (дата об-ращения 10.01.2020).