Сегодня мы отправимся в красочное путешествие по миру клеточных автоматов, попутно изучая некоторые хитрые приемы их реализации, а также попытаемся понять, что скрывается за этой красотой — любопытная игра для праздного ума или глубокая философская концепция, находящая отклики во многих моделях.
Для практики и лучшего понимания следует попытаться самому реализовать приведенные ниже алгоритмы. Ну а если лень, или просто из интереса, можно поиграться с различными имплементациями:
- Golly — небольшая программка использующая оптимальнейшие методы для моделирования клеточных автоматов с различными правилами и сетками. В комплекте есть база шаблонов и предустановок.
- Lenia — набор инструментов для изучения непрерывного варианта "жизни".
- Онлайн симулятор для муравья Лэнгтона. Особо примечательна возможность выбора триангулярной сетки, в которой стандартные правила ведут себя как генератор пиксельных космических кораблей

Одномерный случай
Одномерный клеточный автомат представляет с собой отрезок разбитый на равные части — ячейки. Каждая ячейка может принимать одно из двух состояний, условно 0 или 1, черный или белый, живой или мертвый и т. д. Состояние каждой ячейки меняется по определенному правилу, учитывающему состояние соседей. Если принимать во внимание только ближайших соседей, то мы получим комбинацию из восьми состояний искомой ячейки и пары соседей. Каждой из этих комбинаций можно поставить в соответствие одно новое состояние для искомой ячейки, из чего следует общее количество правил равное 256 (количество 8-битных слов).
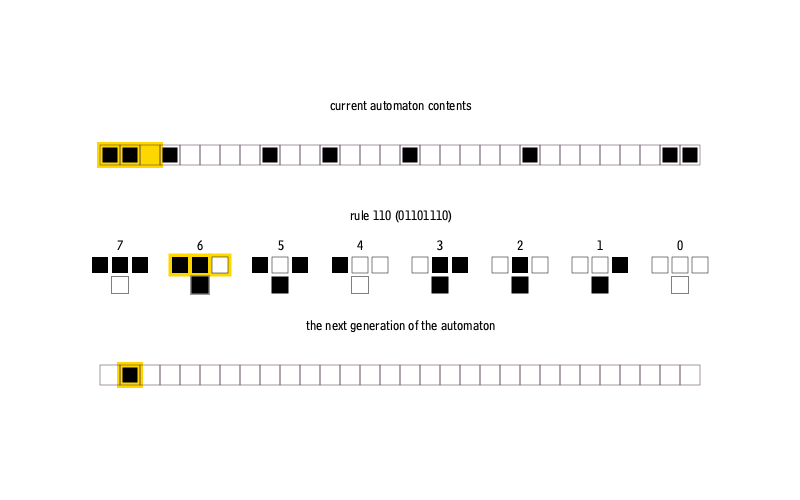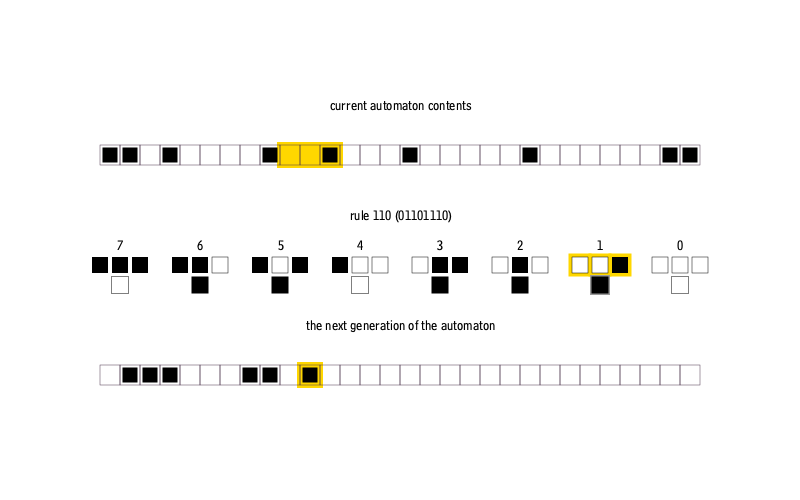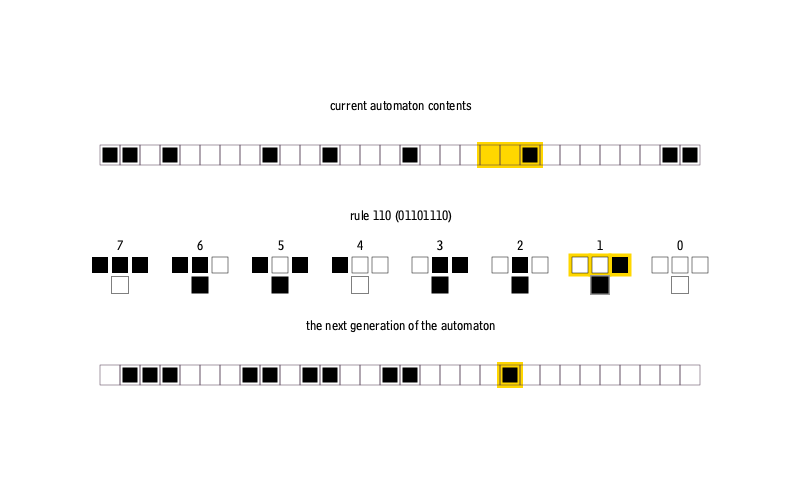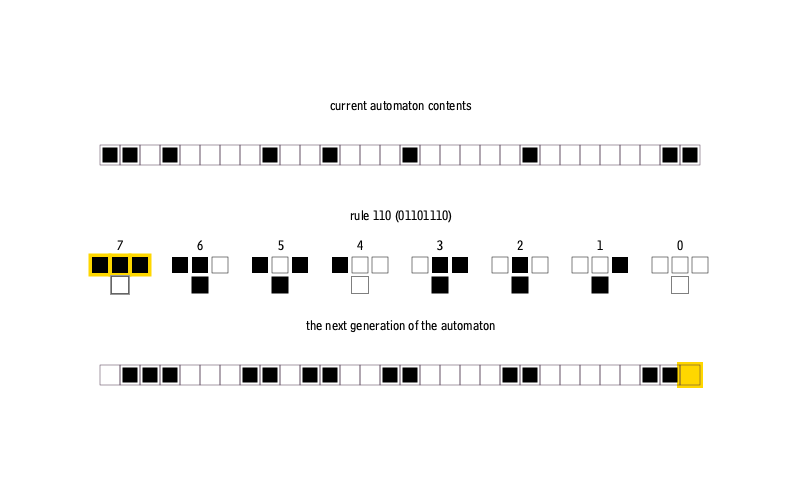
Чтобы надежно закрепить образ в своей нейросети, реализуем функцию визуализирующую одномерные клеточные автоматы.
Для начала следует установить и подгрузить все необходимые пакеты:
using Pkg
pkgs = ["Images", "ColorSchemes", "FFTW"]
for p in pkgs
Pkg.add(p)
end
using Images, ColorSchemes, FFTW, LinearAlgebra: kron
using Random: bitrand
cd("C:\\Users\\User\\Desktop\\Mycop")Правила для одномерных клеточных автоматов выражают числами от 0 до 255 (десятичные представления восьмибитных слов). Значит наша функция должна уметь представлять номер правила в двоичном виде, и составлять для него паттерн. Затем, при наивной реализации, происходит проход по всем ячейкам с заменой состояний:
# размеры, правило, множитель для масштаба картинки
function cellauto( n::Int64, m::Int64, rule::Int64, s::Int64 = 1 )
ptrn = digits(Bool, rule, base = 2, pad = 8)
bt = [ bitstring(i)[end-2:end] for i = 0:7 ]
d = Dict( bt[i] => ptrn[i] for i = 1:8 ) # словарь
M = falses(n,m)
M[1,m ? 2] = true
#M[1,:] .= bitrand(m)
for i = 1:n-1, j = 2:m-1
key = "$(M[i, j-1]*1)$(M[i, j]*1)$(M[i, j+1]*1)"
M[i+1,j] = d[key]
end
kron(M, ones(Int,s,s) ) # произведение Кронекера
end
M0 = cellauto(100, 200, 30, 4)
Gray.( M0 )
Это правило 30, одно из любимых Стивена Вольфрама. Он, кстати, назначил денежные призы за решения задач связанных с этим правилом. Действительно, в этом что-то есть: периодичность граничащая с хаосом, плюс спонтанное зарождение упорядоченных структур… Но лично меня зацепили треугольники Серпинского, которые часто встречаются здесь и там. А для одномерных КА они довольно частое явление:
Arr = cellauto.(40, 40, [0:23;], 2);
Imgs = [ Gray.(a) for a in Arr ]
reshape(Imgs, 4,6)
В кругах и в цвете
Приверженцам объектно ориентированного программирования можно предложить вариант, где клеточный автомат выполнен в виде структуры. В этом случае будет удобно реализовать варьирование цвета и даже круглые поля:
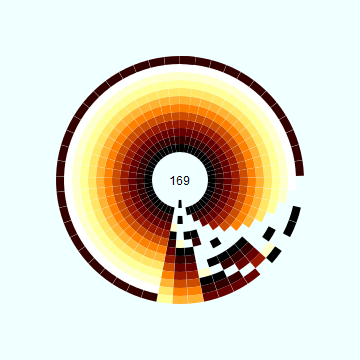

Визуализация выполнена с помощью пакета Luxor, который мы разбирали ранее.
Игра в жизнь
"Жизнь" Конвея — самый популярный из двумерных (да и трехмерных) клеточных автоматов. Эта модель отдаленно напоминает копошение бактерий в чашке Петри, и обладая Тьюринг полнотой, может послужить основой для чего угодно: моделирования мышления, компьютеров (архитектуры тетриса) и самой себя.
Множество энтузиастов находят все новые структуры: осцилляторы, глайдеры, корабли (на гусеничном ходу!) и фабрики. То есть, вся прелесть здесь заключается в том, что на основе простых правил можно создавать сложные структуры, откуда возникает соблазн попытаться распространить данную модель на фундаментальные законы Естества. В частности С. Вольфрам балует нас подобными высказываниями. Вопрос, на сколько это правдоподобно и, главное, полезно, всегда вызывает споры, так что, не будем на нем заостряться. Лучше реализуем "Жизнь" использующую преобразования Фурье.
Жизнь без Фурье и не жизнь вовсе
Тем, кто занимался обработкой изображений, работа с БПФ в таком аспекте должна быть знакома. Остальным можно посоветовать попробовать заняться обработкой изображений, так как это очень интересно, и снабдит вас полезными абстракциями для понимания линейной алгебры.
За основу использовался алгоритм из хабровской статьи
function makefilter(N::Int64)
filter = zeros(Complex, N, N);
IDX(x, y) = ( (x + N) % N ) + ( (y+N) % N ) * N + 1
filter[IDX(-1, -1)] = 1. ;
filter[IDX( 0, -1)] = 1. ;
filter[IDX( 1, -1)] = 1. ;
filter[IDX(-1, 0)] = 1. ;
filter[IDX( 1, 0)] = 1. ;
filter[IDX(-1, 1)] = 1. ;
filter[IDX( 0, 1)] = 1. ;
filter[IDX( 1, 1)] = 1. ;
return fft( real.(filter) )
end
function fftlife(N = 16, steps = 100, dx = 0, glider = true)
if glider
state = falses(N, N)
state[4,5] = state[5,6] = state[6,6] = true
state[6,5] = state[6,4] = true
else
state = bitrand(N, N)
end
filter = makefilter(N)
for i in 1:steps
tmp = fft( real.(state) ) # forward
tmp .*= filter
summ = ifft(tmp) # reverse
for i in eachindex(state)
t = round( Int, real(summ[i]) ) >> dx
state[i] = ( state[i] ? t == 2 || t == 3 : t == 3 )
end
save("KonLife_$(N)x$(N)_$i.png", kron( Gray.(state), ones(8,8) ) )
end
end
fftlife(16, 60)
Приятные бонусы этого подхода — это сравнительно быстрая отработка БПФ в силу его отполированности, и закольцованность граничных условий (действо происходит как бы на поверхности тора). Собственно, теперь можно обобщить "жизнь" непрерывным случаем.
Гладкая жизнь
Вот так в общем виде выглядит модель:
Состояние теперь описывается не 1 и 0, а сигмоидой, соседи учитываются в некотором радиусе, а еще понадобится решать дифуры.
function clamp(x)
y = copy(x)
y[x.>1] .= 1
y[x.<0] .= 0
y
end
function func_linear(X, a, b)
Y = [ (x-a + 0.5b)/b for x in X ]
Y[X.<a-0.5b] .= 0
Y[X.>a+0.5b] .= 1
return Y
end
function splat!(aa, ny, nx, ra)
x = round(Int, rand()*nx ) + 1
y = round(Int, rand()*ny ) + 1
c = rand() > 0.5
for dx = -ra:ra, dy = -ra:ra
ix = x+dx
iy = y+dy
if ix>=1 && ix<=nx && iy>=1 && iy<=ny
aa[iy,ix] = c
end
end
end
function initaa(ny, nx, ra)
aa = zeros(ny, nx)
for t in 0:((nx/ra)*(ny/ra))
splat!(aa, ny, nx, ra);
end
aa
endfunc_smooth(x::Float64, a, b) = 1 / ( 1 + exp(-4(x-a)/b) )
sigmoid_a(x, a, ea) = func_smooth(x, a, ea)
sigmoid_b(x, b, eb) = 1 - sigmoid_a(x, b, eb)
sigmoid_ab(x, a, b, ea, eb) = sigmoid_a(x, a, ea) * sigmoid_b(x, b, eb)
sigmoid_mix(x, y, m, em) = x - x * func_smooth(m, 0.5, em) + y * func_smooth(m, 0.5, em)
function snm(N, M, en, em, b1, b2, d1, d2)
[ sigmoid_mix( sigmoid_ab(N[i,j], b1, b2, en, en),
sigmoid_ab(N[i,j], d1, d2, en, en), M[i,j], em )
for i = 1:size(N, 1), j = 1:size(N, 2) ]
endfunction smoothlife(NX = 128, NY = 128, tfin = 10, scheme = 1)
function derivative(aa)
aaf = fft(aa)
nf = aaf .* krf
mf = aaf .* kdf
n = real.(ifft(nf)) / kflr # irfft
m = real.(ifft(mf)) / kfld
2snm(n, m, alphan, alpham, b1, b2, d1, d2) .- 1
end
ra = 10
ri = ra/3
b = 1
b1 = 0.257
b2 = 0.336
d1 = 0.365
d2 = 0.551
alphan = 0.028
alpham = 0.147
kd = zeros(NY,NX)
kr = zeros(NY,NX)
aa = zeros(NY,NX)
x = [ j - 1 - NX/2 for i=1:NY, j=1:NX ]
y = [ i - 1 - NY/2 for i=1:NY, j=1:NX ]
r = sqrt.(x.^2 + y.^2)
kd = 1 .- func_linear(r, ri, b) # ones(NY, NX)
kr = func_linear(r, ri, b) .* ( 1 .- func_linear(r, ra, b) )
#aa = snm (ix/NX, iy/NY, alphan, alpham, b1, b2, d1, d2);
kflr = sum(kr)
kfld = sum(kd)
krf = fft(fftshift(kr))
kdf = fft(fftshift(kd))
#for td in 2 .^(10:-1:3)
for td = 64
aa = initaa(NY,NX,ra)
dt = 1/td;
l = 0
nx = 0
for t = 0:dt:tfin
# 1=euler 2=improved euler 3=adams bashforth 3 4=runge kutta 4
if scheme==1
aa += dt*derivative(aa)
elseif scheme==2
da = derivative(aa);
aa1 = clamp(aa + dt*da)
for h = 0:20
alt = aa1
aa1 = clamp(aa + dt*(da + derivative(aa1))/2)
if maximum(abs.(alt-aa1))<1e-8
break
end
end
aa = copy(aa1)
elseif scheme==3
n0 = 1+mod(l,3)
n1 = 1+mod(l-1,3)
n2 = 1+mod(l-2,3)
f = zeros(NY, NX, 3) # ?
f[:,:,n0] = derivative(aa)
if l==0
aa += dt*f[:,:,n0]
elseif l==1
aa += dt*(3*f[:,:,n0] - f[:,:,n1])/2
elseif l>=2
aa += dt*(23*f[:,:,n0] - 16*f[:,:,n1] + 5*f[:,:,n2])/12
end
elseif scheme==4
k1 = derivative(aa)
k2 = derivative(clamp(aa + dt/2*k1))
k3 = derivative(clamp(aa + dt/2*k2))
k4 = derivative(clamp(aa + dt*k3))
aa += dt*(k1 + 2*k2 + 2*k3 + k4)/6
end
aa = clamp(aa)
if t >= nx
save("$(scheme)\\$(td)_$t.png", Gray.(kron(aa, ones(2, 2) ) ) )
nx += 1;
end
l += 1;
end
end # for td
end
@time smoothlife(256, 256, 20, 3)
В модели много свободных параметров, а также можно поиграться с разными методами для дифуров. В общем, есть простор для исследований. Также анимации всегда можно украсить шейдерами.

Тьюрмиты
Еще один интересный вид машин Тьюринга это тьюрмиты — клеточные автоматы, состояние которых определяется неким агентом, который будет перемещаться по полю в зависимости от этих самых состояний. Наиболее известный представитель этого вида — муравей Лэнгтона.

На клеточное поле, каждая ячейка которого может быть либо черной либо белой, сажается мураш, который будет действовать по следующему алгоритму:
- На чёрном квадрате — повернуть на влево, изменить цвет квадрата на белый, сделать шаг вперед на следующую клетку.
- На белом квадрате — повернуть на вправо, изменить цвет квадрата на чёрный, сделать шаг вперед на следующую клетку.
На rosetta code есть довольно хитрая реализация, где направление муравья задается комплексным числом:
function ant(width, height)
y, x = fld(height, 2), fld(width, 2)
M = trues(height, width)
dir = im
for i in 0:1000000
x in 1:width && y in 1:height || break
dir *= M[y, x] ? im : -im
M[y, x] = !M[y, x]
x, y = reim(x + im * y + dir)
i%100==0 && save("LR//zLR_$i.png", Gray.( kron(M,ones(4,4) ) ) )
end
Gray.(M)
end
ant(100, 100)
Поначалу, поведение агента кажется хаотичным. Но потом появляется магистраль — система выходит на стационар. Прекраснейший пример рождения порядка из кажимого хаоса!
Но самый смак начинается если расширить состояние ячейки за пределы одного бита:
function ant(width, height, comnds;
steps = 10, cxema = reverse(ColorSchemes.hot),
savevery = 100, pixfactor = 20)
ma3x2pix() = [ clrs[k%n+1] for k in M ]
bigpix() = kron( ma3x2pix(), ones(Int64,m,m) )
save2pix(i) = save("$(comnds)_$i.png", bigpix() )
m = pixfactor
n = length(comnds)
colorsinscheme = length(cxema)
M = zeros(Int64, height, width)
y, x = fld(height, 2), fld(width, 2)
st = colorsinscheme ? n
clrs = [ cxema.colors[i] for i in 1:st:colorsinscheme ]
dir = im
for i in 0:steps
x in 1:width && y in 1:height || (save2pix(i); break)
j = M[y, x] % n + 1
dir *= comnds[j] == 'L' ? -im : im
M[y, x] += 1
x, y = reim(x + im * y + dir)
i % savevery==0 && save2pix(i)
end
ma3x2pix()
end
@time ant(16, 16, "LLRR", steps = 100, savevery = 1, pixfactor = 20)
Послойными наращиваниями получаем симметричную структуру, похожую на мозг! Для некоторых цветовых схем получается довольно футуристично

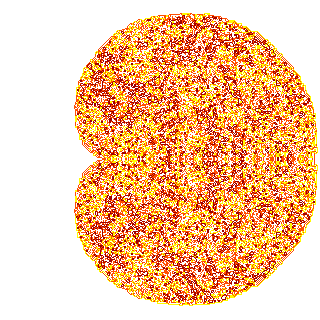
Правда потом он вырождается в жопу кардиоиду. Кстати, ничего еще не напоминает? А если добавить фрактальных наростов?..
# http://rosettacode.org/wiki/Mandelbrot_set
function hsv2rgb(h, s, v)
c = v * s
x = c * (1 - abs(((h/60) % 2) - 1) )
m = v - c
r,g,b =
if h < 60
(c, x, 0)
elseif h < 120
(x, c, 0)
elseif h < 180
(0, c, x)
elseif h < 240
(0, x, c)
elseif h < 300
(x, 0, c)
else
(c, 0, x)
end
(r + m), (b + m), (g + m)
end
function mandelbrot()
w, h = 1000, 1000
zoom = 1.0
moveX = 0
moveY = 0
img = Array{RGB{Float64}, 2}(undef,h, w)
maxIter = 30
for x in 1:w
for y in 1:h
i = maxIter
c = Complex(
(2*x - w) / (w * zoom) + moveX,
(2*y - h) / (h * zoom) + moveY
)
z = c
while abs(z) < 2 && (i -= 1) > 0
z = z^2 + c
end
r,g,b = hsv2rgb(i / maxIter * 360, 1, i / maxIter)
img[y,x] = RGB{Float64}(r, g, b)
end
end
save("mandelbrot_set2.png", img)
end
mandelbrot()
и еще ряд интересных правил:


Магистрали довольно частое явление

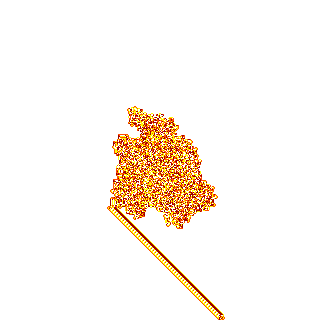


Мозг в ящике — довольно стабильная структура. Здесь результат тридцати миллиардов шагов:





Короче, с такого рода экспериментами можно засесть надолго. И это мы только комбинировали два направления (лево-право), а ведь можно добавить еще вперед-назад, к тому же, никто не говорил, что муравей обязан продвигаться на одну клетку! Держу пари, что такого рода расширение стандартных правил породит еще много интересных закономерностей!
Эпилог
К слову о жизни. Немало интереса вызывают самовоспроизводящиеся структуры, а ля циклы Лэнгтона

Можно почитать статью, где данную модель расширяют наличием пола и передачей генов. (Тут уж передаю эстафету кому-нибудь другому. Очень хотелось бы посмотреть на реализацию подобной штуки)
Тема клеточных автоматов с ростом вычислительных мощностей и улучшением алгоритмов становится все популярней. У Вольфрама в блоге небольшой отчет по этой теме, да и каждый может сам убедиться — статей много, причем самых разнообразных: там вам и дружба с нейронными сетями, и генераторы случайных чисел, и квантовые точки, и сжатие и много всякого другого...
Ну и напоследок самокопирующаяся структура созданная Тэдом Коддом на спор за пинту пива