источник изображения

Возможно, вы видели предыдущий пост, где были предоставлены визуализации первых 1000 цифр $$ и $$. Он возник в результате небольшого спора о том, лучше ли $$, чем $$. По этому поводу идут бесконечные дебаты, и я подумал, что могу пошутить по этому поводу. В этом посте я хочу показать, как создать визуализации, и надеюсь, что вы захотите попробовать удивительный пакет Luxor.jl после прочтения. Вчера я начал читать туториал, и это потрясающе! В прошлый раз визуализация делалась на Javascript, и я подумал, что этот аккуратный маленький проект сойдет, чтобы начать изучать Луксор. Как уже упоминалось в let me be your mentor: я думаю, что очень важно иметь такие маленькие проекты, чтобы освоить новый инструмент.

Основная идея

Я хотел воссоздать визуализацию, которую видел в Numberphile от Мартина Крживинского.

Там был круг (который, вполне ассоциируется и с $$ и с $$) разделенный на 10 сегментов, по одному для каждой цифры. Цифры нашего иррационального числа представляются кривыми внутри этого круга, так что 3.1415 (я начинаю с 14) — это кривая от сегмента 1 до сегмента 4, а затем обратно к 1, потом до 5 и так далее. Каждый раз мы перемещаемся немного по часовой стрелке в сегменте так, что 1>4 создает различные кривые (в зависимости от текущего положения, в котором мы находимся).

Потом надобавляем всякие фичи. Мы должны начать чувствовать себя комфортно с Луксором. Важно: не надо искать математическую интерпретацию — это просто небольшой проект визуализации ;)

Я знаю, вам интересно, как должен выглядеть конечный результат:

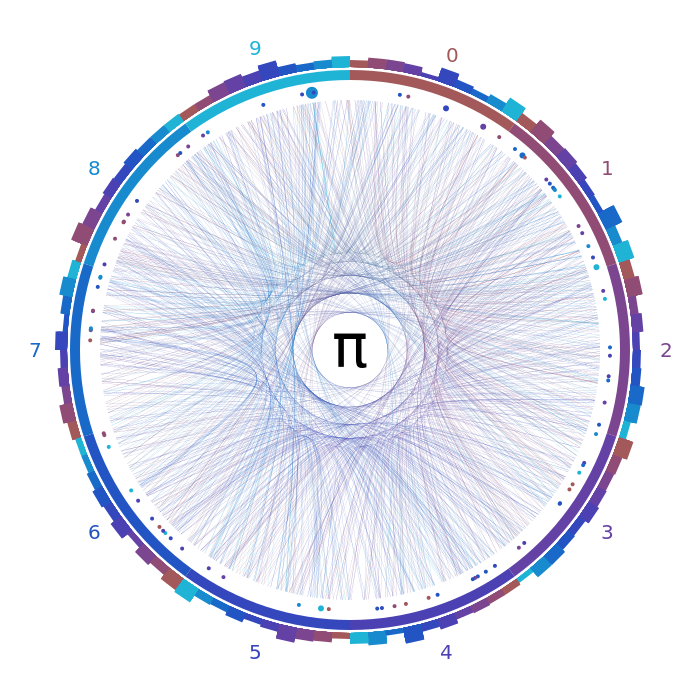
Начинаем

using Luxor

function vis()
    @png begin
        sethue("black")
        circle(O, 50, :stroke)
        setdash("dot")
        circle(O, 70, :stroke)
        sethue("darkblue")
        circle(O, 10, :fill)

    end 500 200 "./start.png"
end

вызываем vis() и создаем файл start.png который будет выглядеть как-то так:

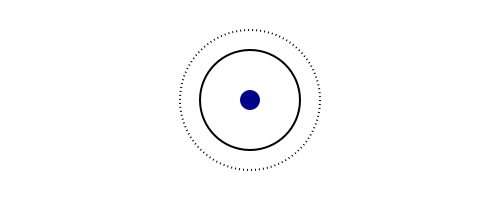
Давайте быстренько пройдемся по командам:

@png begin
end width height "filename.png"

просто хороший макрос. :)

sethue задает цвет и принимает либо строку, как показано выше или цвет пакета из Colors. Он устанавливает цвет для следующих команд рисования до тех пор, пока вы не выберете другой. То же самое верно и при установке ширины линии с помощью setline, или при установке размера шрифта, или при других общих настройках.

Команды рисования, такие как circle, обычно принимают некоторые параметры и заканчиваются параметром действия, таким как :stroke или :fill.

О — это буква "О", а не число "0". :) Она представляет собой начало координат и является краткой формой для Point(0, 0). В Луксоре начало находится в центре полотна. В качестве второго параметра должен быть задан радиус.

Давайте сначала нарисуем внешний круг и добавим цифры:

radius = 100
@png begin
    background("black")

    sethue("white")
    circle(O, radius, :stroke)

    for i in 0:9
        ? = 2?*0.1*i+0.1*?
        mid = Point(
            radius*sin(?),
            -radius*cos(?),
        )
        label(string(i), :N, mid)
    end

end 700 300 "./first_step.png"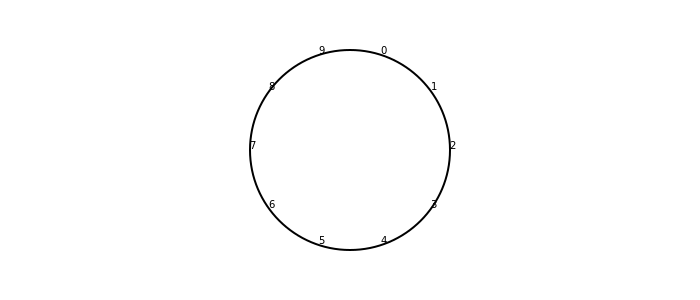

Первая часть должна быть достаточно простой.

? = 2?*0.1*i+0.1*?

возможно, это не идеально написано (кроме того, я мог бы использовать $$ :D). 2?*0.1*i начинает с северного положения, а затем для следующего i происходит перемещение на $$. Я добавляю "0.1 ?", потому что хочу переходить к середине каждого сегмента. Может быть, следует написать 0.5/10*2?. Затем мы просто поворачиваем наш холст и двигаясь чуть выше радиуса, рисуем метки. На самом деле такое можно проделать в Luxor, используя rotate и translate. Но я решил сделать вручную, так как мне все равно это пригодится позже. В общем формула такова:

Такое преобразование поворачивает плоскость на $$ и производит трансляцию на x,y. Поскольку я перевожу только на y, мне не нужно первое тождество. Помните, что y увеличивается, когда идет вниз.

В настоящее время есть две проблемы:

• на самом деле нам не нужен круг, нам нужны дуги (сегменты) для каждой цифры
• подписи не читаются

Команда label принимает три значения: текст, вращение и положение, где вращение может быть записано как :N,: E,: S,: W для севера, востока, юга, запада или как угол (в радианах). :N есть $$. Поэтому мы хотим начать с $$, а потом добавлять текущий угол поворота. Кроме того, смещение было бы здорово, если бы оно не доставало непосредственно до окружности или не подходило слишком близко к ней. Здесь мы могли бы увеличить радиус или использовать ;offset в команде label.

Для первой задачи нам нужна функция arc2r, которая принимает три аргумента
c1, p1, p2 + действие: c1 — это центр окружности, а p1 и p2 — точки на окружности, между которыми должен быть показан сегмент. По умолчанию выбрано направление по часовой стрелке.

Мы определяем следующую функцию, чтобы получить $$ и соответствующую точку более простым способом:

function get_coord(val, radius)
    ? = 2?*0.1*val
    return Point(
        radius*sin(?),
        -radius*cos(?),
    )
end

а потом:

background("black")

for i in 0:9
    from = get_coord(i, radius)
    to = get_coord(i+1, radius)
    randomhue()

    ? = 2?*0.1*i+0.1*?
    mid = Point(
        radius*sin(?),
        -radius*cos(?),
    )
    label(string(i), -?/2+?, mid; offset=15)
    move(from)
    arc2r(O, from, to, :stroke)
end

Я использовал randomhue, чтобы получить случайный цвет. Мы исправим это в следующий раз :)
Также я переставлял порядок Label и arc2r и поставил move, так как в противном случае линии рисуются от метки дуги. Это происходит потому, что arc продолжает текущий путь.

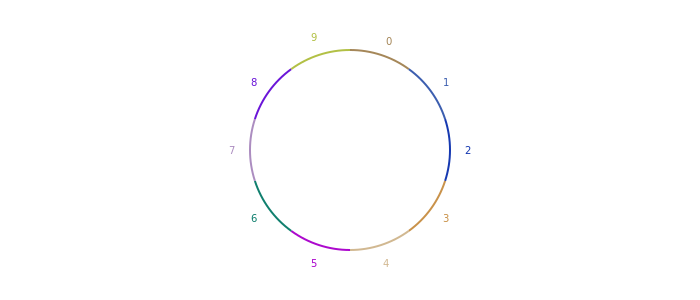
Выглядит намного лучше! Давайте возьмем несколько хороших цветов из Colorschemes.jl.

Я использовал схему rainbow, начиная с 7-го цвета :D. Вы, возможно, захотите испытать другие цветовые схемы, так как здесь цвета не так легко различить, но мне все равно почему-то нравится именно она.

using ColorSchemes
colors = ColorSchemes.rainbow[7:end]

и затем

sethue(colors[i+1])

помните, что индексация массивов в Julia начинается с единицы.

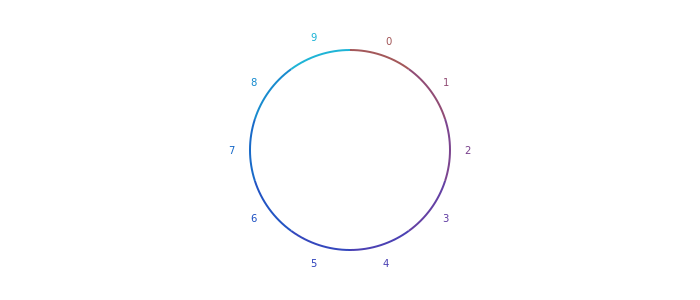
Каковы следующие шаги?

• Добавление строк
• Рефакторинг кода
• Оживление процесса
• Добавление точек
• Добавление гистограммы сверху

Я думаю, что визуально привлекательно иметь круг посередине, где мы можем добавить символ $$ (или $$) позже.
Поэтому мы не можем провести прямые линии от одного сегмента к другому. Для этого я использую квадратичные кривые Безье.

Давайте сначала получим цифры числа Пи:

max_digits = 10
digits = setprecision(BigFloat, Int(ceil(log2(10) * max_digits+10))) do
    return parse.(Int, collect(string(BigFloat(pi))[3:max_digits+2]))
end

это дает нам первые 10 цифр после десятичной точки числа Пи. Для этого мне нужно установить точность BigFloat. Довольно интересно, что пи не является жестко закодированной константой в Джулии. Оно вычислено таким образом, что я в принципе могу получить любую точность, какую захочу. Точность должна быть задана в количестве битов, так что необходимо выполнить небольшое вычисление. Я добавил +10 в конце, чтобы быть уверенным :D

Чтобы нарисовать квадратичную кривую Безье, нам нужны три точки. Начало, конец и контрольная точка. В качестве контрольной точки я выбираю точку на внутреннем круге, который просто также разделен на десять сегментов, и выбираю сегмент, который находится посередине между текущей цифрой from_val и следующей цифрой to_val.

Я должен уточнить, что я имею в виду под серединой: средняя точка между 0 и 4 должна быть 2, но между 8 и 0 она должна быть 9. Она определяется кратчайшим путем от одного сегмента к другому, а потом берется середина.

Кроме того, у меня на самом деле нет 10 дискретных сегментов, это просто для понимания. Я могу использовать среднюю точку 1,23 или что-то в этом роде. Это используется, потому что мы меняем нашу начальную и конечную позиции на основе текущей позиции, которую мы находимся в нашем массиве цифр.

Я надеюсь, что все станет яснее, ели взглянуть на код:

small_radius = 70
for i in 1:max_digits-1
    from_val = digits[i]
    to_val = digits[i+1]
    sethue(colors[from_val+1])

    f = from_val+(i-1)/max_digits
    t = to_val+i/max_digits

    from = get_coord(f, radius)
    to = get_coord(t, radius)

    # get the correct mid point for example for 0-9 it should be 9.5 and not 4.5
    mid_val = (f+t)/2
    mid_control = get_coord(mid_val, small_radius)
    if abs(f-t) >= 5
        mid_control = get_coord(mid_val+5, small_radius)
    end

    pts = Point[from, mid_control, mid_control, to]
    bezpath = BezierPathSegment(pts...)
    drawbezierpath(bezpath, :stroke, close=false)
end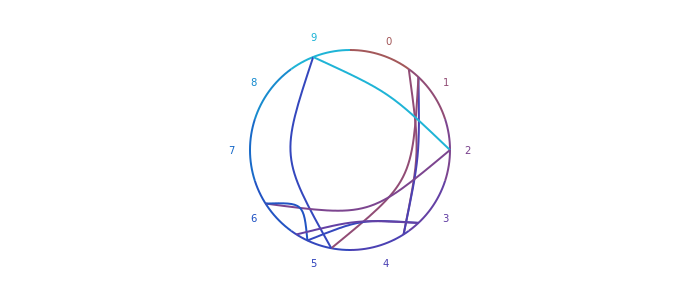

Думаю, уже выглядит достаточно хорошо. Цвета линий подгоняются под цвета из под цифр. Итак, в какой-то момент мы переходим от 9 к 2. Вместо этого я хотел бы посмотреть, куда мы идем и откуда идем. Это можно сделать с помощью blend и setblend. Это линейная смена цвета "от" и "до", так что на самом деле не по кривой, но я думаю, что она достаточно хороша.

setblend(blend(from, to, colors[to_val+1], colors[from_val+1]))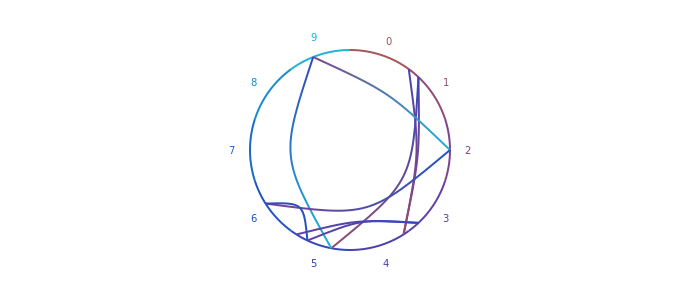

Это похоже на sethue поэтому нам нужно задать его в какой-то момент, прежде чем мы вызовем drawbezierpath.

Давайте добавим еще несколько цифр и немного уменьшим ширину линии: setline(0.1)

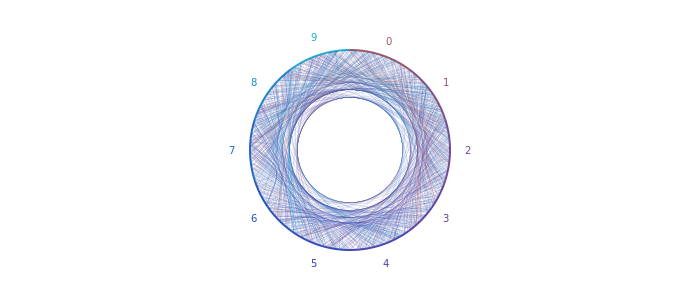
Ладно я думаю что внутренний радиус немного велик:

small_radius = 40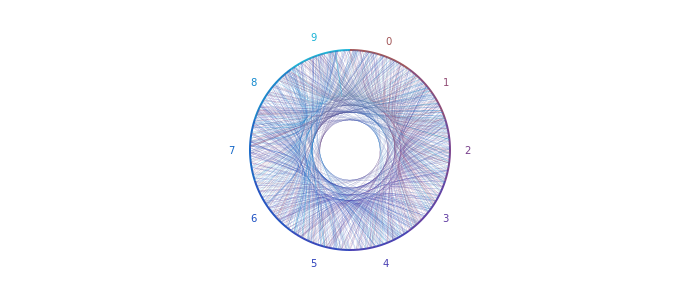

Затем мы можем добавить $$ в середине, прежде чем немного очистить код, чтобы создать нашу первую анимацию.

Luxor.jl не поддерживает латексные стринги LaTeXStrings.jl — это облом, но мы можем использовать UnicodeFun.jl.

using UnicodeFun
center_text = to_latex("\\pi")

и промеж циклов ставим:

sethue("white")
fontsize(60)
text(center_text, Point(-2, 0), valign=:middle, halign=:center)

Мне кажется Point(-2, 0) более центральная, чем Point(0, 0) или O.

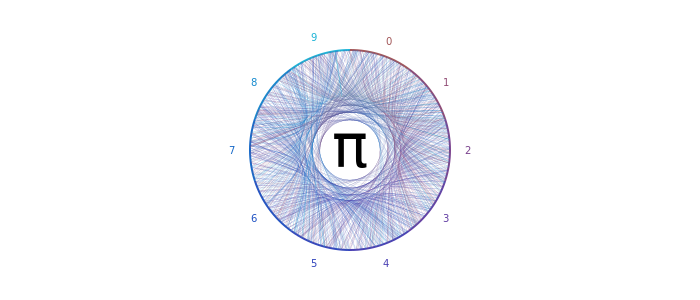
Анимация

Я хотел бы получить gif из конвейера визуализации таким образом, чтобы в каждом кадре добавлялась новая линия.

В Луксоре это можно сделать с помощью функции animate, которая берет несколько сцен и их номера кадров. Это также обеспечит немного большую структуру кода.

У нас может быть сцена для устойчивого фона и одна для линий.

Прежде чем мы напишем функцию, давайте определим очень короткую анимацию, чтобы увидеть, как это делается.

function draw_background(scene, framenumber)
    background("black")
end

function circ(scene, framenumber)
    setdash("dot")
    sethue("white")
    translate(-200, 0)
    @layer begin 
        translate(framenumber*2, 0)
        circle(O, 50, :fill)
    end
end

function anim()
    anim = Movie(600, 200, "test")

    animate(anim, [
        Scene(anim, draw_background, 0:200),
        Scene(anim, circ, 0:200),
    ],
    creategif = true,
    pathname = "./test.gif"
    )
end

Сначала мы создаем Movie с width, height и name.
Затем мы вызываем animate с помощью созданного Movie и списка scenes, а затем функции и диапазон кадров, начинающихся с 0.

Происходит вызов draw_background(сцена, 0) и circ(scene, 0) для первого кадра. Сцена может содержать некоторые аргументы, которые мы будем использовать для нашей анимации. Остальное в основном так же, как и раньше, просто мы можем, конечно, использовать переменную framenumber.

Теперь я разделю все это дело на функции и определю переменные, такие как цифры, которые мы хотим визуализировать, чтобы нам было легче визуализировать $$ или другие вещи.

using Luxor, ColorSchemes
using UnicodeFun

function get_coord(val, radius)
    ? = 2?*0.1*val
    return Point(
        radius*sin(?),
        -radius*cos(?),
    )
end

function draw_background(scene, framenumber)
    background("black")

    radius = scene.opts[:radius]
    colors = scene.opts[:colors]
    center_text = scene.opts[:center_text]

    for i in 0:9
        from = get_coord(i, radius)
        to = get_coord(i+1, radius)
        sethue(colors[i+1])

        ? = 2?*0.1*i+0.1*?
        mid = Point(
            radius*sin(?),
            -radius*cos(?),
        )
        label(string(i), -?/2+?, mid; offset=15)
        move(from)
        arc2r(O, from, to, :stroke)
    end

    sethue("white")
    fontsize(60)
    text(center_text, Point(-2, 0), valign=:middle, halign=:center)
end

function dig_line(scene, framenumber)
    radius = scene.opts[:radius]
    colors = scene.opts[:colors]
    center_text = scene.opts[:center_text]
    bezier_radius = scene.opts[:bezier_radius]
    max_digits = scene.opts[:max_digits]
    digits = scene.opts[:digits]

    setline(0.1)

    for i in 1:min(framenumber, max_digits-1)
        from_val = digits[i]
        to_val = digits[i+1]

        f = from_val+(i-1)/max_digits
        t = to_val+i/max_digits

        from = get_coord(f, radius)
        to = get_coord(t, radius)

        # get the correct mid point for example for 0-9 it should be 9.5 and not 4.5
        mid_val = (f+t)/2
        mid_control = get_coord(mid_val, bezier_radius)
        if abs(f-t) >= 5
            mid_control = get_coord(mid_val+5, bezier_radius)
        end

        pts = Point[from, mid_control, mid_control, to]
        bezpath = BezierPathSegment(pts...)
        # reverse the color to see where it is going
        setblend(blend(from, to, colors[to_val+1], colors[from_val+1]))
        drawbezierpath(bezpath, :stroke, close=false)
    end
end

function anim()
    anim = Movie(700, 300, "test")

    radius = 100
    bezier_radius = 40
    colors = ColorSchemes.rainbow[7:end]
    max_digits = 1000
    center_text = to_latex("\\pi")

    digits_arr = setprecision(BigFloat, Int(ceil(log2(10) * max_digits+10))) do
        return parse.(Int, collect(string(BigFloat(pi))[3:max_digits+2]))
    end

    args = Dict(:radius => radius,
        :bezier_radius => bezier_radius,
        :colors => colors, :max_digits => max_digits,
        :digits => digits_arr, :center_text => center_text
    )

    animate(anim, [
        Scene(anim, draw_background, 0:max_digits+50, optarg=args),
        Scene(anim, dig_line, 0:max_digits+50, optarg=args),
    ],
    creategif = true,
    pathname = "./pi_first.gif"
    )
end

Единственное, что я еще не объяснил, — это optarg в функции Scene и получение его с помощью radius = scene.opts[:radius].

Мы как бы потеряли возможность создавать простые образы. Поэтому я создал структуру

struct PNGScene
    opts::Dict{Symbol, Any}
end

и использую некоторые аргументы в функции anim, которую я переименую в viz :D

Тогда я могу использовать что-то вроде:

scene = PNGScene(args)
@png begin
    draw_background(scene, max_digits)
    dig_line(scene, max_digits)
end 700 300 "./$fname.png"

Не волнуйтесь, в конце есть репка, где вы можете увидеть весь код целиком. Просто немного сложно описать здесь изменения.

Может, мне стоило снять видео? :D

Добавление точки Фейнмана

Мы визуализировали соединение цифр с цифрами с помощью кривых, но если бы у нас встретилось что-то вроде 555 в цифрах, мы бы видели только линию, идущую в направлении центра и обратно (или, может быть, мы видим две в зависимости от наших максимальных цифр, разрешения и т. д.)

Вместо этого мы можем показать дополнительную точку всякий раз, когда это происходит. Это можно получить благодаря аргументу функции show_dots, что вы можете найти в моем коде ;)

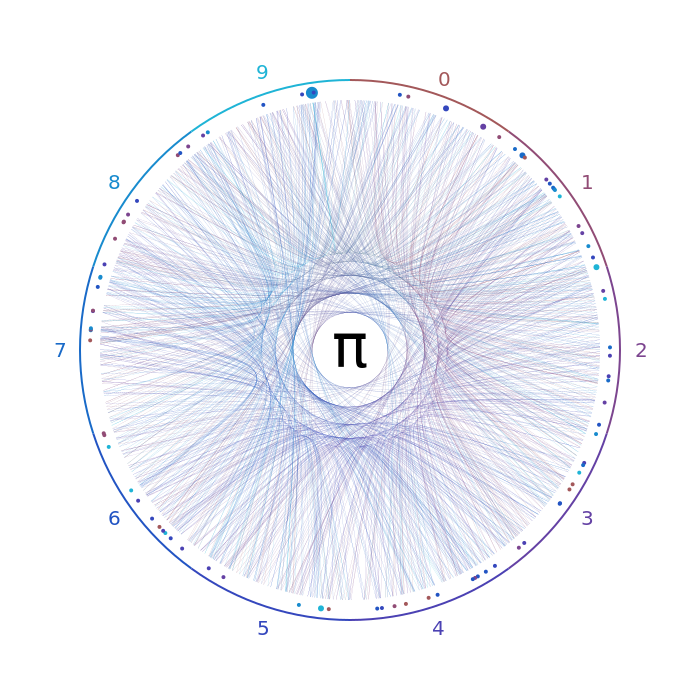
Я только что проверил длину последовательности, и когда она больше 1, я рисую круг, где это происходит, и цвет — это цифра после этой последовательности. Большой круг в сегменте 9 — это так называемая точка Фейнмана, где цифра 9 появляется 6 раз в позиции 762.

Добавление гистограмм

Последняя вещь в моем списке — получить гистограмму на каждом сегменте, чтобы показать, случаются ли некоторые комбинации пар чаще, чем другие.

Для этого я использую функцию poly с четырьмя точками. В идеале, она должна быть ограничена двумя дугами, а не двумя линиями, но я оставляю это читателю :)

Тау

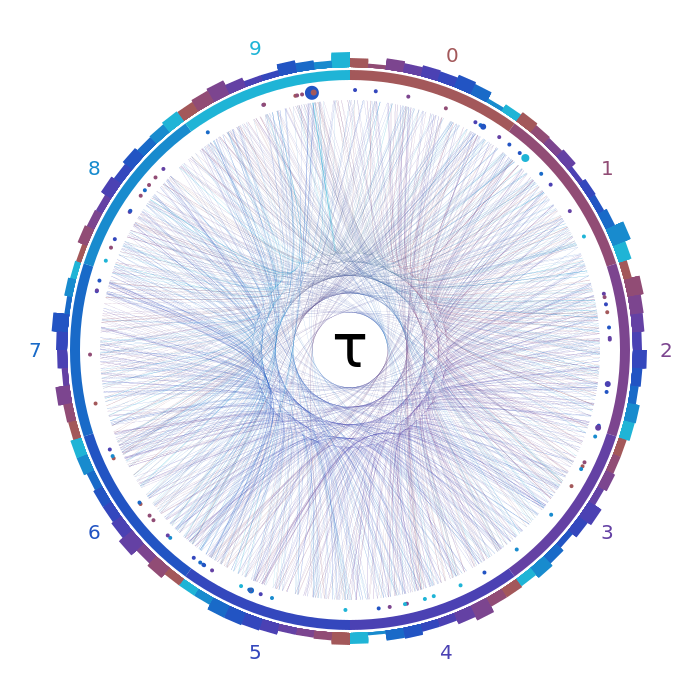
Да, можно было бы в принципе сгенерировать случайное число с 1000 цифрами и получить аналогичный результат...

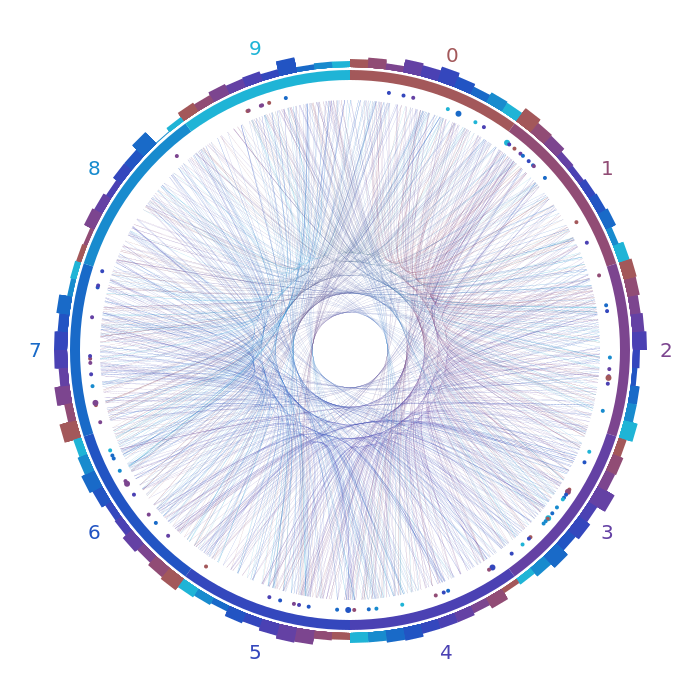
Простое число

В двух словах: использование нашей функции для визуализации большинства элементов не так разумно, но так или иначе может получится что-то интересное.

При этом в качестве числовой последовательности используются последние цифры простых чисел. Я визуализировал простые числа меньше 100 000. Честно говоря, соединительные линии немного бесполезны, так как большую часть времени (если мы игнорируем первые несколько простых чисел: все время) возможны только четыре цифры. Это создает своего рода беспорядок в середине.

Тем не менее, гистограммы становятся все интереснее, я думаю:

Это ясно показывает, что не все пары одинаково вероятны. Особенно, если у нас есть простое число $$ с последней цифрой x, то всегда менее вероятно, что последняя цифра $$ также заканчивается на x по сравнению с одним из трех других вариантов.

Давайте сосредоточимся на гистограммах и визуализируем простые числа под 10 000 000:

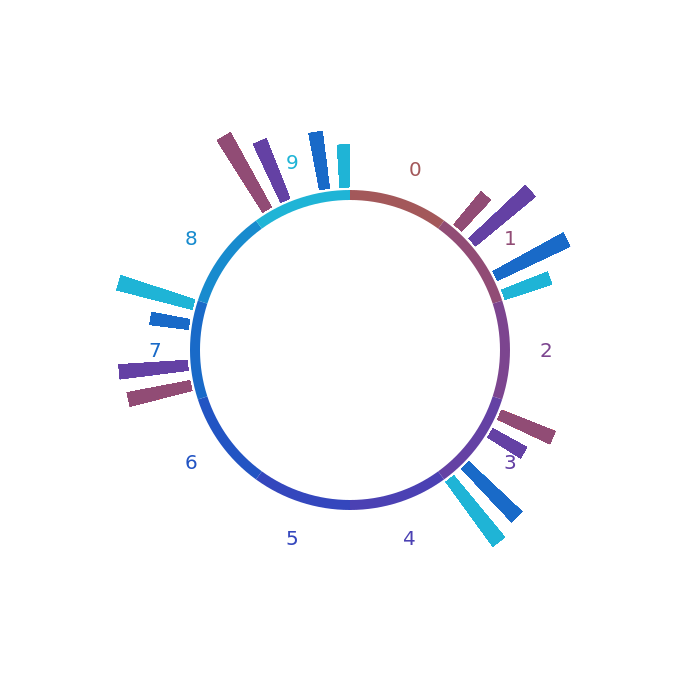
Узор сохраняется.

Код

Окай, тут у нас репка

Я хотел бы создать что-то вроде штучек, из 3b1b.

По крайней мере, небольшие простые версии с некоторыми удобными функциями визуализации :)

Спасибо за чтение и особая благодарность моим 10 покровителям!

Я буду держать вас в курсе событий на Twitter OpenSourcES и на более личном:
Twitter Wikunia_de