
Экспериментируя с простейшей задачкой машинного обучения я обнаружил, что интересно было бы подобрать в довольно широком диапазоне значения 18 гиперпараметров одновременно. В моём случае всё было на столько несложно, что задачку можно было бы взять и грубой компьютерной силой.
Обучаясь чему-то мне бывает очень интересно изобрести какой-нибудь велосипед. Иногда получается реально придумать что-то новое. Иногда обнаруживается, что все придумано до меня. Но даже если я всего лишь повторю путь пройденный за долго до меня, в награду я часто получаю понимание глубинных механизмов алгоритмов их возможностей и внутренних ограничений. К чему и вас приглашаю.
В Python и DS я, сказать мягко, новичок, и многие вещи, которые можно реализовать в одну команду по своей старой программистской привычке делаю кодом, за что Python наказывает замедлением даже не в разы, а на порядки. Поэтому весь свой код я выкладываю в репозиторий. Если знаете как реализовать сильно эффективнее — не стесняйтесь, правьте там, или пишите в комментариях. https://github.com/kraidiky/GDforHyperparameters
Тем, кто уже крутой датасатанист, и всё в этой жизни попробовал небезинтересна будет, я полагаю, визуализация процесса обучения, которая применима не только к этой задачке.
Постановка задачи
Есть такой хороший курс по DS от ODS.ai и там третья лекция Классификация, деревья решений и метод ближайших соседей. Там на предельно простых и, вероятно, синтетических данных показывается как простейшее дерево решений даёт точность 94.5%, а такой же предельно простой метод k ближайших соседей без всякой предобработки даёт 89%
Импорт и загрузка данных
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
df = pd.read_csv('data/telecom_churn.csv')
df['Voice mail plan'] = pd.factorize(df['Voice mail plan'])[0]
df['International plan'] = pd.factorize(df['International plan'])[0]
df['Churn'] = df['Churn'].astype('int32')
states = df['State']
y = df['Churn']
df.drop(['State','Churn'], axis = 1, inplace=True)
df.head()
Сравнение дерева с knn
%%time
from sklearn.model_selection import train_test_split, StratifiedKFold
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV, cross_val_score
from sklearn.metrics import accuracy_score
X_train, X_holdout, y_train, y_holdout = train_test_split(df.values, y, test_size=0.3,
random_state=17)
tree = DecisionTreeClassifier(random_state=17, max_depth=5)
knn = KNeighborsClassifier(n_neighbors=10)
tree_params = {'max_depth': range(1,11), 'max_features': range(4,19)}
tree_grid = GridSearchCV(tree, tree_params, cv=10, n_jobs=-1, verbose=False)
tree_grid.fit(X_train, y_train)
tree_grid.best_params_, tree_grid.best_score_, accuracy_score(y_holdout, tree_grid.predict(X_holdout))
({'max_depth': 6, 'max_features': 16}, 0.944706386626661, 0.945)
то же для knn
%%time
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
knn_pipe = Pipeline([('scaler', StandardScaler()), ('knn', KNeighborsClassifier(n_jobs=-1))])
knn_params = {'knn__n_neighbors': range(1, 10)}
knn_grid = GridSearchCV(knn_pipe, knn_params, cv=10, n_jobs=-1, verbose=False)
knn_grid.fit(X_train, y_train)
knn_grid.best_params_, knn_grid.best_score_, accuracy_score(y_holdout, knn_grid.predict(X_holdout))
({'knn__n_neighbors': 9}, 0.8868409772824689, 0.891)
На этом месте мне стало обидно за knn явно поставленный в нечестные условия, ведь с метрикой длинны мы никак не поработали. Я не стал думать мозгом, взял feature_importances_ у дерева и отнормировал входные данные на него. Таким образом, Чем фича важнее тем больше её вклад расстояние между точками.
Скармливаем данные отнормированные на важность фич
%%time
feature_importances = pd.DataFrame({'features': df.columns, 'importance':tree_grid.best_estimator_.feature_importances_})
print(feature_importances.sort_values(by=['importance'], inplace=False, ascending=False))
scaler = StandardScaler().fit(X_train)
X_train_transformed = scaler.transform(X_train)
X_train_transformed = X_train_transformed * np.array(feature_importances['importance'])
X_holdout_transformed = scaler.transform(X_holdout)
X_holdout_transformed = X_holdout_transformed * np.array(feature_importances['importance'])
knn_grid = GridSearchCV(KNeighborsClassifier(n_jobs=-1), {'n_neighbors': range(1, 11, 2)}, cv=5, n_jobs=-1, verbose=False)
knn_grid.fit(X_train_transformed, y_train)
print (knn_grid.best_params_, knn_grid.best_score_, accuracy_score(y_holdout, knn_grid.predict(X_holdout_transformed)))
| 5 | Total day minutes | 0.270386 |
| 17 | Customer service calls | 0.147185 |
| 8 | Total eve minutes | 0.135475 |
| 2 | International plan | 0.097249 |
| 16 | Total intl charge | 0.091671 |
| 15 | Total intl calls | 0.090008 |
| 4 | Number vmail messages | 0.050646 |
| 10 | Total eve charge | 0.038593 |
| 7 | Total day charge | 0.026422 |
| 3 | Voice mail plan | 0.017068 |
| 11 | Total night minutes | 0.014185 |
| 13 | Total night charge | 0.005742 |
| 12 | Total night calls | 0.005502 |
| 9 | Total eve calls | 0.003614 |
| 6 | Total day calls | 0.002246 |
| 14 | Total intl minutes | 0.002009 |
| 0 | Account length | 0.001998 |
| 1 | Area code | 0.000000 |
{'n_neighbors': 5} 0.909129875696528 0.913
Дерево всего чуть-чуть поделилось с knn своими знаниями и вот мы видим уже 91% Что уже не так далеко от 94.5% у ванильного дерева. И вот тут меня и посетила идея. А как, собственно, надо отнормировать входные данные чтобы knn показала наилучший результат?
Сначала прикинем в уме сколько вот это вот будет считаться «в лоб». 18 параметров, для каждого сделаем, допустим, 10 возможных ступеней множителей в логарифмической шкале. Получаем 10е18 вариантов. Один вариант со всем возможным нечётным количеством соседей меньше 10 и кроссвалидацией тоже 10 у меня считается примерно 1.5 секунды. Получается 42 млрд. лет. От идеи оставить считаться на ночь придётся, пожалуй, отказаться. :) И вот где-то тут я подумал «Эй! Так я ща сделаю велосипед, который полетит!»
Околоградиентный поиск
Вообще-то у этой задачи, скорее всего, всего один доступный максимум. Ну тоесть не один конечно, целая область неплохих результатов, но они довольно сильно похожи друг на друга. Поэтому мы можем просто пройти по градиенту и найти наиболее подходящую точку. Первая мысль была вообще генетический алгоритм запилить, но здесь адаптивный рельеф представляется не сильно пересечённым, и это был бы уже немножечко перебор.
Попробую сделать это вручную для начала. Чтобы запихивать множетели в качестве гиперпараметров мне потребуется разобраться со скейлерами. В прошлом примере я, как и в уроке, применил StandartScaler, который учебную выборку отцентровал по среденму и сделал sigma = 1. Для того чтобы её красиво масштабировать внутри пайплайна гиперпараметром придётся сделать чуть-чуть хитрее. Я начал искать среди преобразователей лежищих в sklearn.preprocessing что-то подходящее к моему случаю, но ничего не нашёл. Поэтому я попытался отнаследоваться от StandartScaler навешав на него дополнительную пачку множителей.
Класс для номализации а потом умножения на масштаб слегка совместимый с пайплайном sklearn
from sklearn.base import TransformerMixin
class StandardAndPoorScaler(StandardScaler, TransformerMixin):
#normalization = None
def __init__(self, copy=True, with_mean=True, with_std=True, normalization = None):
#print("new StandardAndPoorScaler(normalization=", normalization.shape if normalization is not None else normalization, ") // ", type(self))
self.normalization = normalization
super().__init__(copy, with_mean, with_std)
def fit(self, X, y=None):
#print(type(self),".fit(",X.shape, ",", y.shape if y is not None else "<null>",")")
super().fit(X, y)
return self
def partial_fit(self, X, y=None):
#print(type(self),".partial_fit(",X.shape, ",", y.shape if y is not None else "<null>)")
super().partial_fit(X, y)
if self.normalization is None:
self.normalization = np.ones((X.shape[1]))
elif type(self.normalization) != np.ndarray:
self.normalization = np.array(self.normalization)
if X.shape[1] != self.normalization.shape[0]:
raise "X.shape[1]="+X.shape[1]+" in equal self.scale.shape[0]="+self.normalization.shape[0]
def transform(self, X, copy=None):
#print(type(self),".transform(",X.shape,",",copy,").self.normalization", self.normalization)
Xresult = super().transform(X, copy)
Xresult *= self.normalization
return Xresult
def _reset(self):
#print(type(self),"._reset()")
super()._reset()
scaler = StandardAndPoorScaler(normalization = feature_importances['importance'])
scaler.fit(X = X_train, y = None)
print(scaler.normalization)
Попытка этот класс применить
%%time
knn_pipe = Pipeline([('scaler', StandardAndPoorScaler()), ('knn', KNeighborsClassifier(n_jobs=-1))])
knn_params = {'knn__n_neighbors': range(1, 11, 4), 'scaler__normalization': [feature_importances['importance']]}
knn_grid = GridSearchCV(knn_pipe, knn_params, cv=5, n_jobs=-1, verbose=False)
knn_grid.fit(X_train, y_train)
knn_grid.best_params_, knn_grid.best_score_, accuracy_score(y_holdout, knn_grid.predict(X_holdout))
({'knn__n_neighbors': 5, 'scaler__normalization': Name: importance, dtype: float64}, 0.909558508358337, 0.913)
Результат несколько отличается от моих ожиданий. Ну то есть в принципе всё работает. Вот только чтобы это понять, мне пришлось за три часа воспроизвести этот класс со всеми потрохами с нуля, и только тогда я понял, что print нифига не печатает не потому что sklearn как-то неправильно сделан, а потому что GridSearchCV клоны создаёт в основном потоке, а настраивает и обучает их в других потоках. А всё что там печатаешь в других потоках исчезает в небытии. А вот если n_jobs=1 поставить, то все вызовы переопределённых функций показываются как милые. Очень дорогое вышло знание, теперь оно у вас тоже есть, и вы заплатили за него чтением нудной статьи.
Ладно, пошли дальше. Теперь я хочу дать некоторую дисперсию по каждому их параметров, а потом дать её поменьше вокруг наилучшего значения и так пока не получу результат похожий на реальность. Это будет первый грубы бейзлайн того, что должен в итоге получить алгоритм моей мечты.
Сформирую несколько вариантов перевзвешиваний, отличающихся по нескольким параметрам
feature_base = feature_importances['importance']
searchArea = np.array([feature_base - .05, feature_base, feature_base + .05])
searchArea[searchArea < 0] = 0
searchArea[searchArea > 1] = 1
print(searchArea[2,:] - searchArea[0,:])
import itertools
affected_props = [2,3,4]
parametrs_ranges = np.concatenate([
np.linspace(searchArea[0,affected_props], searchArea[1,affected_props], 2, endpoint=False),
np.linspace(searchArea[1,affected_props], searchArea[2,affected_props], 3, endpoint=True)]).transpose()
print(parametrs_ranges) # По пять вариантов значения каждого параметра. Всего 125 комбинаций
recombinations = itertools.product(parametrs_ranges[0],parametrs_ranges[1],parametrs_ranges[1])
variances = []
for item in recombinations: # Не знаю как это вот всё сделать в одну строчку, поэтому будут мои омерзительно медленные в Python циклы.
varince = feature_base.copy()
varince[affected_props] = item
variances.append(varince)
print(variances[0])
print(len(variances))
# Методу knn важно только соотношение, поэтому можно не нормировать вообще или нормировать только при переходе от одной выборки к другой.
Ну вот, набор данных для первого эксперимента готов. Теперь попробую проэкспериментировать с данными, для начала полным перебором получившихся 15 вариантов.
Делаем пробный подбор параметров как в статье
%%time
#scale = np.ones([18])
knn_pipe = Pipeline([('scaler', StandardAndPoorScaler()), ('knn', KNeighborsClassifier(n_neighbors = 7 , n_jobs=-1))])
knn_params = {'scaler__normalization': variances} # 'knn__n_neighbors': range(3, 9, 2),
knn_grid = GridSearchCV(knn_pipe, knn_params, cv=10, n_jobs=-1, verbose=False)
knn_grid.fit(X_train, y_train)
knn_grid.best_params_, knn_grid.best_score_, accuracy_score(y_holdout, knn_grid.predict(X_holdout))Ну и всё плохо, времени потрачена прорва, а результат очень неустойчив. Это и по проверке по X_holdout видно, результат пляшет как в калейдоскопе при незначительных изменениях входных данных. Попробую другой подход. Буду менять только один параметр одновременно но зато с многократно большей дискретизацией.
Меняю одно 4-ое свойство
%%time
affected_property = 4
parametrs_range = np.concatenate([
np.linspace(searchArea[0,affected_property], searchArea[1,affected_property], 29, endpoint=False),
np.linspace(searchArea[1,affected_property], searchArea[2,affected_property], 30, endpoint=True)]).transpose()
print(searchArea[1,affected_property])
print(parametrs_range) # Cканируем по одному параметру, зато плотно.
variances = []
for item in parametrs_range: # Не знаю как это вот всё сделать в одну строчку, поэтому будут мои омерзительно медленные в Python циклы.
varince = feature_base.copy()
varince[affected_property] = item
variances.append(varince)
print(variances[0])
print(len(variances))
# Методу knn важно только соотношение, поэтому можно не нормировать вообще или нормировать только при переходе от одной выборки к другой.
knn_pipe = Pipeline([('scaler', StandardAndPoorScaler()), ('knn', KNeighborsClassifier(n_neighbors = 7 , n_jobs=-1))])
knn_params = {'scaler__normalization': variances} # 'knn__n_neighbors': range(3, 9, 2),
knn_grid = GridSearchCV(knn_pipe, knn_params, cv=10, n_jobs=-1, verbose=False)
knn_grid.fit(X_train, y_train)
knn_grid.best_params_, knn_grid.best_score_, accuracy_score(y_holdout, knn_grid.predict(X_holdout))({'scaler__normalization': 4 0.079957 Name: importance, dtype: float64}, 0.9099871410201458, 0.913)
Ну, и что мы имеем с гуся? Подвижки в одну-две десятые процента на кроссвалиадации, и скачка на пол процента на X_holdout если посмотреть при разных affected_property. Видимо существенно и дешево улучшить ситуацию если начинать с того, что нам даёт дерево невозможно на таких данных. Но допустим, что начальной, заранее известной развесовки у нас нет, и попробуем осуществить то же самое в произвольной точки в цикле малюсенькими шажочками. Очень интересно к чему придём.
Первоначальное наполнение
searchArea = np.array([np.zeros((18,)), np.ones((18,)) /18, np.ones((18,))])
print(searchArea[:,0])
history_parametrs = [searchArea[1,:].copy()]
scaler = StandardAndPoorScaler(normalization=searchArea[1,:])
scaler.fit(X_train)
knn = KNeighborsClassifier(n_neighbors = 7 , n_jobs=-1)
knn.fit(scaler.transform(X_train), y_train)
history_holdout_score = [accuracy_score(y_holdout, knn.predict(scaler.transform(X_holdout)))]Функция чуть-чуть меняющая один параметр (с отладочными логами)
%%time
def changePropertyNormalization(affected_property, points_count = 15):
test_range = np.concatenate([
np.linspace(searchArea[0,affected_property], searchArea[1,affected_property], points_count//2, endpoint=False),
np.linspace(searchArea[1,affected_property], searchArea[2,affected_property], points_count//2 + 1, endpoint=True)]).transpose()
variances = [searchArea[1,:].copy() for i in range(test_range.shape[0])]
for row in range(len(variances)):
variances[row][affected_property] = test_range[row]
knn_pipe = Pipeline([('scaler', StandardAndPoorScaler()), ('knn', KNeighborsClassifier(n_neighbors = 7 , n_jobs=-1))])
knn_params = {'scaler__normalization': variances} # 'knn__n_neighbors': range(3, 9, 2),
knn_grid = GridSearchCV(knn_pipe, knn_params, cv=10, n_jobs=-1, verbose=False)
knn_grid.fit(X_train, y_train)
holdout_score = accuracy_score(y_holdout, knn_grid.predict(X_holdout))
best_param = knn_grid.best_params_['scaler__normalization'][affected_property]
print(affected_property,
'property:', searchArea[1, affected_property], "=>", best_param,
'holdout:', history_holdout_score[-1], "=>", holdout_score, '(', knn_grid.best_score_, ')')
# А вот теперь надо решить как изменить в связи с этим диапазон поиска.
before = searchArea[:, affected_property]
propertySearchArea = searchArea[:, affected_property].copy()
if best_param == propertySearchArea[0]:
print('|<<')
searchArea[0, affected_property] = best_param/2 if best_param > 0.01 else 0
searchArea[2, affected_property] = (best_param + searchArea[2, affected_property])/2
searchArea[1, affected_property] = best_param
elif best_param == propertySearchArea[2]:
print('>>|')
searchArea[2, affected_property] = (best_param + 1)/2 if best_param < 0.99 else 1
searchArea[0, affected_property] = (best_param + searchArea[0, affected_property])/2
searchArea[1, affected_property] = best_param
elif best_param < (propertySearchArea[0] + propertySearchArea[1])/2:
print('<<')
searchArea[0, affected_property] = max(propertySearchArea[0]*1.1 - .1*propertySearchArea[1], 0)
searchArea[2, affected_property] = (best_param + propertySearchArea[2])/2
searchArea[1, affected_property] = best_param
elif best_param > (propertySearchArea[1] + propertySearchArea[2])/2:
print('>>')
searchArea[0, affected_property] = (best_param + propertySearchArea[0])/2
searchArea[2, affected_property] = min(propertySearchArea[2]*1.1 - .1*propertySearchArea[1], 1)
searchArea[1, affected_property] = best_param
elif best_param < propertySearchArea[1]:
print('<')
searchArea[2, affected_property] = searchArea[1, affected_property]*.25 + .75*searchArea[2, affected_property]
searchArea[1, affected_property] = best_param
elif best_param > propertySearchArea[1]:
print('>')
searchArea[0, affected_property] = searchArea[1, affected_property]*.25 + .75*searchArea[0, affected_property]
searchArea[1, affected_property] = best_param
else:
print('=')
searchArea[0, affected_property] = searchArea[1, affected_property]*.25 + .75*searchArea[0, affected_property]
searchArea[2, affected_property] = searchArea[1, affected_property]*.25 + .75*searchArea[2, affected_property]
normalization = searchArea[1,:].sum() #Нормализовать, чтобы параметры не убегали в бесконечность.
searchArea[:,:] /= normalization
print(before, "=>",searchArea[:, affected_property])
history_parametrs.append(searchArea[1,:].copy())
history_holdout_score.append(holdout_score)
changePropertyNormalization(1, 9)
changePropertyNormalization(1, 9)
Я вообще ничего и нигде не оптимизировал, и в итоге следующий решительный шаг у меня чуть не пол часа считался:
Скрытый текст
И вот применяем её в цикле например 40 раз.
%%time
# Первоначальное наполнение
searchArea = np.array([np.zeros((18,)), np.ones((18,)) /18, np.ones((18,))])
print(searchArea[:,0])
history_parametrs = [searchArea[1,:].copy()]
scaler = StandardAndPoorScaler(normalization=searchArea[1,:])
scaler.fit(X_train)
knn = KNeighborsClassifier(n_neighbors = 7 , n_jobs=-1)
knn.fit(scaler.transform(X_train), y_train)
history_holdout_score = [accuracy_score(y_holdout, knn.predict(scaler.transform(X_holdout)))]
for tick in range(40):
for p in range(searchArea.shape[1]):
changePropertyNormalization(p, 7)
print(searchArea[1,:])
print(history_holdout_score)Получившаяся точность от knn: 91.9% Лучше чем когда мы передрали данные у дерева. И на много на много лучше, чем в исходном варианте. Сравним то что у нас получилось с важностью фич по мнению дерева решений:
Визуализация важности фич по мнению knn
feature_importances['knn_importance'] = history_parametrs[-1]
diagramma = feature_importances.copy()
indexes = diagramma.index
diagramma.index = diagramma['features']
diagramma.drop('features', 1, inplace = True)
diagramma.plot(kind='bar');
plt.savefig("images/pic1.png", format = 'png')
plt.show()
feature_importances

Похоже? Да, похоже. Но далеко не идентично. Интересное наблюдение. В наборе данных есть несколько фич полностью друг друга дублирующих например 'Total night minutes' и 'Total night charge'. Так обратите внимание, knn сама выпилила значительную часть таких повторяющихся фич.
Сохраним полученные результаты в файл, а то несколько неудобно возвращаться к работе....
parametrs_df = pd.DataFrame(history_parametrs)
parametrs_df['scores'] = history_holdout_score
parametrs_df.index.name = 'index'
parametrs_df.to_csv('parametrs_and_scores.csv')
Выводы
Ну что же, Результат .919 сам по себе не плох для knn, ошибок в полтора раза меньше, чем в ванильной версии и на 7% меньше, чем когда feature_importance мы взяли у дерева погонять. Но самое интересное, что теперь у нас есть feature_importance по мнению самого knn. Он несколько отличается от того, что нам сказало дерево. Например дерево и knn имеют разные мнения о том, какие из признаков для нас вообще не важны.
Ну и в конце концов. Мы получили что-то условно говоря новое и необычное, обладая запасом знания трёх лекций mlcourse.ai
ods и гуглом для ответов на простые вопросы по питону. По-моему неплохо.
А теперь слайды
Побочным продуктом работы алгоритма является путь, который он прошёл. Путь, правда, 18-мерный, что немножечко мешает его осознанию, ну и следить в рельном времени что там алгоритм делает, учится или фигнёй занят, не так удобно. По графику ошибки это, на самом деле, не всегда видно. Ошибка может долгое время не меняться сколько-нибудь заметно, а алгоритм между тем очень занят, ползёт вдоль длинной узкой долины в адаптивном пространстве. Поэтому я применю, для начала, первый простейший но достаточно информативный подход — произвольным случайным образом спроецирую 18-мерное пространство на двумерное так чтобы вклады всех параметров вне зависимости от их значимости были единичными. На самом деле 18-мерный путь это очень мало, в своей статье Подглядываем за метаниями нейронной сети я подобным же образом любовался за пространством весов всех имеющихся у нейросети синапсов и ничё так, было красиво и информативненько.
Прочитал данные из файла, если возвращаюсь к работе миновав собственно этап обучения
parametrs_df = pd.read_csv('parametrs_and_scores.csv', index_col = 'index')
history_holdout_score = np.array(parametrs_df['scores'])
parametrs_df.drop('scores',axis=1)
history_parametrs = np.array(parametrs_df.drop('scores',axis=1))Ошибка на валидации перестаёт меняться c какого-то момента. Тут бы можно было вкрутить автоматический останов обучения и пользоваться полученной функцией всю оставшуюся жизнь, но мне уже немножечко некогда. :(
Определяем сколько нужно было учиться.
last = history_holdout_score[-1]
steps = np.arange(0, history_holdout_score.shape[0])[history_holdout_score != last].max()
print(steps/18)35.55555555555556
За раз мы меняли по одному параметру, так что один цикл оптимизации — 18 шагов. Получается у нас было 36 осмысленных шагов, или что-то около того. Теперь попробуем визуализировать траекторию по которой обучался метод.
Скрытый текст
%%time
# Задаём произвольные единичные проекции:
import matplotlib.pyplot as plt
%matplotlib inline
import random
import math
random.seed(17)
property_projection = np.array([[math.sin(a), math.cos(a)] for a in [random.uniform(-math.pi, math.pi) for i in range(history_parametrs[0].shape[0])]]).transpose()
history = np.array(history_parametrs[::18]) # Полный цикл - 18 параметров.
# Мне мозгов не зватает чтобы одно на другое помножить без циклов. :(
points = np.array([(history[i] * property_projection).sum(axis=1) for i in range(history.shape[0])])
plt.plot(points[:36,0],points[0:36,1]);
plt.savefig("images/pic2.png", format = 'png')
plt.show()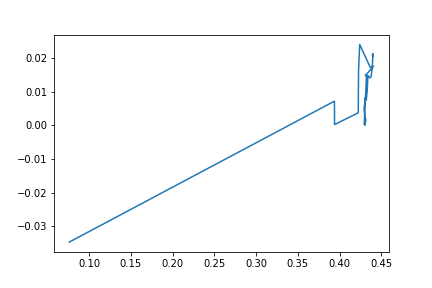
Видно, что значительную часть пути обучение прошло за первых четыре шага. Посмотрим на весь остальной путь с увеличением
Без первых 4-х точек
plt.plot(points[4:36,0],points[4:36,1]);
plt.savefig("images/pic3.png", format = 'png')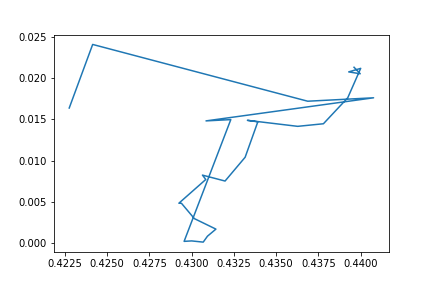
Приблизим заключительную часть пути и посмотрим что обучалка делала после того как достигла своего пункта назначения.
приближаемся
plt.plot(points[14:36,0],points[14:36,1]);
plt.savefig("images/pic4.png", format = 'png')
plt.show()
plt.plot(points[24:36,0],points[24:36,1]);
plt.plot(points[35:,0],points[35:,1], color = 'red');
plt.savefig("images/pic5.png", format = 'png')
plt.show()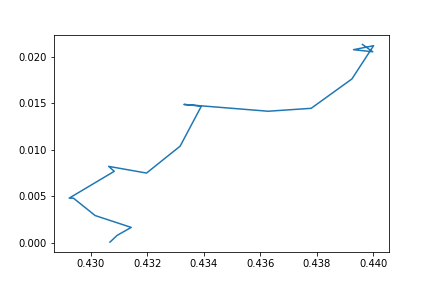

Видно, что алгоритм сосредоточенно обучается. Пока не находит свою пункт назначения. Конкретная точка, конечно, от рандома при кроссвалидации зависит. Но вне зависимости от конкретной точки общая картина происходёщего понятна.
Я, кстати, раньше использовал такой график для демонстрации процесса обучения.
Показывается не вся траектория а последние сколь-ко то шагов со скользящим сглаживанием масштаба. Пример можно посмотреть в другой моей статье «Подглядываем за метаниями нейронной сети». И да, конечно, каждый кто сталкивается с такой визуализацией сразу спрашивает, а почему у всех факторов одинаковый вес, важность, то у них разная. В прошлый раз в статье я попытался перевзвесить на важность синапсов и получилось менее информативно.
В этот раз вооружённый новыми знаниями попытаюсь с помощью t-SNE развернуть многомерное пространство в такую проекцию, в которой всё может быть лучше.
t-SNE
%%time
import sklearn.manifold as manifold
tsne = manifold.TSNE(random_state=19)
tsne_representation = tsne.fit_transform(history)
plt.plot(tsne_representation[:, 0], tsne_representation[:, 1])
plt.savefig("images/pic6.png", format = 'png')
plt.show();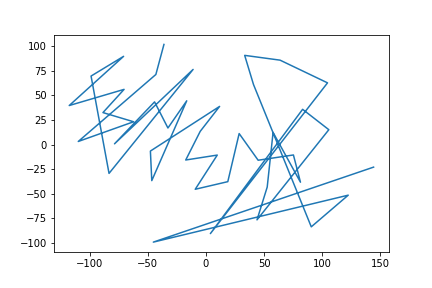
t-Sne похоже развернул пространство так, что начисто съел масштаб изменений по тем фичам, которые быстро перестали меняться, чем сделал картинку совершенно неинформативной. Вывод — не пытайтесь подсовывать алгоритмы в места для них не предназначенные.:\
Дальше можно не читать
Я ещё попытался сделать инъекцию внутрь tsne чтобы визуализировать промежуточные состояния оптимизации, в надежде, что получится красота. но получилась не красота, фигня какая-то. Если интересно — посмотрите как это сделать. В интернете валяется куча примеров кода такой инъекии но простым копированием они не ра ботают, потому что подменяют содержащуюся в sklearn.manifold.t_sne внутреннюю функцию _gradient_descent, а она в зависимости от версии может сильно отличаться как по сигнатуре так и по обращению с внутренними переменными. Так что просто находи у себя исходники выковыриваем оттуда вашу версию функции и вставляем в неё всего одну строчку складывающую промежуточные дампы в вашу какую-то вашу переменную:
positions.append(p.copy()) # We save the current position.
А потом типа красиво визуализируем то что получается в результате:
Код инъекции
from time import time
from scipy import linalg
# This list will contain the positions of the map points at every iteration.
positions = []
def _gradient_descent(objective, p0, it, n_iter,
n_iter_check=1, n_iter_without_progress=300,
momentum=0.8, learning_rate=200.0, min_gain=0.01,
min_grad_norm=1e-7, verbose=0, args=None, kwargs=None):
# The documentation of this function can be found in scikit-learn's code.
if args is None:
args = []
if kwargs is None:
kwargs = {}
p = p0.copy().ravel()
update = np.zeros_like(p)
gains = np.ones_like(p)
error = np.finfo(np.float).max
best_error = np.finfo(np.float).max
best_iter = i = it
tic = time()
for i in range(it, n_iter):
positions.append(p.copy()) # We save the current position.
check_convergence = (i + 1) % n_iter_check == 0
# only compute the error when needed
kwargs['compute_error'] = check_convergence or i == n_iter - 1
error, grad = objective(p, *args, **kwargs)
grad_norm = linalg.norm(grad)
inc = update * grad < 0.0
dec = np.invert(inc)
gains[inc] += 0.2
gains[dec] *= 0.8
np.clip(gains, min_gain, np.inf, out=gains)
grad *= gains
update = momentum * update - learning_rate * grad
p += update
if check_convergence:
toc = time()
duration = toc - tic
tic = toc
if verbose >= 2:
print("[t-SNE] Iteration %d: error = %.7f,"
" gradient norm = %.7f"
" (%s iterations in %0.3fs)"
% (i + 1, error, grad_norm, n_iter_check, duration))
if error < best_error:
best_error = error
best_iter = i
elif i - best_iter > n_iter_without_progress:
if verbose >= 2:
print("[t-SNE] Iteration %d: did not make any progress "
"during the last %d episodes. Finished."
% (i + 1, n_iter_without_progress))
break
if grad_norm <= min_grad_norm:
if verbose >= 2:
print("[t-SNE] Iteration %d: gradient norm %f. Finished."
% (i + 1, grad_norm))
break
return p, error, i
manifold.t_sne._gradient_descent = _gradient_descentПрименяем ''исправленный'' t-SNE
tsne_representation = manifold.TSNE(random_state=17).fit_transform(history)
X_iter = np.dstack(position.reshape(-1, 2) for position in positions)
position_reshape = [position.reshape(-1, 2) for position in positions]
print(position_reshape[0].shape)
print('[0] min', position_reshape[0][:,0].min(),'max', position_reshape[0][:,0].max())
print('[1] min', position_reshape[1][:,0].min(),'max', position_reshape[1][:,0].max())
print('[2] min', position_reshape[2][:,0].min(),'max', position_reshape[2][:,0].max())
(41, 2)
[0] min -0.00018188123 max 0.00027207955
[1] min -0.05136269 max 0.032607622
[2] min -4.392309 max 7.9074526
Значения пляшут в очень широких пределах, поэтому прежде чем их рисовать отмасштабирую их. На циклах всё это делается капец медленно. :(
Масштабирую
%%time
from sklearn.preprocessing import MinMaxScaler
minMaxScaler = MinMaxScaler()
minMaxScaler.fit_transform(position_reshape[0])
position_reshape = [minMaxScaler.fit_transform(frame) for frame in position_reshape]
position_reshape[0].min(), position_reshape[0].max()Анимирую
%%time
from matplotlib.animation import FuncAnimation, PillowWriter
#plt.style.use('seaborn-pastel')
fig = plt.figure()
ax = plt.axes(xlim=(0, 1), ylim=(0, 1))
line, = ax.plot([], [], lw=3)
def init():
line.set_data([], [])
return line,
def animate(i):
x = position_reshape[i][:,0]
y = position_reshape[i][:,1]
line.set_data(x, y)
return line,
anim = FuncAnimation(fig, animate, init_func=init, frames=36, interval=20, blit=True, repeat_delay = 1000)
anim.save('images/animate_tsne_learning.gif', writer=PillowWriter(fps=5))
Поучительно в плане навыков, но абсолютно бесполезно в данной задаче и некрасиво.
На этом я прощаюсь с вами. Надеюсь идея, что даже из knn можно нацедить чего-то нового и интересного, а также кусочки кода, помогут вам также как мне поразвлекаться с данными на этом интеллектуальном пиру во время чумы.


S_A
Вы практически переизобрели metric learning.
http://contrib.scikit-learn.org/metric-learn/introduction.html
И у дерева и knn есть серьёзное отличие: параметрический или нет, метод.
Входная концепция, масштабировать по важности дерева мне понравилась, не делал так :)
kraidiky Автор
Главное, что взять от дерева важности очень быстро получается. Простое дерево учится за считанные миллисекунды.