В предыдущей публикации Алгоритм нечеткого поиска TextRadar. Основные подходы (ч. 1) рассмотрены основные подходы. При решении практических задач были выявлены ситуации, когда использование только базовой методики не обеспечивает требуемого качества поиска. В результате были созданы дополнения (опции алгоритма), о которых и пойдет речь.
Пусть строка поиска ABCD, а строка данных — ABCE DFG.
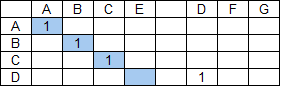
Применение базового алгоритма даст следующий результат:

При возникновении подобных коллизий лишние группы удаляются. Выбор групп для удаления — это отдельный, комплексный вопрос. В результате должны остаться наиболее значимые группы. В случае приведенного примера ответ очевиден — удалить следует наименьшую из групп.

Рассмотрим пример поиска строки ABC в строке XYZAB.

Базовый алгоритм выдаст следующее:

Как правило такой результат не имеет никакой практической ценности и должен быть отброшен.
В случае поиска в строке ABCDEF слова ABXYZ

получим:

Этот результат тоже не представляет ценности и должен быть отброшен.
Даны строка поиска ABCXEF и строка данных ABCEF ABCDEF.

С точки зрения базового алгоритма оба слова строки данных равнозначны, но приоритет будет иметь первое из них (если при прочих равных выбирается первое встретившееся слово) и тогда результат поиска будет следующим:

Если ввести понятие надгруппы как объединения групп слова, расположенных на одной диагонали (или сдвиге, см. предыдущую публикацию, где рассмотрены основы алгоритма) и повысить приоритет входящих в надгруппы групп через параметр размер надгруппы, вычисляемый для каждой из групп и принять при этом, что если группа не входит в надгруппу, то размер надгруппы для нее будет равен размеру самой группы — для нашего примера получим следующий результат:

При поиске фразы, содержащей длинное и короткое слово, найденные фрагменты длинного слова могут «затенять» фрагменты короткого. Это связано с использованием квадратичной функции при расчете коэффициента релевантности.

При этом, с точки зрения качества поиска, более длинное слово не всегда является и более значимым.
Рассмотрим пример. Пусть нужно найти строку ABCDEFG XYZ в тексте, состоящем из двух страниц:
1. ABCDEFG… QWE


2. ABCDEFO… XYZ


Числитель коэффициента состава групп (знаменатель не оказывает качественного влияния на результат, см. формулу выше) для первой страницы составит 49, для второй — 36 + 9 = 45. То есть, если опустить влияние на результат коэффициента протяженности, то результат поиска на первой странице будет иметь бОльшую релевантность, что не соответствует ожиданиям — в ряде случаев результат поиска на странице 2 будет являться более ценным.
Одним из путей решения может быть ввод ограничения на максимальную длину групп. В нашем примере, если максимальную длину групп ограничить к примеру значением 6, то получим для первой страницы 36, для второй — 45, что обеспечит ожидаемый нами результат — релевантность второй страницы будет выше, чем первой.
Еще один путь разрешения проблемы несоответствия значимости слов поисковой фразы в общем результате от их длины — расчет релевантности поисковой фразы как среднего от релевантностей входящих в нее слов, вычисленных независимо. Но здесь возникает обратная проблема — необходимости уменьшения значимости коротких слов, которую можно решать аналогичным образом — установкой порогового значения на длину участвующих в формировании общей релевантности слов, но уже на минимальное значение.
Как следует из постановки, задача состоит в поиске наиболее релевантного строке поиска набора фрагментов, следовательно сам факт многократного повторения искомых фрагментов в тексте не влияет на результат — в качестве результата поиска будет использован первый подходящий фрагмент, остальные отбрасываются в процессе обработки. Рассмотрим пример поиска строки ABC в строке ABCD ABCE ABCF ABCG.

Применение базового алгоритма даст такой результат:

С точки зрения поиска наиболее релевантной страницы это правильно, но при формировании детального представления результатов поиска необходимо найти и выделить все подходящие фрагменты. Для этого можно использовать многократное повторение процедуры поиска по отображаемой странице с последовательным выключением найденных на предыдущих итерациях фрагментов. В нашем примере это позволит найти все подходящие вхождения искомой строки.

Обработка данных «на лету» предъявляет определенные требования к скорости — поиск не должен происходить слишком долго.
Ограничение минимального размера обрабатываемых групп, отключение опций поиска
Для повышения скорости поиска можно ограничить минимальную длину обрабатываемых групп.
На практике применяется следующих подход — сначала делается первый «грубый» проход с ограничением на минимальный размер групп и отключением некоторых опций всего массива данных поиска и выявление первой порции данных (размер оптимальной порции данных определяется из контекста решаемой задачи), а затем второй, более тщательный обход только страниц этой порции, уже без ограничения на размер групп и с включением всех необходимых опций.
Параллельная обработка данных
Еще одной возможностью повышения скорости поиска является параллельная обработка данных. В результате, при большом размере базы поиска, приемлемого общего времени обработки можно достичь увеличением количества параллельных процессов, что естественно потребует наращивания мощности оборудования.
Применение описанных подходов позволило существенно повысить качество поиска, снизить зависимость его результатов от различного рода опечаток — лишние, пропущенные символы, перестановки и т.д., причем, что существенно, неважно где находятся эти опечатки — в самой строке поиска или в тексте, в котором осуществляется поиск.
Результаты применения описанных подходов можно увидеть на демо-стенде, развернутом на сайте textradar.ru. На примере поиска в тексте романа Л.Н. Толстого «Война и мир» можно сравнить результаты поиска с использованием базового и расширенного вариантов алгоритма.

Скачать или посмотреть демо-проект с расширенной функциональностью (C# ASP.NET MVC) можно здесь.
Фрагменты одного слова строки поиска расположены в нескольких словах строки данных
Пусть строка поиска ABCD, а строка данных — ABCE DFG.

Применение базового алгоритма даст следующий результат:

При возникновении подобных коллизий лишние группы удаляются. Выбор групп для удаления — это отдельный, комплексный вопрос. В результате должны остаться наиболее значимые группы. В случае приведенного примера ответ очевиден — удалить следует наименьшую из групп.

Начальный фрагмент слова строки поиска расположен внутри слова строки данных
Рассмотрим пример поиска строки ABC в строке XYZAB.

Базовый алгоритм выдаст следующее:

Как правило такой результат не имеет никакой практической ценности и должен быть отброшен.
Недостаточное покрытие слова строки данных найденными фрагментами
В случае поиска в строке ABCDEF слова ABXYZ

получим:

Этот результат тоже не представляет ценности и должен быть отброшен.
Надгруппы
Даны строка поиска ABCXEF и строка данных ABCEF ABCDEF.

С точки зрения базового алгоритма оба слова строки данных равнозначны, но приоритет будет иметь первое из них (если при прочих равных выбирается первое встретившееся слово) и тогда результат поиска будет следующим:

Если ввести понятие надгруппы как объединения групп слова, расположенных на одной диагонали (или сдвиге, см. предыдущую публикацию, где рассмотрены основы алгоритма) и повысить приоритет входящих в надгруппы групп через параметр размер надгруппы, вычисляемый для каждой из групп и принять при этом, что если группа не входит в надгруппу, то размер надгруппы для нее будет равен размеру самой группы — для нашего примера получим следующий результат:

Завышенная значимость длинных слов
При поиске фразы, содержащей длинное и короткое слово, найденные фрагменты длинного слова могут «затенять» фрагменты короткого. Это связано с использованием квадратичной функции при расчете коэффициента релевантности.

При этом, с точки зрения качества поиска, более длинное слово не всегда является и более значимым.
Рассмотрим пример. Пусть нужно найти строку ABCDEFG XYZ в тексте, состоящем из двух страниц:
1. ABCDEFG… QWE


2. ABCDEFO… XYZ


Числитель коэффициента состава групп (знаменатель не оказывает качественного влияния на результат, см. формулу выше) для первой страницы составит 49, для второй — 36 + 9 = 45. То есть, если опустить влияние на результат коэффициента протяженности, то результат поиска на первой странице будет иметь бОльшую релевантность, что не соответствует ожиданиям — в ряде случаев результат поиска на странице 2 будет являться более ценным.
Одним из путей решения может быть ввод ограничения на максимальную длину групп. В нашем примере, если максимальную длину групп ограничить к примеру значением 6, то получим для первой страницы 36, для второй — 45, что обеспечит ожидаемый нами результат — релевантность второй страницы будет выше, чем первой.
Еще один путь разрешения проблемы несоответствия значимости слов поисковой фразы в общем результате от их длины — расчет релевантности поисковой фразы как среднего от релевантностей входящих в нее слов, вычисленных независимо. Но здесь возникает обратная проблема — необходимости уменьшения значимости коротких слов, которую можно решать аналогичным образом — установкой порогового значения на длину участвующих в формировании общей релевантности слов, но уже на минимальное значение.
Многократные повторения искомых фрагментов
Как следует из постановки, задача состоит в поиске наиболее релевантного строке поиска набора фрагментов, следовательно сам факт многократного повторения искомых фрагментов в тексте не влияет на результат — в качестве результата поиска будет использован первый подходящий фрагмент, остальные отбрасываются в процессе обработки. Рассмотрим пример поиска строки ABC в строке ABCD ABCE ABCF ABCG.

Применение базового алгоритма даст такой результат:

С точки зрения поиска наиболее релевантной страницы это правильно, но при формировании детального представления результатов поиска необходимо найти и выделить все подходящие фрагменты. Для этого можно использовать многократное повторение процедуры поиска по отображаемой странице с последовательным выключением найденных на предыдущих итерациях фрагментов. В нашем примере это позволит найти все подходящие вхождения искомой строки.

Скорость обработки данных
Обработка данных «на лету» предъявляет определенные требования к скорости — поиск не должен происходить слишком долго.
Ограничение минимального размера обрабатываемых групп, отключение опций поиска
Для повышения скорости поиска можно ограничить минимальную длину обрабатываемых групп.
На практике применяется следующих подход — сначала делается первый «грубый» проход с ограничением на минимальный размер групп и отключением некоторых опций всего массива данных поиска и выявление первой порции данных (размер оптимальной порции данных определяется из контекста решаемой задачи), а затем второй, более тщательный обход только страниц этой порции, уже без ограничения на размер групп и с включением всех необходимых опций.
Параллельная обработка данных
Еще одной возможностью повышения скорости поиска является параллельная обработка данных. В результате, при большом размере базы поиска, приемлемого общего времени обработки можно достичь увеличением количества параллельных процессов, что естественно потребует наращивания мощности оборудования.
Результаты
Применение описанных подходов позволило существенно повысить качество поиска, снизить зависимость его результатов от различного рода опечаток — лишние, пропущенные символы, перестановки и т.д., причем, что существенно, неважно где находятся эти опечатки — в самой строке поиска или в тексте, в котором осуществляется поиск.
Результаты применения описанных подходов можно увидеть на демо-стенде, развернутом на сайте textradar.ru. На примере поиска в тексте романа Л.Н. Толстого «Война и мир» можно сравнить результаты поиска с использованием базового и расширенного вариантов алгоритма.

Скачать или посмотреть демо-проект с расширенной функциональностью (C# ASP.NET MVC) можно здесь.


teoadal
Спасибо за интересную и познавательную статью!
Скажите, а код, который сейчас выложен в GitHub (ссылка и код, который сейчас вы предлагаете скачать с Я.Диска в качестве архива — это одинаковый код? Очень не удобно скачивать архивы, но посмотреть код было бы очень интересно.
TSSV Автор
Спасибо за отзыв! Это по сути две версии одного и того-же кода. На GitHub — только базовая функциональность (ссылка на нее приведена в первой части), образованная удалением «лишнего» из полной версии, а в архиве — базовая плюс описанные опции (но не только), образующие т.н. расширенную версию (ссылка приведена в данной публикации). Так сделано потому, что, с одной стороны, базовая версия появилась раньше, а с другой — расширенная версия может показаться сложной для восприятия и тогда имеет смысл смотреть эти вещи отдельно. По поводу скачивания архива — я постараюсь это учесть и выложить расширенный вариант и на GitHub тоже.
TSSV Автор
github.com/tsaregorodtseff/TextRadarExtended