Алгоритм нечеткого поиска TextRadar — основные подходы
В отличие от нечеткого сравнения строк, когда обе сравниваемых строки равнозначны, в задаче нечеткого поиска выделяются строка поиска и строка данных, а определить необходимо не степень похожести двух строк, а степень присутствия строки поиска в строке данных.
Постановка задачи
Даны строка данных и строка поиска как произвольные наборы символов, состоящих из слов – групп символов, разделенных пробелами.
Требуется найти в строке данных наиболее близкий к строке поиска по составу и взаимному расположения символов набор фрагментов.
Для оценки качества результата поиска вычислить коэффициент, значение которого должно лежать в диапазоне от 0 до 1, где 0 должен соответствовать полному отсутствию символов строки поиска в строке данных, а 1 – наличию строки поиска в строке данных в неискаженном виде.
Поиск должен осуществляться путем посимвольного анализа исходных строк, с учетом взаимного расположения символов и слов в строках, но без учета синтаксиса и морфологии языка.
Описание алгоритма
Поиск осуществляется в несколько этапов.
Построение матрицы совпадений
Матрица совпадений (M) представляет собой двумерную матрицу, количество столбцов которой соответствует длине строки данных, а количество строк – длине строки поиска. Элементы матрицы совпадений принимают значения 0 или 1 в зависимости от того, совпадают или нет соответствующие символы строк за исключением пробелов (разделителей слов).
Матрица совпадений для строки данных «ABCD EF» и строки поиска «ABC» имеет вид:
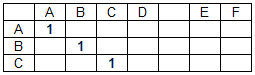
Элемент матрицы совпадений m(i, j) = 1, если d(i) = s(j), где D – массив символов строки данных, S – массив символов строки поиска, i – номер столбца матрицы совпадений M (номер символа строки данных), j – номер строки матрицы совпадений (номер символа в строке поиска). В остальных случаях m(i,j) = 0. Совпадения разделителей слов (в нашем случае это пробелы) не учитывается, то есть: m(i,j) = 0, если d(i) = s(j) = ‘ ‘.
Диагонали матрицы совпадений
Элементы матрицы совпадений M образуют диагонали. Элементы матрицы находятся на одной диагонали, если их индексы i и j одновременно различаются на +1 или на – 1.

Диагонали соответствуют положениям строки поиска в последовательности сдвигов вдоль строки данных.

Элементы одной из диагоналей и соответствующий ей сдвиг на рисунке выше выделены синим.
Идея использования последовательности сдвигов строк друг относительно друга в задаче нечеткого поиска восходит к хорошо известной методике обнаружения радиолокационных сигналов на фоне помех, которая предполагает вычисление взаимной корреляционной функции радиосигналов. Взаимнокорреляционная функция определяет степень схожести копий двух различных сигналов v(t) и u(t), сдвинутых на время ? друг относительно друга и определяется как интеграл:
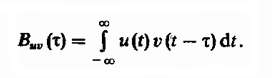
Общее количество диагоналей рассчитывается по формуле:

Длины диагоналей равны длине строки поиска.
Группы совпадений
Единицы, следующие подряд в диагоналях матрицы совпадений, образуют группы совпадений. Ниже представлены группы совпадений для строки данных «ABCD DEF JH» и строки поиска «ABC DE J» — 4 группы, находящиеся на разных диагоналях.

Матрицы проекций
Диагонали матрицы совпадений и содержащиеся в них группы совпадений отображаются на соответствующие участки строки поиска и строки данных, образуя две матрицы проекций – на строку поиска и на строку данных соответственно. Для нашего примера матрицы проекций будут выглядеть следующим образом:
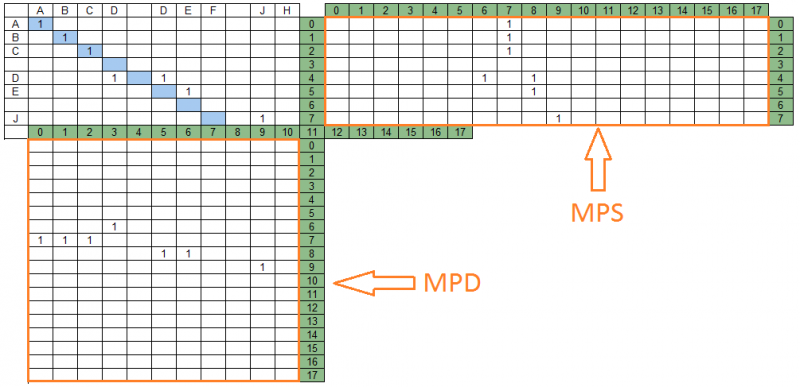
На приведенном рисунке, справа от матрицы совпадений находится матрица проекций на строку поиска — MPS, снизу – матрица проекций на строку данных MPD. Количество столбцов MPS равно количеству строк MPD и равно числу диагоналей матрицы совпадений – в нашем примере их 18.
Поиск результирующего набора групп
Для решения задачи необходимо найти такой набор групп, который наиболее полно «накроет» строку поиска, при этом наименее фрагментировано (максимально крупными частями), без взаимных пересечений в матрицах проекций и отображение которого на строку данных будет наиболее близко к «оригиналу» — строке поиска.
Пересечение групп в матрице проекций
В нашем примере есть группы, пересекающиеся в матрице MPS – на рисунке ниже они выделены красным. При этом в матрице MPD эти же группы не пересекаются, на рисунке они выделены зеленым.
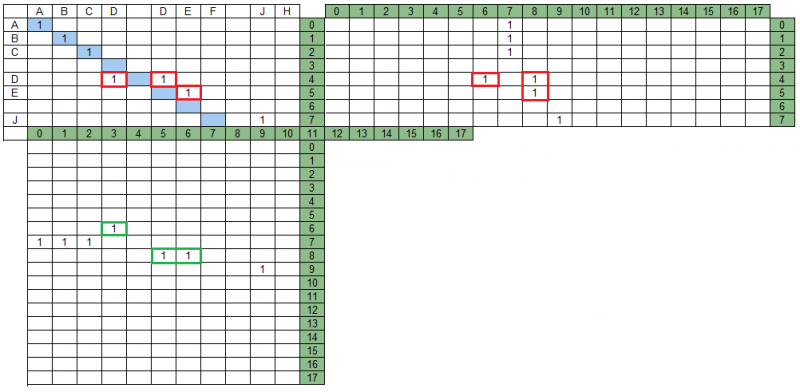
Поиск результирующего набора групп подразумевает, что в него войдут не все группы и что часть из оставшихся групп может быть модифицирована (усечена) при анализе взаимных пересечений групп в проекциях.
Поиск результирующего набора может быть осуществлен путем обхода в «бесконечном» цикле (количество итераций цикла не превысит количества групп) таблицы всех групп, в которую изначально помещаются группы матрицы совпадений, на каждой итерации которого будут осуществляться следующие действия:
- Выбор наилучшей по определенным (зависящим от контекста решаемой задачи) параметрам — в самом простом случае это может быть выбор первой попавшейся группы наибольшего размера;
- Помещение лучшей группы в таблицу групп результата и удаление ее из таблицы всех групп (обход строк которой производится);
- Удаление (или усечение) из таблицы групп пересекающихся с выбранной наилучшей группой в матрицах проекций групп.
Оптимальный набор групп для нашего примера представлен на рисунке ниже — группы набора выделены оранжевым.

Удаленная в процессе обработки пересечений (пересекающаяся в матрице MPS с наилучшей группой второй итерации) группа выделена красным.
Результат поиска в строке данных будет выглядеть так:

Вычисление коэффициента
Для количественной оценки результатов поиска сопоставляются длины найденных групп с длинами слов строки поиска (оценка состава групп), а также общая длина строки поиска с протяженностью найденных групп в строке данных. При этом предполагается, что значимость оценки состава найденных групп выше значимости оценки протяженности в строке данных, что учтено в весовых коэффициентах формулы расчета итогового коэффициента:

Где коэффициент состава групп рассчитывается как отношение суммы квадратов длин найденных групп к сумме квадратов длин слов строки поиска:

Коэффициент протяженности – как отношение длины строки поиска к общей протяженности найденных групп на строке данных. В случае, если полученное таким образом значение больше 1, берется его обратная величина:

Для нашего примера:

Оценка объема вычислений
Наиболее ресурсоемкими являются операции:
- определение матрицы совпадений M — количество элементов матрицы определяется как произведение длины строки поиска на длину строки данных: Lп * Lд;
- определение матриц проекций на строки данных и поиска — количество элементов матриц составит для MPS: (Lп + Lд – 1) * Lп, для MPD: (Lп + Lд – 1) * Lд;
- формирование таблицы всех групп — количество групп не превысит величины Lп * Lд / 2;
- поиск результирующего набора групп — количество итераций цикла не превысит исходного количества групп, то есть Lп * Lд / 2.
Таким образом, общий объем вычислений будет кратен произведению длины строки поиска на длину строки данных:

Линейность объема вычислений относительно размера исходных данных является важным аргументом в пользу практического применения алгоритма.
Нелинейность
Стоит отметить, что линейность обусловлена упрощенной процедурой поиска результирующего набора групп. В общем случае, если рассматривать все возможные варианты размещений групп на строке данных с учетом возможных вариантов обработки пересечений и осуществлять выбор наилучшего набора групп из множества возможных, а не выбор одной группы на каждой итерации цикла, то объем вычислений перестанет быть линейным по отношению к размеру исходных данных. Нелинейная зависимость объема вычислений от размера исходных данных сильно ограничивает возможности практического применения.
Находим баланс
Для обеспечения оптимального баланса между качеством поиска и потребностью в ресурсах, важно правильно выбрать методику поиска результирующего набора групп, что как правило удается сделать, используя особенности контекста решаемой задачи.
На сайте textradar.ru развернут демо-стенд, на котором можно протестировать работу алгоритма.
Комментарии (16)

belomor77
06.11.2019 15:21Напоминает метод N-грамм

TSSV Автор
06.11.2019 15:37Согласен, но я отталкивался от теоретических основ радиолокации и немного «шел своим путем». Фактически числитель формулы вычисления коэффициента состава групп

и есть вычисление ВКФ
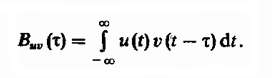
только применительно к строкам. Группы пришлось ввести для повышения влияния на результат подряд совпадающих символов, что достигнуто возведением размеров групп в квадрат. Потом обнаружилась проблема пересечений, сначала в одной проекции, затем во второй.
belomor77
06.11.2019 15:49Скачал с Инфостарта Вашу обработку, попробую переделать для поиска дублей номенклатуры. Сам делал поиск методом N-грамм на встроенном языке 1С, но чуть-чуть не дошел до финала

TSSV Автор
06.11.2019 20:22Надеюсь дойдете еще. Версия этого алгоритма на языке 1С у меня тоже есть (изначально я на 1С алгоритм разрабатываю, потом переношу на C#), кстати время выполнения очень сильно различается. За то время, которое 1С тратит на вычисления только по одной странице текста, C# успевает обработать все 1490. На Инфостарте предыдущая версия алгоритма, на демо-стенде более продвинутая, но подход тот-же. Надеюсь пригодится. Если доберусь до ее переделки, как увидите на сайте новую версию, напишите — пришлю. Но не обещаю, что доберусь в ближайшее время.

DjSens
06.11.2019 22:49у меня тоже был нечёткий поиск в 3д карте города — поиск заведений и магазинов по адресу, описанию и отзывам (одновременно), очень хорошо всё находилось. Алгоритм был простой — строку поиска разбиваем на слова и потом ищем каждое искомое слово в строке данных, если слово найдено, то вес результата увеличиваем на длину этого слова. Потом сортируем результаты по весам. Если в базе про одно здание написано «проспект Ленина дом 123 магазин Хозяин лаки краски инструменты и т.п.» то для поиска достаточно набрать в любом порядке слова такие например: «краски лаки Ленина». Хотел улучшить чтоб слова с опечатками искались, но не понадобилось, сначала и так было хорошо, а потом проект закрыл т.к. пришёл 2GIS в наш городок. С опечатками можно искать просто по наличию нужных букв в слове (это увеличивает вес результата), а если ещё и порядок букв совпадает — то вес каждой буквы можно умножать на 2


Sovetnikov
Демо стенд быстроработает и на первый взгляд хорошо находит то что искали.
А опечатки вида перестановки букв местами не будет поддерживать?
Есть ли реализация которой уже можно воспользоваться?
Сколько занимают подготовленные матрицы?
TSSV Автор
Спасибо! Реализовано на C#, использован многопоточный цикл (Parallel.For). Хостинг – самый дешевый .NET на REG.RU, плюс сам поиск (по Войне и миру) организован в 2 этапа — сначала грубая оценка всего массива строк (1490 страниц) с ограничением по длине групп больше или равно 2, затем уточненная для первых 100 элементов грубой оценки с формированием данных для отображения, далее результаты отсекаются по порогу коэффициента > 0.5. И еще несколько моментов, позволяющих ускорить расчет. Есть возможности еще ускорить – не стал этого делать, чтобы не потерять «наглядность» алгоритма.
Если не сложно, просьба прислать пример. Если я правильно понял, то видимо вопрос в отображении результатов. Перестановки букв находят отражение в коэффициенте. То есть в визуальном отображении результатов поиска рядом стоящие идущие подряд в строке поиска и переставленные местами символы строки данных будут отображаться одинаково, но коэффициент будет разным. Например «абв» с «абв» даст коэффициент 1, а «абв» и «вба» только 0.61. Но с отображением можно поработать, как и самим поиском – по конкретным кейсам.
Сейчас алгоритм стенда не содержит никаких изощренных особенностей и довольно легок для восприятия. Все практически как в описании, только немного более хитрый выбор лучшей группы и обработки пересечений.
реализация только та, что на демо-стенде (на C#, MVC).
Если я правильно понял вопрос. Никакой предварительной индексации текста не производится, все вычисления происходят «как в первый раз», в оперативной памяти находится только массив строк текста «Войны и мира» — не стал связываться с БД.
Sovetnikov
Пример с опечаткой поиск по «вйона» вместо «война».
С пропуском букв кстати хорошо работает, поиск по «голву» вместо «голову».
Я подумал, что матрицы предварительно сгенерированные берутся из БД, класно что на лету всё, т.е. ещё быстрее может всё работать?
C# не наша платформа, только если в виде сервиса с API на .NET Core в Docker, или консольной утилиты смогли бы к себе внедрить. На Python портировать смысла наверное нет, производительность упадёт.
А сравнивали с другими реализациями нечеткого поиска? Elastic и т.п.? По скорости и качеству.
Мы просто пользуемся в паре мест github.com/seatgeek/fuzzywuzzy (на левенштейне работает) для нечеткого поиска по небольшому сету строк (до 2000 строк, длина не более 100 символов), но он работает очень уж медленно.
TSSV Автор
Для меня этот проект скорее хобби и возможность поработать на других платформах, так как я на 1С специализируюсь (так исторически сложилось). Но можно решить я думаю. Есть старый вариант dll на С++, правда там без многопоточности.
Mingun
Еще пример плохого поиска — "крове" (опечатка для поиска "кроме"). Не находит не одного релевантного совпадения в первой сотне. Если исправить опечатку (т.е. искать "кроме"), вся первая сотня содержит это слово.
Алгоритм с отсечением единичных букв для "крове" вообще находит только одну страницу и подсвечивает "кр" в "крикнул".
Кстати, вот не согласен, что в первую очередь важна скорость. В первую очередь важен результат. Лучше искать чуть медленнее, но более релевантно, особенно по "плохим" словам, чем совсем их отсекать.
TSSV Автор
За примеры спасибо!
На сайте tools41.ru кстати есть встроенный поиск по сайту от Яндекса, вот ссылка на него: tools41.ru/Home/Pagination?Length=0 Поиск установлен давно, уже год примерно.
Яндекс по умолчанию опечатки исправляет еще до старта поиска — думаю в этом есть смысл. По «крове» и по «вйона» тоже будет пусто (в кавычках если набирать, чтобы не исправил).
По поводу скорости, я согласен с Вами — приоритетно качество.
Имелось ввиду, что, например, зная эпизод сцены вызова Долохова Пьером на дуэль, и что в тексте вызов происходит на странице 378, я ввожу строку «пьер вызывает долохова на дуэль» — результат и в быстрой и в медленной версии меня устраивает, искомая страница на 2-м месте, остальные значимые страницы эпизода тоже в первой десятке. Тогда я предпочту быструю версию. То же самое по другим фрагментам — «вечер у анны павловны шерер», «самоуверенность немца, француза, русского» (интересное рассуждение на странице 782).
В случае опечаток да, медленная версия выигрывает, но тоже не самым лучшим образом.
domix32
Предложил бы посмотреть на fst
Sovetnikov
Надо попробовать, есть Python bindings
TSSV Автор
Поторопился, прошу прощения.
«вйона» и «война», группы «в», «й», «о» и «на». При грубом проходе группы единичной длины игнорируются, поэтому и результат такой плохой, так как остаются только страницы, содержащие «на», а эта группа есть почти везде. Причина в этом и только в этом.
Убрал отсечение групп единичной длины при грубом проходе. Скорость обработки снизилась, но зато качество выше. Но думаю все же в большинстве случаев скорость предпочтительней.
TSSV Автор
На сайте tools41.ru выложил предыдущий, быстрый вариант (с отсечением групп единичной длины), так что теперь можно сравнить результаты.
Sovetnikov
Поиск по фразам тоже приятные результаты выдаёт.