В этой части я расскажу как рассчитывал вероятности обнаружения агентов в ячейках в зависимости от плотности заселения пространства Dракошами. А также о том, как можно наблюдать что Dракоши становятся более сознательными жильцами своей вселенной.
Кто такие Dракоши смотрите в первой части.
1. Зачем нам вероятности?
2. Постановка задачи
3. Подсчет способов расстановки агентов
4. Моделирование вероятностей методом Монте-Карло
5. Что получилось?
Прежде чем начать запускать моделирование надо бы понять, а как мы будем «смотреть» на мир Dракош? Ведь их будут тысячи, каждый будет заниматься своими делами, куда-то идти, что-то кушать и т.д.…
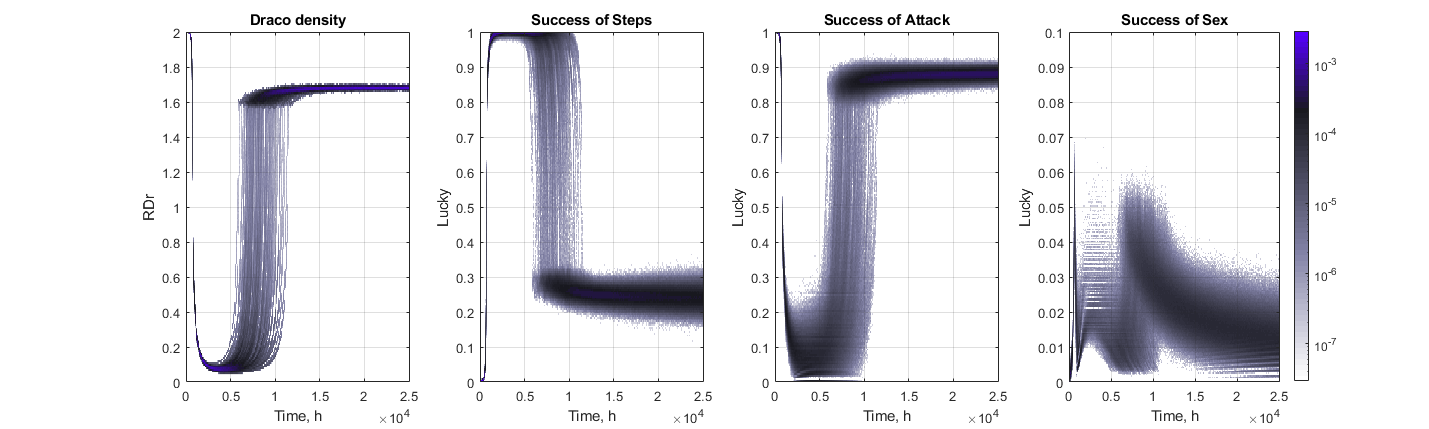
Поэтому в самом начале пришлось задумался о параметрах, которые будут описывать текущее состояние моделируемой системы и показывать динамику происходящих в ней изменений. Получилось всего 24 величины, за которыми интересно проследить, помимо самого пространства с распределением агентов и пищи. Среди этих параметров есть вполне очевидные: количество агентов, количество пищи в пространстве, рождаемость и смертность… Но о них более подробно будет рассказано в третей части. Сейчас же я больше остановлюсь на специальной группе параметров, которые позволят оценить степень «осознанности» действий агентов. Другими словами, отличить случайное поведение от «осознанного».
Напомню, агенты могут совершать шесть разных действий: Pass, Step 1, Step 2, Eat, Attack, Sex. Для каждого из них можно рассчитывать долю агентов, которые его совершает в течении каждого такта времени: , , , , , . Эти шесть параметров позволят понять, что делают Dракоши.
Все действия кроме Pass могут быть успешными или неуспешными, в зависимости от сложившейся ситуации в текущей и в соседних ячейках, а также от желаний соседа по занимаемой ячейке. Для отслеживания успешности используются четыре параметра: , , , . Они показывают какая доля из совершенных действий была успешной. При этом оба действия Step 1 и Step 2 учитываются в одном параметре .
На начальном этапе, когда нейронная сеть агентов еще не обучена, действия агентов будут носить случайный характер. А по мере эволюционного развития, под действием отбора, можно ожидать увеличения степени осознанности и следовательно повышения успешности действий. Но необходимо учесть, что успешность действий зависит так же и от окружающей обстановки.
Так успешность действий Step 1/2 определяется наличием в ячейке, которую агент выбрал для перемещения, свободного места (всего в ячейках есть по два места для агентов). И будет зависеть как от правильности выбора агента, так и от количества агентов в пространстве. Текущее количество агентов удобно отслеживать с помощью параметра – плотность агентов в пространстве, которая равна отношению количества агентов к количеству ячеек в пространстве. Когда агентов в пространстве мало, плотность близка к нулю и вероятность того, что в выбранной агентом ячейке будет свободное место близка к единице. Поэтому несмотря на наличие или отсутствие «осознанности» у агентов при низкой плотности агентов () успешность действий Step 1/2 будет высокой (). По мере увеличения количества агентов вероятность обнаружить в выбранной случайно ячейке свободное место снижается вместе с успешностью , если только выбор ячейки для совершения шага не будет делаться осознано. Когда количество агентов будет близко к максимальной емкости пространства () вероятность найти свободное место станет близкой к нулю (). Можно ввести параметр осознанности действий Step 1/2, который рассчитаем, как разность между текущей успешностью и вероятностью обнаружить свободное место в ячейке :
Здесь – обозначает вероятность присутствия в выбранной ячейке двух агентов.
Таким же образом успешность действий Attack и Sex будет зависеть от вероятности () что агент обнаружит в ячейке, которую он занимает, еще одного агента.
Осознанность совершения атаки можно определить как превышение успешности над вероятностью :
А вот успешность зависит не только от вероятности найти партнера в ячейке, но и от вероятности что партнер тоже совершает в данный момент действие Sex. Но даже если партнер оказался сговорчивым, для успешного полового акта необходимо что бы в окружающем пространстве нашлось место для малыша. Поэтому вероятность случайного успеха будет произведением вероятностей трех независимых событий: – в ячейке есть потенциальный партнер, – партнер так же совершает действие Sex, – в ячейке, которую выбрала мать для размещения ребенка, есть свободное место. Поэтому осознанность брачного поведения предлагаю определить таким образом:
Для вычисления введенных выше индексов осознанности необходимо научится рассчитывать две вероятности: и . Очевидно, что они зависят от плотности агентов в пространстве, а также от равномерности их распределения по пространству. Но для упрощения расчетов в дальнейшем будем предполагать равномерное распределения агентов по пространству. То есть будем считать, что эти вероятности не зависят от положения агента в пространстве.
Сформулируем задачу следующим образом.
Для решения данной задачи я применил два подхода. Первый – это расчет вероятности в классическом ее понимании, как отношение количества различных расстановок агентов, которые благоприятствуют искомому событию, к полному количеству расстановок агентов по ячейкам. Для вычислений воспользовался методом производящих функций.
Во втором подходе использовалось понятие частотной вероятности. Расчеты выполнялись с применением метода Монте-Карло. Вероятно, есть и другие способы вычислить эти вероятности, и возможно даже более простые. Буду благодарен за наводку на таковые.
Предложенный ниже подход к расчету вероятностей позволяет решить поставленную задачу даже в более общей постановке, когда вместимости ячеек различны. Зададим вместимости ячеек пространства в виде последовательности , где – номер ячейки (от до ). Для удобства вычислений перенумеруем ячейки таким образом что бы у выбранной для определения вероятностей ячейки был номер .
Поставленную задачу можно свести к подсчёту количества способов расставить агентов по ячейкам пространства. Тогда вероятность – это отношение количества способов расстановки агентов, при которых в ячейку попадает хотя бы один агент, к полному количеству способов расставить агентов по ячейкам пространства. Для мира Dракош вместимость всех ячеек равна двум. Но при расчете вместимость ячейки принимается , т.к. изначально известно, что в этой ячейке уже есть один агент (см. определение вероятности выше).
Вероятность – это отношение количества способов расстановки агентов, при которых в ячейку попадает предельное для этой ячейки количество агентов – , к полному количеству способов расставить агентов по ячейкам пространства.
Обозначим через количество способов расставить агентов по ячейкам с по первую. Так же для вычислений нам понадобится знать количество свободных мест в ячейках с по первую – :
Рассмотрим процесс, при котором мы последовательно перебираем все ячейки пространства (от до ) и на каждом шаге помещаем в очередную ячейку – некоторое количество агентов – , пока не расставим все неразмещенных агентов или не исчерпаем все ячейки. В ячейку можно поместить от до агентов. Но если агентов осталось меньше максимальной вместимости ячейки, то в текущую ячейку можем поместить не более агентов. Таким образом .
Количество способов заполнить ячейку агентами – это сочетание без повторений из по :
Поместив агентов в ячейку , останется еще агентов для расстановки в ячейки с по . И каждому будет соответствовать способов расстановки оставшихся агентов. Произведение – даёт нам количество способов разместить агентов в ячейке и агентов по остальным ячейкам. Суммируя по всем допустимым значениям , получим искомое количество способов расстановки:
Для того что бы воспользоваться полученной рекуррентной формулой необходимо задать граничные условия:
Теперь можем записать выражения для вероятности :
где – это количество способов расстановки агентов, при которых в ячейку попадает один и более агентов:
Обратите внимание, здесь начинаем суммировать с единицы, т.к. нас интересуют те расстановки, при которых в ячейку попадает хотя бы один агент.
Выражения для вероятности :
где – это количество способов расстановки агентов, при которых в ячейку попадает предельное для этой ячейки количество агентов:
Количество расстановок очень быстро растет и уже для чисел двойной точности не хватит. Даже если воспользоваться пакетами символьных вычислений с произвольной точностью (например, Symbolic Math Toolbox и Variable-precision arithmetic в среде MatLab) останется проблема переполнения стека вызовов рекуррентной функции при больших размерах пространства. Поэтому полученные выше выражения необходимо преобразовать. А еще лучше вывести формулу, с помощью которой сразу вычисляется без необходимости считать предыдущие значения.
Первое что можно сделать это вынести из-под знака суммы .
Но прежде введем обозначение приведенного количества расстановок агентов по ячейкам, которое в раз меньше:
И можем сократить выражения для вероятностей на факториал:
Где
После введения новых обозначения требуется переписать выражения для граничных условий. Для дальнейших выкладок удобнее представить граничные условия в следующем виде:
Полученные выражения для приведенных количеств расстановок смотрятся поинтереснее т.к. коэффициенты в рекуррентной формуле постоянны и не растут со скоростью факториала как в формулах выше. Но все равно быстро и надежно вычислить вероятности при размерах пространства порядка 104 не очень получится.
Следующим шагом предлагаю избавится аж от трех видов выражений для приведенного количества расстановок: , , . Для этого достаточно выразить вероятности через . Тут нам придется вспомнить что вместимость ячеек в мире Dракош везде , кроме выбранной ячейки в которой одно место уже занято и поэтому . Дальнейшие решение поставленной задачи в общей постановке (когда вместимость ячеек произвольна) существенно усложнит выкладки в и так затянувшемся погружении в мир комбинаторики.
Готовые выражения для вероятностей теперь зависят только от приведенного количества способов расстановки агентов одного вида – :
Осталось научится рассчитывать элементы последовательности для произвольно больших значений и . Порывшись в учебниках по комбинаторике я нашёл довольно популярный и мощный метод для решения всяческих комбинаторных вопросов – метод производящих функций.
Хорошим пособием для начинающих комбинаторов по производящим функциям можно назвать учебник Ландо С.К. [3]. Еще один ресурс типа справочник по производящим функциям. И еще вот этот пост на хабре. Но наиболее полезными для меня были видео лекции Игоря Клейна по производящим функциям, выложенные тут.
Но в перечисленных ресурсах в основном речь ведется о производящих функциях для одномерных последовательностей, с одним индексом. А наша последовательность двумерная, с двумя индексами. Производящие функции от двух переменных лишь упоминаются. Поэтому пришлось рискнуть и попробовать вывести производящую функцию для нашей двумерной последовательности на основе одномерных примеров.
Суммируя то, что имеется на данный момент по нашей последовательности приведенных количеств расстановок запишем рекуррентную формулу для совместно с граничными условиями.
Наша последовательность зависит от двух индексов: – количество ячеек в пространстве для расстановки агентов, ; – количество агентов для расстановки в ячейках, . Поэтому и производящая функция ей нужна двумерная – .
Используя специальный технический примем можно из рекуррентного выражения для элементов последовательности получить выражение для производящей функции. У меня получилось вот это:
Теперь дело за малым, разложить полученную производящую функцию в ряд по степеням . Собственно, произвести элементы последовательности:
Теперь все что нам нужно это выделить коэффициент при , это и будет искомое выражение для элемента последовательности :
Для этого необходимо сгруппировать все слагаемые, у которых степень — равна . Пределы суммирования при этом будут следующими: при , ; при , .
В результате получим два выражения, одно для чётного :
и одно для нечетного :
Полученные выражения уже можно попробовать вычислить, но так как биноминальные коэффициенты, которые входят в них, всё же растут довольно быстро, для расчетов необходимо воспользовался инструментами символьных вычислений MatLab.
Метод Монте-Карло или метод статистических испытаний — это большая группа численных методов решения математических задач (причем не только вероятностной природы) при помощи моделирования случайных величин. Один из вариантов метода Монте-Карло предполагает что смоделированная случайная величина с известным распределением (зачастую равномерно распределённая на отрезке 0..1) используется для установления статистических характеристик других случайных величин или для приближённой оценки некоторого значения . Во втором случае придумывается некоторая случайная величина , такая что ее мат. ожидание равно искомой величине . Тогда рассчитав независимых значений случайной величины , , …, определяют величину как среднее арифметическое выборки , …, [2].
Для установления статистических характеристик случайных величин, например, для определения вероятности случайного события , можно реализовать другой вариант метода Монте-Карло. Когда проводится моделирование такой случайной величины , которая равна при реализации случайного события на испытании , или равна если события не наступило. При проведении независимых испытаний частота события , равная , стремится к искомой вероятности по мере роста количества испытаний [3]. Если для моделирования случайной величины в модели полностью или частично воспроизводится изучаемый естественный процесс, то такой подход так же называют – имитационным моделированием.
На сегодня метод имитационного моделирования развился в самостоятельное направление методов исследований. Но для решения поставленной в разделе 2 задачи использовался подход, который с одной стороны является примером реализации методов Монтер-Карло, с другой это пример имитационного моделирования, т.к. использовался «естественный» процесс изменения положения агентов в пространстве.
В рамках метода Монте-Карло поставленная в разделе 2 задача сводится к оценке частоты реализации соответствующих событий. Так вероятность – это частота обнаружения агентами соседей по ячейке. А вероятность – это частота обнаружения ячеек с двумя агентами.
Будем рассматривать процесс заполнения ячеек агентами, так что в одной ячейке может быть не более агентов. На каждом шаге будем пересаживать агентов в новые ячейки, и если при попытке пересадить агента окажется что в выбранной ячейке нет свободного места, то оставляем агента на старом месте.

После каждого этапа пересаживаний будем подсчитывать количество полностью заполненных ячеек (с двумя агентами).
Частота обнаружения ячеек с двумя агентами (вероятность ) это просто:
Можно предложить несколько вариантов реализации этапа пересаживания:
Scenario 1 назван почти полной имитацией процессов в настоящем мире Dракош, так как доля агентов совершающих действия Step 1/2 различна для каждого такта времени и может иметь любое значение а не только 50%. Ниже мы посмотрим, как результаты вычислений зависят от сценария пересаживания агентов.
Процесс начинаем со случайной расстановки агентов по ячейкам. Затем в цикле раз повторяются два этапа:
Возникает вопрос: сколько же раз необходимо повторить цикл? С ростом неопределенность вычислений убывает пропорционально . Т.е. для увеличения точности в 10 раз необходимо увеличить количество испытаний в 100 раз. Метод Монте-Карло похож на натурные физические эксперименты в том плане что точность результатов можно определить только после получения результата эксперимента. Точнее случайную составляющую неопределенности. И так же как в натурном эксперименте ею можно управлять изменяя количество измерений.
На графике ниже показана зависимость вероятности для и () от количества испытаний. Для каждой точки показаны планки неопределенности, которая рассчитывалась на основе стандартного отклонения полученных выборок и коэффициента охвата (надежность 99.7%).
Горизонтальной чертой отмечено точное значение, рассчитанное способом, описанным в разделе 3.
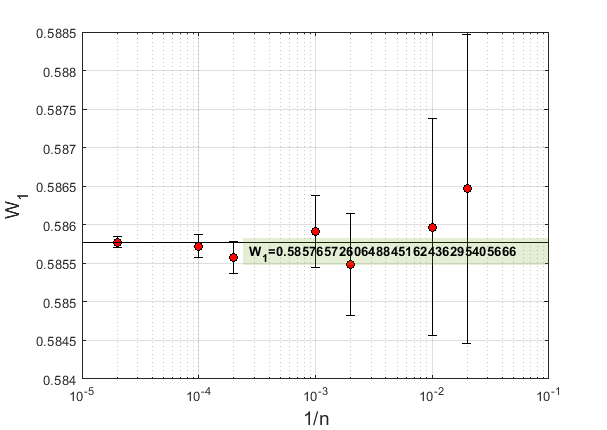
По результатам расчетов получены следующие значения неопределенности (надежность 99.7%):
Т.к. время вычислений растет пропорционально количеству испытаний (для составило около 6.5 часов), а желания сильно оптимизировать код у меня не было, решено было для последующих экспериментов использовать по 1000 испытаний.
Давайте посмотрим, как зависит рассчитываемые значения вероятностей от используемого сценария пересаживания агентов. Ниже показаны результаты вычислений для разных сценариев, при и () и количестве испытаний по .

Как можно видеть отличия между рассчитанными значениями вероятностей с использованием разных сценариев намного меньше неопределенности этих результатов. Это позволяет заключить что более точная имитации мира Dракош привела бы к такому же результату. Поэтому не зачем тратить время.
На графике ниже показаны зависимость вероятностей и от плотности агентов в пространстве. Синяя и красная области — это массивы данных, насчитанные методом Монте-Карло (по 1000 итераций для каждого значения ). Черные линии — это точные значения, вычисленные методом, описанным в разделе 3.

Совпадение результатов, полученных разными методами, позволяет надеяться, что серьезных ошибок не было допущено.
Теперь можем посмотреть, как выглядит успешность действий Step 1/2, Attack и Sex при полностью случайном (неосознанном) поведении агентов. А точнее на вторые слагаемые в выражениях для индексов осознанности, которые как раз и задают базовый уровень успешности, обусловленный вероятностями обнаружения агентов в пространстве:
Для однозначности примем что частота действия Sex – (т.е. если партнер был замечен в ячейке, то он принимает участие в размножении18+ content).

В дальнейшем мы сравним полученные результаты с успешностью Тупиков (раса агентов без нейронной сети) и полноценных Dракош и посмотрим, как будет расти успешность в результате развития нейронной сети агентов.
Кто такие Dракоши смотрите в первой части.

1. Зачем нам вероятности?
2. Постановка задачи
3. Подсчет способов расстановки агентов
4. Моделирование вероятностей методом Монте-Карло
5. Что получилось?
1. Зачем нам вероятности?
Как уследить за Dракошами
Прежде чем начать запускать моделирование надо бы понять, а как мы будем «смотреть» на мир Dракош? Ведь их будут тысячи, каждый будет заниматься своими делами, куда-то идти, что-то кушать и т.д.…
Поэтому в самом начале пришлось задумался о параметрах, которые будут описывать текущее состояние моделируемой системы и показывать динамику происходящих в ней изменений. Получилось всего 24 величины, за которыми интересно проследить, помимо самого пространства с распределением агентов и пищи. Среди этих параметров есть вполне очевидные: количество агентов, количество пищи в пространстве, рождаемость и смертность… Но о них более подробно будет рассказано в третей части. Сейчас же я больше остановлюсь на специальной группе параметров, которые позволят оценить степень «осознанности» действий агентов. Другими словами, отличить случайное поведение от «осознанного».
Напомню, агенты могут совершать шесть разных действий: Pass, Step 1, Step 2, Eat, Attack, Sex. Для каждого из них можно рассчитывать долю агентов, которые его совершает в течении каждого такта времени: , , , , , . Эти шесть параметров позволят понять, что делают Dракоши.
Все действия кроме Pass могут быть успешными или неуспешными, в зависимости от сложившейся ситуации в текущей и в соседних ячейках, а также от желаний соседа по занимаемой ячейке. Для отслеживания успешности используются четыре параметра: , , , . Они показывают какая доля из совершенных действий была успешной. При этом оба действия Step 1 и Step 2 учитываются в одном параметре .
Индексы осознанности или зачем нам вероятности
На начальном этапе, когда нейронная сеть агентов еще не обучена, действия агентов будут носить случайный характер. А по мере эволюционного развития, под действием отбора, можно ожидать увеличения степени осознанности и следовательно повышения успешности действий. Но необходимо учесть, что успешность действий зависит так же и от окружающей обстановки.
Так успешность действий Step 1/2 определяется наличием в ячейке, которую агент выбрал для перемещения, свободного места (всего в ячейках есть по два места для агентов). И будет зависеть как от правильности выбора агента, так и от количества агентов в пространстве. Текущее количество агентов удобно отслеживать с помощью параметра – плотность агентов в пространстве, которая равна отношению количества агентов к количеству ячеек в пространстве. Когда агентов в пространстве мало, плотность близка к нулю и вероятность того, что в выбранной агентом ячейке будет свободное место близка к единице. Поэтому несмотря на наличие или отсутствие «осознанности» у агентов при низкой плотности агентов () успешность действий Step 1/2 будет высокой (). По мере увеличения количества агентов вероятность обнаружить в выбранной случайно ячейке свободное место снижается вместе с успешностью , если только выбор ячейки для совершения шага не будет делаться осознано. Когда количество агентов будет близко к максимальной емкости пространства () вероятность найти свободное место станет близкой к нулю (). Можно ввести параметр осознанности действий Step 1/2, который рассчитаем, как разность между текущей успешностью и вероятностью обнаружить свободное место в ячейке :
Здесь – обозначает вероятность присутствия в выбранной ячейке двух агентов.
Таким же образом успешность действий Attack и Sex будет зависеть от вероятности () что агент обнаружит в ячейке, которую он занимает, еще одного агента.
Осознанность совершения атаки можно определить как превышение успешности над вероятностью :
А вот успешность зависит не только от вероятности найти партнера в ячейке, но и от вероятности что партнер тоже совершает в данный момент действие Sex. Но даже если партнер оказался сговорчивым, для успешного полового акта необходимо что бы в окружающем пространстве нашлось место для малыша. Поэтому вероятность случайного успеха будет произведением вероятностей трех независимых событий: – в ячейке есть потенциальный партнер, – партнер так же совершает действие Sex, – в ячейке, которую выбрала мать для размещения ребенка, есть свободное место. Поэтому осознанность брачного поведения предлагаю определить таким образом:
2. Постановка задачи
Для вычисления введенных выше индексов осознанности необходимо научится рассчитывать две вероятности: и . Очевидно, что они зависят от плотности агентов в пространстве, а также от равномерности их распределения по пространству. Но для упрощения расчетов в дальнейшем будем предполагать равномерное распределения агентов по пространству. То есть будем считать, что эти вероятности не зависят от положения агента в пространстве.
Сформулируем задачу следующим образом.
Имеется пространство из ячеек. В одной ячейке может находится не более агентов. В этих ячейках располагаются агентов (). Необходимо определить вероятность того, что в выбранной ячейке с одним агентом будет находится еще один агент – . И вероятность того, что в выбранной ячейке будет агентов – .
Для решения данной задачи я применил два подхода. Первый – это расчет вероятности в классическом ее понимании, как отношение количества различных расстановок агентов, которые благоприятствуют искомому событию, к полному количеству расстановок агентов по ячейкам. Для вычислений воспользовался методом производящих функций.
Во втором подходе использовалось понятие частотной вероятности. Расчеты выполнялись с применением метода Монте-Карло. Вероятно, есть и другие способы вычислить эти вероятности, и возможно даже более простые. Буду благодарен за наводку на таковые.
3. Подсчет способов расстановки агентов
Вывод рекуррентной формулы
Предложенный ниже подход к расчету вероятностей позволяет решить поставленную задачу даже в более общей постановке, когда вместимости ячеек различны. Зададим вместимости ячеек пространства в виде последовательности , где – номер ячейки (от до ). Для удобства вычислений перенумеруем ячейки таким образом что бы у выбранной для определения вероятностей ячейки был номер .
Поставленную задачу можно свести к подсчёту количества способов расставить агентов по ячейкам пространства. Тогда вероятность – это отношение количества способов расстановки агентов, при которых в ячейку попадает хотя бы один агент, к полному количеству способов расставить агентов по ячейкам пространства. Для мира Dракош вместимость всех ячеек равна двум. Но при расчете вместимость ячейки принимается , т.к. изначально известно, что в этой ячейке уже есть один агент (см. определение вероятности выше).
Вероятность – это отношение количества способов расстановки агентов, при которых в ячейку попадает предельное для этой ячейки количество агентов – , к полному количеству способов расставить агентов по ячейкам пространства.
Обозначим через количество способов расставить агентов по ячейкам с по первую. Так же для вычислений нам понадобится знать количество свободных мест в ячейках с по первую – :
Рассмотрим процесс, при котором мы последовательно перебираем все ячейки пространства (от до ) и на каждом шаге помещаем в очередную ячейку – некоторое количество агентов – , пока не расставим все неразмещенных агентов или не исчерпаем все ячейки. В ячейку можно поместить от до агентов. Но если агентов осталось меньше максимальной вместимости ячейки, то в текущую ячейку можем поместить не более агентов. Таким образом .
Количество способов заполнить ячейку агентами – это сочетание без повторений из по :
Поместив агентов в ячейку , останется еще агентов для расстановки в ячейки с по . И каждому будет соответствовать способов расстановки оставшихся агентов. Произведение – даёт нам количество способов разместить агентов в ячейке и агентов по остальным ячейкам. Суммируя по всем допустимым значениям , получим искомое количество способов расстановки:
Для того что бы воспользоваться полученной рекуррентной формулой необходимо задать граничные условия:
- Если , т.е. у нас не осталось агентов которых можно поместить в ячейку, тогда у нас есть всего один способ выполнить расстановку агентов – никого не помещать в ячейку:
- Для последней ячейки так же есть только один способ расставить агентов – оставить все агентов в ней, но только если им хватит места:
- Если места не хватает для размещения агентов в ячейках с по , то способов заполнить ячейку нету:
Теперь можем записать выражения для вероятности :
где – это количество способов расстановки агентов, при которых в ячейку попадает один и более агентов:
Обратите внимание, здесь начинаем суммировать с единицы, т.к. нас интересуют те расстановки, при которых в ячейку попадает хотя бы один агент.
Выражения для вероятности :
где – это количество способов расстановки агентов, при которых в ячейку попадает предельное для этой ячейки количество агентов:
Пример вычисления вероятностей для S=5
Рассмотрим пример вычисления количества способов расстановки агентов по пяти ячейкам (), вместимость которых равна двум ().
Результаты вычислений сведены в таблицу:


Результаты вычислений сведены в таблицу:


Упрощение и переход приведенному виду
Количество расстановок очень быстро растет и уже для чисел двойной точности не хватит. Даже если воспользоваться пакетами символьных вычислений с произвольной точностью (например, Symbolic Math Toolbox и Variable-precision arithmetic в среде MatLab) останется проблема переполнения стека вызовов рекуррентной функции при больших размерах пространства. Поэтому полученные выше выражения необходимо преобразовать. А еще лучше вывести формулу, с помощью которой сразу вычисляется без необходимости считать предыдущие значения.
Первое что можно сделать это вынести из-под знака суммы .
Но прежде введем обозначение приведенного количества расстановок агентов по ячейкам, которое в раз меньше:
Маленький алгебраический трюк
Полное количество способов расстановки теперь будет:
Аналогично для , и после подстановки в получим:
Полное количество способов расстановки теперь будет:
Аналогично для , и после подстановки в получим:
И можем сократить выражения для вероятностей на факториал:
Где
После введения новых обозначения требуется переписать выражения для граничных условий. Для дальнейших выкладок удобнее представить граничные условия в следующем виде:
- , при , ;
- , при , ;
- , при , ;
- , при .
Полученные выражения для приведенных количеств расстановок смотрятся поинтереснее т.к. коэффициенты в рекуррентной формуле постоянны и не растут со скоростью факториала как в формулах выше. Но все равно быстро и надежно вычислить вероятности при размерах пространства порядка 104 не очень получится.
Пример вычисления вероятностей для S = 5 в приведенном виде
Самое время проверить что ничего не испорчено нашими упрощениями.


Следующим шагом предлагаю избавится аж от трех видов выражений для приведенного количества расстановок: , , . Для этого достаточно выразить вероятности через . Тут нам придется вспомнить что вместимость ячеек в мире Dракош везде , кроме выбранной ячейки в которой одно место уже занято и поэтому . Дальнейшие решение поставленной задачи в общей постановке (когда вместимость ячеек произвольна) существенно усложнит выкладки в и так затянувшемся погружении в мир комбинаторики.
Избавление
Распишем , , , согласно их основным формулам и подставим в выражения для и :
Готовые выражения для вероятностей теперь зависят только от приведенного количества способов расстановки агентов одного вида – :
Построение производящей функции
Осталось научится рассчитывать элементы последовательности для произвольно больших значений и . Порывшись в учебниках по комбинаторике я нашёл довольно популярный и мощный метод для решения всяческих комбинаторных вопросов – метод производящих функций.
Хорошим пособием для начинающих комбинаторов по производящим функциям можно назвать учебник Ландо С.К. [3]. Еще один ресурс типа справочник по производящим функциям. И еще вот этот пост на хабре. Но наиболее полезными для меня были видео лекции Игоря Клейна по производящим функциям, выложенные тут.
Но в перечисленных ресурсах в основном речь ведется о производящих функциях для одномерных последовательностей, с одним индексом. А наша последовательность двумерная, с двумя индексами. Производящие функции от двух переменных лишь упоминаются. Поэтому пришлось рискнуть и попробовать вывести производящую функцию для нашей двумерной последовательности на основе одномерных примеров.
Пару слов о том, что такое производящая функция последовательности
Это формальная замена последовательности , , , , … степенным рядом:
Идея метода в том, что получив каким-то из способов выражение для производящей функции можно затем разложить его в степенной ряд и тем самым, например, получить выражение для общего члена последовательности в замкнутом виде (не требующем вычисления предыдущих членов последовательности). Это как раз то, что нам требуется.
Идея метода в том, что получив каким-то из способов выражение для производящей функции можно затем разложить его в степенной ряд и тем самым, например, получить выражение для общего члена последовательности в замкнутом виде (не требующем вычисления предыдущих членов последовательности). Это как раз то, что нам требуется.
Суммируя то, что имеется на данный момент по нашей последовательности приведенных количеств расстановок запишем рекуррентную формулу для совместно с граничными условиями.
Наша последовательность зависит от двух индексов: – количество ячеек в пространстве для расстановки агентов, ; – количество агентов для расстановки в ячейках, . Поэтому и производящая функция ей нужна двумерная – .
Используя специальный технический примем можно из рекуррентного выражения для элементов последовательности получить выражение для производящей функции. У меня получилось вот это:
Тот самый технический прием
Суть приема в том, чтобы выписать первые элементы последовательности в столбик согласно рекуррентной формуле и умножить каждую строку на соответствующий множитель .
Просуммируем полученные выражения в столбик следующим образом. Отдельно суммируем левый от равно столбец и получим собственно производящую функцию —
Суммируя синие слагаемые справа от равно, получим:
Замете, что начиная со второго слагаемого можно вынести за скобки множитель и там останется наша производящая функция:
Суммируя зеленые слагаемые, получим:
Суммируя красные слагаемые, получим:
После выполненных суммирований получим уравнение относительно искомой функции:
Решая которое относительно получим выражение для производящей функции.
Просуммируем полученные выражения в столбик следующим образом. Отдельно суммируем левый от равно столбец и получим собственно производящую функцию —
Суммируя синие слагаемые справа от равно, получим:
Замете, что начиная со второго слагаемого можно вынести за скобки множитель и там останется наша производящая функция:
Суммируя зеленые слагаемые, получим:
Суммируя красные слагаемые, получим:
После выполненных суммирований получим уравнение относительно искомой функции:
Решая которое относительно получим выражение для производящей функции.
Теперь дело за малым, разложить полученную производящую функцию в ряд по степеням . Собственно, произвести элементы последовательности:
Процесс разложения в ряд
Для начала обозначим:
С учетом этих обозначений производящая функция запишется:
Вот тут лежит аж семь объяснений того почему это степенной ряд . С учетом этого наша функция раскладывается в ряд по степеням следующим образом:
Теперь разберемся с .
А это уже бином Ньютона:
Аналогично для :
Осталось подставить полученное выражение для в производящую функцию:
С учетом этих обозначений производящая функция запишется:
Вот тут лежит аж семь объяснений того почему это степенной ряд . С учетом этого наша функция раскладывается в ряд по степеням следующим образом:
Теперь разберемся с .
А это уже бином Ньютона:
Аналогично для :
Осталось подставить полученное выражение для в производящую функцию:
Теперь все что нам нужно это выделить коэффициент при , это и будет искомое выражение для элемента последовательности :
Для этого необходимо сгруппировать все слагаемые, у которых степень — равна . Пределы суммирования при этом будут следующими: при , ; при , .
В результате получим два выражения, одно для чётного :
и одно для нечетного :
Полученные выражения уже можно попробовать вычислить, но так как биноминальные коэффициенты, которые входят в них, всё же растут довольно быстро, для расчетов необходимо воспользовался инструментами символьных вычислений MatLab.
Пример реализации в MatLab
Вычисление .
Вычисление .
Вычисление .
function out = f(i,n)
%% Символьное вычисление f(i,n)
nu = ceil(n/2); % нижний предел суммирования
syms k
if mod(n,2)==0 % если n чётное
syms S(t,h)
S(t,h) = symsum(nchoosek(t,k)*nchoosek(k,2*h-k)/2^(2*h-k), k, h, 2*h);
out = S(i,nu);
else % если n нечётное
syms S(t,h)
S(t,h) = symsum(nchoosek(t,k)*nchoosek(k,2*h-k-1)/2^(2*h-k-1), k, h, 2*h-1);
out = S(i,nu);
end
Вычисление .
function out = W1sym(ii,N)
%% Символьное вычисление вероятности обнаружить второго агента в ячейке пространства
out = 1/(1 + f(ii-1,N-1)/f(ii-1,N-2));
Вычисление .
function out = W2sym(ii,N)
%% Символьное вычисление вероятности обнаружить второго агента в ячейке пространства
out = 1/(1 + 2*f(ii-1,N)/f(ii-1,N-2) + 2*f(ii-1,N-1)/f(ii-1,N-2));
4. Моделирование вероятностей методом Монте-Карло
Метод Монте-Карло или метод статистических испытаний — это большая группа численных методов решения математических задач (причем не только вероятностной природы) при помощи моделирования случайных величин. Один из вариантов метода Монте-Карло предполагает что смоделированная случайная величина с известным распределением (зачастую равномерно распределённая на отрезке 0..1) используется для установления статистических характеристик других случайных величин или для приближённой оценки некоторого значения . Во втором случае придумывается некоторая случайная величина , такая что ее мат. ожидание равно искомой величине . Тогда рассчитав независимых значений случайной величины , , …, определяют величину как среднее арифметическое выборки , …, [2].
Для установления статистических характеристик случайных величин, например, для определения вероятности случайного события , можно реализовать другой вариант метода Монте-Карло. Когда проводится моделирование такой случайной величины , которая равна при реализации случайного события на испытании , или равна если события не наступило. При проведении независимых испытаний частота события , равная , стремится к искомой вероятности по мере роста количества испытаний [3]. Если для моделирования случайной величины в модели полностью или частично воспроизводится изучаемый естественный процесс, то такой подход так же называют – имитационным моделированием.
На сегодня метод имитационного моделирования развился в самостоятельное направление методов исследований. Но для решения поставленной в разделе 2 задачи использовался подход, который с одной стороны является примером реализации методов Монтер-Карло, с другой это пример имитационного моделирования, т.к. использовался «естественный» процесс изменения положения агентов в пространстве.
Обзор алгоритма
В рамках метода Монте-Карло поставленная в разделе 2 задача сводится к оценке частоты реализации соответствующих событий. Так вероятность – это частота обнаружения агентами соседей по ячейке. А вероятность – это частота обнаружения ячеек с двумя агентами.
Будем рассматривать процесс заполнения ячеек агентами, так что в одной ячейке может быть не более агентов. На каждом шаге будем пересаживать агентов в новые ячейки, и если при попытке пересадить агента окажется что в выбранной ячейке нет свободного места, то оставляем агента на старом месте.

После каждого этапа пересаживаний будем подсчитывать количество полностью заполненных ячеек (с двумя агентами).
Частота обнаружения ячеек с двумя агентами (вероятность ) это просто:
Можно предложить несколько вариантов реализации этапа пересаживания:
- Scenario 1 – почти полная имитация: для пересаживания случайно выбираются 50% агентов и каждый из них пересаживается в одну из 18 соседних клеток выбранных случайно;
- Scenario 2 – пересаживаются все агенты и каждый из них пересаживается в одну из 18 соседних клеток выбранную случайно;
- Scenario 3 – для пересаживания случайно выбираются 50% агентов и каждый из них пересаживается в случайную ячейку пространства;
- Scenario 4 – пересаживаются все агенты и каждый из них пересаживается в случайную ячейку пространства;
Scenario 1 назван почти полной имитацией процессов в настоящем мире Dракош, так как доля агентов совершающих действия Step 1/2 различна для каждого такта времени и может иметь любое значение а не только 50%. Ниже мы посмотрим, как результаты вычислений зависят от сценария пересаживания агентов.
Процесс начинаем со случайной расстановки агентов по ячейкам. Затем в цикле раз повторяются два этапа:
- Пересаживаем агентов согласно выбранного сценария;
- Определяем количество заполненных ячеек – и соответствующие значения и .
Возникает вопрос: сколько же раз необходимо повторить цикл? С ростом неопределенность вычислений убывает пропорционально . Т.е. для увеличения точности в 10 раз необходимо увеличить количество испытаний в 100 раз. Метод Монте-Карло похож на натурные физические эксперименты в том плане что точность результатов можно определить только после получения результата эксперимента. Точнее случайную составляющую неопределенности. И так же как в натурном эксперименте ею можно управлять изменяя количество измерений.
На графике ниже показана зависимость вероятности для и () от количества испытаний. Для каждой точки показаны планки неопределенности, которая рассчитывалась на основе стандартного отклонения полученных выборок и коэффициента охвата (надежность 99.7%).
Горизонтальной чертой отмечено точное значение, рассчитанное способом, описанным в разделе 3.

По результатам расчетов получены следующие значения неопределенности (надежность 99.7%):
- Для неопределенность составила 0.0014 (0.24%);
- Для – 0.00047 (0.080%);
- Для – 0.00015 (0.025%);
- Для – 0.000066 (0.011%);
Т.к. время вычислений растет пропорционально количеству испытаний (для составило около 6.5 часов), а желания сильно оптимизировать код у меня не было, решено было для последующих экспериментов использовать по 1000 испытаний.
Результаты Монте-Карло
Давайте посмотрим, как зависит рассчитываемые значения вероятностей от используемого сценария пересаживания агентов. Ниже показаны результаты вычислений для разных сценариев, при и () и количестве испытаний по .

Как можно видеть отличия между рассчитанными значениями вероятностей с использованием разных сценариев намного меньше неопределенности этих результатов. Это позволяет заключить что более точная имитации мира Dракош привела бы к такому же результату. Поэтому не зачем тратить время.
5. Что получилось?
На графике ниже показаны зависимость вероятностей и от плотности агентов в пространстве. Синяя и красная области — это массивы данных, насчитанные методом Монте-Карло (по 1000 итераций для каждого значения ). Черные линии — это точные значения, вычисленные методом, описанным в разделе 3.

Совпадение результатов, полученных разными методами, позволяет надеяться, что серьезных ошибок не было допущено.
Теперь можем посмотреть, как выглядит успешность действий Step 1/2, Attack и Sex при полностью случайном (неосознанном) поведении агентов. А точнее на вторые слагаемые в выражениях для индексов осознанности, которые как раз и задают базовый уровень успешности, обусловленный вероятностями обнаружения агентов в пространстве:
Для однозначности примем что частота действия Sex – (т.е. если партнер был замечен в ячейке, то он принимает участие в размножении

В дальнейшем мы сравним полученные результаты с успешностью Тупиков (раса агентов без нейронной сети) и полноценных Dракош и посмотрим, как будет расти успешность в результате развития нейронной сети агентов.
- Ландо С.К. Лекции о производящих функциях. 2007. 144 c.
- Соболь И.М. Численные методы Монте-Карло. 1973. 312 с.
- Бусленко Н.П., Шрейдер Ю.А. Метод статистических испытаний (Монте-Карло) и его реализация на цифровых вычислительных машинах. 1961. 226 с.

