В этом туториале я расскажу о том, как освоить инверсную кинематику в 3D: методику, позволяющую решить задачу перемещения манипулятора робота к определённой цели.
Об инверсной кинематике в 2D можно прочитать здесь:
Ссылка на скачивание всего пакета Unity находится в конце туториала.
В моём блоге часто повторяются некоторые темы: одной из них, без всяких сомнений, является инверсная кинематика. Я работал с этой восхитительной темой уже в двух сериях туториалов, в сумме составляющих 8 статей. Тем не менее, ещё многое можно написать об инверсной кинематике в контексте видеоигр.
Почему инверсная кинематика настолько интересна и сложна, что требует такого количества постов? Дело в том, что инверсная кинематика часто встречается не только в видеоиграх, но и в инженерном проектировании, а также в науке в целом. От проектирования манипуляторов роботов до понимания управления моторикой в человеческом мозге — во всём этом важную роль в том или ином виде играет инверсная кинематика.
Первая серия, посвящённая этой теме, An Introduction to Procedural Animations [перевод на Хабре], вышла в 2017 году, ещё сильнее популяризировав термин "процедурные анимации" в среде инди-разработчиков. В ней представлено общее решение на основании алгоритма градиентного спуска, которое потенциально можно использовать для довольно «экзотических» моделей, например, щупалец или паучьих ног.
Вторая серия, Inverse Kinematics in 2D, вышла годом позже, в ней рассматривался очень специфический случай: двухшарнирный манипулятор, ограниченный 2D-плоскостью (см. ниже). Суть можно понять из названия: инверсная кинематика в 2D. Каждый из двух шарниров контролируется углом и . При изменении этих двух углов конец манипулятора, называемый конечным звеном, достигает различных точек.
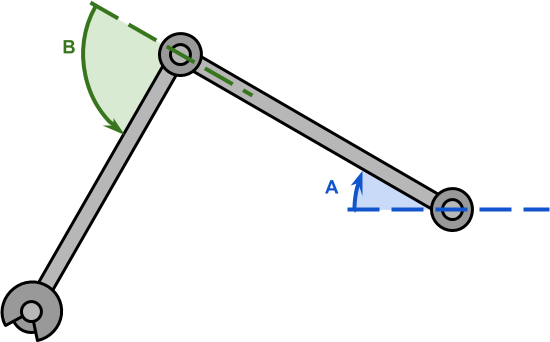
Задача инверсной кинематики (ИК) заключается в нахождении углов и , таких, чтобы конечное звено достигало нужной целевой точки. В анимации показан манипулятор, рисующий окружность на плоскости XY.
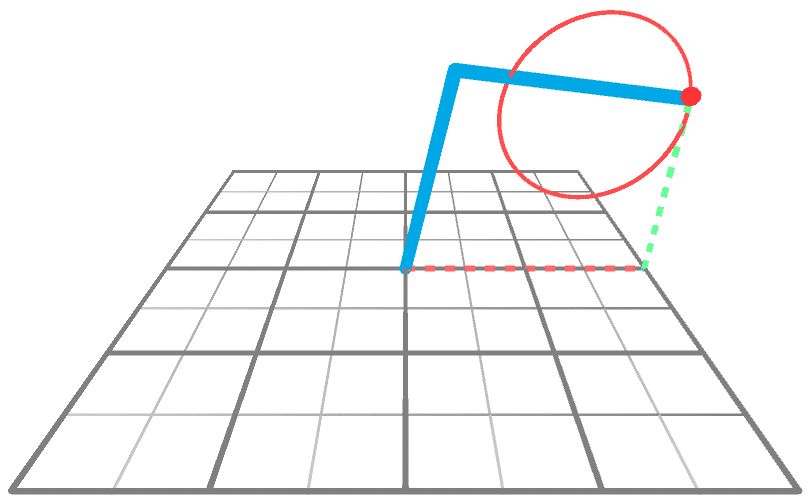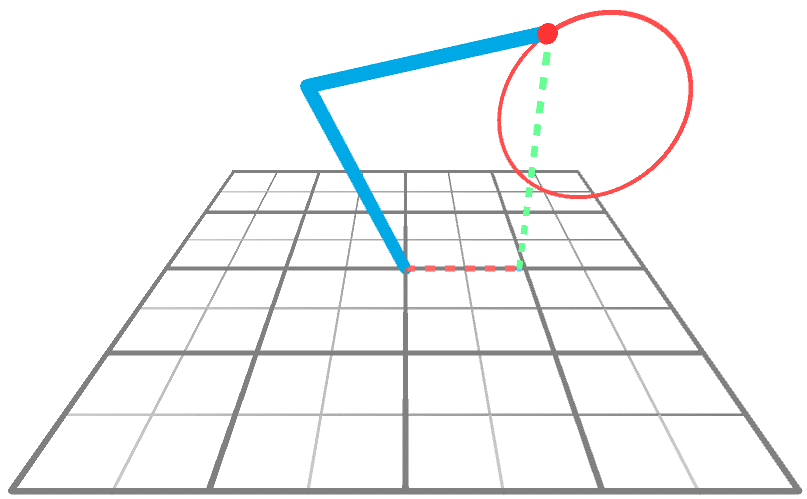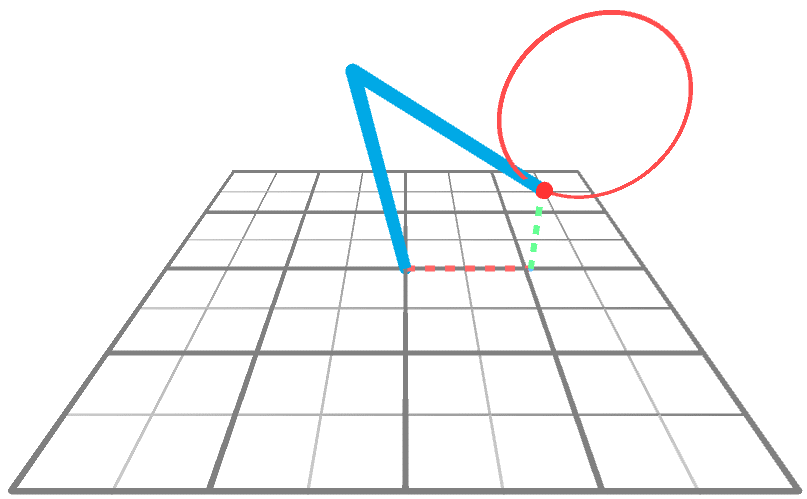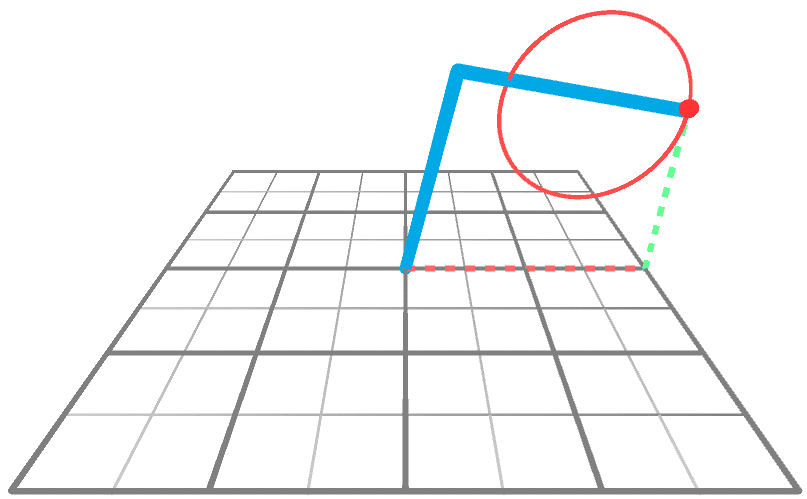
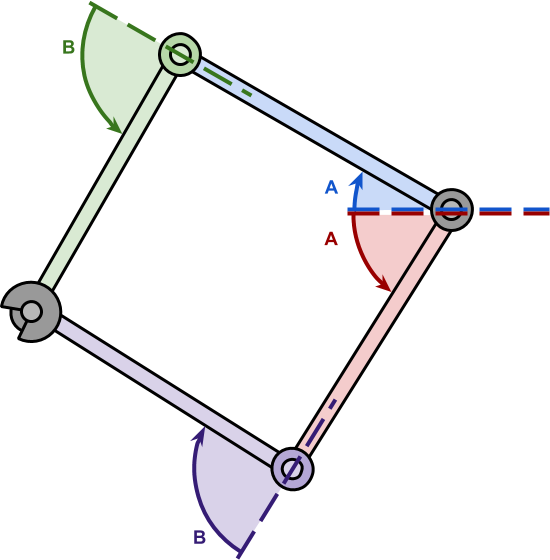
Строго говоря, решение, представленное в Inverse Kinematics for Robotic Arms, потенциально может работать с любым количеством шарниров. Так почему же мы сосредоточились на менее мощной методике? Ответ прост: эффективность. Об этом стоило написать потому, что в описанном выше сценарии решение можно найти при помощи простого уравнения, а не достаточно сложного алгоритма. Это возможно благодаря тому, что мы можем представить манипулятор робота как треугольник (см. ниже) с двумя внутренними углами и .

Применив простую тригонометрию, мы выяснили, что значения таких углов будут равны:
(1)
(2)
где , и — стороны этого построенного нами «воображаемого» треугольника.
Однако шарниры манипулятора управляются при помощи и , которые оказываются равными:
(3)
(4)
где:
(5)
Если вы ранее читали серию Inverse Kinematics in 2D, то для вас в предыдущем разделе не было ничего нового. Если не читали, то не волнуйтесь: этого вполне будет достаточно.
Этот упрощённый случай стоит обсудить потому, что его можно использовать в качестве начальной точки для решения задачи ИК в 3D.
Во-первых, нам нужно понять, что сценарий с двухшарнирным манипулятором в 2D — это задача с двумя степенями свободы (2DOF). В противоположность тому, что можно представить, это не значит, что у нас есть два сегмента; на самом деле, у нас есть контроль над двумя переменными (которые, в данном случае, оказываются углами шарниров).
Когда мы расширяем эту задачу на третье измерение, наш манипулятор по-прежнему имеет два сегмента и два шарнира. Однако теперь задача имеет три степени свободы (3DOF), если предположить, что мы можем ещё и свободно вращать манипулятор вокруг первого шарнира.
При таком сценарии второй шарнир () остался неизменным. Однако, мы предполагаем, что первый () теперь может свободно вращаться в другом измерении. Из-за этого первый шарнир часто называют бедром, а второй — коленом. Колено человека имеет одну степень свободы (вперёд-назад), а бедро — две (вперёд-назад и внутрь-наружу). Угол, на который вращается бедро, обозначается .
Мы можем представить манипулятор робота, у которого оба шарнира имеют две степени свободы, что в сумме даёт четыре. Проблема здесь заключается в том, что может быть много решений, из-за чего наш подход перестаёт быть эффективным. «Ногоподобные» манипуляторы (то есть имеющие шарниры бедра и колена) очень распространены и в играх, и в промышленности. Поэтому, вероятно, стоит изучить этот подход.
Если вы читали предыдущие статьи, то можете помнить, что если цель достижима в 2D, то всегда существует два «зеркальных» решения (см. ниже).
Та же проблема возникает и в 3D; однако в этом случае решений бесконечно много. Конфигурация может вращаться вокруг оси симметрии, представленной прямой линией, соединяющей начальную точку с целью. Чтобы решить задачу, нужно сосредоточиться только на одном решении! В этом туториале мы рассмотрим решение, которое найти проще всего, оно предполагает, что (0, 1, 0) — это направление «вверх».
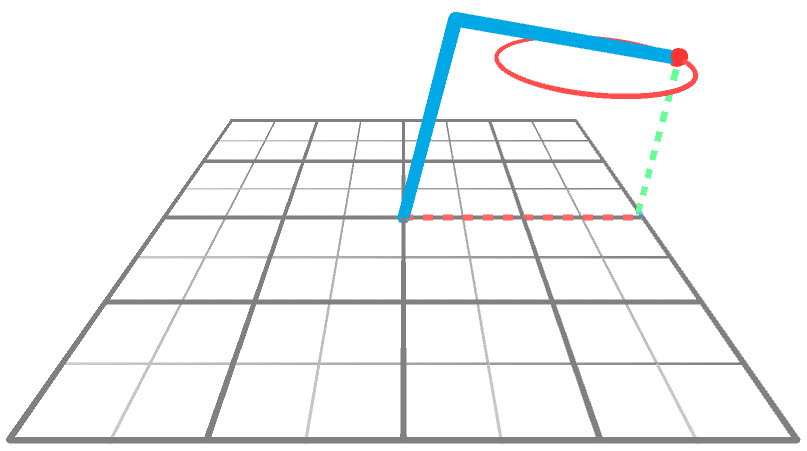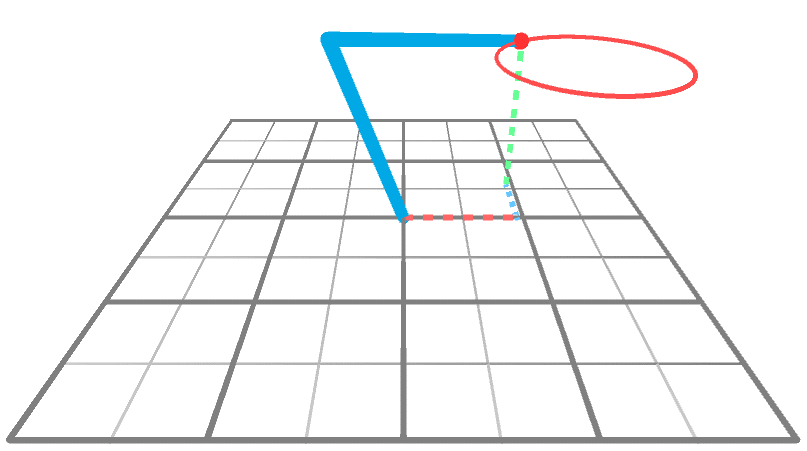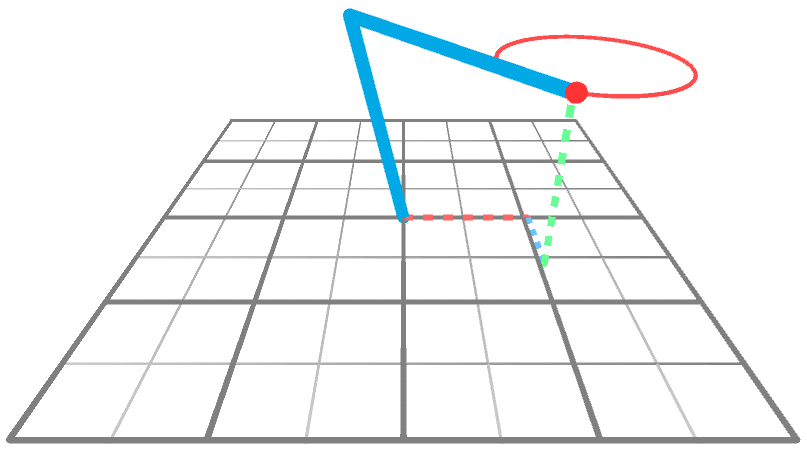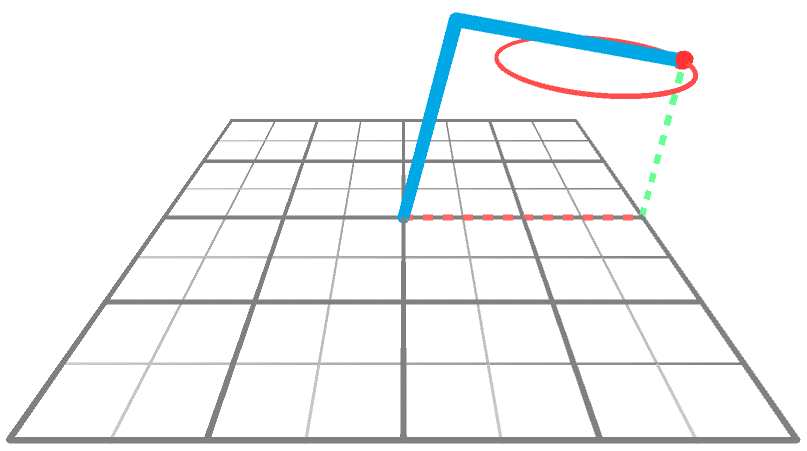
Пока мы знаем только, как решить задачу ИК, когда движение ограничено плоскостью XY. Хитрость при переходе из 2D в 3D заключается в том, чтобы снова использовать 2D-решение. В анимации показан манипулятор, движущийся к точке в 3D-пространстве, вращающейся вокруг оси Y. Довольно очевидно, что единственное, что делает манипулятор — это тоже вращается; его углы и не меняются, меняется только .

Это означает, что если мы знаем, как выполнить ИК на плоскости XY (а мы знаем!), то и знаем, как выполнить её во всём пространстве XYZ при помощи двух простых поворотов. В целом, можно решить эту задачу в три этапа:
Это можно сделать эффективнее, просто выполнив ИК в 2D не на плоскости XY, а на вертикальной плоскости, проходящей из опорной точки манипулятора к целевой точке.
Чтобы выполнить ИК в 3D, нам первым делом нужно вычислить , то есть угол, на который вращается весь манипулятор. Это дополнительная степень свободы, добавленная к шарниру бедра.
Удобнее всего найти его, предположив, что манипулятор уже достиг позиции (то есть уже находится в целевой позиции) и вычислив получившийся угол . Так как — это угол, на который переместилось бедро по оси Y, мы можем смотреть на манипулятор ровно сверху. При виде сверху на плоскость XZ (см. ниже) манипулятор выглядит как отрезок прямой. Так получилось, потому что за исключением бедра два остальных шарнира ограничены плоскостью.

Если мы рассмотрим отрезок как гипотенузу прямоугольного треугольника, то при помощи тригонометрии сможем вычислить угол :
(6)
Строго говоря, знания более чем достаточно для решения ИК в 3D. На самом деле, мы можем реализовать алгоритм, описанный в предыдущем разделе: повернуть целевую точку на градусов по оси Y, выполнить ИК на плоскости XY, а затем повернув весь манипулятор на градусов.
Быстрее было бы выполнить ИК не на 2D-плоскости, а непосредственно на вертикальной плоскости, проходящей через шарнир бедра и целевую точку. Однако, кое-что мешает нам это сделать. Давайте ещё раз взглянем на схему со всеми используемыми углами:

Чтобы вычислить , то есть угол, контролирующий первый шарнир, нам нужно вычислить . Это угол между первым шарниром и целевой точкой. Если вспомнить уравнение (5), использованное для вычисления , то мы заметим серьёзную проблему: оно предполагает, что все точки находятся на плоскости XY:
В нашем 3D-сценарии манипулятор, к сожалению, будет вращаться на по оси Y. Однако новая схема остаётся почти такой же, если мы повернём вид вмести с манипулятором. Мы назовём эту новую систему координат WY, потому что ось X теперь заменена на W, которая была осью X, не повёрнутой на градусов по оси Y.

Мы не можем просто выполнить , как делали это с , потому что хотя и параллельны оси Y, и не параллельны оси X. Они параллельны оси W. Следовательно, лучшим способом вычисления будет получение расстояния от до . При этом теряется знак , однако, к счастью, это не вызовет проблем в наших вычислениях. Если манипулятор будет двигаться в противоположном направлении, то мы просто сменим знак в коде.
(9)
где — длина отрезка от до . Её можно легко вычислить функцией наподобие
(10)
В показанном выше уравнении вклад Y из теоремы Пифагора сокращается, потому что точка имеет ту же компоненту Y, что и , поэтому их равна нулю.
Теперь у нас есть всё для выполнения ИК в 3D для манипулятора робота с одним коленом и одним бедром:
(11)
(12)
(13)
Хотя уравнения выглядят пугающе, их легко реализовать и они позволяют максимально бысро выполнять ИК в 3D.
В следующем туториале этой серии я покажу, как использовать ИК для создания реалистичных многоногих существ. Да, долгожданный туториал по ИК паучьих ног наконец появится!

Скачать все использованные в этом туториале ассеты с полнофункциональным манипулятором для Unity можно, подписавшись на мой Patreon.
Об инверсной кинематике в 2D можно прочитать здесь:

Ссылка на скачивание всего пакета Unity находится в конце туториала.
Введение
В моём блоге часто повторяются некоторые темы: одной из них, без всяких сомнений, является инверсная кинематика. Я работал с этой восхитительной темой уже в двух сериях туториалов, в сумме составляющих 8 статей. Тем не менее, ещё многое можно написать об инверсной кинематике в контексте видеоигр.
Почему инверсная кинематика настолько интересна и сложна, что требует такого количества постов? Дело в том, что инверсная кинематика часто встречается не только в видеоиграх, но и в инженерном проектировании, а также в науке в целом. От проектирования манипуляторов роботов до понимания управления моторикой в человеческом мозге — во всём этом важную роль в том или ином виде играет инверсная кинематика.
Краткое описание
Первая серия, посвящённая этой теме, An Introduction to Procedural Animations [перевод на Хабре], вышла в 2017 году, ещё сильнее популяризировав термин "процедурные анимации" в среде инди-разработчиков. В ней представлено общее решение на основании алгоритма градиентного спуска, которое потенциально можно использовать для довольно «экзотических» моделей, например, щупалец или паучьих ног.
Вторая серия, Inverse Kinematics in 2D, вышла годом позже, в ней рассматривался очень специфический случай: двухшарнирный манипулятор, ограниченный 2D-плоскостью (см. ниже). Суть можно понять из названия: инверсная кинематика в 2D. Каждый из двух шарниров контролируется углом и . При изменении этих двух углов конец манипулятора, называемый конечным звеном, достигает различных точек.

Задача инверсной кинематики (ИК) заключается в нахождении углов и , таких, чтобы конечное звено достигало нужной целевой точки. В анимации показан манипулятор, рисующий окружность на плоскости XY.

Строго говоря, решение, представленное в Inverse Kinematics for Robotic Arms, потенциально может работать с любым количеством шарниров. Так почему же мы сосредоточились на менее мощной методике? Ответ прост: эффективность. Об этом стоило написать потому, что в описанном выше сценарии решение можно найти при помощи простого уравнения, а не достаточно сложного алгоритма. Это возможно благодаря тому, что мы можем представить манипулятор робота как треугольник (см. ниже) с двумя внутренними углами и .

Применив простую тригонометрию, мы выяснили, что значения таких углов будут равны:
(1)
(2)
где , и — стороны этого построенного нами «воображаемого» треугольника.
Однако шарниры манипулятора управляются при помощи и , которые оказываются равными:
(3)
(4)
где:
(5)
Показать вывод уравнения
.Полный вывод можно найти в статье Inverse Kinematics in 2D: The Mathematics
Переходим в три измерения
Если вы ранее читали серию Inverse Kinematics in 2D, то для вас в предыдущем разделе не было ничего нового. Если не читали, то не волнуйтесь: этого вполне будет достаточно.
Этот упрощённый случай стоит обсудить потому, что его можно использовать в качестве начальной точки для решения задачи ИК в 3D.
Во-первых, нам нужно понять, что сценарий с двухшарнирным манипулятором в 2D — это задача с двумя степенями свободы (2DOF). В противоположность тому, что можно представить, это не значит, что у нас есть два сегмента; на самом деле, у нас есть контроль над двумя переменными (которые, в данном случае, оказываются углами шарниров).
Когда мы расширяем эту задачу на третье измерение, наш манипулятор по-прежнему имеет два сегмента и два шарнира. Однако теперь задача имеет три степени свободы (3DOF), если предположить, что мы можем ещё и свободно вращать манипулятор вокруг первого шарнира.
При таком сценарии второй шарнир () остался неизменным. Однако, мы предполагаем, что первый () теперь может свободно вращаться в другом измерении. Из-за этого первый шарнир часто называют бедром, а второй — коленом. Колено человека имеет одну степень свободы (вперёд-назад), а бедро — две (вперёд-назад и внутрь-наружу). Угол, на который вращается бедро, обозначается .
Мы можем представить манипулятор робота, у которого оба шарнира имеют две степени свободы, что в сумме даёт четыре. Проблема здесь заключается в том, что может быть много решений, из-за чего наш подход перестаёт быть эффективным. «Ногоподобные» манипуляторы (то есть имеющие шарниры бедра и колена) очень распространены и в играх, и в промышленности. Поэтому, вероятно, стоит изучить этот подход.
Если вы читали предыдущие статьи, то можете помнить, что если цель достижима в 2D, то всегда существует два «зеркальных» решения (см. ниже).

Та же проблема возникает и в 3D; однако в этом случае решений бесконечно много. Конфигурация может вращаться вокруг оси симметрии, представленной прямой линией, соединяющей начальную точку с целью. Чтобы решить задачу, нужно сосредоточиться только на одном решении! В этом туториале мы рассмотрим решение, которое найти проще всего, оно предполагает, что (0, 1, 0) — это направление «вверх».
Из 2D в 3D
Пока мы знаем только, как решить задачу ИК, когда движение ограничено плоскостью XY. Хитрость при переходе из 2D в 3D заключается в том, чтобы снова использовать 2D-решение. В анимации показан манипулятор, движущийся к точке в 3D-пространстве, вращающейся вокруг оси Y. Довольно очевидно, что единственное, что делает манипулятор — это тоже вращается; его углы и не меняются, меняется только .

Это означает, что если мы знаем, как выполнить ИК на плоскости XY (а мы знаем!), то и знаем, как выполнить её во всём пространстве XYZ при помощи двух простых поворотов. В целом, можно решить эту задачу в три этапа:
- Поворачивать целевую точку вокруг оси Y, пока она не окажется на плоскости XY
- Переместить манипулятор робота так, чтобы он смог достичь точки, как если бы она была в 2D
- «Отменить» поворот, повернув весь манипулятор в противоположном направлении по оси Y.
Это можно сделать эффективнее, просто выполнив ИК в 2D не на плоскости XY, а на вертикальной плоскости, проходящей из опорной точки манипулятора к целевой точке.
Поворот вокруг оси Y
Чтобы выполнить ИК в 3D, нам первым делом нужно вычислить , то есть угол, на который вращается весь манипулятор. Это дополнительная степень свободы, добавленная к шарниру бедра.
Удобнее всего найти его, предположив, что манипулятор уже достиг позиции (то есть уже находится в целевой позиции) и вычислив получившийся угол . Так как — это угол, на который переместилось бедро по оси Y, мы можем смотреть на манипулятор ровно сверху. При виде сверху на плоскость XZ (см. ниже) манипулятор выглядит как отрезок прямой. Так получилось, потому что за исключением бедра два остальных шарнира ограничены плоскостью.

Если мы рассмотрим отрезок как гипотенузу прямоугольного треугольника, то при помощи тригонометрии сможем вычислить угол :
(6)
Вывод уравнения
Вычисление угла между двумя точками — довольно частая задача для разработчиков игр и решить её можно тригонометрически.
Хитрость в данном случае заключается в том, чтобы добавить наклон линии (см. ниже), который является соотношением её подъёма () и пролёта (). Наклон прямой можно вычислить между двумя любыми точками и он везде даст одинаковый результат.
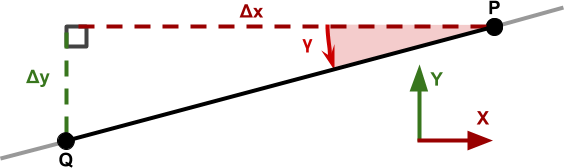
Наклон прямой имеет прямую связь с углом прямой :
(7)
Если вы изучали тригонометрию, то должны понять, что подъём на самом деле является , а пролёт — . А функция тангенса, по определению — это соотношение синуса и косинуса.
Чтобы извлечь из (7), можно использовать функцию, обратную тангенсу, то есть арктангенс:
(8)
Всё это замечательно работает в теории, однако существуют проблемы со знаком и . На самом деле, наклон даёт одинаковый результат, когда и одновременно являются или отрицательными, или положительными. Однако с геометрической точки зрения это соответствует двум противоположным углам! Решение заключается в том, чтобы использовать не напрямую, а его «программного» близкого родственника
Хитрость в данном случае заключается в том, чтобы добавить наклон линии (см. ниже), который является соотношением её подъёма () и пролёта (). Наклон прямой можно вычислить между двумя любыми точками и он везде даст одинаковый результат.

Наклон прямой имеет прямую связь с углом прямой :
(7)
Если вы изучали тригонометрию, то должны понять, что подъём на самом деле является , а пролёт — . А функция тангенса, по определению — это соотношение синуса и косинуса.
Чтобы извлечь из (7), можно использовать функцию, обратную тангенсу, то есть арктангенс:
(8)
Всё это замечательно работает в теории, однако существуют проблемы со знаком и . На самом деле, наклон даёт одинаковый результат, когда и одновременно являются или отрицательными, или положительными. Однако с геометрической точки зрения это соответствует двум противоположным углам! Решение заключается в том, чтобы использовать не напрямую, а его «программного» близкого родственника
atan2. В большинстве фреймворков существует реализация функции арктангенса, получающая два параметра, обычно называемые dy и dx.Инверсная кинематика на плоскости WY
Строго говоря, знания более чем достаточно для решения ИК в 3D. На самом деле, мы можем реализовать алгоритм, описанный в предыдущем разделе: повернуть целевую точку на градусов по оси Y, выполнить ИК на плоскости XY, а затем повернув весь манипулятор на градусов.
Быстрее было бы выполнить ИК не на 2D-плоскости, а непосредственно на вертикальной плоскости, проходящей через шарнир бедра и целевую точку. Однако, кое-что мешает нам это сделать. Давайте ещё раз взглянем на схему со всеми используемыми углами:

Чтобы вычислить , то есть угол, контролирующий первый шарнир, нам нужно вычислить . Это угол между первым шарниром и целевой точкой. Если вспомнить уравнение (5), использованное для вычисления , то мы заметим серьёзную проблему: оно предполагает, что все точки находятся на плоскости XY:
В нашем 3D-сценарии манипулятор, к сожалению, будет вращаться на по оси Y. Однако новая схема остаётся почти такой же, если мы повернём вид вмести с манипулятором. Мы назовём эту новую систему координат WY, потому что ось X теперь заменена на W, которая была осью X, не повёрнутой на градусов по оси Y.

Мы не можем просто выполнить , как делали это с , потому что хотя и параллельны оси Y, и не параллельны оси X. Они параллельны оси W. Следовательно, лучшим способом вычисления будет получение расстояния от до . При этом теряется знак , однако, к счастью, это не вызовет проблем в наших вычислениях. Если манипулятор будет двигаться в противоположном направлении, то мы просто сменим знак в коде.
(9)
где — длина отрезка от до . Её можно легко вычислить функцией наподобие
Vector3.Distance, или просто применить теорему Пифагора:(10)
В показанном выше уравнении вклад Y из теоремы Пифагора сокращается, потому что точка имеет ту же компоненту Y, что и , поэтому их равна нулю.

Теперь у нас есть всё для выполнения ИК в 3D для манипулятора робота с одним коленом и одним бедром:
(11)
(12)
(13)
Хотя уравнения выглядят пугающе, их легко реализовать и они позволяют максимально бысро выполнять ИК в 3D.
Что дальше
В следующем туториале этой серии я покажу, как использовать ИК для создания реалистичных многоногих существ. Да, долгожданный туториал по ИК паучьих ног наконец появится!

Скачивание пакета Unity
Скачать все использованные в этом туториале ассеты с полнофункциональным манипулятором для Unity можно, подписавшись на мой Patreon.

