29.04.2021 06:56
PatientZero 18 6200 Источник
Во многих современных играх присутствуют провода, кабели и цепи. В этой статье мы рассмотрим математические модели, от которых зависит их форма, также называемая catenary («цепная линия»).

Введение в цепные линии


Из множества изученных и описанных математических объектов один очень дорог многим разработчикам игр. И только некоторые из них знают его истинное название: цепная линия.

Цепная линия — это фигура, к которой естественным образом сводится подвешенная за края верёвка или цепь. Неслучайно само название catenary происходит от латинского catenaria, что и означает «цепь».

В современных играх появляется всё больше заброшенных предприятий и разрушенных окружений. И во многих из них встречается довольно много свисающих проводов. Например, их можно увидеть в комнате GLaDOS из «Portal» или в «Half-Life: Alyx».


Так как цепные линии окружают нас повсюду, неудивительно, что мы с детства привыкли к их форме. А ещё это означает, что мы очень легко замечаем, когда что-то свисает неправильно. Подобно сложности движения кожи или физики ткани, неправильное свисание цепных линий само по себе создаёт эффект «зловещей долины».


Тем не менее, в очень многих играх цепные линии реализуют неправильно! Однако причина этого неудивительна. Хоть их так легко создавать в реальной жизни, их математическое описание — настоящий кошмар. За исключением нескольких особых случаев, «простых» уравнений для генерации цепной линии не существует; по крайней мере, не в том виде, который нужен для украшения уровня.

Один из стандартных способов создания физически обоснованных цепных линий без затрат — использование твёрдых тел (rigid bodies) и шарниров (hinge joints) при создании цепей и верёвок. Это имеет и дополнительное преимущество — они реагируют на действия игрока, однако ценой затратных вычислений. Большинство свисающих проводов и кабелей является частью фона, и использовать физику для их создания было бы слишком затратно. Следовательно, очень важно иметь возможность создавать статические цепные линии без вычислений в реальном времени.

Кроме того, отрисовка цепных линий имеет ещё одно преимущество. Допустим, что нам нужно создать для игры настоящий, управляемый физикой свисающий провод. Как располагать сегменты провода при его создании в игре? Многие разработчики бы просто разместили их вдоль линии, позволив физическому движку самому выбрать равновесное состояние. Отрисовка цепных линий позволяет инициализировать физически верные провода и кабели уже в их состоянии равновесия, без необходимости ждать, пока они сами остановятся в нужном положении.

Стоит заметить, что в Unity нет встроенных инструментов для кабелей и цепей, а в Unreal Engine существует Cable Component, решающий как раз эту задачу при помощи техники Verlet Integration (которая станет темой моих будущих статей). А на случай, если вам нравятся шейдеры, Росс Бёрдсэлл недавно создал гениальное решение для симуляции спиральных шнуров в Unreal Engine 4.


Формальное определение


Если мы хотим получить физически корректные цепные линии, то, наверно, лучше начать с начала. Простейшая цепная линия задаётся однозначно определённым уравнением с использованием $\cosh$ — гиперболического косинуса:

$$display$$\begin{equation*} y=a \cosh{\left(\frac{x}{a}\right)}\end{equation*} (1)$$display$$


Уравнение цепной линии имеет параметр $a$, меняющий общую «ширину» кривой. Однако все кривые цепных линий похожи, потому что все они являются версиями друг друга с разным масштабом. Ниже показано изменение кривой как функции от $a$ (в оригинале статьи анимация интерактивна):


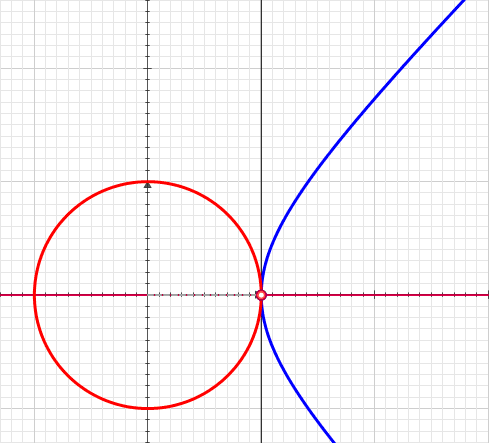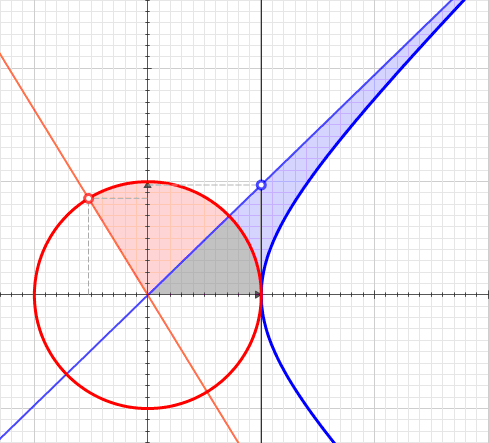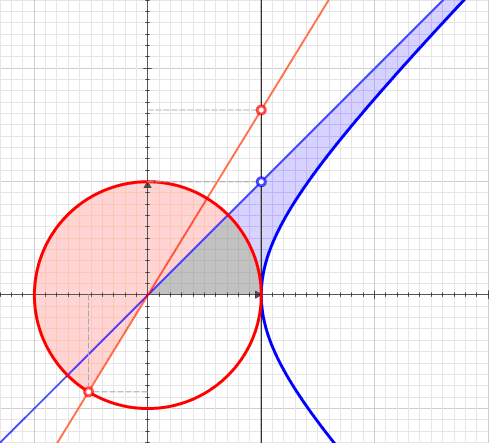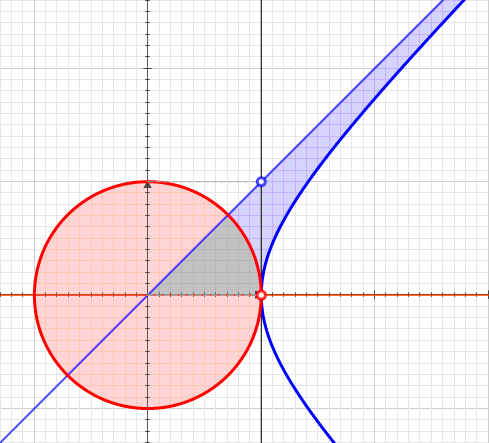
Что такое гиперболический косинус?
Многие из вас знакомы с более «традиционной» функцией косинуса. Синус и косинус задаются на окружности, а их гиперболические аналоги — на гиперболе (см. анимацию ниже).


Их естественной областью использования является изучение гиперболической геометрии. Также они часто оказываются решением множества дифференциальных уравнений. На самом деле, $\sinh$ и $\cosh$ играют важную роль в решении следующего дифференциального уравнения:

$f^{\prime\prime}=f$


а именно:

$f{\left(x\right)}=a \sinh {\left(x\right)}+b \cosh{\left(x\right)}$


Также они сильно связаны с ${\rm e}^{x}$:

$\begin{split}\sinh{x} & = \frac{{\rm e}^{x}-{\rm e}^{-x}}{2} \\\cosh{x} & = \frac{{\rm e}^{x}+{\rm e}^{-x}}{2} \\\end{split}$


Покажите, как выводится уравнение!
Вывод уравнения цепной линии — сложная задача, требующая довольно продвинутого математического анализа. Если вам любопытно, на Math24 есть очень подробная статья Equation of Catenary, пошагово демонстрирующая его вывод.

Вывод уравнения начинается с допущения о том, что для каждого небольшого сегмента цепи гравитационные силы находятся в идеальном балансе с силой натяжения от соседних сегментов. Это приводит к созданию системы уравнений, при решении которой мы получаем (1):

$y=a \cosh{\left(\frac{x}{a}\right)} $


Этот вывод также даёт нам некое понимание того, что же на самом деле означает параметр $a$:

$ a = \frac{T_0}{? g A}$


где:

  • $?$: плотность материала цепи;
  • $g$: ускорение силы тяжести;
  • $A$: площадь поперечного сечения цепи;
  • $T_0$: горизонтальная компонента силы натяжения, которой подвержен каждый сегмент цепи. Считается константой, потому что цепная линия рассматривается как фигура, которую принимает цепь, когда вес равномерно распределён вдоль кривой.

Как используют цепные линии?
Кроме использования для воссоздания висящих цепей, цепные линии особенно полезны во множестве других областей применения. Их форма образуется благодаря тщательному балансу между внутренним натяжением цепи и силой гравитации. Такое равновесие означает, что вес самой цепи равномерно распределён вдоль всей длины. Благодаря этому перевёрнутые цепные линии становятся идеальной формой для свободно стоящих арок постоянной толщины.

Доктор Том Кроуфорд рассказывал об этом в недавнем видео Numberphile, объясняя, как внутренняя структура купола собора Святого Павла в Лондоне поддерживается перевёрнутой трёхмерной цепной линией.


Цепные линии обладают и ещё одним любопытным свойством. Они являются формой, позволяющей квадратам перемещаться без колебаний их центров (см. анимацию ниже).


Параметризация цепной линии


Если мы хотим научиться рисовать физически точные цепные линии, то (1) может быть не лучшим способом для этого. Причина проста: кроме изменения $a$ у нас практически нет никакого контроля над тем, где и как их можно разместить.

Более «настраиваемым» уравнением является (2), позволяющее перемещать кривую горизонтально и вертикально при помощи двух дополнительных параметров $p$ и $q$:

$$display$$\begin{equation*} y=a \cosh{\left(\frac{x-p}{a}\right)}+q\end{equation*} (2)$$display$$


Однако в идеале нам бы подошло уравнение цепной линии, проходящей через две точки закрепления $P_1$ и $P_2$:

$\begin{split}P_1 & = \left(x_1, y_1\right) \\P_2 & = \left(x_2, y_2\right)\end{split}$


Параметр $p$ позволяет перемещать вершину цепной линии; когда $p=0$, вершина находится на оси Y. Мы можем сдвигать цепную линию так, чтобы вершина находилась ровно между $P_1$ и $P_2$:

$p=\frac{x_1+x_2}{2}$


На самом деле, это идеально, если и $P_1$, и $P_2$ находятся на одном уровне (т.е. когда $y_1=y_2$). Но если это не так, то получившаяся цепная линия будет физически неверной. Кроме того, это почти не позволяет нам управлять степенью провисания цепной линии. Поэтому нам нужно подойти к задаче по-другому: нам нужен более «художественный» способ управления линией.

Решение задачи цепной линии


В этом разделе мы покажем уравнения физически правильной цепной линии, представляющей верёвку, закреплённую в двух точках пространства, $P_1$ и $P_2$, с заданной длиной $l$. Математический вывод уравнения довольно запутан, поэтому чтобы не мучить вас, я просто покажу результат решения.

Для начала зададим два вспомогательных параметра, $h$ и $v$, указывающих горизонтальное и вертикальное расстояние между двумя точками.

$$display$$\begin{equation*}\begin{split}h & = x_2 - x_1 \\v & = y_2 - y_1 \\\end{split}\end{equation*} (3)$$display$$


При выводе уравнения мы предполагаем, что $y_1 < y_2$; если это не так, то можно просто поменять местами две точки. Также нам нужно задать условие, что $l$ больше расстояния между двумя точками. Это кажется справедливым, ведь длина цепной линии должна быть не меньше расстояния между точек закрепления.

Мы получаем следующие значения для $p$ и $q$:

$$display$$\begin{equation*} p=\frac{x_1+x_2-a \ln{\left(\frac{l+v}{l-v}\right)}}{2}\end{equation*} (4)$$display$$


$$display$$\begin{equation*} q=\frac{y_1+y_2-l \coth{\left(\frac{h}{2a}\right)} }{2}\end{equation*} (5)$$display$$


где $\coth$ — гиперболический котангенс:

$coth{x}=\frac{\cosh{x}}{\sinh{x}}$


На показанной ниже анимации (в оригинале статьи она интерактивна) перемещается вторая точка закрепления ($P_2$) и меняется длина цепи ($l$), при этом изменяется форма линии.


Находим a


В предыдущем разделе нам не удалось представить уравнение первого параметра цепной линии: $a$. Так получилось, потому что в этом случае нет лаконичного решения, способного вычислить его точное значение. На самом деле, при любых попытках вывода $a$ мы придём к следующему трансцендентному уравнению:

$$display$$\begin{equation*} \sqrt{l^2-v^2}=2 a \sinh{\left(\frac{h}{2 a}\right)}\end{equation*} (6)$$display$$


Иными словами, мы не можем преобразовать это уравнение в более простой вид $a=...$ так, чтобы $a$ не находилась и в правой части уравнения. Иногда трансцендентные уравнения можно переписать в таком виде, но часто это требует бесконечного количества операций (например, использования рядов или интеграла).

Когда такое происходит, то это значит, что нам нужен другой способ вычисления значения $a$. Если не получается решить задачу аналитически, то приходится использовать численные решения. То есть нам нужно использовать алгоритм для поиска приблизительного решения. Об этом мы поговорим в следующей статье.