
Реакция на опубликованную 12 января 2021 на Хабре работу «Формула решения уравнения 4 степени» свидетельствовала о том, что статья была недостаточно хорошо выстроена методически. Формулы не смогли постоять сами за себя.
Попробую исправить ситуацию.
Итак, уравнение 4 степени.
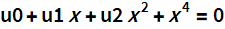
Инстаграм
Сначала о методе Феррари.
Метод Феррари замечателен тем, что он отражает сущность уравнения 4 степени. Выделение полных квадратов приводит к появлению кубической резольвенты. В итоге уравнение можно представить в виде произведения двух квадратных многочленов.
Для уравнения 5 и 6 степени прием, связанный с выделением полных квадратов или кубов, очень быстро заканчивается ничем. Мне кажется, что именно это обстоятельство реально породила тезис о невозможности решения в радикалах уравнений выше 4 степени.
Уравнение резольвенты:
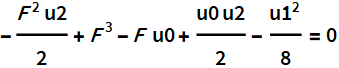
Произведение двух квадратных многочленов, полученных методом Феррари.

Коэффициенты выражения, стоящего в правой части тождества.

Далее подставляем выражение для F^3 из резольвенты и получаем исходный многочлен 4 степени.
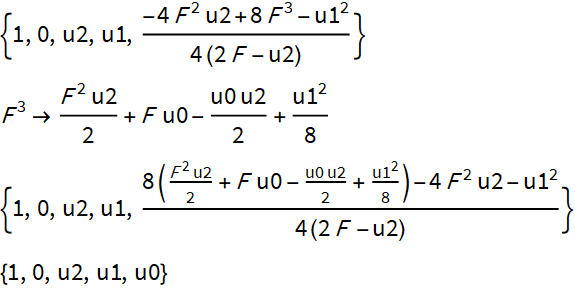
Единственное, что надо отметить, что резольвента проявляется только при вычислении свободного члена.
Корни одного и того же уравнения должны быть тождественны независимо от того, каким методом получены.
На практике в зависимости от использованного метода получаются корни, о которых в их символическом представлении сложно сказать тождественны они или нет. Почему бы не иметь еще один метод решения, который в некоторых случаях дает более простые символические представления корней. Такая возможность важна при подборе значений параметров корней и сопряжении корней нескольких уравнений.
Отличия метода ftvmetrics от метода Феррари:
— другие вспомогательные уравнения (резольвенты);
— вспомогательные уравнения «работают» не на свободном члене, а на коэффициентах при первой и второй степенях;
— есть возможность вычисления двух корней уравнения 4 степени из кубического уравнения, представленного в канонической форме.
Первое решение.
Было приведено в поименованной в начале статье.
Вспомогательное уравнением

Произведение квадратных многочленов, тождественное уравнению 4 степени после неоднократной замены R^3
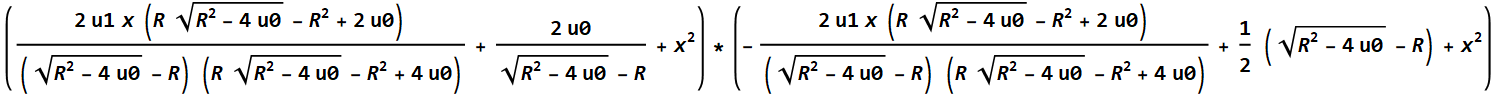
Вместо решения каждого из квадратных многочленов, указанных выше, в методе ftvmetrics можно найти корни кубического уравнения

Два из них будут корнями уравнения 4 степени.
При этом появляется возможность выражения корней через экспоненты или тригонометрические функции.
Убедится в корректности альтернативного уравнения можно, вычислив субрезультанты и проверив два первых значения
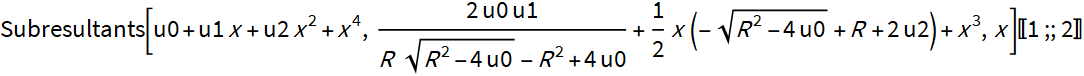
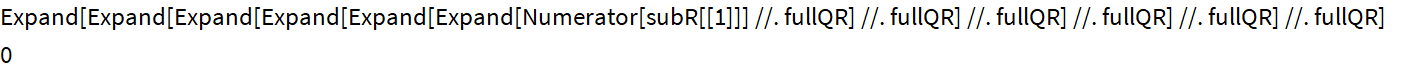

Получаемые выражения субрезультантов «зверские», но когда известно, что ищешь — все не так грустно.
Второе решение.
Вспомогательное уравнение
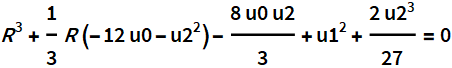
имеет канонический вид.
Произведение квадратных многочленов, тождественное уравнению 4 степени после неоднократной замены R^3

Корректность альтернативного уравнения также проверяется через субрезультанты
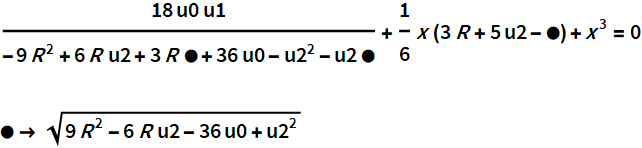
Во втором решении вспомогательное и альтернативное уравнения имеют каноническое представление.
Любопытно получить нечто новое спустя 400 лет.
Интересные задачи бизнеса присылайте в Direct Инстаграм.


anonymous Автор
Извините, но правда не понимаю, что от меня требуется.
Refridgerator
От вас требуется написать интересную статью, раз уж вы взялись публиковать её именно на хабре. А если кому-то потребуется действительно находить корни многочлена — он не будет это делать вручную, а воспользуется мат.пакетом, который ещё и уравнения больших степеней решать умеет (хоть и не все).
anonymous Автор
Статья опубликована в разделе математика. До каких-то пор решение уравнений было главной задачей алгебры. Теорема о наличии такого же как и степень многочлена количества корней была основной теоремой алгебры. Какая сейчас основная теорема я не знаю.
Мат. пакеты находят численное значение корней. В работе рассматриваются символические выражения корней.
Простая задача с матрицей рисков требует решения характеристического полинома. Если Вы хотите поэкспериментировать и зададите риски параметрами, то сразу появятся проблемы нахождения корней — собственных значений.
Неудобства, связанные с решением уравнений с параметрами отбивают охоту с ними связываться. Это приводит к тому, что многие резервы цифрового управления бизнесом не могут реализоваться. Данную ситуацию иногда можно поменять — в этом можно увидеть «интересность» работы.
Refridgerator
Математические пакеты прекрасно находят аналитические решения — в этом-то и их основная ценность. Например.
anonymous Автор
Все, что сделано в двух последних работах — сделано в Wolfram Mathematica. Это система символического программирования. Уверяю Вас, что символические решения уравнений больших степеней делаются через чистые функции, которые содержат информацию в символическом виде о численном решении. Не более того.
Refridgerator
Ну значит вы можете привести пример задачи, с которой не справился Wolfram, но справился ваш метод. Или какое-нибудь очевидное его преимущество.
anonymous Автор
Есть уравнение. У него есть конкретные корни. От применяемого метода значение корней не меняется, а только их представление как алгебраического выражения. Предлагаемый метод позволяет получать более простое алгебраическое представление корней. Соображения почему это так приводятся. Когда надо решить важное уравнение не плохо иметь возможность воспользоваться наиболее ясным из 5 возможных представлений корней. В этом существо предложений.