
Привет, Хабр! Меня зовут Илья Селицер. В DINS мы участвуем в разработке продукта для UCaaS-провайдера RingCentral, который объединяет много функций — от звонков и факса до корпоративного мессенджера и видеоконференций. Я, среди прочего, отвечаю за качество этого сервиса. В повседневной практике мне постоянно приходится анализировать взаимодействие различных сетевых элементов, которые участвуют в предоставлении той или иной услуги абонентам.
Для оценки качества услуги обычно используются отчёты об ошибках, которые формируются на основе сообщений об ошибках от различных сетевых элементов. Анализ достоверности отчётов об ошибках — важный этап оценки качества услуги. В этой статье рассмотрим, как различные статистические методы могут применяться в инженерной практике при оценке достоверности отчётов об ошибках.
Статья будет интересна telco-инженерам и прочим специалистам, которым необходимо проанализировать данные мониторинга, сигнальную нагрузку, качество аудио- и видеовызовов, и другие процессы, представленные в виде временных рядов.
Техническая реализация услуг, предоставляемых UCaaS-провайдером, часто требует сложных архитектурных решений с применением различных видов программного и аппаратного обеспечения. Оценка качества таких услуг может потребовать значительных ресурсов в силу сложности анализа взаимодействия большого количества различных сетевых элементов, участвующих в предоставлении услуги. При этом отсутствие или малое количество заявок от потребителей услуги о проблемах не является главным и единственным показателем ее качества.
Для оценки качества услуги UCaaS-провайдеры могут использовать отчеты об ошибках, формируемые на основе сообщений об ошибках от различных сетевых элементов. Эти отчеты представляются в удобном для анализа виде: таблицы, графики и т.д. Но далеко не всегда по виду таблицы или графика можно сказать, насколько достоверно они отражают процессы, происходящие в сложной многокомпонентной системе. В этом случае для анализа можно использовать различные статистические методы, в частности, анализ временных рядов и тестирование гипотез.
Рассмотрим пример: UCaaS-провайдер предоставляет некоторую услугу S (например, прием факсовых, мультимедийных и прочих сообщений, голосовую почту, запись аудио- или видеозвонка) бизнес-абонентам в нескольких регионах Ri. Процесс предоставления S имеет следующие особенности:
Результат успешного предоставления услуги (SS) — файл Fk некоторого объёма, который сохраняется в течение определённого периода времени в сетевом хранилище. Объём Fk пропорционален размеру сообщения.
Информация о количестве фактов успешного предоставления S для каждого Ri достоверна.
Сетевые элементы NEij, непосредственно участвующие в предоставлении S, генерируют отчёты об ошибках ERj, т.е. о фактах неуспешного предоставления S (SE). Эта информация может быть недостоверной в силу разных причин, таких как ошибки в алгоритме подсчета ошибок, проблемы на уровне ОС, аппаратные проблемы и.т.д.
Отчёт об ошибках по региону SERi формируется для каждого Ri путем суммирования ERj по отчетам от каждого NEij.
Нам нужно оценить, насколько достоверно отчёты SERi отражают реальное количество ошибок, а также спланировать дальнейшие действия в зависимости от результатов оценки. До начала анализа определимся с действиями:
Результаты оценки — «достоверно». Не делаем ничего, т.е. не тратим ресурсы на дальнейший анализ. Оцениваем качество услуги на основе SERi и количества жалоб на качество услуги со стороны абонентов.
Результаты оценки — «недостоверно». Изменяем механизм формирования ERj. Это весьма ресурсоемкая задача, так как потребуется не только дополнительный анализ сценариев взаимодействия, но, возможно, доработка сетевых элементов и даже изменение архитектуры предоставления S.
На основе данных о технологии оказания той или иной услуги, а также результатов наблюдения за системой, можно сделать следующие предположения:
Потребление S растёт со временем. Это обусловлено, например, ростом абонентской базы и/или растущим спросом на S.
Количество запросов на предоставление S изменяется с некоторой периодичностью, характерной для бизнес-пользователей, например, рабочие дни-выходные.
Количество SE растет с ростом потребления, т.е. количества фактов успешного оказания услуги, например, из-за перегрузки сетевых элементов.
Количество SE растет с ростом среднего объёма Fk. Например, количество ошибок при приёме факсового сообщения вырастет с ростом размера принимаемых факсовых сообщений (и, соответственно, объёма файлов Fk): приём 10-страничного факса потребует больше времени, чем 1-страничного, вероятность возникновения ошибки при приёме увеличивается с ростом времени приёма при прочих равных условиях. Следовательно, число ошибок при приёме большого количества 10-страничных факсов будет больше, чем при приёме такого же количества 1-страничных.
Исходя из утверждений 1-4, а также учитывая, что зависимости SS и SE от времени суть временные ряды (time series, TS), используем следующие возможные результаты анализа TS SE (TSE), по которым будем определять степень достоверности информации, предоставляемой отчётами об ошибках:
TSE стационарен, т.е. не имеет сезонности и тренда.
TSE нестационарен, т.е. демонстрирует сезонность (seasonality) и тренд (trend) — это и будет принято в качестве критерия достоверности данных, предоставляемый TSE.
Нестационарный TS может и не иметь тренда, один из примеров — случайное блуждание (random walk, RW), хотя этот факт применительно к RW, в некоторых случаях, подлежит обсуждению.
В качестве инструментов анализа будем использовать различные методы тестирования стационарности TS, а также оценку автокорреляции TS (ACF). Используем TSS и TSE для одного из регионов, полученные на реальной сети UCaaS-провайдера. Для анализа используем Python и соответствующие статистические и графические библиотеки. Код доступен здесь, для просмотра кода и графиков можно использовать nbviewer.
TSS
Сначала проанализируем TSS. Построим графики TSS и декомпозиции TSS, коррелограмму — рис. 1-3. Для декомпозиции использованы следующие значения параметров:
model = ‘multiplicative’. Мы рассматриваем TSS как произведение трёх компонент: тренда, сезонных колебаний и случайной величины (остаток, residuals) [1]. На мультипликативную модель указывает, например, возрастающий со временем размах сезонных колебаний.
period = 7 (period = ‘None’ даст тот же результат).



Анализ графиков на рис. 1-3 приводит к следующим выводам:
Сезонность чётко различима и равна 7 дням (рис.1).
Присутствует положительный тренд (рис. 2). Это случай детерминированного тренда: несмотря на скачкообразные изменения значений тренда, его наклон (slope coefficient) возвращается к исходному значению на более длительном отрезке времени.
Величина автокорреляции уменьшается с ростом лага. Это обусловлено трендом, тогда как форма, напоминающая затухающую синусоиду, — это следствие сезонности. В нашем случае корреляция между значениями TSS в момент t максимальна в момент t ± n*7 дней, n = 1 … 5. Закрашенная область на рис. 3 — это доверительный интервал (confidence interval, CI) для ACF. Значения ACF, попадающие за пределы этой области, статистически значимы.
Наличие сезонности и тренда говорит о нестационарности TSS [1]. Проверим TSS на стационарность с помощью ADF-теста (Augmented Dickey-Fuller). ADF-тест в качестве нулевой гипотезы (H0) постулирует наличие единичного корня [2, 3], что указывает на нестационарность TS. При этом отсутствие единичного корня не говорит о стационарности TS. Получаем следующие результаты:

p-value > 0.05, результат не является статистически значимым, H0 не может быть отвергнута.
Как и предполагалось до начала анализа, TSS нестационарен, что подтверждается собственно графиком процесса, результатами декомпозиции, коррелограммой, ADF-тестом.
Объём Fk
Как указано выше, размер сообщений пропорционален объёму Fk. Оценим, как меняются значения Fk со временем. Гистограмма с линейным масштабом Fk — см. рис. 4, с логарифмическим масштабом — см. рис. 5, коробчатая диаграмма (box plot) — см. рис. 6.


Некоторые выводы по рис. 4, 5:
Распределение несимметрично, присутствует правый хвост (right-skewed).
Среди значений объёма Fk присутствуют экстремальные значения/выбросы (outliers).
Среди экстремальных значений присутствуют нулевые значения, являющиеся результатом округления Fk в меньшую сторону.

Коробчатая диаграмма на риc. 6 показывает, что:
Количество экстремальных значений Fk > 55 заметно уменьшилось;
Медиана несколько выросла, несмотря на колебания от месяца к месяцу;
Характер распределения Fk примерно одинаков от месяца к месяцу. Средние, медианные и максимальные значения Fk по месяцам:

Несмотря на некоторые колебания, медиана Fk растёт со временем, количество экстремальных значений изменяется в сравнительно небольших пределах. Более детальное изучение распределения Fk также необходимо для понимания особенностей использования S потребителями и является предметом отдельного исследования.
Информация, представленная в виде графиков на рис. 1-6, в значительной степени совпадает с предположениями 1-4.
TSE
Построим TSE и попытаемся обнаружить и оценить особенности этого графика.

График на рис. 7 не показывает явно выраженную сезонность, также присутствуют нулевые значения SE.
Проведём декомпозицию TSE — см. рис. 8. Параметр model=“additive” т.к. в TSE присутствуют нулевые значения, period = “None”.

Декомпозиция TSE указывает на сезонность с периодом 7 дней, а также на отсутствие выраженного тренда.

Коррелограмма на рис. 9 также не показывает сезонность, как в случае TSS: всего два значения статистически значимы, остальные значения статистически незначимы. В то время как декомпозиция TSE указывает на наличие сезонности TSE с периодом 7 дней, коррелограмма TSE не показывает заметной автокорреляции с лагом, кратным 7 (рис. 9). Тот факт, что используемый для данного случая алгоритм декомпозиции обнаружил сезонную компоненту, не означает, что сезонность присутствует или существенно определяет свойства TSE: даже для RW этот алгоритм декомпозиции обнаруживает сезонную компоненту. В этом случае необходимо использовать другие доступные методы оценки стационарности TSE.
ADF-тест даёт следующие результаты:
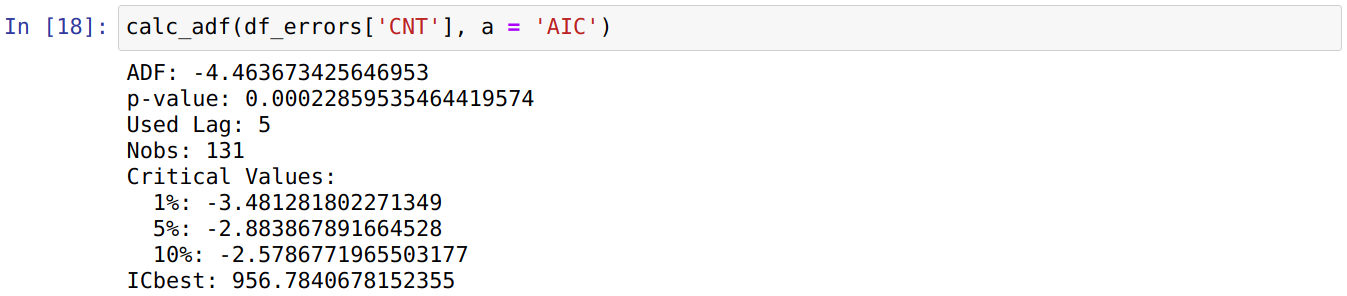
Значение p-value << 0.05, результат статистически значим, принимаем альтернативную гипотезу (H1): TSE стационарен. Для более надежной проверки, в дополнение к ADF-тесту используем KPSS-тест (Kwiatkowski-Phillips-Schmidt-Shin). В отличие от ADF-теста, KPSS-тест постулирует в качестве H0 стационарность процесса, а в качестве H1 — наличие единичного корня. ADF- и KPSS-тестам свойственны некоторые недостатки, например, высокий уровень ошибок первого рода (ошибочное отвержение H0), однако совместное применение ADF- и KPSS-тестов позволит уменьшить влияние этих недостатков на результаты анализа TSE [3].
KPSS-тест даёт следующие результаты:

Здесь p-value > 0.05, т.е. не является статистически значимым, принимаем H0: TSE стационарен.
Приходим к следующим выводам:
На основании анализа коррелограммы TSE, а также ADF- и KPSS-тестов, считаем, что TSE стационарен.
Стационарность TSE говорит о том, что данные в отчетах об ошибках не соответствуют нашим представлениям о системе, т.е. наблюдаемому поведению системы.
Механизм формирования отчётов об ошибках нуждается в более детальном исследовании и последующей корректировке.
Заключение
Применение различных статистических методов анализа временных рядов позволяет более точно оценить характеристики сложной многокомпонентной системы, предоставляющей данные для построения этих рядов. Ни один из этих методов не позволяет вычислить с достаточной точностью все характеристики временных рядов, поэтому для повышения информативности анализа необходимо совместное применение нескольких разных методов анализа.
Вопросы или комментарии читателей, возникшие по прочтении данной статьи, приветствуются.


tvant
Я чего-то не уловил. Взяли некий длинный по времени отчёт(ы) и покрутили его в Phyton (хотя в R такое делать удобнее). Увидели некие тренды и периодичность (сезонность). Сочли, что это мешает нам видеть истинное распределение ошибок. Убрали помеху. Что видим? Оказывается некие отчеты об ошибках не согласованы с «чистым» распределением. После этого предлагается поковыряться в отчетном механизме.
И тут у меня вопрос. А где работа с проверкой временного ряда. Как сводились шкалы отсчётов? Как контролировались и компенсировались пропуски значений? А не являются ли выбросы значений в реальности пропуском? Ну и прочая математическая статистика, присущая временным рядам.
Так и бывает, кто-то в подрядчиках/вендорах/поддержке изучит модную штуку на Питоне и брякнет менеджерам «мол там есть ошибки, я это по пи-валуе вижу», а потом телком инженеры делают тотальный аудит настроек оборудования пороги/уровни/адреса/критерии у нормально и бесперебойно работающего оборудования.