Привет, Хабр!
Вспоминая свои программы, которые я делал во времена обучения в вузе, решил поделиться ими с Вами. Насколько я припоминаю, их делал на занятиях по графике.
В чем их отличие от тех, которые я Вам представлю, они были написаны на Delphi. Конечно время идет и прогресс не стоит на месте, в том числе и мои навыки в новых инструментах разработки.
Теперь перейдем к сути статьи.
На википедии есть страница с их списком.
Насколько я знаю ими занимались различные известные и не очень математики. Часть из них я смог реализовать в программах на webgl. Это будет экспериментальная статья, так что прошу любить и жаловать. Рассмотрим 5 примеров алгебраических кривых разных порядков.
Гиперболическая спираль

Параметрическая запись:
https://codepen.io/Gremlin_Rage/pen/zYzOwoB
Чем то похоже на окружность, но с увеличением t, увеличивается радиус окружности.
Кардиоида

https://codepen.io/Gremlin_Rage/pen/powzPez
Астроида

https://codepen.io/Gremlin_Rage/pen/QWgLvvX
Лемниската Бернулли или бесконечность

https://codepen.io/Gremlin_Rage/pen/abwoWLJ
Дельтоида
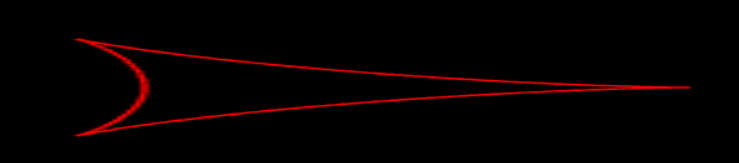
https://codepen.io/Gremlin_Rage/pen/dyRbWmd
Дельтоида получилась не такая, как на вики, так что если есть вопросы по формуле, оставьте замечание в комментариях. На самом деле почти нечего сказать по данной теме, я лишь пытаюсь популяризовать сам предмет, не в частности этот.
Спасибо за понимание!
Комментарии (17)

Naf2000
29.08.2021 07:24

belch84
29.08.2021 14:24Было бы очень очень интересно посмотреть на решение той же задачи в Вашем приложении.
Это несложно, только спектр находится непосредственно, без импульсных характеристикКраевая задача для уравнения МатьёПоказано решение задачи на собственные значения для уравнения Матьё с нулевыми краевыми условиями на интервале. Видно, что, как и полагается для всякой задачи Штурма-Лиувилля, собственные значения при увеличении своего номера n ведут себя как n^2, а собственные функции имеют перемежающиеся нули (т.е. нули следующей по порядку собственной функции лежат между нулями предыдущей)

Скажу сразу, что моё приложение умеет решать краевые задачи только для уравнений/систем второго порядка. Изображение мелковато, но это связано только с особенностями отображения в Хабре, у меня есть более крупный вариант.
А пример работы вашего приложения с пояснениями можно будет увидеть?
Refridgerator
29.08.2021 17:57Я не увидел ничего общего между своим решением и Вашим — но конечно же только потому, что недостаточно хорошо разбираюсь в решении дифференциальных уравнений. У меня рассматривалось распространение волны внутри сферы, и задачей анимации было показать, что стоячие волны в ней тоже образуются, вопреки представлениям некоторых аудиофилов. Также рассматривалась интерференционная картина на отдельно взятых частотах,
в частности



belch84
29.08.2021 18:08Я не увидел ничего общего между своим решением и Вашим — но конечно же только потому, что недостаточно хорошо разбираюсь в решении дифференциальных уравнений
А что может быть общего, вы же не выписали, решением какого точно уравнения вы занимаетесь. Уравнение Матьё — вполне себе известное, мои решения можно перепроверить
Refridgerator
29.08.2021 18:15Ну Вы наверное должны понимать, что уравнение Матьё и ему подобные — это сильно упрощённые модели (как минимум потому что оно одномерное) для того, чтобы их можно было решить аналитически и были придуманы тогда, когда численные решения были просто невозможны, в отличие от сегодня.

belch84
29.08.2021 18:34Ну Вы наверное должны понимать, что уравнение Матьё и ему подобные — это сильно упрощённые модели (как минимум потому что оно одномерное) для того, чтобы их можно было решить аналитически и были придуманы тогда, когда численные решения были просто невозможны, в отличие от сегодня.
Вы же понимаете, чтоуравнениямодели не придумывают, они возникают естественным образом из задач (в данном случае физических). Кстати, именно уравнение Матьё — оно простое-простое, но им описывается интересное явление — параметрический резонанс, при котором неограниченное возрастание решения происходит не при дискретных значениях параметра, а в целом континууме (диапазоне) его значений, и это имеет вполне себе практические применения
Refridgerator
29.08.2021 18:59Понимаю именно как «придумывают», потому что модель по определению является упрощением описываемого ею явления, и автор модели сам определяет, какие упрощения допустимы, а какие нет. В частности, мат. модель катапульты сильно зависит от того, учитывать ли сопротивление воздуха, ветер, неравномерность g, неравномерность поверхности земли и прочее, и в простейшем случае представляет даже не параболу, а дугу окружности. То же волновое уравнение более точно считается на гексагональной сетке — но там сложнее подавление волн на краях реализовывать, а в 3d так и тем более.






belch84
Подброшу и своих кривых немного
Refridgerator
А почему «своих»-то? Давно известные кривые. А нарисовать можно было и покрасивее — антиалиасинг же давно придумали.
belch84
Своих потому, что нарисованы они в моем собственном приложении. Покрасивее нарисовать можно, но я могу их нарисовать достаточно быстро, а также анимировать, нарисовать трехмерные кривые и расмотреть их с разных сторон, для этого приходится антиалиасингом пожертвовать (и жертвую я несколько меньше, чем автор). Еще могу нарисовать поверхности, и все это без программирования, только задавая формулы
Эта поверхность тоже не моя, я её только изображаю и анимирую
Refridgerator
Так миллион таких приложений)
belch84
Моё приложение несколько отличается от миллиона остальных, поскольку оно умеет решать дифференциальные уравнения и анимировать изображения трехмерных фазовых траекторий (собственно, это его основная функция, кривые, поверхности и прочее — побочные)
Записи в GIF у меня нет тоже, я пользуюсь Гифмэйкером
Refridgerator
Нет конечно, мой комментарий был строго по заявленной теме статьи. Просто на хабре хочется видеть материал уровня чуть выше школьного (хотя бы).
И краевые условия считаются, и импульсную характеристику можно снять, чтобы её в спектр потом разложить.
belch84
Не вполне понял, вы имеете в виду, что пропагандируемое вами ПО умеет решать краевые задачи?Это из комментов к приведенному вами видео на Youtube. Если вы автор этого ПО, то мне кажется, диапазон его применения несколько узковат. Моё приложение может решать любые дифференциальные уравнения (обыкновенные, ну, не более чем 25 порядка, есть и другие ограничения), и представлять результаты решения в наглядном виде, включая всякие тонкости вроде точек сечений Пуанкаре и графиков зависимостей показателей Ляпунова от параметров для произвольной системы. Если вы полагаете, что ваше ПО проделает исследование диффуравнений лучше — я возражать не собираюсь, но у меня впечатление, что оно не очень универсально. Моё же приложение подойдет даже для использования школьником, интерересующимся тем, что такое динамические системы. И еще, его можно скачать и попробовать, ваше, надеюсь, тоже можно?
Refridgerator
Конечно узковат, потому что решает одну конкретную задачу — но делает эту лучше, чем универсальные решатели. Какой вообще смысл решать уравнения без понимания их смысла? Здесь я сделал то, чего не нашёл в других реализациях, в частности, настраиваемый PML.
Было бы очень очень интересно посмотреть на решение той же задачи в Вашем приложении.
Моё нельзя, потому что оно никому не нужно и я не вижу смысла тратить кучу усилий на описание что к чему и зачем, на продвижение и сопровождение. Но может быть, когда нибудь напишу статью на хабре об этом вот всём.
А parametric surface creator скачать можно с неофициальных источников например здесь.
APrioriAPosteriori
Четырехкрылый?? Помнится в аспирантуре в годы труда в нейробиол. лабе (comp. neuroscience) и двухкрылый вызывал панику (еще надо было в домашке это 2Д чертить, учили бы нас вот такой визуализации!)
Если есть гифки с визуальным оформлением чуток поинтересней (в плане цветовой гаммы), можно начинать аккаунт на giphy, собирать единомышленников, там встречаются!
Конкретный вопрос от дилетанта:
в смысле три фазы по траектории представлены в гифке направлением(ями) ротации по разным плоскостям(грубо говоря). Я прямо пригипнотизировалась на эти ротации, т.е. пытаюсь понять, как порядок направлений (и сами направления) ротации решаются при создании визуализации?
belch84
Фазовая траектория — это траектория, которая описывает изменение динамической системы в фазовом пространстве. Если динамическая система представляется в виде системы трех дифференциальных уравнений
 ,
,
то её изменение с течением времени можно представлять как три разных графика x(t), y(t), z(t), а можно — как график одной трехмерной кривой, начинающейся в точке (x0,y0,z0). Система уравнений для четырехкрылого аттрактора взята из работы
https://www.scielo.br/j/bjp/a/PZsxkWyBdyDpS3sHTQVwKZq/?lang=en&format=pdf
В этой книге описаны методы построения аттракторов с множеством «крыльев»
http://www.ee.cityu.edu.hk/~gchen/pdf/LC-IJBC06-survey.pdf