
Привет, Хабр!
Сегодня поговорим о примерах в дисциплине уравнения математической физики общими словами без погружения в сухой, академический язык и множества формул.
По шкале сложности для чистой математики эта дисциплина на мой субъективный взгляд получает 7/10. Но это не значит, что эти формулы легки для зазубривания и запоминания. Тем более говорить о том, что я могу сделать открытие в данной области которое попадет в учебники, например объясняя физику какого - либо нового процесса или уточняя уже существующий. Если подумать, то, например выбирая какой-либо параграф учебника по данному предмету, то он исписан формулами, которые если провести аналогию похож на модуль по программированию. Скажу сразу мне преподавали данный предмет очень плохо, не объясняя, что данные формулы значат, точнее заглавие было например: "Уравнение волны" или "Колебание мембраны", а дальше переписывали все формулы в параграфе с короткими комментариями что откуда, весьма скудными в полной тишине. Препод перелистывал страницы презентации и ходил туда-обратно пока мы переписывали. Видно, что не ему, ни мне это было не нужно, как бы для общего развития. Скорее всего надо было читать дополнительную литературу чтобы понять, но там уровень для подкованного студента, предметов было много и где-то были пробелы и особо не было времени на все распылиться. Ну это так, к слову. К слову, чем больше людей надо учить в промежутке времени, тем меньше времени уделяется каждому студенту и тем хуже уровень знаний у каждого студента, ну это в пределе.
Ну это было уже давно, лекций не осталось, практика забылась, из головы все выветрилось как талая вода. Вот пример волны наглядный:

https://codepen.io/Gremlin_Rage/pen/eYWBeNY
Как бы это уравнение бегущей волны с незакрепленными концами. Я мало что знаю об волнах, даже на уровне физики школьного курса, что-то типа амплитуды, периода, волнового числа и всего такого. Волны бывают продольные, поперечные, сферические, спиральные и другие. Это я только что прочитал на википедии.
Данный код ниже представляет практический интерес.
function fi(x)
{
return Math.sin(15*x);
}
function ksi(x)
{
return Math.cos(18*x);
}Как видите есть две функции, ksi и fi, они заданы тригонометрическими функциями sin, cos. Они характеризуют нашу волну. Там же есть аргументы функций 15*x и 18*x. Если, например увеличивать число 15 или число 18, то количество холмов будет увеличиваться, по-умному это значит, что чем большее число мы впишем в скобки, тем самым мы увеличиваем количество периодов функций данных, которые уместятся в заданный промежуток числа x. При увеличении будет сжиматься график вдоль оси Ox.
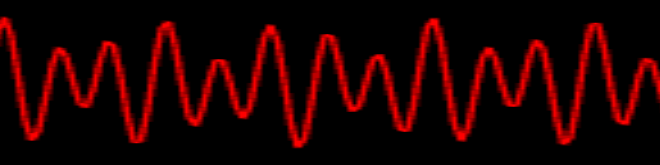
Икс то мы не увеличивали, шаг остался тем же около 0.01. Если мы будем уменьшать данные аргументы, то количество полных периодов функций будет меньше и как бы график растянется вдоль оси Ox.

function fi(x)
{
return 15*Math.sin(x);
}
function ksi(x)
{
return 0.8*Math.cos(x);
}А если мы вынесем за скобки и будем увеличивать/уменьшать само значение функции, как на коде выше, то будет растягиваться/сжиматься вдоль оси ординат, то есть вдоль оси Oy. Что показано на графиках ниже.

Здесь растяжение настолько большое что не вмещается в рабочее пространство и надо увеличивать рабочее пространство сцены и отдалять наблюдательное око.
А ниже наоборот сжатие относительно оси ординат.

Дело в том, я вот заметил, что каждое объяснение волн очень сложное, трудно выстроить в голове какие-либо упорядоченные знания об этом. Но я решил, что буду заниматься теперь только самыми насущными вещами, а не чтением гуманитарных статеек в интернете. Я очень много времени потратил на безделье и чтение всяких новостей, я превратился в гуманитария и не заметил.
С другой стороны, а как реализовать эти знания и монетизировать их? Не думаю, что есть вакансии, с требованием к программисту рисовать волны в браузере.
А вот второй пример посложнее, где уравнение окружность:
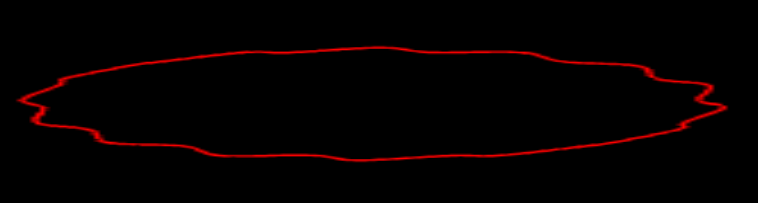
https://codepen.io/Gremlin_Rage/pen/gOWwerd
Хотелось сделать такой круг с волнами в виде, который похож на ютубе видел, как анимация голосовых волн от микрофона, но не получилось.
Здесь также можно увеличивать аргумент или/и значение функции и будет весьма интересно просмотреть результат.
Перейдем к следующему примеру, это концентрические окружности с волновым движением по оси Y:

https://codepen.io/Gremlin_Rage/pen/OJmvmEg
Чем-то похоже на изделие №1. Тот же принцип, но уже по массиву колец изменяется график, все кольцо увеличивается и уменьшается на одно значение, а другое кольцо уже на другое.
Чтобы улучшить вид, надо уменьшить шаг до тысячной доли, увеличить размер массива vertices в 10 раз, тогда не будет видно разрезов и будет идеально.

Это вид сбоку.
Резюмируя, хочу сказать вот многие говорили: "Зачем эти синусы и косинусы нужны?"
Вот для этого и многих других вещей, я, например написал об этом здесь, кто-то еще что-то придумает получше. Хотя трудно найти веб-программиста-математика-физика-художника, адская смесь получается.
Да, статья получилась не особо научной и в некотором роде объективной, но надо было чем-то заполнить пространство между картинками, спасибо у меня все!
Комментарии (16)

Tiriet
24.08.2021 17:07+5мдя. уравнения математической физики. В приличном обществе- уравнения математической физики начинаются с постановки задач физики, которые этими уравнениями решаются. Какое отношение Ваши косинусы и синусы имеют к физике? А самое элементарное, эти косинусы и синусы являются собственными решениями дифференциальных уравнений, описывающих колебания струны или всяко-разно закрепленной упругой балки.
По идее, после этого идет рассмотрение распространения волны в бесконечной упругой струне- там получается простое решение в виде двух разбегающихся волн той же формы, что и начальное возмущение. Затем- переходим к решению задачи теплопроводности- узнаем про уравнение Лапласа, решаем его в одномерном стержне- узнаем про существование эрфекта и всякие интегральные свертки, которые с ним можно сделать, затем- переходим на следующий уровень- теплопроводность в двумерной и трехмерной постановке- пробуем простейшие осесимметричные задачи (типа нагрев цилиндра и остывание шара)- узнаем про функции Бесселя. Потом в лобешник получаем задачей Штурма-Лиувилля, из глаз фонтаном сыплются собственные функции дифференциальных операторов, башку распирает функция Грина, влезаем в гидродинамику- где нас вихрем нахлобучивает от тензорного анализа и разрывных решений для сжимаемой жидкости с нелинейным уравнением состояния. Ну а потом- уже по специализации- какие-то скучные прикладные задачи из какой-нибудь очень интересной перспективной мутотени. И тут Вы, с косинусом и без уравнений. ээээх, ностальгия!

klvov
24.08.2021 22:08Нда, вспомнилось, как нас в старших классах школы "троллили", извините за такое слово, на физических олимпиадах задачками вроде "насколько быстрее сварится яйцо курицы, чем яйцо страуса". Я пытался что-то сообразить в качестве решения, но получалась какая-то ерунда, потому что даже представления о реальной сложности задачи не имел, а для того, чтобы даже подступиться к ее решению, нужно, в худшем случае, представление о вот этом математическом аппарате хотя бы иметь, а, по-хорошему, им более или менее владеть. А у нас в 10-м классе был в загашнике, ну, закон Гука. И то, что этот закон можно как-то переформулировать для решения задачи "о двух яйцах", в то время догадаться было невозможно.

GospodinKolhoznik
25.08.2021 00:37+2А чего тролли то? Хорошая задача. Уравнения изменения температуры со временем будут оди и те же, что для яйца курицы, что страуса. Значит и решать их не надо, а надо найти только зависимость между временем и расстоянием прогрева.
Уравнение dT/dt = d2T/dx^2 выводится не сложно, а решать его не надо, надо лишь заметить, что если в нем не изменяя температуру изменить расстояние x в n раз, то время t изменится в n^2.

Tiriet
25.08.2021 06:13+1так потому и "олимпиадные задачки"- есть занудное неподьемное решение "в лоб", а есть- быстрое красивое решение в обход, но его надо сообразить.
до сих пор помню задачу- есть три окружности А, В, С разных радиусов, есть две общих касательных к окружностям А и В, есть две общих касательных к окружностям В и С, и есть две общих касательных к окружностям А и С. при этом, точки пересечения касательных не лежат между центрами окружностей. и надо доказать, что точки пересечения касательных лежат на одной прямой. Так вот нудное решение- крайне нудное, листов на пять формул и рисунков, а красивое строилось на том, что если эти окружности надуть в сферы с такими же радиусами, и на эти сферы сверху и снизу положить две плоскости- то плоскости лягут ровно и пересекутся строго по одной прямой, а значит, если на этих сферах нарисовать конусы- то вершины этих конусов будут тоже лежать на этой прямой, а так как касательные наши являются направляющими этих конусов- то их точки пересечения есть вершины конусов и потому- лежат на прямой пересечения наших плоскостей: доказательство- одна кривая картинка и три строчки текста.

klvov
25.08.2021 22:09Задача действительно хорошая, и решение, которое нам в конце концов показали, было, вроде бы, именно таким, хотя 20+ лет прошло, могу помнить неточно. Что яйцо курицы и страуса (округленное до "сферического яйца в вакууме") будучи помещенным в кипяток, нагревается по одним и тем же законам, это мы дотумкали. Что время, нужное на прогрев "яиц" разного размера будет разным - тоже интуитивно понятно, стоит представить себе "яйца" диаметром в 1 миллиметр и в 1 метр, помещенные в "кипяток". Что количество тепла, поступающее в "яйцо", будет линейно пропорционально площади его поверхности - тоже было понятно. Но вот уравнение вывести скиллов тогда не хватило, у нас был обычный (не физмат) класс, и диффуры мельком нам показывали уже сильно потом, на втором курсе, и то не сильно требовали заучивать, потому что скорее всего "не пригодится".

GospodinKolhoznik
24.08.2021 23:59На противогаз совсем непохоже.

vesper-bot
25.08.2021 09:35Изделие №1 — это колпачок на шейку матки, а не противогаз. Но я узнал об этом менее года назад.

belch84
26.08.2021 13:12Вот, нарисовал и анимировал нечто, похожее на ваше изделие, своими средствами
МембранаВообще, мне кажется, что Web-программирование тут ни при чём, анимированные изображения удобнее создавать традиционными средствами, вроде Wolfram Mathematica, или Matlab, или даже с помощью моего собственного скромного приложения (программирования для мембраны не потребовалось, только задание формул и соединение отдельных кадров в анимацию), а затем вставлять в нужные страницы в виде анимированных изображений или видео.
То, что вы пытаетесь построить — это проволочные модели, их тоже удобно генерировать и просматривать с помощью внешних специальных средств, не требующих Web-программирования
Travisw Автор
26.08.2021 20:223дорово смотрится, но ты же не сможешь установить вольфрам и матлаб в смартфон и открыть анимацию в брау3ере. Но это мелочи. Да сложно писать на вебжл надо думать про всякие программистские вещи вроде выделения памяти и прочего, а в матпакетах проще в этом плане, но я слабо 3наю матпакеты. И теорию тоже, мне в матпакетах особо делать нечего.

belch84
26.08.2021 20:55Создавать анимации в телефоне достаточно неудобно, это все равно, что редактировать в телефоне сложные документы — это возможно, конечно, но можно будет одуреть после одного полного рабчего дня. С браузером дело обстоит лучше, Matlab, например, существует в виде браузерной версии, но она мало чем отличается от десктопной. В любом случае, удобно реализовать создание анимаций в достаточно общем виде, а не писАть для каждого изображения программу. В таких программах будет довольно много повторяющихся фрагментов. Но мне кажется, что создавать такой универсальный инструмент при помощи Web-программирования сложнее (о выделении/освобождении памяти придется думать в любом случае)

Travisw Автор
26.08.2021 22:23Вот и3-3а того, что инструмент 3аточен под программирование , а не под математику, приходится сосредотачиваться и думать не об том, что хотел. Это отнимает время, устаёшь. А вот например в3ять тот же матлаб - напечатал выборку и3 нормального распределения, потом преобра3ование фурье сделал, потом нейросетью распо3нал потом с анали3ировал нашел автоколлиряцию, увидел 3акономерности и нашел применение в какой - нибудь практической области и даже не 3наю что еще можно, сделать и т.д. и т.п. То есть вложенная компо3иция функций. Насколько хватит полёта мысли? Кто 3нает, и получится во.

Refridgerator
28.08.2021 21:13Сначала я подумал, что это какой-то толстый троллинг. Однако рейтинг и у статьи, и у автора по итогу недели внезапно положительный. Ну ок, походу проблема во мне. Как минимум, спасибо за перл:)
Волны бывают продольные, поперечные, сферические, спиральные и другие. Это я только что прочитал на википедии.



Javian
В свое время впечатляла демка Марс.
Mars DOS demo by Tim Clarke (1993)
ciubotaru
В Excel 97 была пасхалка с подобным.
Javian
В 97 несколько другое
Excel 97 Easter Egg
olegshutov
Я помню мы, школьниками, ее запустили. Думаем - красиво. А потом нам подсказывают мышкой подергать и мы такие - оооо! тут еще и ездить можно! Я смотрел исходники, там ассемблер и причем полностью развернутый цикл копирования из буфера на экран попиксельно :)