Доброго времени суток, хабровчане! Сейчас я попробую окунуть вас в интересное, всеми забытое, где-то немного сложное дерево PATRICIA, также реализую ее на языке С++, будет очень больно, приготовьтесь.

Немного теории и сразу начнем с реализации

Патриция представляет собой смешение trie и DST дерева, на ней можно написать свой собственный ассоциативный контейнер, используется чаще всего для сравнения строк, а переход между вершинами происходит по сравнению соответствующего бита.

Каждая вершина имеет:

1. Ключ(string key)

2. Значение(int value)

3. Индекс бита, который нужно проверять для поиска(size_t index)

4. Указатели на правую и левую вершину(Node *right, *left)

struct Patricia::Node{
    std::string key;
    int value;
    size_t index;
    Node *right, *left;

    Node(const std::string& key, const int& value, const int& index)
        : key(key), value(value), index(index), left(nullptr), right(nullptr) { }

    ~Node(){}
};

Теперь самое время поговорить о самой патриции, а точнее о ее свойствах, их немного. Во-первых, правый указатель корня - nullptr всегда. Во-вторых, каждая вершина патриции, кроме корня имеет ненулевой индекс, и все указатели всегда направлены на другие вершины, поэтому каждый метод дерева в самом начале проверяет существование корня, а поиск начинается с левой вершины от корня. В-третьих, листом считается вершина, один из указателей которого направлен на самого себя. На данный момент интерфейс патриции выглядит так:

typedef class Patricia{
private:
    struct Node;
    Node *root = nullptr;
public:
} patr;

Пример визуализированной патриции (для упрощения я не стал рисовать value вершин):

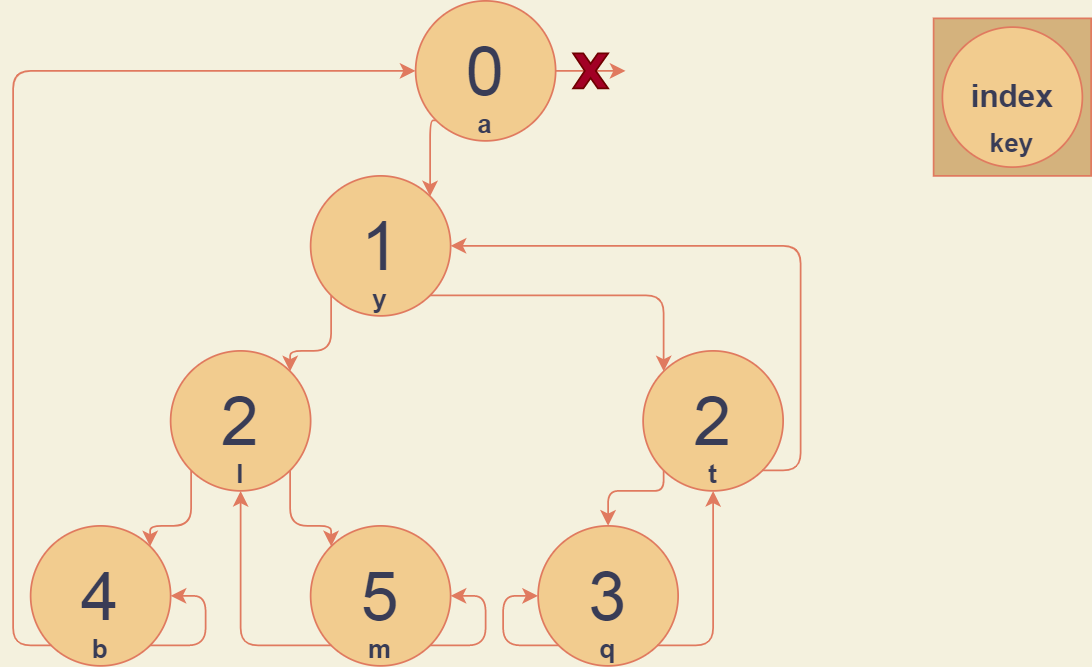
Немного разберемся в примере, справа сверху нарисован шаблон, в котором указано, что обозначается. В нашем случае, в центре пишется индекс бита, который мы должны проверять, находясь в этой вершине. Внизу пишется сам ключ. Теперь попробуем реализовать функцию поиска вершины в нашем примере дерева(1).

Сделаем ограничение на алфавит в нашем ключе, использовать можно только латинские буквы в нижнем регистре. Теперь можно вывести на экран битовое представление каждой латинской буквы, нам это понадобится(советую продублировать вкладку).

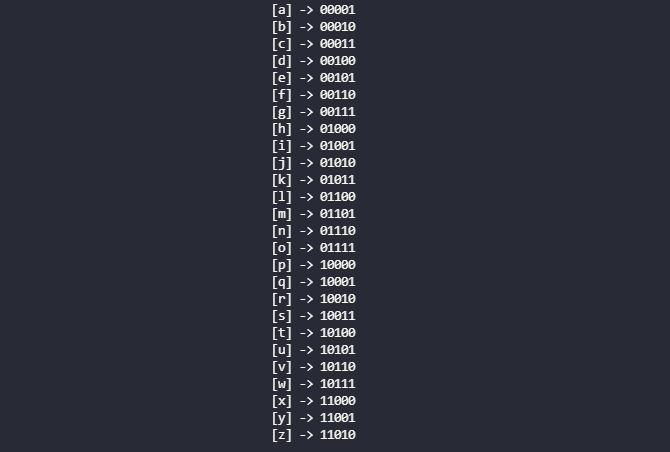
Поиск

Попробуем найти узел с ключом "a", его побитовая цепочка 00001. Важно заметить, что индекс идет не с 0, а с 1, таким образом '1' будет иметь индекс 5.

Как было сказано выше, мы проверяем существование корня, если его нет, то выводим nullptr, если есть, то начинаем поиск с левого узла, в примере это узел с индексом 1 и ключом "y". Берем текущий индекс и проверяем бит из искомой побитовой цепочки в позиции текущего индекса. В данном случае бит равен - 0, поэтому мы двигаемся по левому указателю.

Теперь текущий узел равен индексу 2 и ключу "l", проверяем бит из исходного ключа("а") по текущему индексу(2). Бит равен - 0, поэтому снова двигаемся по левому указателю.

Теперь текущий узел равен индексу 4 и ключу "b", проверяем бит из исходного ключа("а") по текущему индексу(4). Бит равен - 0, поэтому снова двигаемся по левому указателю.

Поиск заканчивается тогда, когда индекс текущего узла меньше или равен предыдущему, текущий индекс - 0, предыдущий - 4. Поиск закончен, найденная вершина: "а", индекс 0 - является нужной нам вершиной, которую мы искали.

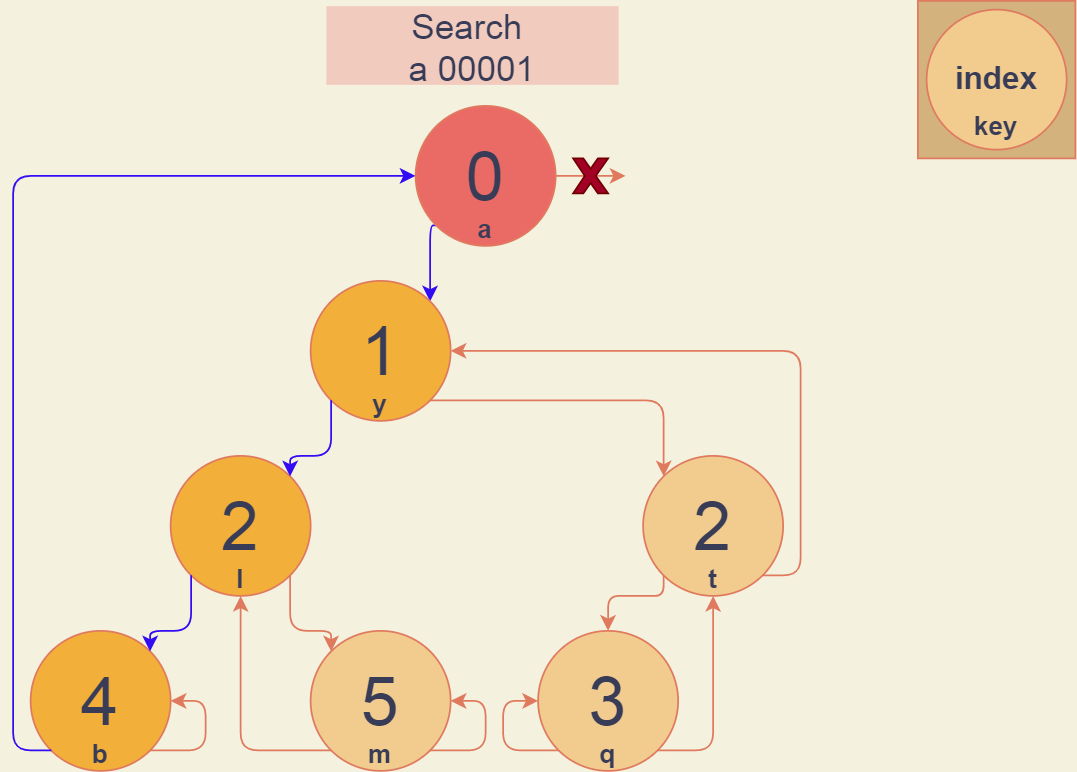
Давайте напишем метод Search. Во-первых, создаем два указателя currentNode и prevNode, они нужны для отслеживания текущей вершины и выхода из функции, осуществляется когда currentNode->index <= prevNode->index.

Patricia::Node* Patricia::Search(const std::string& findKey) const{
    Node *currentNode = root->left, *prevNode = root;

    while(currentNode->index > prevNode->index){
        // Index of char that we need to check
        size_t charIndex = (currentNode->index - 1) / BIT_COUNT;

Первым делом мы должны получить индекс символа, который нам надо проверять из исходной строки. Берем индекс из текущего узла, вычитая 1. Дальше делим на константу BIT_COUNT. Вычитаем 1 потому, что у нас индексы начинаются не с 0, а с 1. Допустим возьмем из патриции 1 вершину "m", у нее индекс 5 - 1 = 4, при делении на BIT_COUNT мы получим 0, поэтому проверяем из исходной строки нулевой символ, если бы мы не вычитали, то получили бы индекс 1, что неправильно.

Дальше стоит проверить, что индекс не выходит за размеры исходной строки:

    // FindKey is less than need char
    if(charIndex >= findKey.size()){
      // Remember prevNode
      prevNode = currentNode;
      // Only '0'
      currentNode = currentNode->left;
      continue;
    }

Если индекс выходит за размеры, то мы "как бы" берем бит из нулевого символа, битовая цепочка которого равна - 00000, то есть мы в любом случае получим бит 0, а это означает, что всегда будем переходить по левому указателю, запоминая текущую вершину в prevNode.

				char currentChar = findKey[charIndex];
        // How many times should we shift to the right
        int offset = (BIT_COUNT - 1 - ((currentNode->index - 1) % BIT_COUNT));
        // Get current bit
        bool currentBit = (currentChar >> offset) & 1;

        // Remember prevNode
        prevNode = currentNode;
        // If '1' go right, '0' go left
        currentBit  ? currentNode = currentNode->right
                    : currentNode = currentNode->left;
    }
    return currentNode;

Если индекс все таки не выходит за пределы размера искомого ключа, то мы должны взять текущий символ из строки. Высчитать смещение, т.е. насколько надо сместить битовую цепочку, чтоб нужный нам бит остался в самом крайнем правом положении, допустим нам надо взять первый бит из цепочки 10001, тогда смещение будет равно 4.

Получаем бит, применяя побитовую операцию И и сдвига, проще говоря если в конце битовой цепочки '1', то currentBit = true, если '0', то false.

Запоминаем текущую вершину, потому что сейчас будем передвигать ее. С помощью тернарного оператора делаем перемещение текущей вершины. Из метода Search возвращаем currentNode, когда индекс будет <= индексу предыдущей вершины. Полная функция выглядит так:

Patricia::Node* Patricia::Search(const std::string& findKey) const{
    Node *currentNode = root->left, *prevNode = root;

    while(currentNode->index > prevNode->index){
        // Index of char that we need to check
        size_t charIndex = (currentNode->index - 1) / BIT_COUNT;

        // findKey is less than need char
        if(charIndex >= findKey.size()){
          	// Remember prevNode
            prevNode = currentNode;
            // Only '0'
            currentNode = currentNode->left;
            continue;
        }

        char currentChar = findKey[charIndex];
        // How many times should we shift to the right
        int offset = (BIT_COUNT - 1 - ((currentNode->index - 1) % BIT_COUNT));
        // Get current bit
        bool currentBit = (currentChar >> offset) & 1;

        // Remember prevNode
        prevNode = currentNode;
        // If '1' go right, '0' go left
        currentBit  ? currentNode = currentNode->right
                    : currentNode = currentNode->left;
    }
    return currentNode;
}

Стоит заметить, что я не проверяю наличие корня, все из-за того, что данный метод в приватном доступе, и каждая функция перед вызовом Search проверяет наличие корня. Если вы делаете другую реализацию, то моя реализация может сломать вашу программу :с

Добавление пары в дерево

Алгоритм добавления пары в дерево:

1. Найти вершину, если она существует, то выдать ошибку, если нет, то (2).

2. Найти битовую разницу между ключами найденной вершины и добавляемой.

3. Пройтись снова от корня, найти вершину с индексом больше добавляемой.

4. Вставить новый узел между найденной вершиной и его родителем.

5. Связать указатели, один из них направлен на добавляемую вершину, другой на найденную(из п. 3).

void Patricia::Add(const std::string& key, int value){
    if(!root){
        root = new Node(key, value, 0);
        root->left = root;
        return;
    }

    Node *foundNode = Search(key);
    if(foundNode->key == key)
        throw std::runtime_error("\t\"" + key + "\" already exist!\n");

В данном методе я уже проверяю наличие корня, если он не существует, то создаю и соединяю, иначе нахожу вершину и сравниваю ключ найденной вершины с добавляемой, если равны, то выдаю ошибку.

		bool run = true;
    size_t charIndex = 0;
    while(run){
        char foundedKey = (foundNode->key.size() > charIndex 
                           							? foundNode->key[charIndex] : '\0');
        char inputKey   = (key.size() > charIndex ? key[charIndex] : '\0');
        for(size_t i = 0; i < BIT_COUNT; ++i){
            bool foundedKeyBit = foundedKey >> (BIT_COUNT - 1 - i) & 1;
            bool inputKeyBit = inputKey >> (BIT_COUNT - 1 - i) & 1;
            if(foundedKeyBit != inputKeyBit){
                Insert(key, value, charIndex * BIT_COUNT + i + 1);
                run = false;
                break;
            }
        }
        ++charIndex;
    }

Run является флагом для работы цикла while, charIndex - индекс символов, который надо брать из ключей, нужен, чтобы проверить все символы из ключей. foundedKey - берет текущий символ из ключа узла, с помощью тернарного оператора проверяем выходим ли за пределы ключа, если нет, то берем по индексу, иначе просто нулевой символ '\0'. Аналогично с inputKey - который берет символ из входящего ключа.

В цикле for проходим по битам, взятых символов, и пытаемся найти различающиеся. bool foundedKeyBit - сдвигает и выполняет операцию побитового И с найденным ключом. Аналогично с inputKeyBit.

Проверяем разницу между битами, если она есть, то вызываем функцию Insert, останавливаем два цикла. Заканчиваем на этом метод Add.

Вставка узла в дерево

Функция вставки не особо сильно отличается от поиска, добавлен один параметр, который указывает об индексе несовпадающих битов и одно условие, часть метода:

void Patricia::Insert(const std::string& key, const int& value,
                      																		const size_t& index){
    Node *currentNode = root->left, *prevNode = root;

    while(currentNode->index > prevNode->index && currentNode->index <= index){
        size_t charIndex = (currentNode->index - 1) / BIT_COUNT;
        // FindKey is less than need char
        if(charIndex >= key.size()){
            prevNode = currentNode;
            // Only '0'
            currentNode = currentNode->left;
            continue;
        }
        char currentChar = key[charIndex]; // If findkey.size less than currentNode->index
        int offset = (BIT_COUNT - 1 - ((currentNode->index - 1) % BIT_COUNT));
        bool currentBit = (currentChar >> offset) & 1;

        // Remember prevNode
        prevNode = currentNode;
        // If '1' go right, '0' go left
        currentBit  ? currentNode = currentNode->right
                    : currentNode = currentNode->left;
    }

В итоге, получим, что currentNode - вершина, индекс которой выше индекса вставляемого узла, а prevNode - вершина, индекс которой ниже индекса вставляемого узла. Теперь надо связать их:

		char getCharFromKey = key[(index - 1) / BIT_COUNT];
    bool getBit= getCharFromKey >> (BIT_COUNT - 1 - (index - 1) % BIT_COUNT) & 1;
    Node *newNode = new Node(key, value, index);

    if(prevNode->left == currentNode)
        prevNode->left = newNode;
    else
        prevNode->right = newNode;

    getBit  ? (newNode->right = newNode, newNode->left = currentNode)
            : (newNode->left = newNode, newNode->right = currentNode);
}

Так как у нас в параметрах уже есть все 3 значения, которые нам нужны, то getCharFromKey равен символу исходного ключа по индексу (index - 1) / BIT_COUNT. Также получаем и бит из символа. Создаем новый узел с тремя параметрами.

prevNode - это вершина-родитель нашего нового узла, поэтому надо его связать с ребенком нового узла. Проверяем, что prevNode->left == currentNode, если true, то от родителя уходим влево и попадаем в новый узел, связываем левый указатель родителя с новым узлом.

Дальше надо установить указатели нового узла. Проверяем, что бит, который мы получили из getBit, который в свою очередь получает бит из нового ключа, используя индекс, который высчитали в функции Add, равен true, то тогда правый указатель нового узла направлен на самого себя, а левый на текущий, то есть вершину-ребенка. Иначе наоборот. Приведу визуализацию:

Мы хотим добавить в патрицию_1 новый узел с ключом "n" - 01110.

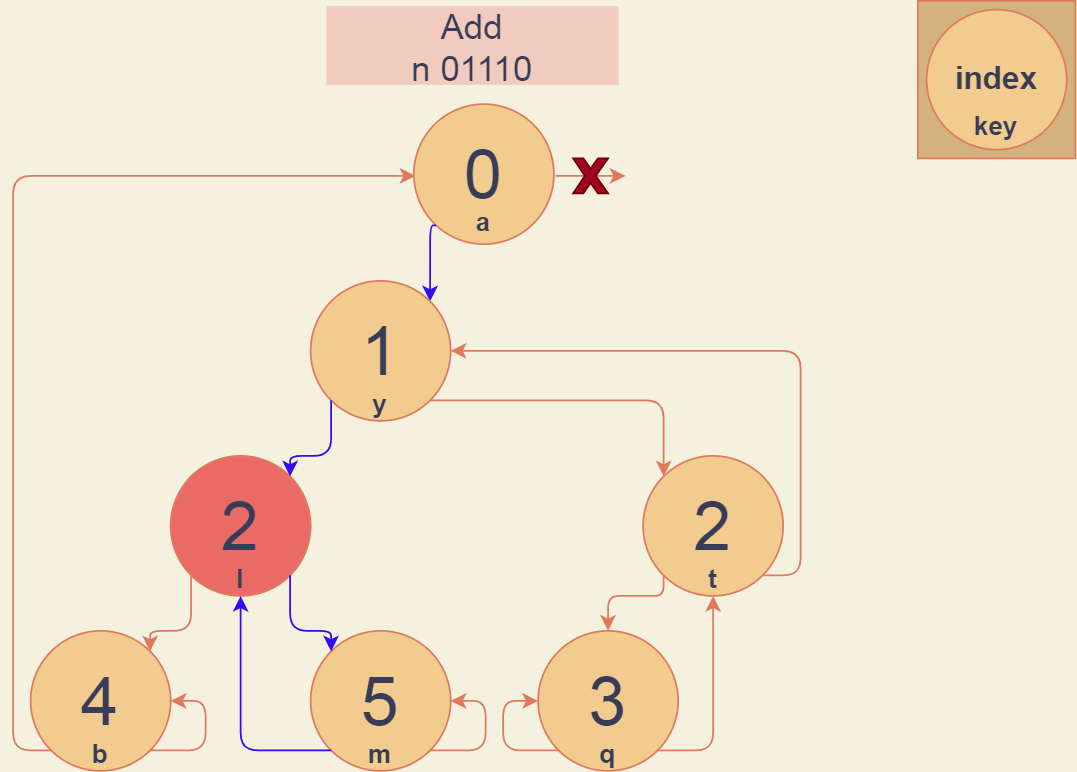
Поиск выдал нам результат - вершину "l" с индексом 2. Ищем различия в найденном и исходном битах. l - 01100, n - 01110, различие в 4 бите. Запускаем функцию Insert.

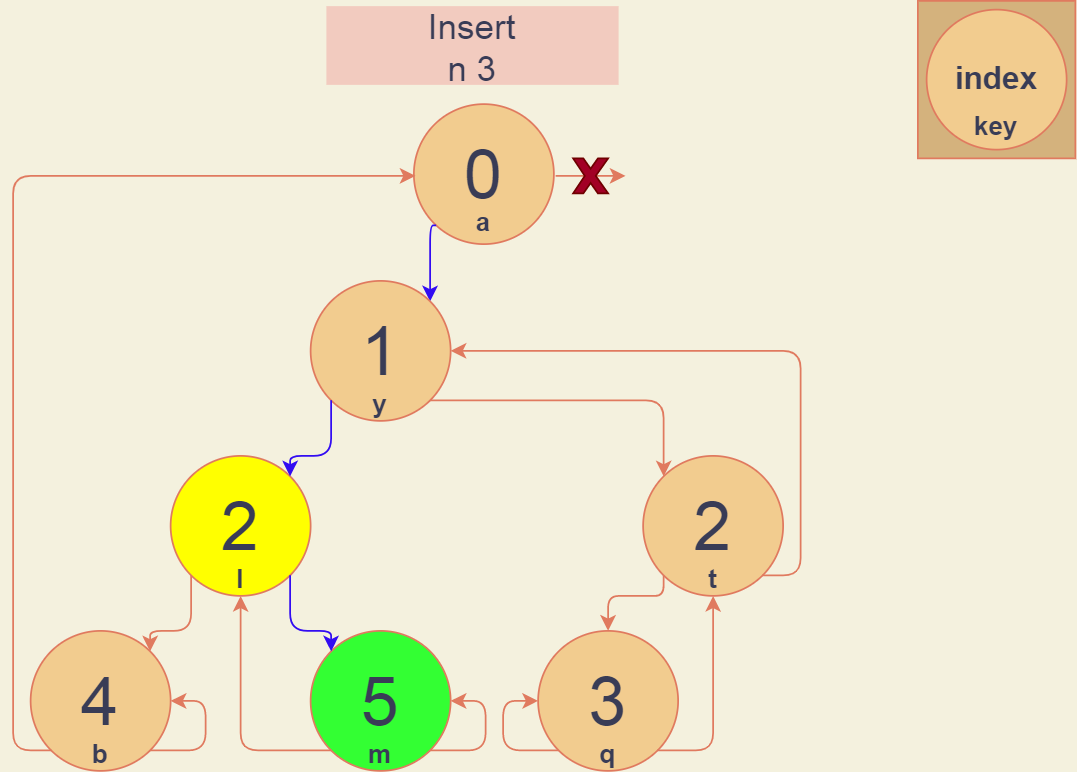
Функция Insert находит две связанные вершины, между которыми надо вставить новую. Зеленая вершина имеет индекс выше исходного(4), а желтая - ниже.

Фух... Теперь немножко отдохнем, буквально на 5 секунд, реализуем функцию получения значения из дерева.

Функция At

int& Patricia::At(const std::string& findKey) const{
    if(!root)
        throw std::runtime_error("\t\"" + findKey + "\" hadn't found!\n");

    Node* get = Search(findKey);

    if(get->key == findKey)
        return get->value;

    throw std::runtime_error("\t\"" + findKey + "\" hadn't found!\n");
}

Я думаю добавлять нечего, мы сначала проверяем корень, дальше используем функцию поиска, проверяем найденный узел, в случае правильности - возвращаем значение, иначе ошибку.

Возвращаю по ссылке, так как я уверен в том, что возвращенное значение будет существовать, а не удалится.

Ну, отдохнули, теперь самое сложное - удаление. Здесь существует 4 варианта удаления узла:

1. Если удаляемый узел - корень и он один элемент в дереве, тогда просто удаляем корень и делаем указатель nullptr.

2. Если удаляемый узел - лист, тогда просто связываем родителя с оставшимся потомком и удаляем вершину.

3. Если владелец удаляемого элемента - лист, тогда просто связываем родителя владельца с удаляемым элементом.

4. В остальных случаях нам надо найти 3 вершины, А - удаляемый узел, Б - владелец удаляемого узла, В - владелец владельца удаляемого узла.

В приведенном примере выше удаляем вершину "t", ее же будем называть вершина А, ее владелец вершина "z", она же вершина Б, ее владелец вершина "y", она же вершина В. Теперь алгоритм удаления узла А:

1. Копируем ключ и значение узла Б в узел А.

2. Связываем родителя узла Б с ребенком узла Б.

3. Перенаправляем указатель вершины В с Б на А.

4. Удаляем вершину Б.

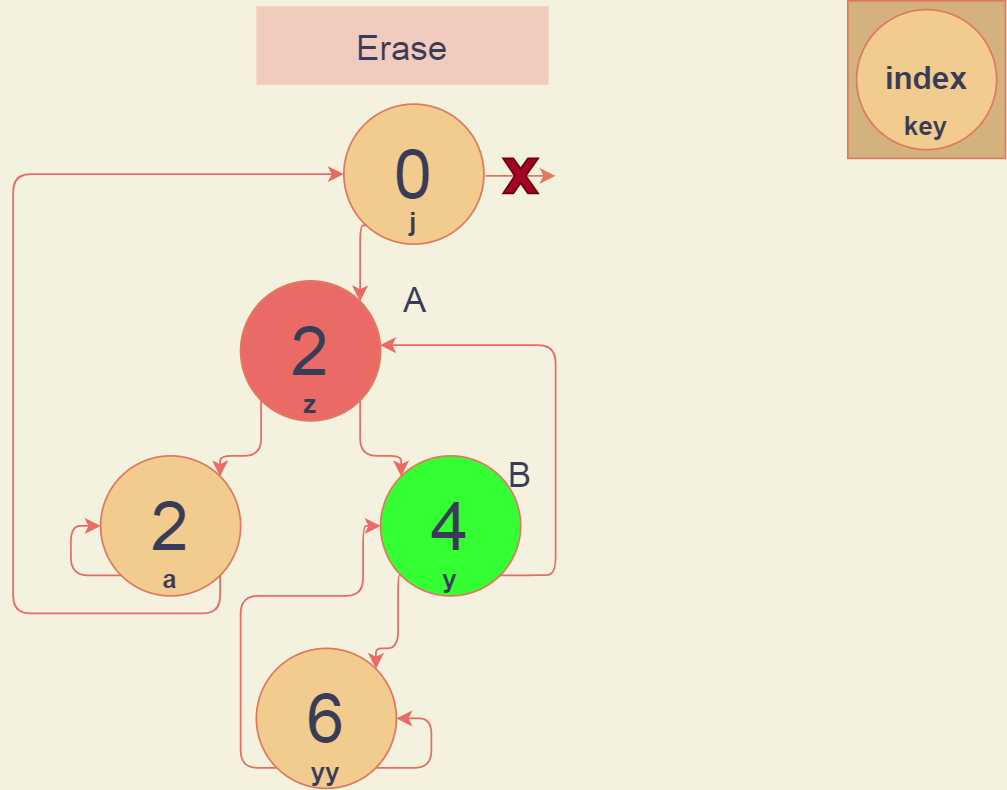
В результате получаем такое дерево. Но у нас есть проблема, теперь нам надо использовать родителя, а это означает, что надо либо иметь указатель в самой структуре вершины на родителя, либо как-то возвращать из функции больше одного указателя. Так как я делал оптимизированную патрицию, то я решил не делать указатель на родителя, ведь тогда нам потребуется очень много памяти, я использовал возвращение из функции 3 указателей через кортежи, функция поиска никак особо не поменялась:

std::tuple<Patricia::Node*, Patricia::Node*, Patricia::Node*>
                      Patricia::SearchE(const std::string& findKey) const{
    Node *currentNode = root->left, *prevNode = root, *prevPrevNode = root;
    while(currentNode->index > prevNode->index){
        size_t charIndex = (currentNode->index - 1) / BIT_COUNT;

    // FindKey is less than need char
    if(charIndex &gt;= findKey.size()){
        prevPrevNode = prevNode;
        prevNode = currentNode;
        // Only '0'
        currentNode = currentNode-&gt;left;
        continue;
    }

    char currentChar = findKey[charIndex];// If findkey.size less than currentNode-&gt;index
    int offset = (BIT_COUNT - 1 - ((currentNode-&gt;index - 1) % BIT_COUNT));
    bool currentBit = (currentChar &gt;&gt; offset) &amp; 1;

    // Remember prevNode &amp; prevPrevNove
    prevPrevNode = prevNode;
    prevNode = currentNode;
    // If '1' go right, '0' go left
    currentBit  ? currentNode = currentNode-&gt;right
                : currentNode = currentNode-&gt;left;
}

return std::make_tuple(currentNode, prevNode, prevPrevNode);

}

Давайте медленно смотреть метод удаления, чтоб не сломать психику с:

void Patricia::Erase(const std::string& key){
    if(!root)
        throw std::runtime_error("\t\"" + key + "\" hadn't found!\n");

    // Get delete node, owner delete node and parent owner
    std::tuple<Node*, Node*, Node*> delOwnerParentTuple = SearchE(key);
    // A
    Node *deleteNode = std::get<0>(delOwnerParentTuple);
    // Б
    Node *ownerDeleteNode = std::get<1>(delOwnerParentTuple);
    // Б parent
    Node *parentOwnerDeleteNode = std::get<2>(delOwnerParentTuple);

    if(deleteNode->key != key)
        throw std::runtime_error("\t\"" + key + "\" hadn't found!\n");
    
    // If delete node is root and it's one
    if(deleteNode == root && root->left == root){
        delete root;
        root = nullptr;
        return;
    }

Пока что мы просто ищем нужный удаляемый элемент и возвращаем кортеж и удаляемого элемента, его владельца и родителя владельца, их же разыменовываем в указатели. Дальше проверяем, что мы нашли нужный ключ. Дальше проверяет 1 вариант удаление, когда корень один в дереве, его нужно удалить.

    // If delete node is leaf
    if(ownerDeleteNode == deleteNode){
        if(parentOwnerDeleteNode->right == deleteNode)
            if(deleteNode->right == deleteNode)
                parentOwnerDeleteNode->right = deleteNode->left;
            else
                parentOwnerDeleteNode->right = deleteNode->right;
        else
            if(deleteNode->right == deleteNode)
                parentOwnerDeleteNode->left = deleteNode->left;
            else
                parentOwnerDeleteNode->left = deleteNode->right;
        delete deleteNode;
        return;
    }

    // Get owner owner delete node
    std::tuple<Node*, Node*, Node*> ownerOwnerTuple = 
                                               SearchE(ownerDeleteNode->key);
    Node *ownerOwnerDelNode = std::get<1>(ownerOwnerTuple);

    // Change item from owner delete node to delete node
    deleteNode->key = ownerDeleteNode->key;
    deleteNode->value = ownerDeleteNode->value;

Если удаляемый узел - лист, то связываем родителя и предка. Иначе опять ищем, но уже узел Б, нам нужен его владелец, в кортеже использует только лишь 2 указатель, поэтому при разыменовании, используем только std::get<1> в строке 20. Меняем ключ и значение узла А на ключ и значение узла Б.

    // If owner delete node is leaf
    if(ownerOwnerDelNode == ownerDeleteNode){
        if(parentOwnerDeleteNode->right == ownerDeleteNode)
            parentOwnerDeleteNode->right = deleteNode;
        else
            parentOwnerDeleteNode->left = deleteNode;
    }
    else{
        // Tie parent owner delete node with child
        if(parentOwnerDeleteNode->right == ownerDeleteNode)
            if(ownerDeleteNode->right == deleteNode)
                parentOwnerDeleteNode->right = ownerDeleteNode->left;
            else
                parentOwnerDeleteNode->right = ownerDeleteNode->right;
        else
            if(ownerDeleteNode->right == deleteNode)
                parentOwnerDeleteNode->left = ownerDeleteNode->left;
            else
                parentOwnerDeleteNode->left = ownerDeleteNode->right;

        if(ownerOwnerDelNode->right == ownerDeleteNode)
            ownerOwnerDelNode->right = deleteNode;
        else
            ownerOwnerDelNode->left = deleteNode;
    }
    delete ownerDeleteNode;
}

Если узел Б - лист, то тогда связываем родителя с удаляемым узлом. Иначе связываем родителя и ребенка узла Б, а вершину В направляем к узлу А, в конце двух случаев удаляем вершину Б.

Осталось самое простое - удалить все вершины, когда нам надо будет выходить из программы, чтоб не было утечек памяти.

Функция Clear

Одна функция у меня в публичном доступе, другая в приватном, я реализовал все на основе рекурсии:

void Patricia::Clear(){
    if(!root)
        return;
    if(root != root->left)
        ClearNode(root->left);
    delete root;
    root = nullptr;
}

Публичная функция, которая проверяет корень, что он не один в дереве, если не один, то вызывает приватный метод очищения конкретного узла:

void Patricia::ClearNode(Node *node){
    if(node->left->index > node->index)
        ClearNode(node->left);
    if(node->right->index > node->index)
        ClearNode(node->right);

    delete node;
}

Приватная функция удаления узла, просто вызывает такое же удаление для детей текущего узла, а потом удаляет саму вершину.

Финальный интерфейс

Браво, ты дошел до этого момента и почти не выстрелил себе в ногу, давай порадуемся, посмотрим на интерфейс нашей патриции:

// patr.hpp
#pragma once
#include <string>
#include <tuple>

// Bits u need in one char
const int BIT_COUNT = 5;

typedef class Patricia{
private:
    struct Node;
    Node *root = nullptr;
    // Search but return 3 nodes
    std::tuple<Node*, Node*, Node*> SearchE(const std::string& findKey) const;
    // Search return only 1 node
    Node* Search(const std::string& findKey) const;
    // Insert node to tree
    void Insert(const std::string& key, const int& value, const size_t& index);
    void ClearNode(Node *node);
public:
    // Get value from map
    int& At(const std::string& findKey) const;
    // Create node with key value and insert to tree
    void Add(const std::string& key, int value);
    // Delete node from tree
    void Erase(const std::string& key);
    void Clear();
    ~Patricia(){ Clear(); }
} patr;

Совмещаем с пользователем

#include "patr.hpp"
#include <iostream>
#include <time.h>

int main(){
    patr test;
    std::string command;
    time_t start = clock();
    while(std::cin >> command && command != "\x4"){
        if(command == "+"){
            std::string key; std::cin >> key;
            int value; std::cin >> value;
            try{
                test.Add(key, value);
                std::cout << "\tSuccessfully!\n";
            }
            catch(const std::runtime_error& e){
                std::cout << e.what();
            }
        }
        else if(command == "-"){
            std::string key; std::cin >> key;
            try{
                test.Erase(key);
                std::cout << "\tSuccessfully!\n";
            }
            catch(const std::runtime_error& e){
                std::cout << e.what();
            }
        }
        else if(command == "clear" || command == "new"){
            test.Clear();
        }
        else if(command == "get"){
            try{
                std::string key; std::cin >> key;
                std::cout << test.At(key) << '\n';
            }
            catch(const std::runtime_error& e){
                std::cout << e.what();
            }
        }
        else if(command != "\n"){
            std::cout << "\tCommand \"" + command + "\" isn't available\n";
        }
    }
    std::cout << "Time: " << (double)(clock() - start)/CLOCKS_PER_SEC << '\n';
    return 0;
}

Вводим команды(можете ввести свои) до тех пор, пока не введем Ctrl+D. Команды:

• + (key) (value) - добавляет узел в дерево

• - (key) - удаляет узел из дерева

• get (key) - получает int, если существует такой ключ

• clear - очищает полностью дерево

Вывожу время работы патриции, чтоб можно было сравнить ее работу выполнения.

Кстати, сложность работы всех методов O(h), где h - высота дерева.

Заключение

Если вы дошли сюда вместе со мной, то вы молодцы, а я кажется стал понимать почему так мало информации про патрицию, она достаточно сложная, особенно в обучении и собственной реализации. Но я смог создать свою патрицию с сильной экономией памяти, пытался сделать код максимально читабельным. Ну и конечно скидываю исходники, чтоб вам было проще по ним смотреть и читать.

GitHub