
Есть ли у вас необходимый запас знаний для изучения философии в Оксфорде? Предлагаем вашему вниманию загадки на эпистемическую логику – то есть, связанные с рассуждениями о самом знании. Но я знаю, что вы знаете, что я знаю, что вы это знаете.
Все три задачки в последние годы задавались во время собеседований при поступлении в Оксфордский университет на философский факультет. В каждой из задач есть первоначальный вопрос, и почти все кандидаты правильно ответили на него. Далее в тексте идут дополнительные вопросы, с которыми справились только лучшие из лучших.
Задачи
1. Сюрприз Стефани
Стефани пригласила к себе домой своих друзей, Рому и Свету. Все они обладают безупречной логикой. Она сказала им, что под одним из синих квадратов находится сюрприз.

Роме она сообщила номер ряда, в котором находится сюрприз, а Свете – номер столбца, и каждый из них знает об этом. Происходит следующий диалог:
Рома: не знаю, где находится сюрприз, но я знаю, что и Света этого не знает.
Света: да, я сначала действительно не знала, где он находится. Но теперь знаю.
Рома: ну в таком случае я теперь тоже знаю.
Вопрос: где находится сюрприз?
Дополнительные вопросы. Допустим, до этого разговора кто-то из гостей споткнулся о клеточку B1, и оказалось, что она пустая. А) Будет ли иметь смысл описанный разговор? Б) Удивился ли кто-то из гостей, что клетка В1 пустая? В) Как изменился бы диалог, если бы оба гостя знали, что клетка В1 пустая? Г) Почему из-за информации о том, что В1 пустая, утверждение Ромы становится ложным? (это самый интересный момент в загадке, поскольку кажется парадоксальным, что добавление информации может уменьшить знание).
2. Вечеринка с плитками
На вечеринке с очень логичными философами Светой и Колей сюрприз был спрятан под одной из этих цветных плиток.

Каждому из них сообщили информацию о местонахождении сюрприза:
— Света знает форму плитки;
— Коля знает цвет плитки.
Все знают, что им сообщили только это, и больше ничего.
Хозяин вечеринки: Кто-нибудь знает, где сюрприз?
Неловкое молчание.
Хозяин вечеринки: А теперь кто-нибудь знает?
Неловкое молчание.
Света и Коля, одновременно: Теперь я знаю, где сюрприз!
Вопрос: где сюрприз?
Дополнительные вопросы. А) Ожидал ли кто-то из гостей первого неловкого молчания? Б) Каким образом оно на них повлияло? Что они узнали из него? В) Знал ли Коля, что Света знает, что Коля не знал изначально, где находится сюрприз? Г) Ожидал ли кто-то из них второго молчания?
3. Коробки Алисы
Алиса пригласила своих друзей Кэролайн и Сьюзан к себе домой, и поставила перед ними на столе несколько коробок. Известно, что все гости обладают безупречной логикой.
На столе стоят:
— маленькая красная коробка;
— средняя красная коробка;
— большая чёрная коробка;
— маленькая синяя коробка;
— большая синяя коробка.
Алиса говорит друзьям, что в одной из коробок находится подарок, и что она сказала Кэролайн цвет коробки, а Сюзан – размер. Происходит следующий разговор:
Кэролайн: Я не знаю, в какой коробке подарок, и знаю, что Сюзан этого не знает.
Сюзан: Я ещё до твоей реплики знала, что ты не знаешь, в какой коробке подарок.
Кэролайн: А, ну теперь-то я поняла, в какой он коробке.
Вопрос: в какой коробке подарок?
Дополнительные вопросы. Знает ли теперь Сюзан, в какой коробке подарок? Если да, то кто из них догадался первым – Кэролайн или Сюзан?
Все задачки происходят из письменного стола математического философа Джоэла Дэвида Хэмкинса. Хэмкинс – профессор логики из Университетского колледжа в Оксфорде. Он говорит, что преподавателям в колледже нравится задавать абитуриентам задачи на логическое рассуждение, поскольку это показывает, как ученик подступается к размышлениям над новыми темами. «Также нам раскрывается личность поступающего, наличие у него настойчивости, способность рационально рассуждать о проблеме, о которой известно не всё, способность принимать от других полезные советы. Поэтому на собеседовании мы не только смотрим, может ли поступающий решить задачку сам по себе, но и наблюдаем за процессом его рассуждений. Всё это – ценные сведения для оценки его способностей».
На всякий случай, имейте в виду – в следующем году задачки будут уже другими!
Ответы
1. Сюрприз Стефани
Если Рома не знает, где находится сюрприз, значит, мы можем вычеркнуть 3-й ряд (поскольку если бы ему сказали, что сюрприз в третьем ряду, он бы сразу вычислил нужный квадрат). Если он знает, что Света не знает, где сюрприз, мы можем исключить 4-й ряд (поскольку Света знала бы, где сюрприз, только если бы он был в квадрате С4). Если Света догадалась, где лежит сюрприз, то ей должен быть известен единственный столбец, для которого остался только один вариант. Это столбец А – следовательно, сюрприз находится в квадрате А2.
Дополнительные вопросы. А) Нет. Теперь вторая часть первого утверждения Ромы неверна. Б) Нет. Они оба знали, что в В1 сюрприза нет. В) Они узнавали о знаниях друг друга. Г) Рома знал, что Света чего-то не знает. Добавление информации привело к потере им этого знания, потому что тогда он не знал бы, что она чего-то не знает. Дополнительная информация могла бы дать ей новые знания. Если бы сюрприз находился в квадрате В2, она бы узнала об этом, узнав, что в В1 ничего нет.
2. Вечеринка с плитками
Света могла бы знать, где находится сюрприз, ещё до этого диалога, только если бы ей сказали, что сюрприз находится под квадратной плиткой. Коля знал бы, если бы ему назвали жёлтый цвет. Поскольку они этого не знает, мы можем вычеркнуть квадрат и жёлтую плитку. Если бы Свете сказали «круг», она бы теперь знала правильную плитку – поскольку у нас осталась только одна плитка. Если бы Коле сказали «синий», он бы тоже понял, где сюрприз. Но поскольку они оба промолчали и после второго вопроса, можно предположить, что правильную плитку они не знают. Из этого следует, что цвет должен быть красный, а форма – треугольная.
А) Да. Света изначально знает, что Коля не знает местоположения сюрприза, поскольку у обоих треугольников есть парные фигуры того же цвета. Коля тоже знает, что Света не знает, где сюрприз, поскольку она знает, что цвет – красный, и у обоих красных плиток есть пары той же формы. Б) Они узнали, что другой человек теперь знает, что им неизвестно местоположение приза. В) Нет. Хотя он знал, что цвет красный, это могла быть круглая плитка, а в таком случае Света не знала бы, что Коля не знает, где сюрприз – она могла решить, что он может быть под жёлтым кругом. Г) Нет, никто из них его не ожидал. С точки зрения Коли сюрприз мог оказаться под красным кругом, а тогда Света ответила бы после первого молчания – но этого не произошло. С точки зрения Светы сюрприз мог оказаться под синим треугольником, а тогда Коля ответил бы после первого молчания, но этого не произошло.
3. Коробки Алисы
Загадка кажется более сложной из-за отсутствия рисунка. Облегчить задачу можно, нарисовав сетку 3х3, в которой красный, чёрный и синий цвета соответствуют столбцам, а маленький, средний и большой – строкам. Возможные варианты коробок:
- XOX
- XOO
- OXX
Если Кэролайн неизвестна коробка, ей не сказали «чёрный». Если она знает, что Сюзан неизвестна коробка, ей не сказали «красный» – иначе был бы шанс, что Сюзан сказали «средний», а в таком случае Кэролайн не могла бы сказать, что она точно знает, что Сюзан неизвестно, в какой коробке сюрприз. Из этого следует, что Кэролайн сказали «синий».
Если бы до того, как Кэролайн произнесла свою фразу, Сюзан знала, что Кэролайн не известна правильная коробка, мы могли бы исключить возможность того, что Сюзан сказали «большая». Поскольку в таком случае она не знала бы точно, что Кэролайн не знает, в какой коробке сюрприз – она не могла бы исключить возможность, что приз находится в большой чёрной коробке, ведь тогда Кэролайн знала бы, где сюрприз. Поскольку коробка синяя и не крупная, остаётся только один вариант – маленькая синяя коробка.
Сюзан первая узнала, в какой коробке сюрприз. Она узнала это, как только Кэролайн произнесла первое предложение, поскольку после этого Сюзан знает, что коробка синяя. А поскольку она знает, что коробка маленькая, вариант только один – маленькая синяя коробка.
Комментарии (93)

thecove
20.10.2021 05:11+7Мда.... в Оксфорд я бы не поступил.

JPEGEC
20.10.2021 05:37+7Вероятно в Оксфорде можно заняться изучением чего-то еще кроме философии?

Admaer
20.10.2021 09:12+2Подозреваю, что зис из вери квалити транслатион и наследие средневековой системы высшего образования, когда во многих европейских и американских ВУЗах есть всего четыре докторских степени: доктор медицины (врачи), доктор теологии (не знаю, священники?), доктор юриспруденции (юристы) и доктор философии (вообще все остальные области знания). Поэтому это вопросы, видимо, для всех тех, кто поступает не на врача, юриста или жреца.

tyomitch
20.10.2021 09:30+2Несмотря на то, что степень PhD получают не только философы, эти вопросы -- конкретно для философов; и не для аспирантов, претендующих на PhD, а для бакалавров, в чьём названии степени (BA) вообще нет слова "философия".

max_mustermann
21.10.2021 23:21Эти вопросы подходят для всех дисциплин где важна формальная логика.
>для бакалавров, в чьём названии степени (BA) вообще нет слова "философия"
Это просто традиция, еще 100 лет назад они прямо так и назывались "Bachelor of Philosophy", как промежуточный титул перед специализацией.

max_mustermann
21.10.2021 23:15-1Да, философия в данном случае - это "натуральная философия", т.е. естественные науки.
Еще из "классических" факультетов есть Art, к которому относятся всякие "гуманитарные" науки, у меня знакомый закончил какой-то классический британский универ типа Оксфорда по бизнесс-менеджмент и стал гордый "Bachelor of Arts"

tyomitch
22.10.2021 11:33Да, философия в данном случае - это "натуральная философия", т.е. естественные науки.
На основании чего вы сделали такой вывод?

Akon32
20.10.2021 07:02+7Задачи напоминают iq-тест.

IgorPie
20.10.2021 11:09+1Задачку Эйнштейна, вроде вот этой

Alexandroppolus
20.10.2021 11:24Никогда не понимал, почему там кусок условия называют "подсказками"

Siddthartha
20.10.2021 23:09потому что каджое из них эквивалентно биту в квадрате, подобному тому, что в оксфордской головоломке из статьи (если записать предикатами и свести к КНФ или ДНФ)
и это помогает. есть даже вариант с фруктами в клетках квадрата.. каждый фрукт -- переменная системы линейных уравнений) можно так
ЗЫ: в науке и жизни фрукты те были, вроде)

631052
20.10.2021 12:21там весь интерес, чтоб в уме.
честно скажу, не смог. с бумажками-то да, а вот запомнить всех этих

Vilaine
20.10.2021 21:48+1Для её решения нужно намного больше оперативной памяти, чем для тех, что в статье. Я могу её решить только со многих попыток (постоянно забываю предыдущие логические вычисления), а те, что в статье, не требуют этого. Просто поперебирать несколько ветвей пару раз. Если решать на бумаге, то никакой IQ не нужен, достаточно быть прологом, наверно.

Siddthartha
20.10.2021 23:05да, простенький вариант этого квадрата эйнштейна, на быструю проверку принципа системы уравнений) я пока только первую задачу попробовал, но довлен. зная принцип -- около минуты-двух. быстро осенило, что две/две должно быть кнопки в изместных им _кортежах_)
. а вот на тот, полный, вариант и впервые, я помню, очень прилично времени потратил.

mark_ablov
20.10.2021 07:36+20То ли я навострился на таких задачах в школе/универе, то ли они действительно несложные, но каждая решается за минуту. Дополнительные вопросы поинтереснее, но тоже не rocket science.

SnakeSolid
20.10.2021 07:42+6Если понимать принцип решения, то да — они не сложные. Если не понимать, то можно долго даже над первой сидеть, где все на сетке показано.

631052
20.10.2021 12:05+8-- не правда ли всё просто, Ватсон.
-- действительно, очень просто. после того, как ВЫ мне объяснили.. ((
(с)

DreamShaded
20.10.2021 12:07+4угу. Когда-то на брейнгеймс решал такие)) там серия задач на логику с Мегамозгом. До сих пор помню ещё задачу про встречу Мегамозгов, где один говорит тоже неполную информацию о возрасте детей, а второй с двух вопросов угадывает) https://braingames.ru/?path=comments&puzzle=98
А вчера в офисе залипли на такую задачку, всё никак не верили, что ответ может быть настолько большим:
надо найти целые положительные a, b, c

AllexIn
20.10.2021 08:45+2Достаточно простые задачи. По сути просто обычные уравнения.
Если отбросить все эти кубики треугольнички и работать с переменными - получается математика средней школы.

leok
20.10.2021 09:03+4А как неловкое молчание описывается переменными?

AllexIn
20.10.2021 09:06+4Это однозначно трактуется как "нет знающих". Что добавляет информации.
Я об этом и говорю: нужно отбросить всю мишуру(пример которой вы и привели) и оставить чистую информацию.

JPEGEC
21.10.2021 08:25+1Можете показать систему уравнений для первой задачи, к примеру?
У меня вот сходу составить не вышло.

unsignedchar
21.10.2021 09:54Там будут уравнения из дискретки. В нашей школе такого точно не учили ;)

Alexandroppolus
20.10.2021 09:56+5Вступительный экзамен в ШАД определенно посложнее будет

pehat
21.10.2021 02:06+4Зато туда не надо сдавать английский. Как известно, советский учёный, знающий английский - это уже американский учёный.

Intuist
20.10.2021 12:04Отлично. Сначала засомневался из-за предположения, что может быть неправильный перевод, а потом вник и всё реально по тексту и очень логично! Просто шикарные загадки.

ZhuchekOleg
20.10.2021 12:05+2Ничего сложно. Задачи быстро решаются. Логика присутствует. Простенький экзамен короче...

moooV
20.10.2021 12:59+7Даже после прочтения ответов я не понял. Походу, я тупой. А ведь в R&D работаю — но там надо специфику своей предметной области глубоко знать (компьютерная графика), не логику или олимпиадные задачки.
Жена (кстати, тоже айтишник) легко решила и говорит что я не могу потому что у меня женская логика. А у нее классическая формальная и в совместной жизни с ней спорить тяжело, я часто делаю ОЙ ВСЁ и ухожу из спора. ????♂️
Но и на IQ она меня много раз тестировала (тк думала что я тупой) — нет, все даже выше среднего. Но тут задачки вообще не похожие.
Может это потому что я эмоциональный экстраверт с кавказскими корнями, а она — типичный интроверт, лол.

gmixo
20.10.2021 15:14первую решил правильно,
рассуждения по 2й показались не логичными, и там все условно и имхо имеет несколько решений
3ю не стал читать =\
задачи прикольные

DoNotPanic
20.10.2021 18:48+1Задача 1:
Г) Почему из-за информации о том, что В1 пустая, утверждение Ромы становится ложным? (это самый интересный момент в загадке, поскольку кажется парадоксальным, что добавление информации может уменьшить знание).
Похоже, что да, в таком случае Рома и Света не смогут узнать, где находится приз, ведя диалог по той же логике.
Однако — возможен «финт ушами»:Рома: ЕСЛИ БЫ клетка B1 была синей, то ситуация была бы следующая...
И сводим разговор к предыдущему.
Хотя это угадать непросто, но формально информация не потерялась, её ещё можно добыть!

zhaparoff
20.10.2021 19:56+2Задачки на один зуб для тех кто хоть раз держал в руках сборник «Математические головоломки и развлечения» от Мартина Гарднера. Отличная штука для развития навыков счета, логики, пространственного мышления и способности нестандартно взглянуть на вещи.

vesper-bot
21.10.2021 07:16Кстати да, в этой книге задачи на "знаю-не знаю" как дополнительные источники информации были.

bilayan
20.10.2021 20:48+1Аналог первой задачки буквально полторы недели назад вспоминали тут в коментариях. Только там были султан и 2 числа и 2 мудреца: Али-ибн-Вали и Вали-ибн-Али.

azatSomeCode
20.10.2021 23:13+2Задачки не сложные. Тем более они все похожи. Они все легко решаются методом исключения.

akhkmed
20.10.2021 23:53+7Во второй задаче хозяин вечеринки в роли тактового генератора в конечном автомате.

chilicoder
21.10.2021 00:34Первая задача, прямо калька со знаменитой "задачи для сингапурских школьников"

charypopper
21.10.2021 15:33+1Задачи интересные, но важен контекст - сколько времени дается на размышления?

olegbask
21.10.2021 19:46-1Я один не понял формулировку первой задачи? Если сюрприз под синим квадратом, это значит что квадрат над ним синий или то что он просто в синем квадрате находится?
Как люди с философского факультета не смогли придумать однозначную формулировку?! Или это трудности перевода…

unsignedchar
21.10.2021 20:21+2Как люди с философского факультета не смогли придумать однозначную формулировку?!
Тестировщик ищет сюрприз под синим квадратом. Под квадратом, находящимся ниже синего квадрата. За пределами видимой части экрана…

Dark_Purple
21.10.2021 22:29-3Я только недавно перестал наклейку от банана на лоб приклеивать, а тут такое????




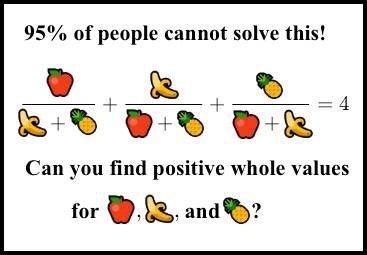

dron-KR
Первую задачку не смог решить и не понял как автор получил ответ адва?
Если кто объяснит, буду признателен
SLY_G Автор
Если бы Роме сказали, что сюрприз в 3-м ряду, он бы сразу понял, что ему нужен квадрат А3. Значит, это не третий ряд. Вычёркиваем.
Дальше он говорит, что точно знает, что Света не знает, где сюрприз. Это значит, что и 4-й ряд тоже вычёркиваем. Потому что во всех столбцах, кроме С, есть по нескольку клеток, где может быть сюрприз, а в столбце С - только одна. Поэтому если бы ему назвали 4-й ряд, то была бы вероятность, что сюрприз лежит в С4, и Свете сказали бы про столбец С. Но ему сказали про другой ряд, не про 4-й. А во всех остальных рядах, кроме 4-го, в столбце С нет ячеек, где может лежать сюрприз. Следовательно, Свете сказали про другой столбец, не С. Следовательно, Света никак не может узнать, где приз, потому что во всех остальных столбцах есть по несколько вариантов ячеек.
После этого Света говорит - а, ну теперь-то я знаю, где сюрприз. Как она могла это вычислить? Единственным способом. Если вычеркнуть с картинки ряды 3 и 4, а также столбец С, то единственный столбец, где будет только один вариант для сюрприза - это столбец А, потому что в столбцах В и D останется по два варианта.
Значит, сюрприз в ячейке А2.
Н-да, чем ещё заниматься в третьем часу ночи...
SShtole
Я на этом месте споткнулся. Откуда Рома знает, что Света не знает? Если всё, что знает Рома, это то, что Свете сообщили правильный столбец? Может это C и она сразу всё поняла.
Хороший тамада и конкурсы интересные )
swelf
Если это столбец C, то у ромы ряд 4. И тогда он не может однозначно сказать, что света не знает(а вдруг и правда С). А раз может одназначно сказать, то у него один из рядов 1-2
Physmatik
Рома точно знает, что Света не знает. Если бы ему сказали "4", то один из вариантов столбца был бы "С", и Света могла бы, в какой-то части случаев, знать местоположение подарка. Но так как ему сказали "2", то он видит, что ни один из вариантов {"A", "B", "D"} не даст Свете точного местоположения, то есть какой-бы столбец ей не сказали, она не сможет узнать место только по столбцу.
SShtole
А, понял. Ему же сказали: «2», значит C исключён. Мда, прощай, Оксофорд!
sergio_nsk
Зачем-то изменили классическую задачу, в котрой диалог был бы таким:
Света: Я не знаю, где он находится.
Рома: И я не знаю.
Света: Теперь я знаю.
Рома: Ну в таком случае я теперь тоже знаю.
Stronczzz
Спасибо! Действительно, самый ценный комментарий по первой задаче
edo1h
это другая задача
PocketM
А я не понял :(
Вычеркнули, теперь сюрприз может быть в 2A 2B 2D 1B 1D.
А как она перешла в состояние «не знаю» в «знаю»? Т.е. почему она решила, что сюрприз в столбце А?
Все понял, ей сообщили столбец А. Забыл, что ей тоже информацию сообщили…
NitrogenOne
Но если вычеркнуть ряды 1 и 3, а также столбец С, то снова будет только один вариант для сюрприза - столбец B. И тогда ответ будет зависеть от того, какой ряд вычеркнет Света, а таких рядов с единственным вариантом после вычёркивания целых 2.
shvez
Задачки шикарны. Первое впечатление - какого хрена?! как это можно решить?!
Я, кстати, тоже не решил первую. Выкинул столбец А. А потом застрял между B и D
Вообще задачи похожи. Скорее всего у них какой-то шаблон есть, на который они просто разные условия нанизывают и получают разные задачи
Спасибо, за интересный пост
MadMixture
"Это значит, что и 4-й ряд тоже вычёркиваем." - с этим не согласен, 4-й ряд тоже не давал Свете ответа. Возможно, ошибка картинки в том, что А4 должен быть белый!
Mes
Очень похоже на задачу про голубей:
---
Встречаются два приятеля - математика:
- Ну как дела, как живешь?
- Все хорошо, растут два сына дошкольника.
- Сколько им лет?
- Произведение их возрастов равно количеству голубей возле этой скамейки.
- Этой информации мне недостаточно.
- Старший похож на мать.
- Теперь я знаю ответ на твой вопрос.
Сколько лет сыновьям? (Ответ логичный и однозначный)
---
Дело в том, что и в задаче с голубями, и в задаче с сюрпризом Тиффани - участники владеют информацией, то есть себя надо на их место поставить и тогда все получится)
Bromka
Ну тут очевидное сообщение при уточнении, что
а) есть старший.
б) это не близнецы.
Следовательно, они разного возраста, и это подсказка. Надо взять квадраты чисел до 7 включительно, и посмотреть есть ли те, что укладываются в неоднозначное решение. Квадраты это 1, 4, 9, 16, 25, 36, 49, но неоднозначные из них только 4. Следовательно 1*4.
SalazarMAX
Задача ломается, если они всё-таки родились в один год (например, один в январе, а второй — в феврале).
t3sc0
и девять женщин родят ребенка за один месяц
SalazarMAX
Чёрт, хотел написать «второй в декабре», но что-то перемкнуло. Хотя в задаче не сказано, что оба ребёнка от одной матери :)
Kriminalist
Не понял, зачем брать квадраты.
Два сына дошкольника, значит, не более 6 лет каждому, значит, голубей не больше 6*6=12.
Из чисел от 1 до 12 можем сразу отбросить 7, 9 и 11 - 1*11, 1*9, 1*7 не подходят по критерию оба дошкольники, и являются простыми.
Также можем отбросить 1, 2, 3 и 5 - при таком количестве голубей информации было бы достаточно - числа простые, одна комбинация 1*х.
Что остается? 4, 6, 8, 10, 12.
10 = 10*1 (не подходит по дошкольнику) и 2*5 - информации достаточно, отбрасываем.
8 = 8*1 (не подходит по дошкольнику), = 4*4 - информации достаточно, отбрасываем
Остаются
12 = 12*1 (не подходит по дошкольнику), = 2*6 = 3*4 - 2 комбинации
6 = 1*6 = 2*3 - 2 комбинации
4 = 1*4 = 2*2 - 2 комбинации
Т.е. только при таких вариантах голубей информации недостаточно, чтобы определить возраст. Второй ответ дает достаточную информацию, а именно, что возраст неодинаковый. Это имеет ценность только для варианта 4 голубей, т.к. убирает один из вариантов (2*2), а для 12 и 6 голубей он не дает ничего - там и так нет одинаковых возрастов в сомножителях.
Можно еще рассмотреть вариант - 0 голубей.
В таком случае, одному нет года (0 лет), в второму от 1 до 6. Но тогда второй ответ не дает достаточной информации о возрасте второго ребенка.
Вариант с близнецами кстати мы отбросить не можем - есть же разнояйцевые, да и утверждение "старший похож на мать" не содержит отрицания, что младший не похож :).
Ну и в конце фраза все же должна звучать "теперь я знаю ответ на СВОЙ вопрос".
Bromka
Спасибо, что прислали нам доказательство
Великой теоремы Ферма. Первая ваша ошибка во втором предложении, 6*6 = 36, а не 12.Kriminalist
Спасибо, что заметили опечатку ). Хотя сути рассуждений это не меняет, просто удлиняет цепочку. Мое рассуждение с точки зрения второго математика, с квадратами опирается на послезнание второго ответа.
Bromka
Конечно. Но в моем случае перебрать достаточно только 6 чисел, а в вашем 36.
631052
все же не 36, а 21 вариант. ведь к примеру "6 и 4" и "4 и 6" - это один вариант, а не 2
Kriminalist
В вашем случае надо знать таблицу квадратов, а в моем решение способен отыскать даже школьник начальных классов вроде меня :)
Ente
Почему 1 и 6 не подходят? Произведение = 6, это также 2 * 3.
631052
потому что он "теперь знает". если было бы 6, он бы не знал, ведь при 6 имеем 2 варианта.
и если было бы 12, он тоже не знал бы, тоже 2 варианта.
а при 4 - только один вариант ("2 и 2" отброшен), поэтому знает.
значит 4 гульки и детям 1 и 4.
alan008
Странная, конечно, логика. Откуда же он знает, что "теперь знает" ответ? Это игра слов какая-то, а не реальное знание. Странно выводить сам ответ из слов, истинность которых говорящий не может проверить. Либо я что-то не так понял?
AkooF
Читайте внимательней задачу. Он как раз видит вокруг себя голубей и знает произведение. А вы, отгадывающий загадку - не видите голубей и можете только догадываться о их количестве. Вспомните, мы же не голубей считаем, а возраст детей вычисляем..
В этом взгляде со стороны на знания участников задачи и есть вся прелесть))
alan008
Спасибо за разъяснения!
iMoHax
Я вот тоже не понял, из чего он сделал вывод, что он теперь знает, у него же может быть все еще не полный набор информации.
Думаю не хватает еще одного вопроса, где ему сказали бы что дополнительной информации не требуется для решения. Либо что он знает ответ должен был сказать друг, а не он сам.
Тогда бы да, вывод был бы однозначным.
MiXei4
Потому что он видит, что у скамейки 4 голубя!
Произведение их возрастов равно 4.
Этой информации не достаточно, потому что есть 2 варианта 2 и 2, 1 и 4.
Один из них старше.
Понятно, не близнецы, 2 и 2 не подходит.
Exchan-ge
Решение с точки зрения гуманитария или инженера-практика:
1. Старший похож на мать (а не на отца)
2. Второй математик помнит (владеет информацией :), когда он встречался с женой первого
3. PROFIT! :)
631052
короче давайте заново.
вот возможные произведения сынов-дошкольников.
1*1=1
1*2=2
1*3=3
1*4=4
1*5=5
1*6=6
2*2=4
2*3=6
2*4=8
2*5=10
2*6=12
3*3=9
3*4=12
3*5=15
3*6=18
4*4=16
4*5=20
4*6=24
5*5=25
5*6=30
6*6=36
некоторые встречаются 1 раз, некоторые более 1-го раза.
более 1-го раза встречаются варианты 4, 6, 12.
раз инфы о произведении недостаточно, выбирать надо именно из этих 3х вариантов.
упоминание о старшем говорит о том, что они разного возраста.
остаются варианты:
1*4=4
1*6=6
2*3=6
3*4=12
2*6=12
теперь у второго инфы достаточно. значит, мы должны выбрать вариант произведения, который встречается ровно 1 раз.
такой вариант есть, и единственный - это 1 и 4. это и есть ответ.
задача, очевидно, на логику, а не на что-то другое.
поэтому нет нужны изобретать другие условия, что один родился в январе, а второй феврале, что они усыновленные, или что кто-то из них врет.
а так да, среди близнецов тоже есть старший, они же простигосподи не в обнимку выходят.
но задача ведь не об этом.