Ускоряем pow / forpes.ru

Главная
Ускоряем pow

Ускоряем pow +52

21.10.2021 01:15

alordash 32 11000 Источник

В этой статье я хочу поделиться несколькими нестандартными алгоритмами для быстрого возведения числа в степень, а также продемонстрировать их реализацию и сравнить их быстродействие в C++, C# и Java.

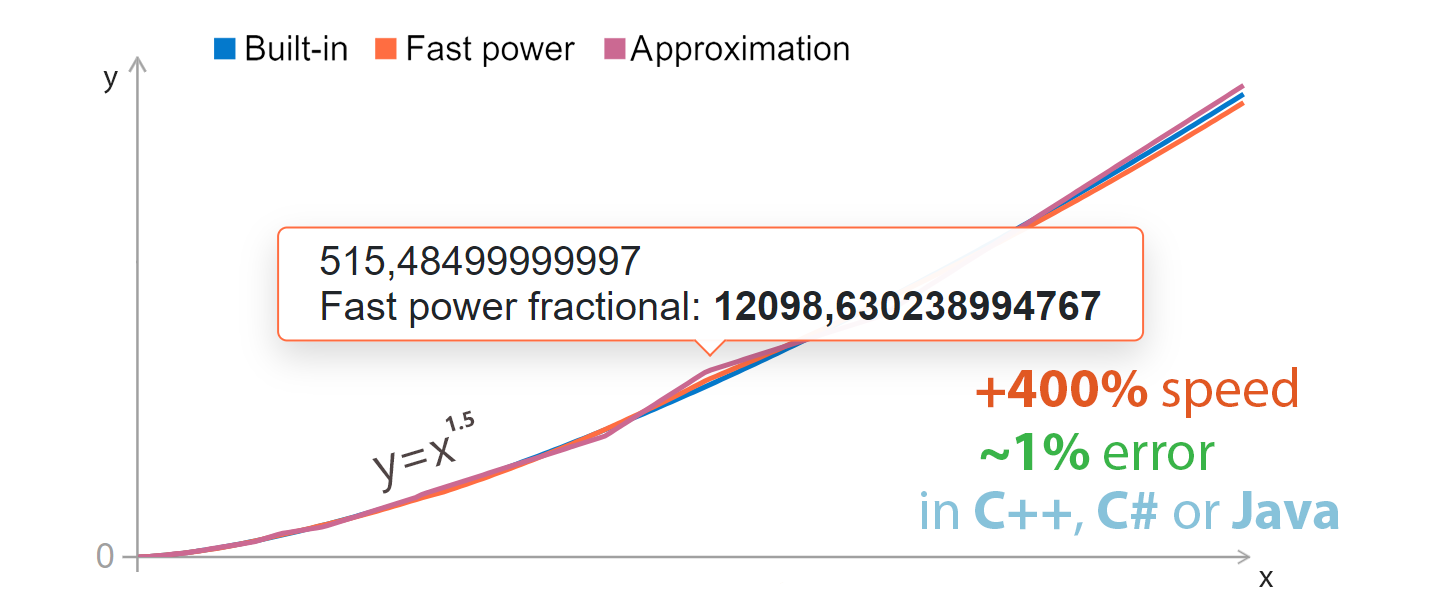
Сравнить точность алгоритмов можно прямо сейчас на этой странице.

В конце будет краткая памятка по тому, где и когда лучше применять какой из методов. При правильном выборе можно добиться увеличения скорости вычислений в 5 раз при погрешности ~1%, а иногда и вовсе без неё.

Содержание

Алгоритмы (5 штук)
Сравнение производительности
Сравнение точности
Вывод

На повестке дня у нас есть 5 алгоритмов: "Старая аппроксимация", "Бинарная степень", "Делящая быстрая степень", "Дробная” быстрая степень" и "Другая” аппроксимация".
Названия алгоритмам я придумал сам (за исключением бинарной степени), так как нигде не нашёл официальных версий, но вы можете называть их иначе.

Для расчета прироста скорости и погрешности будем сравнивать эти методы со стандартными функциями pow, Math.Pow и Math.pow в C++, C# и Java соответственно. О том, как производилось сравнение, будет сказано в частях “Сравнение производительности” и “Сравнение точности”.

Алгоритм: "Старая аппроксимация"

Увеличение скорости: в ~11 раз
Погрешность: <2%
Ограничения: приемлемая точность только для степеней от -1 до 1

Реализация в C++:

double OldApproximatePower(double b, double e) {
    union {
        double d;
        long long i;
    } u = { b };
    u.i = (long long)(4606853616395542500L + e * (u.i - 4606853616395542500L));
    return u.d;
}

Реализация в C# и Java

// C#
double OldApproximatePower(double b, double e) {
    long i = BitConverter.DoubleToInt64Bits(b);
    i = (long)(4606853616395542500L + e * (i - 4606853616395542500L));
    return BitConverter.Int64BitsToDouble(i);
}

// Java
double OldApproximatePower(double b, double e) {
    long i = Double.doubleToLongBits(b);
    i = (long)(4606853616395542500L + e * (i - 4606853616395542500L));
    return Double.longBitsToDouble(i);
}

Этот метод основан на алгоритме, использованном в игре Quake III Arena 2005 года. Он возводил число x в степень -0.5, т.е. находил значение: $\frac{1}{\sqrt{x}}$

Разработчики для этого написали такую функцию

float FastInvSqrt(float x) {
    float xhalf = 0.5f * x;
    int i = *(int*)&x;          // evil floating point bit level hacking
    i = 0x5f3759df - (i >> 1);  // what the fuck?
    x = *(float*)&i; 
    x = x*(1.5f-(xhalf*x*x));
    return x;
}

Узнал я об этом методе из статьи «Магическая константа» 0x5f3759df. В ней подробно объясняется как работает этот код и как его можно улучшить для работы с любой степенью и double’ми вместо float’ов. В моих кодах также есть магическая константа 4606853616395542500L. Нашёл я её по следующей формуле (она описана в статье выше):

//C# or Java
long doubleApproximator = (long)((1L << 52) * ((1L << 10) - 1.0730088));

Число 1.0730088 было подобрано вручную для достижения наибольшей точности вычислений.

Алгоритм: Бинарное возведение в степень

Увеличение скорости: в среднем в ~7.5 раз, преимущество сохраняется до возведения чисел в степень 134217728 в C++/C# и 4096 в Java.
Погрешность: нет, но стоит отметить, что операция умножения не ассоциативна для чисел с плавающей точкой, т.е. 1.21 * 1.21 не то же самое, что 1.1 * 1.1 * 1.1 * 1.1, однако при сравнении со стандартными функциями погрешности, как уже сказано ранее, не возникает.
Ограничения: степень должна быть целым числом не меньше 0

Реализация в C++:

double BinaryPower(double b, unsigned long long e) {
       double v = 1.0;
       while(e != 0) {
              if((e & 1) != 0) {
                     v *= b;
              }
              b *= b;
              e >>= 1;
       }
       return v;
}

Реализация в C# и Java

// C#
double BinaryPower(double b, UInt64 e) {
    double v = 1d;
    while(e != 0) {
        if((e & 1) != 0) {
            v *= b;
        }
        b *= b;
        e >>= 1;
    }
    return v;
}

// Java
double BinaryPower(double b, long e) {
       double v = 1d;
       while(e > 0) {
              if((e & 1) != 0) {
                     v *= b;
              }
              b *= b;
              e >>= 1;
       }
       return v;
}

Широко известный алгоритм для возведения любого числа в целую степень с абсолютной точностью. Принцип действия прост: есть целая степень e, чтобы получить число b в этой степени нужно возвести это число во все степени 1, 2, 4, … 2ⁿ (в коде этому соответствует b *= b), каждый раз сдвигая биты e вправо (e >>= 1) пока оно не равно 0 и тогда, когда последний бит e не равен нулю ((e & 1) != 0), домножать результат v на полученное b.
Пример: возвести 2 в степень 5.v = 1, e = 5 = 101₂, b = 2
Шаги цикла:

e = 101₂ - последний 1 → v *= b → v = 2
b *= b → b = 4
e >>= 1 → e = 10₂ = 2
e = 10₂ - последний 0 → пропускаем
b *= b → b = 16
e >>= 1 → e = 1
e = 1₂ - последний 1 → v *= b → v = 32
...
e = 0 → выход из цикла

Результат: v = 32, что и есть 2⁵.

Алгоритм: "Делящая быстрая степень"

Увеличение скорости: в ~3.5 раз
Погрешность: ~13%
Примечание: в коде ниже присутствуют проверки для особых входных данных. Без них код работает всего на 10% быстрее, но погрешность возрастает в десятки раз (особенно при использовании отрицательных степеней).

Реализация в C++:

double FastPowerDividing(double b, double e) {
       if(b == 1.0 || e == 0.0) {
              return 1.0;
       }
 
       double eAbs = fabs(e);
       double el = ceil(eAbs);
       double basePart = OldApproximatePower(b, eAbs / el);
       double result = BinaryPower(basePart, (long long)el);
 
       if(e < 0.0) {
              return 1.0 / result;
       }
       return result;
}

Реализация в C# и Java

// C#
double FastPowerDividing(double b, double e) {
       if(b == 1d || e == 0d) {
              return 1d;
       }
       var eAbs = Math.Abs(e);
       var el = Math.Ceiling(eAbs);
       var basePart = OldApproximatePower(b, eAbs / el);
       var result = BinaryPower(basePart, (long)el);
 
       if(e < 0d) {
              return 1d / result;
       }
       return result;
}

// Java
double FastPowerDividing(double b, double e) {
       if(b == 1d || e == 0d) {
              return 1d;
       }
       var eAbs = Math.abs(e);
       var el = Math.ceil(eAbs);
       var basePart = OldApproximatePower(b, eAbs / el);
       var result = BinaryPower(basePart, (long)el);
 
       if(e < 0d) {
              return 1d / result;
       }
       return result;
}

Узнав о методе аппроксимации чисел в степенях от -1 до 1 и о бинарном методе, мне захотелось объединить их для создания функции, которая могла бы быстро возводить число в любую степень. Для этого я придумал следующую формулу:

$el = \left | \left \lceil e \right \rceil \right |\\ x^e = (x^{\frac{e}{el}})^{el}$

Мы разбиваем степень на две части: e / el, которая всегда меньше или равна 1, и el, которая является целым числом. Теперь для расчета x^(e / el) мы можем использовать “старую” аппроксимацию, а для x^el - бинарную степень.Таким образом, объединяя этих два узкоспециализированных метода, мы получили универсальный метод. Но эту идею можно реализовать по-другому.

Алгоритм: "Дробная быстрая степень"

Увеличение скорости: в ~4.4 раза
Погрешность: ~0.7%

Реализация в C++:

double FastPowerFractional(double b, double e) {
       if(b == 1.0 || e == 0.0) {
              return 1.0;
       }
 
       double absExp = fabs(e);
       long long eIntPart = (long long)absExp;
       double eFractPart = absExp - eIntPart;
       double result = OldApproximatePower(b, eFractPart) * BinaryPower(b, eIntPart);
       if(e < 0.0) {
              return 1.0 / result;
       }
       return result;
}

Реализация в C# и Java

// C#
double FastPowerFractional(double b, double e) {
       if(b == 1d || e == 0d) {
              return 1d;
       }
 
       double absExp = Math.Abs(e);
       long eIntPart = (long)absExp;
       double eFractPart = absExp - eIntPart;
       double result = OldApproximatePower(b, eFractPart) * BinaryPower(b, eIntPart);
       if(e < 0d) {
              return 1d / result;
       }
       return result;
}

// Java
double FastPowerFractional(double b, double e) {
       if(b == 1d || e == 0d) {
              return 1d;
       }
 
       double absExp = Math.abs(e);
       long eIntPart = (long)absExp;
       double eFractPart = absExp - eIntPart;
       double result = OldApproximatePower(b, eFractPart) * BinaryPower(b, eIntPart);
       if(e < 0d) {
              return 1d / result;
       }
       return result;
}

По сути, любое число состоит из суммы двух частей: целой и дробной. Целую можно использовать для возведения основания в степень при помощи бинарного возведения, а дробную - при помощи “старой” аппроксимации.

В результате получаем следующую формулу:

$el = \left \lfloor e \right \rfloor\\ x^e = x^{el}*x^{e - el}$

Она, в отличии от формулы “делящего” метода, никак не искажает дробную часть. Это позволяет добиться намного большей точности.

Алгоритм: "Другая аппроксимация"

Увеличение скорости: в ~9 раз
Погрешность: <1.5%
Ограничения: точность стремительно падает при повышении абсолютного значения степени и остается приемлемой в промежутке [-10, 10]

Реализация в C++:

double AnotherApproximatePower(double a, double b) {
       union {
              double d;
              int x[2];
       } u = { a };
       u.x[1] = (int)(b * (u.x[1] - 1072632447) + 1072632447);
       u.x[0] = 0;
       return u.d;
}

Реализация в C# и Java

double AnotherApproxPower(double a, double b) {
       int tmp = (int)(BitConverter.DoubleToInt64Bits(a) >> 32);
       int tmp2 = (int)(b * (tmp - 1072632447) + 1072632447);
       return BitConverter.Int64BitsToDouble(((long)tmp2) << 32);
}

double AnotherApproxPower(double a, double b) {
       int tmp = (int)(Double.doubleToLongBits(a) >> 32);
       int tmp2 = (int)(b * (tmp - 1072632447) + 1072632447);
       return Double.longBitsToDouble(((long)tmp2) << 32);
}

Про историю этого алгоритма я ничего не знаю, я просто нашёл его тут: Optimized pow() approximation for Java, C / C++, and C#. Возможно, если использовать его в “делящей–” и “дробной быстрых степенях" вместо “старой” аппроксимации, можно достигнуть лучшей точности ценой немного меньшей скорости.

Сравнение производительности

Сравнение производительности производилось следующим образом: генерируем 500000 чисел-оснований в промежутке от 0.0 до 99999.0 и 500000 чисел-степеней в промежутке от A до B. Запоминаем текущее время, запускаем цикл на 500000 итераций, вычисляем значение основания в степени через функцию f и результат суммируем в calculationResult. По окончанию цикла снова замеряем время, разница во времени и есть время выполнения. Данная процедура повторяется 20 раз, конечный результат - усредненный за все 20 тестов.

Псевдокод сравнения производительности в C++:

(long long iterationsCount = 500000, double* bases, double* exps)
  double calculationResult = 0.0;
  double* base = bases;
  double* exp = exps;
  double* baseEnd = base + iterationsCount;
  auto start = std::chrono::high_resolution_clock::now();
  while(base < baseEnd) {
         calculationResult += f(*base++, *exp++);
  }
  auto finish = std::chrono::high_resolution_clock::now();
  auto time = std::chrono::duration_cast<std::chrono::nanoseconds>(finish - start).count();

Аналогично измерялась скорость в C# и Java. В репозитории проекта можно посмотреть на реальный код для сравнения производительности в C++, C# и Java.

Тесты производились в каждом языке для степеней в промежутках [-10.5, 0], [0, 2], [0, 10.5], [0, 25.75], [0, 55.5]. Прирост скорости каждого метода по сравнению со стандартным в каждом языке для каждого сета степеней изображен на графиках ниже:

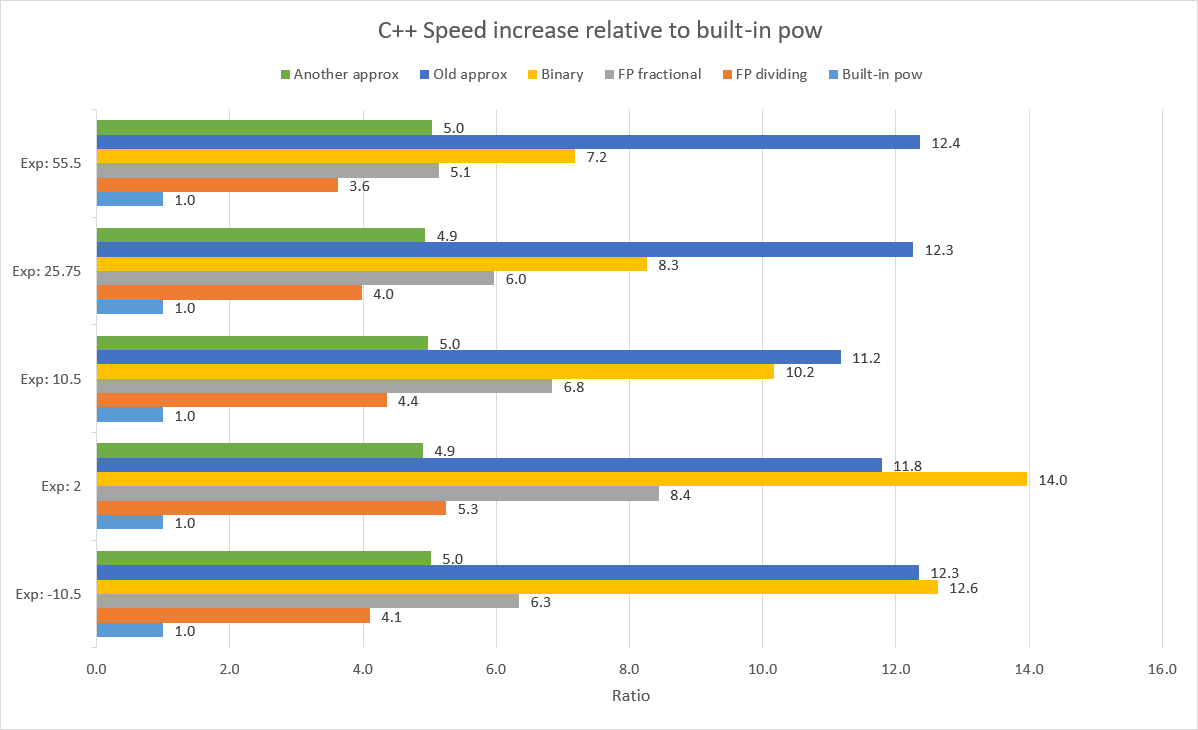
Рассмотреть подробнее результаты тестов можно посмотреть в этой таблице.

Тесты проводились на i5-10300H, 19.8 DDR4 GB usable RAM, 64-битная платформа.
C++: MSVC + /O2 + /Oi + /Ot
C#: optimize code

Сравнение точности

Для рассчитывания точности я возводил очередное число в определенную степень стандартным и одним из нестандартных способами, потом делил большее из полученных чисел на меньшее, складывал все эти отношения вместе, а в конце делил их на количество сравнений. Так и получалось значение погрешности.
Основания и степени генерировались также, как и в алгоритме сравнения производительности.
Для более гибкого и удобного тестирования я создал Blazor страницу, на которой можно построить графики реальных и полученных одним из методов значений чисел, лежащих в заданном промежутке и возведенных в указанную степень:

Ниже на этой же странице можно самим провести сравнение точности каждого метода для всех степеней, лежащих в заданном промежутке:

Вывод

Каждый из перечисленных мною методов дает различную точность и скорость. Поэтому, прежде чем использовать стандартную функцию возведения в степень, стоит проанализировать какие у вас будут входные данные, и насколько вам важна точность. Выбор правильного метода может существенно ускорить работу вашей программы. Чтобы сделать этот процесс проще, я подготовил вот такую шпаргалку:

Код всего проекта доступен на гитхабе. Там вы найдете и реализации всех алгоритмов в трех языках, и программы для сравнения точности для каждого языка, и код сайта.

Спасибо за внимание. Надеюсь эта статья поможет сделать ваш код немного быстрее.

Комментарии (32)

Refridgerator
21.10.2021 08:08
#23612892
Вместо бинарного возведения в степень можно использовать таблицу — она получается не такой уж и большой. Аппроксимацию значения экспоненты в диапазоне (0,1) можно получить с любой заданной точностью многочленами Чебышева.
1. Refridgerator
  21.10.2021 15:32
  #23614854
  +6
  Попробовал ради интереса на шарпе — получилось в 3 раза быстрее библиотечной и даже чуточку точнее.
  
  double[] powtable = {1,2,4,8,16,32, ..., 8.98846567431157954e307}; double pow2(double x) { bool sign = x < 0.0; x = sign ? -x : x; int xf = (int)x; x -= xf; double yt = powtable[xf]; double y = x * (0.6931471805599465398 + x * (0.2402265069590422222 + x * (0.05550410866590987068 + x * (0.00961812909717555934 + x * (0.0013333558738165095559 + x * (0.00015403509189194102748 + x * (0.000015253232908458899497 + x * (1.3207676270599404858e-6 + x * (1.0258347084283025531e-7 + (6.537941907237267033e-9 + 6.3026908837748924689e-10 * x) * x))))))))); return sign ? 1 / (y * yt + yt) : y * yt + yt; }
  
  UPD: Если ограничиться точностью single, то будет в 6 раз быстрее.
  double y = 2.5868889777e-9 + x * (0.693146928693029174 + x * (0.240230502044993504 +x * (0.0554804263257944027 + x * (0.00968458045229538239 + (0.0012387821479302309 + 0.000218775047688226791 * x) * x))));
  1. Refridgerator
    21.10.2021 17:45
    #23615430
    UPD: можно ускорить в 6 раз и без потери точности, если использовать ещё одну таблицу.
    
    Refridgerator
    22.10.2021 09:26
    #23617298
    Внезапно, с двумя таблицами результат оказался заметно менее точным, поэтому на практике предпочтительнее первоначальный вариант. Единственно, что после
    int xf = (int)x;
    
    не помешает добавить строчку
    if (xf >= 1024) return sign ? 0.0 : double.PositiveInfinity;
    
    tyomitch
    22.10.2021 11:26
    #23617722
    Пишите статью "Уточняем pow" :-)
    
    Refridgerator
    22.10.2021 13:42
    #23618346
    Думаю, что тут мы достигли теоретического предела. Единственная оставшаяся возможность — это считать всё на FPU с 80-битной точностью. Там и функция fscale есть для возведения двойки в целую степень, чтобы таблицу не городить.
    
    tyomitch
    22.10.2021 13:58
    #23618404
    Ээ, но ведь возведение двойки в целую степень — это (для double) просто сдвиг показателя степени на 52 бита влево? Для этого не нужно FPU.
    
    Refridgerator
    22.10.2021 14:37
    #23618580
    FPU нужен для 80-битной точности, а это значение всё равно в него нужно загружать. Возможно, такой фокус и в C# можно провернуть через BitConverter — не пробовал.
    
    Refridgerator
    23.10.2021 10:17
    #23621288
    +1
    Работает фокус:
    double yt = BitConverter.Int64BitsToDouble(((long)(1023 + xf) << 52));
    
    C# для неё нормальный код генерит:
    add edx,3FFh movsxd rdx,edx shl rdx,34h mov qword ptr [rsp],rdx vmovsd xmm1,qword ptr [rsp]
    
    tyomitch
    23.10.2021 11:18
    #23621462
    А как по скорости, в сравнении с таблицей?
    
    Refridgerator
    23.10.2021 11:36
    #23621522
    +1
    Чуть-чуть медленнее, 0.9855 от табличного. По сравнению с библиотечной получилось в 3.55 и 3.6 быстрее на Intel Core i5-5200U.

tyomitch
21.10.2021 08:40
#23612940
+14
Цитируемый код Q_rsqrt неполон без авторских комментариев, сохраняющих актуальность и при возведении в произвольную степень - "evil floating point bit level hacking" и "what the fuck?"
1. alordash Автор
  21.10.2021 11:49
  #23613760
  +9
  Совсем забыл добавить их, вернул. С ними сразу как-то понятней стало.

AVI-crak
21.10.2021 10:15
#23613240
+2
Странно заниматься ускорением функции pow без разбора exp и log.

KvanTTT
21.10.2021 16:01
#23614958
+1
У бинарного возведения в степень есть погрешность, потому что умножение не ассоциативно в поле чисел с плавающей точкой. x * x * x * x это не то же самое, что y = x * x, y * y.

Кстати, есть более эффективные небинарные возведения, например x ^ 6 — это y = x * x * x, y * y. В бинарном воведении переменных будет на 1 больше: y = x * x, z = y * y, z * y.
1. tyomitch
  21.10.2021 16:23
  #23615048
  Число переменных на эффективность не влияет, а попарных перемножений три что так что так.
  1. KvanTTT
    21.10.2021 17:21
    #23615334
    +2
    Число переменных может влиять на эффективность. Они могут не влезть во все регистры, особенно актуально для больших степеней.
    
    Более того, число умножений тоже может быть меньше, например для x^27:
    
    Тернарное умножение: 6 умножений, 2 переменных:
    y = x * x * x // 3 z = y * y * y // 9 result = z * z * z // 27
    
    Бинарное умножение: 7 умножений, 6 переменных:
    x1 = x * x // 2 x2 = x1 * x1 // 4 x3 = x2 * x2 // 8 x4 = x3 * x3 // 16 x5 = x4 * x3 // 24 x6 = x5 * x1 // 26 result = x6 * x // 27
    
    titbit
    25.10.2021 15:55
    #23628802
    А общая формула есть, чтобы вычислить оптимальное «небинарное» возведение в степень для степени N есть? Я как-то смотрел, но ничего кроме полного перебора вариантов не нашел.
    
    KvanTTT
    25.10.2021 16:09
    #23628864
    Интересный вопрос. Наверняка есть, подозреваю, что можно использовать динамическое программирование. Но такое лучше спрашивать у математиков, алгоритмистов. Попробую подумать на досуге.
    
    titbit
    26.10.2021 00:01
    #23630336
    Мне кажется есть аналогии с поиском оптимального алгоритма умножения через сдвиги и сложения (вычитания). Там приходится применять 3 алгоритма и выбирать лучший результат: схема Горнера, группировка бит (включая инверсную группировку), разложение на множители и рекурсивное применение поиска для множителей. Для степени я пробовал пойти похожим методом, но не знаю доказательств, что найденные последовательности действий минимальны.
1. alordash Автор
  21.10.2021 17:59
  #23615480
  Спасибо, что написали про ассоциативность, добавлю пометку.
  Однако на практике погрешности не возникает. Видимо, встроенные методы тоже подвержены этому эффекту (на скриншотах ниже погрешность отображается в столбце Sum difference).
  
  Тесты в C++
  Тесты в C#
  Тесты в Java
  Про способ с возведением через кубы я тоже думал. Было бы интересно посмотреть на программную реализацию троичного возведения в степень и сравнить его с другими методами.
  1. KvanTTT
    21.10.2021 18:04
    #23615506
    +1
    Однако на практике погрешности не возникает. Видимо, встроенные методы тоже подвержены этому
    
    А если сравнить с тупым перемножением? Его все равно не помешало бы добавить в таблицу для сравнения.
    
    Про способ с возведением через кубы я тоже думал. Было бы интересно посмотреть на программную реализацию троичного возведения в степень и сравнить его с другими методами.
    
    Там не совсем кубы, а в теории вообще обобщенное количество, которое на больших степенях может давать лучший результат. Но вроде такое разложение NP полное — его имеет смысл использовать разве что в генерации кода, но не в исполнении.
    
    qw1
    22.10.2021 12:03
    #23617888
    А если сравнить с тупым перемножением? Его все равно не помешало бы добавить в таблицу для сравнения.
    По идее, у «тупого перемножения» больше погрешность, чем у метода деления степени пополам, потому что намного больше операций (умножений), каждая из которых выполняется с погрешностью.
1. qw1
  22.10.2021 12:01
  #23617880
  Если посчитать число операций (умножений), то одинаково. Число переменных не важно, в цикле алгоритма они переиспользуются.

KvanTTT
21.10.2021 18:04
#23615504
<ошибся веткой>

sebres
21.10.2021 19:25
#23615784
Алгоритм: Бинарное возведение в степень ...
Погрешность: нет
Я бы не стал так категорично...
$ echo ' #include <stdio.h> #include <assert.h> #include <math.h> double BinaryPower(double b, unsigned long long e) { double v = 1.0; while (e) { if (e & 1) v *= b; b *= b; e >>= 1; } return v; } int main() { unsigned e = 134217728; double barr[] = {1.000001, 1.0000001, 1.00000001, 0}, *b = barr; while (*b) { printf("calc %.10g ** %u:\n fast pow ==> %.16f\n native ==> %.16f\n", *b, e, BinaryPower(*b, e), pow(*b,e)); b++; } return 0; } // ' > test.c; gcc -O2 -Wall -Wextra test.c -o test; ./test calc 1.000001 ** 134217728: - fast pow ==> 19497974326417947731259943008814618865863786077838628618240.0000000000000000 + native ==> 19497974384856317387011039256973190612600604089375799640064.0000000000000000 calc 1.0000001 ** 134217728: - fast pow ==> 674530.4760286132805049 + native ==> 674530.4755217875353992 calc 1.00000001 ** 134217728: - fast pow ==> 3.8273676342423024 + native ==> 3.8273676116718129
Как видим ошибка может быть довольно значительной, я уж не говорю про -Ofast (без -fno-fast-math).

Поправка: пример компилился в -m32toolchain... для -m64 погрешности действительно нет (по крайней мере на этих числах).
1. tyomitch
  21.10.2021 19:42
  #23615834
  По мнению WolframAlpha:
  1.94979745417325751802166478351188792876322264823289192517468 × 10^58
  674530.47074108455938268917802974681284444414341034203174237732783
  3.8273676654778624379533125217738601044713095101002538124954655334
  
  Т.е. разница между двумя реализациями pow не столь значительна, как разница между ними и точным результатом. В последнем случае «быстрая» реализация ещё и ближе к точному результату, чем «родная».
  1. sebres
    21.10.2021 20:14
    #23615922
    +1
    Ну у Wolfram precision и accuracy настраиваемые (если не ошибаюсь оно умеет длинную FP-арифметику, exact quantities и всё такое)...
    Пример алгоритма был для double (aka 64 bits IEEE normalized double-precision floating-point number) и C/C++...
    Я это о чем, собственно - что-то математически правильное (и доказуемо верное) в конкретной реализации на конкретном языке для какой-либо платформы может вылиться в неслабую такую погрешность (из-за переполнений, недостаточной precision промежуточных результатов и т.п.)...
    
    tyomitch
    21.10.2021 20:23
    #23615956
    Несомненно, что бинарное возведение в степень на практике даёт неточный результат.
    Я про другое: что «родная» pow даёт столь же неточный результат.
    
    sebres
    22.10.2021 14:24
    #23618514
    +1
    Несомненно, что бинарное возведение в степень на практике даёт неточный результат.
    
    Ну дак а я о чем, "Погрешность: нет" - как бы не совсем верно, если про этот алгоритм...
    
    Я про другое: что «родная» pow даёт столь же неточный результат.
    
    В рамках double - конечно.
    Я вам больше скажу, например тот же bigfloat.pow (даже с precision 400) также выдает "неточный" результат (и он менее точен чем нативный pow):
    
    bigfloat.pow, precision 400 ...
    >>> pow(1.000001, 134217728, precision(400)) BigFloat.exact('19497974326443151952384768395025354130242292944980784774315.431771682120918607912604365932634709150271941538088343395908095', precision=400) >>> pow(1.0000001, 134217728, precision(400)) BigFloat.exact('674530.47602706407027793197206421845263783142259940138702038470170721140355151884268337259494331459943481248761388507182459', precision=400) >>> pow(1.00000001, 134217728, precision(400)) BigFloat.exact('3.8273676342578585041456476752437466436493872281452027009938444315573508186002376274873069800877205918834944719451685524823', precision=400)
    Для сравнения возьмем корни от обоих (этот алгоритм у bigfloat насколько знаю точнее чем pow):
    
    bigfloat.root в сравнении с Wolfram ...
    >>> setcontext(precision(220)); p = getcontext().precision; >>> root(pow(1.000001, 134217728), 134217728) BigFloat.exact('1.0000009999999999177333620536956004798412322998046875000000000000000', precision=220) >>> root(BigFloat.exact('1.94979745417325751802166478351188792876322264823289192517468e58', precision=p), 134217728) BigFloat.exact('1.0000010000000000000000000000000000000000000000000000000000000000002', precision=220) >>> >>> root(pow(1.0000001, 134217728), 134217728) BigFloat.exact('1.0000001000000000583867176828789524734020233154296875000000000000000', precision=220) >>> root(BigFloat.exact('674530.47074108455938268917802974681284444414341034203174237732783', precision=p), 134217728) BigFloat.exact('1.0000001000000000000000000000000000000000000000000000000000000000003', precision=220) >>> >>> root(pow(1.00000001, 134217728), 134217728) BigFloat.exact('1.0000000099999999392252902907785028219223022460937500000000000000000', precision=220) >>> root(BigFloat.exact('3.8273676654778624379533125217738601044713095101002538124954655334', precision=p), 134217728) BigFloat.exact('1.0000000100000000000000000000000000000000000000000000000000000000001', precision=220)
    Но если округлить результаты до оригинальной accuracy - то все результаты верны.
    Что не отменяет факт, что результат pow может сильно отличатся и погрешность есть, хоть и небольшая - для bigfloat.pow (и BinaryPower) около 11.04e-7%, а для pow - 08.04e-7%, что очень неплохо для степени 134217728.
    
    │ algorithm │ error % │ ├──────────────┼───────────────┤ │ BinaryPower | 0.0000011043% │ │ bigfloat.pow │ 0.0000011042% │ │ native pow │ 0.0000008045% │

iShrimp
22.10.2021 20:30
#23620024
+1
А можно ли улучшить "грубый" результат каким-либо алгоритмом уточнения корня (как это делается для быстрого обратного квадратного корня)?
1. alordash Автор
  23.10.2021 22:06
  #23623352
  Боюсь, что уточнение результата так же, как и в алгоритме быстрого обратного корня, для произвольной степени будет не оптимально. В быстром обратном корне используется метод Ньютона, который использует производную от изначальной функции. А у нас функция вида , так что её производная будет $f'(x)=nx^{n-1}$ , что также содержит в себе степень. Получается, что нам придется помимо того, что возводитьв степень, также возводитьв степень, для чего снова придется использовать один из быстрых алгоритмов, который будет снова использовать себя, и так далее, пока не дойдем до какой-то степени, которую можно посчитать за один такт.
  По поводу других методов уточнения результата ничего сказать не могу, не изучал эту тему.

Ускоряем pow +52

Содержание

Алгоритм: "Старая аппроксимация"

Алгоритм: Бинарное возведение в степень

Алгоритм: "Делящая быстрая степень"

Алгоритм: "Дробная быстрая степень"

Алгоритм: "Другая аппроксимация"

Сравнение производительности

Сравнение точности

Вывод

Комментарии (32)

alordash Автор

alordash Автор

alordash Автор