14.12.2021 14:16
iapetus2 1 1700 Источник

Привет всем хабровчанам и просто заглянувшим!

Поддавшись осенне-зимнему тренду на Хабре на (около)криптографические статьи, я решил поддержать оный, потому что чем больше годной информации на русском, тем лучше-ж, да..?
Итак, сегодня я хочу рассказать вам о Blue Midnight Wish (BMW, да-да, может кто-то еще не понял). Сразу хочу предупредить - это моя первая статья, поэтому будьте нежнее, по возможности...

Краткий экскурс в контекст

В 2007 году Национальным институтом стандартов и технологий (NIST) был объявлен конкурс на создание нового криптоалгоритма для замены SHA-1 и SHA-2, по итогам которого должен был быть избран алгоритм для SHA-3. Blue Midnight Wish был одним из предложенных алгоритмов, успешно прошедшим первый тур отбора.

Для тех кто хотя бы слегка в курсе освещаемой темы, милости прошу к следующему параграфу, а остальным предлагаю пробежаться по основным понятиям, которые будут использоваться дальше:

Шпаргалка

Хэш-функция - это любая функция, которая может использоваться для отображения данных произвольного размера в значения фиксированного размера. Значения, возвращаемые хэш-функцией, называются хэш-значениями, хэш-кодами, дайджестами или просто хэшами. При построении хэш-функции стараются минимизировать число коллизий, оптимизировать скорость работы и уменьшить потребляемые ресурсы.

Существует класс хэш-функций, используемых в криптографии - собственно криптографические хэш-функции. Их отличает криптостойкость, BMW - это криптографическая хэш-функция.

SHA (Secure Hash Algorithm) - алгоритм безопасного хэширования, на данный момент (декабрь 2021) насчитывает четыре поколения, последнее это SHA-3.

Необходимые далее обозначения

H

Двойная трубка(double pipe, dp). Изменяющееся значение, которое минимум в два раза шире, чем конечная цифровая подпись в n бит

Q

Счетверенная трубка(quadruple pipe, qp) - аналогично, но уже вчетверо

H^{(i)}

i-е значение dp, H^{(0)}— начальное значение.

Q^{(i)}

i-е значение qp.

H_j^{(i)}

j-е слово из H^{(i)}Где H^{(i)}разбивается на заранее определённое количество блоков - слова

Q_j^{(i)}

j-е слово qp Q^{(i)}

Q_a^{(i)}

Первые 16 слов из Q^{(i)}

Q_b^{(i)}

Последние 16 слов из Q^{(i)}

M

Сообщение

Что там инженеры наинженерили...

Для ясности

Если описывать алгоритм максимально ёмко, то выйдет что-то вроде
Сообщение M делим на N m-битных блоков и далее

i = 0
while(i < N) {
   Q_a(i) = f0(M(i), H(i-1))
   Q_b(i) = f1(M(i), Q_a(i))
   Q(i) = Q_a(i) concate Q_b(i)
   H(i) = f2(M(i), Q(i))
   i++
 }
 Q_a(final) = f0(H(N), const)
 Q_b(final) = f1(H(N), const, Q_a(final))
 H(final) = f2(H(N), Q_a(final), Q_b(final)
 
 hash = N_Least_Significant_Bits(H(final))

В целом дальше в статье я буду распространяться про все обозначения из этих 13 (тут от страха мог умереть один американец) строчек кода.

Blue Midnight Wish следует общему шаблону проектирования большинства хэш-функций.
Два основных этапа:

  1. Первичная обработка

    (а) заполнение сообщения (padding),

    (б) разбиение сообщения на m-битные блоки (parsing),

    (в) установка начальных значений, которые будут использоваться при вычислении хэша

  2. Вычисление хэша

    (а) создание расписания сообщений (message schedule) из дополненного сообщения,

    (б) использование этого расписания вместе с функциями, константами и операциями со словами для итеративного создания серии значений двойной трубки,

    (в) окончательное значение двойной трубки, сгенерированное итеративным процессом в (б) используется в качестве входных данных для функции финализации (определим ее далее);

    (г) n последних значащих бит функции финализации используются для расчета хэша сообщения.

Размеры блоков и слов зависят от конкретной реализации алгоритма BMW, привожу их в таблице:

версия алгоритма

размерpсообщения, бит

размерmблока, бит

размерwслова, бит

размерnхэша, бит

BMW224

< 2^{64}

512

32

224

BMW256

< 2^{64}

512

32

256

BMW384

< 2^{64}

1024

64

384

BMW512

< 2^{64}

1024

64

512

Далее в статье подробнее разберу весь алгоритм по шагам на примере BMW256.

Заполняем сообщение

Предположим, что длина сообщенияMравнаp бит. Добавляем единичный бит в конец сообщения, далееkнулевых бит, где k- наименьшее неотрицательное решение уравнения p + k + 1 \equiv 448\pmod{512}. Затем добавляется 64-битный блок, равный числу p, выраженному с помощью его двоичного представления.

Например, сообщение "habr", закодированное в 8-битном ASCII, имеет длину 8 \times 4 = 32, поэтому сообщение дополняется битом «1», затем 448 - (32 + 1) = 415нулевыми битами и затем 64-битным двоичным представлением числа 32, чтобы стать 512-битным дополненным сообщением.

\overbrace{\overbrace{01101000}^{"h"} \space \overbrace{01100001}^{"a"} \space\overbrace{01100010}^{"b"} \space\overbrace{01110010}^{"r"}\space1\underbrace{00...0}_{415}\underbrace{00...0\overbrace{100000}^{p=32}}_{64}}^{512\space бит}

Разбиваем сообщение на блоки

После того, как сообщение было дополнено, оно должно быть разбито наNm-битовых блоков перед вычислением хэша.

Для BMW256 дополненное сообщение разбирается наN512-битных блоков, M_1, M_2, ..., M_N. Поскольку 512 бит входного блока могут быть выражены шестнадцатью 32-битными словами, первые 32 бита блока сообщенияiобозначаютсяM_0^{(i)}, следующие 32 бита -M_1^{(i)}и так далее доM_{15}^{(i)}.

Из-за того, что BMW имеет обратный (little-endian) порядок байтов, обратите внимание на обратный порядок байтов в M_i.

Для нашего сообщения "habr":

M_0 = 0х72626168

M_8= \space0х00000000

M_1= 0х00000080

M_9= \space0х00000000

M_2= 0х00000000

M_{10}= 0х00000000

M_3= 0х00000000

M_{11}= 0х00000000

M_4= 0х00000000

M_{12}= 0х00000000

M_5= 0х00000000

M_{13}= 0х00000000

M_6= 0х00000000

M_{14}= 0х02000000

M_7= 0х00000000

M_{15}= 0х00000000

Начальное значение двойной трубки

Перед началом вычисления хэш-функции для каждого из хэш-алгоритмов должно быть установлено начальное значение dp - H^{(0)}. Размер и значение слов в H^{(0)}зависят от размера дайджеста сообщенияn. H^{(0)}для BMW256 начинается с байта 0x40 и принимает все 64 последовательных байтовых значения до 0x7F.H^{(0)}должно состоять из шестнадцати 32-битных слов.

Значение itself:


H^{(0)}=0х40414243\space0х44454647\space0х48494a4b\space0х4c4d4e4f\\ \space0х50515253\space0х54555657\space0х58595a5b\space0х5c5d5e5f\\\space0х60616263\space0х64656667\space0х68696a6b\space0х6c6d6e6f\\\space0х70717273\space0х74757677\space0х78797a7b\space0х7c7d7e7f

Непосредственно алгоритм хэширования

BMW256 может использоваться для хэширования сообщенияMдлинойpбит, где 0<p<2^{64}. Алгоритм использует

  1. шестнадцать 32-битных слов которые являются частью двойной трубки;

  2. дополнительные шестнадцать 32-битных слов, которые вместе со словами двойной трубки образуют счетверённую трубку;

  3. два временных 32-битных слова XLи XH.

Слова счетверённой трубки обозначены какQ_0^{(i)},Q_1^{(i)},...,Q_{31}^{(i)}. Слова двойной трубки обозначенные как H_0^{(i-1)},H_1^{(i-1)},...,H_{15}^{(i-1)}, изначально хранят значение H^{(0)}, которое далее итерационно заменяется промежуточным значением двойной трубки (после обработки каждого блока сообщения), окончательно будут хранить значение двойной трубки H^{(N)}.

Мы используем три функции:

f_0:\{0,1\}^{2m} \rightarrow \{0,1\}^m\\f_1:\{0,1\}^{3m}\rightarrow\{0,1\}^m \spaceи \space Q_b^{(i)} = f_1(M^{(i)}, H^{(i-1)},Q_a^{(i)})\\f_2:\{0,1\}^{3m}\rightarrow\{0,1\}^m \spaceи\space H^{(i)}=f_2(M^{(i)}, Q^{(i)}) \equiv f_2(M^{(i)},Q_a^{(i)},Q_b^{(i)})

1. f_0 принимает 2 аргумента - M^{(i)}и H^{(i-1)}каждый из m битов, и для любого значения H^{(i-1)}(текущее значение dp) она биективно преобразует M^{(i)}(i-й блок сообщения). Результат

Q_a^{(i)} = f_0(M^{(i)}, H^{(i-1)})=A_2(A_1(M^{(i)}\oplus H^{(i-1)})) + ROTL^1(H^{(i-1)})

является первой частью счетверённой трубки.

2. Вторая функция f_1принимает три аргумента: блокM^{(i)}из m битов, текущее значение dpH^{(i-1)}и значение Q_a^{(i)}(первая часть qp), чтобы вычислить вторую часть Q_b^{(i)}=(Q_{16}^{(i)}, Q_{17}^{(i)}, ...,Q_{31}^{(i)}) cчетверённой трубы qp. Эта функция для каждогоH^{(i-1)}делает следующее: для данной пары (M^{(i)},Q_a^{(i)})однозначно вычисляет Q_b^{(i)}, затем для данной пары (M^{(i)},Q_b^{(i)})однозначно вычисляет Q_a^{(i)}и для данной пары (Q_a^{(i)},Q_b^{(i)})она однозначно вычисляет M^{(i)}.

3. f_2отображает 3m бит в m бит. Она принимает два аргумента: блок M^{(i)}размером m бит и текущее значение Q^{(i)}=(Q_a^{(i)},Q_b^{(i)})размером 2m бит, чтобы создать новую двойную трубку H^{(i)}из m бит.

Конечным результатом BMW256 является 256-битный хэш, который представляет собой 256 младших значащих битов из окончательного хэш-значения H^{final}, то есть значений (H_8^{final},H_9^{final},...,H_{15}^{final}).

Пояснение для тех, кто еще не потерялся

ПреобразованияA1\space и \space A2, как и конкретную реализацию алгоритма я позволю себе определить картинками из документации IEEE чуть ниже (простите, простите, простите), для любознательных ссылка (на IEEE);

\oplus- операция XOR

ROTL^1(H^{(i-1)})=(H_1^{(i-1)}, H_2^{(i-1)}, ...,H_{15}^{(i-1)}, H_0^{(i-1)})циклически переставляет первый элемент вектора H^{(i-1)}в конец.

SHR^r(x) - сдвиг вправо на r бит слова x

SHL^r(x) - сдвиг влево на r бит слова x

Функция f_0 представляет собой композицию преобразований A_1 \space и \space A_2

Преобразования A1 и A2 соответственно, их композиция - функция f0
Преобразования A1 и A2 соответственно, их композиция - функция f0
Вычисление вспомогательных функций expand
Вычисление вспомогательных функций expand

Для определения функции f_1еще разок воспользуемся псевдокодом, ExpandRounds_1 и \space ExpandRounds_2 - известные выбранные параметры

f1:
for ii = 0 to ExpandRounds_1 - 1 do:
Q(ii+16, i) = expand_1(ii + 16)
for ii = ExpandRounds_1 to ExpandRounds_1 + ExpandRounds_2 - 1 do:
Q(ii+16, i) = expand_2(ii + 16)

Функция f_2задается следующим образом:

Вычисляются XL \space и \space XH

XL=Q_{16}^{(i)}\oplus Q_{17}^{(i)}\oplus ...\oplus Q_{23}^{(i)}\\XH= XL \oplus Q_{24}^{(i)} \oplus Q_{25}^{(i)} \oplus...\oplus Q_{31}^{(i)}

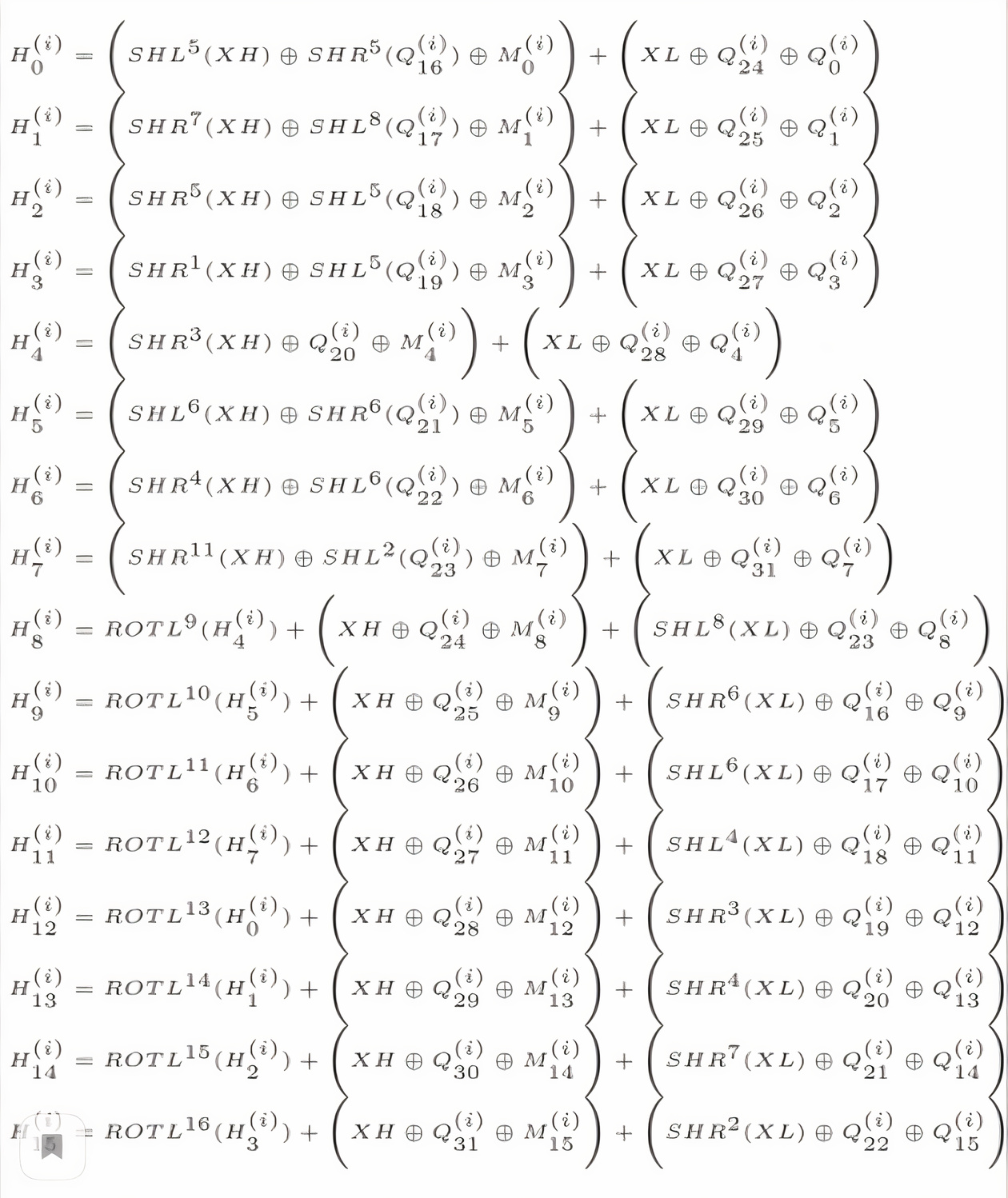
Итеративное вычисление нового значения dp - функция f2
Итеративное вычисление нового значения dp - функция f2

Заключение

Алгоритм Blue Midnight Wish достойно показал себя в конкурсе NIST, но в конечном итоге уступил алгоритму Keccak. Причиной стала возможная уязвимость к псевдо-коллизионным атакам.
Такие структуры как BMW, на мой взгляд, заставляют хотя бы проникнуться уважением к труду тех кто угрохал много сил на свое дело на своем примере показывают, что темпы развития технологий сейчас поражают воображение, реально применяется о-малое от создаваемых решений и алгоритмов, при высокой доле отсеивания хороших вариантов, чтобы в конечном счете найти лучший.

Эта статья проба пера и введение к циклу, в скором времени для большей наглядности завезу реализацию BMW и нескольких других алгоритмов участников SHA-3, следите за обновлениями.

Большое спасибо что прочитали, мне очень приятно видеть это:)

Источники

  1. Danilo Gligoroski, Vlastimil Klima, Svein Johan Knapskog, Mohamed El-Hadedy, Jørn Amundsen, Stig Frode Mjølsnes. Blue Midnight Wish. // Trondheim, Norway: Norwegian University of Science and Technology, 2008. — С. 71.

  2. https://ieeexplore.ieee.org/document/5683052 - документация с IEEE.

  3. Soren S. Thomsen. Pseudo-cryptanalysis of Blue Midnight Wish. — 2009. — С. 7.

Комментарии (1)


  1. Shaman_RSHU
    15.12.2021 10:45
    #23822821
    +1

    Колитесь, в каком ВУЗе Вас заставляют писать сюда такие статьи? На каком курсе, по какому предмету? :)

    В песочнице на очереди выстроилось несколько статей подобной тематики.