Пространство плоскости часто делят на квадраты. Или, наоборот, квадратные вещи собирают вместе. Наверняка у кого-нибудь уже возникала идея собрать гирлянду из квадратных светильников и с помощью неё заполнить светом фигуру выбранной формы, с квадратными элементами детализации, как пикселями. Такой квадратный светильник может быть устроен так, что с предыдущим и следующим светильником соединён углами одного ребра.



Достаточно хорошо известен способ расположить светильники так, что у соседних на плоскости элементов будут все шансы оказаться рядом и в самой гирлянде. Последовательность расположения должна вихлять туда сюда, на любом этапе представлять собой достаточно компактное пятно. Порядок расположения центров проходит по кривой Гильберта.

Логика построения такая: расстановку в виде квадрата 2 на 2, нужно представить как один большой светильник и составить из него светильник ещё больше. Именно поэтому, если у вас на каком-то этапе получается квадрат, то его размер кратен степени двойки.


Алгоритм построения: при масштабировании петля «a» заменяется на последовательность
"+bs-asa-sb+", где +/− это повороты, s — это шаг вперёд. Петля «b» заменяется на "-as+bsb+sa-".

Для представления координат в такой расстановке кроме обычного кода можно использовать код Грея, который получается побитовым XOR обычного кода с числом, которое сдвинуто на один бит в сторону уменьшения. При изменении на единицу в этом коде всегда меняется только один бит. А именно, тот который в обычном коде делит биты на изменившиеся в результате лавины переноса и не изменившиеся.

По порядку: бинарный код, код Грея, различие битов с предыдущим числом, номер отличающегося бита.



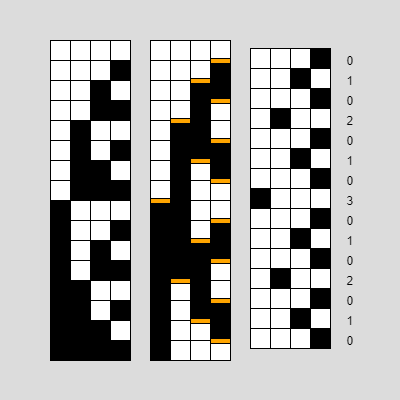
Для декодирования можно заметить, что у младшего, последнего бита есть зависимость результата сразу от всех битов кода. У предпоследнего бита результата зависимость от всех битов, кроме последнего, и так далее со всеми. Значит, вычислять удобнее начиная с первого, с использованием «бита текущей зависимости», совмещающего последовательно через XOR каждый из перебираемых бит, и так дойти до последнего.

Если обе координаты на плоскости закодировать этим кодом, то можно обнаружить, что так как все шаги единичные и направлены всегда вдоль одной из осей, то каждый шаг продолжает менять координаты только на один бит. И, например, одна «петля» как бы заменяет один шаг тремя, в кодах это выглядит как указание к изменению одного и того же бита, но происходит до и после переключения дополнительного бита. Такой принцип прохода можно расширить на любое количество координат.



На этом изображении показано битовое представление координат. В первой колонке биты сначала для x, затем для y. Во второй колонке биты вперемежку. Третья колонка представляет координаты в кодах Грея. Четвёртая колонка показывает изменившийся бит.

У такой расстановки нет центрального светильника, в центре всего квадрата будет лишь узел соединения. А что если у вас светильников в гирлянде пять штук? Можно ли построить симметричную схему? Оказывается, да, один из симметричных вариантов расстановки состоит из пяти квадратов. Оказывается, последовательную гирлянду можно сложить в крест, c центральным элементом.



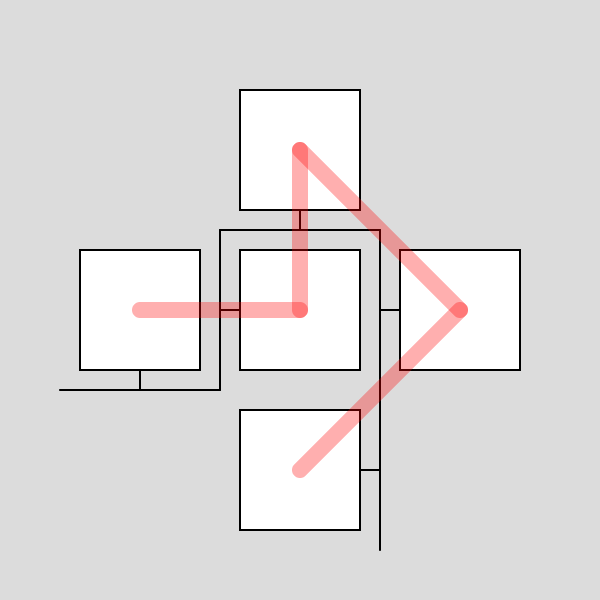
Более того, сам такой крест представляет собой светильник, который можно принять за элемент, и в итоге построить крест из крестов из двадцати пяти светильников.



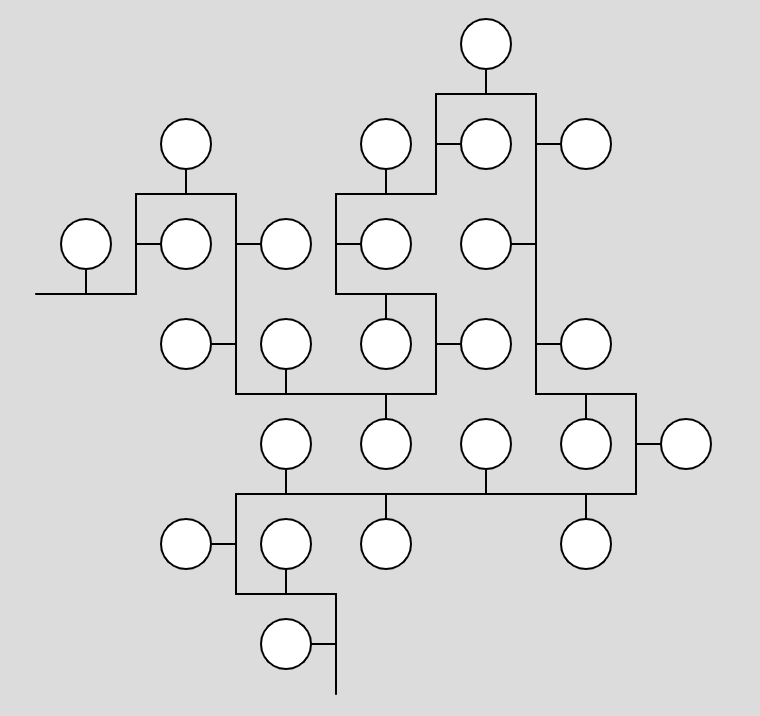
В кривой Гильберта соединение линии происходит между центрами элементов, а здесь линию из горизонтальных и вертикальных шагов составляет линия проходящая по ребру.



Фигура из таких пикселей получается немного не квадратной.

Не знаю, можно ли обобщить это на большую размерность, но такая расстановка не менее интересна, чем расстановка по кривой Гилберта.

Если обозначить расположение центра светильника относительно идущего вперёд края — слева «a», а справа «b», то один шаг изменения масштаба будет представлен так:

a -> a , b+, a, a-, b-
b -> a-, b-, b, a+, a

Где + и − обозначают изменение направления относительно общего, разворот одного элемента на прямой угол вправо или влево. Интересно, что средний элемент своим кодом совпадает с общим элементом, но центр креста кодируется у «a» вторым элементом, у «b» четвёртым.



Добавлен ещё один уровень масштабирования.

Какие-то интересные светлые линии проявились, без явного паттерна.



Они образовались потому что в каждый «узел» связи линии подведены ровно два фрагмента, а значит ровно два — не проведены. При переключении для каждого узла между проведёнными и не проведёнными появляется парная линия. Впрочем, не факт, что на всю плоскость она одна.

***

Вот и всё о двух способах прохода. Теперь можно отвлечься и проверить, сколько же отдельных линий-макаронин в эту лапшу уместилось.

***

Примем центральный крест за начальный, чтобы во время масштабирования просто добавлять новые кресты вокруг.



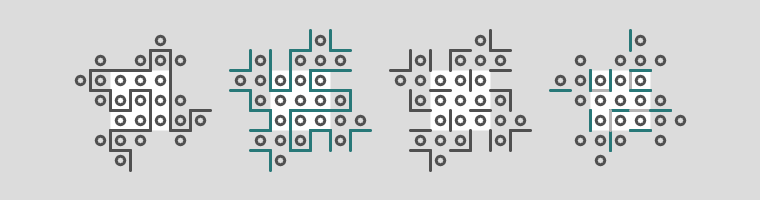
Здесь показаны:

• Оригинальная линия.
• Парная линия, которую исследуем.
• Фрагменты, которые не зависят от поворота.
• Фрагменты, которые зависят от поворота.

Дальше можно соотнести положение креста первого уровня с крестами второго уровня, следя за фрагментом линии. И расставить сразу на третий уровень.



Если проследить за линиями третьего уровня, окажется, что есть три типа линий: линии идущие по контуру, две линии, которые так же имеют концы на контуре, но погружаются внутрь фигуры. И одна линия, которая делит фигуру, и остальные части находятся по обе стороны от неё. Линия проходит через центр всего креста.

Сначала я предполагал, что при расширении останется три линии, проходящие через центр. И множество остальных, появляющихся при расширении области. Но ещё на третьем уровне видно, что один из фрагментов соединяется с центральной линией.



А после анализа четвёртого уровня становится ясно, что все дополнительные линии с ней тоже соединены. Поэтому линия всего одна, в виде чуть усложнённой двойной спирали.

Получилось даже три вида последовательного перебора пикселей на плоскости. А упрощённая схема четвёртого уровня даёт четвёртый вид, для которого можно и свою парную линию построить.

Пожалуй, так и оставлю два вида: ламповые и не ламповые.

---

Принимается донат.