Ряд Тейлора для функции представляет собой бесконечную сумму членов, которая использует информацию о производных этой функции для создания полинома, аппроксимирующего эту функцию. Более точные аппроксимации можно вывести, взяв производные более высокого порядка и используя полиномы более высокой степени. В интернете уже есть много статей (и видео на YouTube) о рядах Тейлора, которые помогут вам сформировать хорошее понимание процесса построения бесконечного ряда с упоминанием того, как члены более высоких порядков дают вам более близкие аппроксимации базовой функции (при условии, что ряд сходится). Тем не менее, таких, которые наглядно демонстрируют, почему это может быть так важно для нас, не очень много.

Когда я впервые столкнулся с рядами Тейлора в рамках своего бакалаврского курса, особого впечатления они на меня не произвели — я отнесся к ним как к вполне себе рядовой теме. Но недавно, готовясь к GRE Mathematics Subject Test, я наконец проникся и решил реализовать их на Python. Эта реализация требует от нас только определить аппроксимируемую функцию, все остальное обрабатывается численно. В этой статье мы рассмотрим реализацию ряда Тейлора на Python и обсудим некоторые потенциальные варианты его использования.

Реализация

Членам ряда Тейлора функции f(x) требуются производные последовательно более высоких порядков f^(n)(x) — для определения коэффициентов полинома. Следовательно, ряд Тейлора может быть определен для f(x), только если она бесконечно дифференцируема. Члены ряда определяются выражением

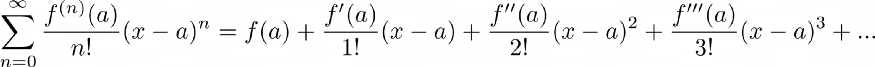
Где а является центром ряда Тейлора (прим. ред.: этот термин используется англоязычным сообществом, а русскоязычное в основном оперирует окрестностью точки а). Если центр ряда равен 0, т. е. a=0, то ряд называют рядом Маклорена.

Чтобы программно сформировать ряд Тейлора для функции, все, что от нас требуется, это вычислить коэффициенты

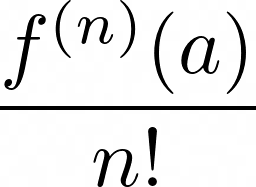
для достаточного количества членов. Опять же напомню, что чем больше членов ряда Тейлора мы будем использовать, тем точнее будет аппроксимация. К счастью, в пакете Python scipy уже есть встроенная функция для вычисления производной функции в заданной точке. Именно ее мы и будем использовать для определения коэффициентов искомого полинома.

from scipy.misc import derivative
import math

class TaylorSeries():
    def __init__(self, function, order, center=0):
        self.center = center
        self.f = function 
        self.order = order
        self.d_pts = order*2
        self.coefficients = []

        # количество точек (order) для scipy.misc.derivative
        if self.d_pts % 2 == 0: # must be odd and greater than derivative order
            self.d_pts += 1

        self.__find_coefficients()

    def __find_coefficients(self):
        for i in range(0, self.order+1):
            self.coefficients.append(round(derivative(self.f, self.center, n=i, order=self.d_pts)/math.factorial(i), 5))

Приведенная выше логика начинается с определения класса для хранения информации о ряде Тейлора. Конструктор принимает указатель на функцию (function) для которой мы формируем ряд Тейлора, порядок (order) ряда Тейлора (то есть количество членов) и центр (center) ряда, который по умолчанию соответствует ряду Маклорена (т.е. равен нулю). Некоторые переменные, которые используются в функции scipy.misc.derivative, вычисляются на лету из уже предоставленных нами данных. А затем сразу же вызывается приватный метод __find_coefficients(…) для определения значений коэффициентов для каждого члена нашего ряда Тейлора. Это делается программно, путем определения производных для каждого члена ряда Тейлора и деления на соответствующий факториал, как было показано выше.

По сути, это практически все, что нам нужно сделать для получения ряда Тейлора в Python. Остальные взаимодействия с рядом Тейлора будут просто использовать эти коэффициенты. Прежде чем углубиться в них, давайте проверим, что этот код работает, определив коэффициенты некоторых полиномов (рядов Тейлора для конкретных функций). Чтобы можно было проверить результаты, мы определим две функции для просмотра коэффициентов и результирующего уравнения, представляющего ряд Тейлора.

def print_equation(self):
    eqn_string = ""
    for i in range(self.order + 1):
        if self.coefficients[i] != 0:
            eqn_string += str(self.coefficients[i]) + ("(x-{})^{}".format(self.center, i) if i > 0 else "") + " + "
    eqn_string = eqn_string[:-3] if eqn_string.endswith(" + ") else eqn_string
    print(eqn_string)

def print_coefficients(self):
    print(self.coefficients)

def get_coefficients(self):
    """
        Возвращает коэффициенты ряда Тейлора
    """
    return self.coefficients

Первая функция, print_equation(…), выводит ряд Тейлора как уравнение с центром в центре ряда. print_coefficients(…) просто выведет список с коэффициентами, а get_coefficients(…) вернет его.

Приведенный ниже код используется для нахождения коэффициентов ряда Тейлора, представляющего функцию f(x):

from TaylorSeries import TaylorSeries

def f(x):
    return 2 + x**3 + x**7 + x**2

if __name__ == '__main__':
    terms = 15
    center = 0
    precision = 3

    ts = TaylorSeries(f, terms, center)
    ts.print_coefficients()
    ts.print_equation()

Выполнение этой логики сформирует список размером в 15 элементов, который содержит коэффициенты ряда Тейлора, а также выведет полиномиальное уравнение. В этом случае функция “аппроксимируется” рядом Тейлора из 15 параметров

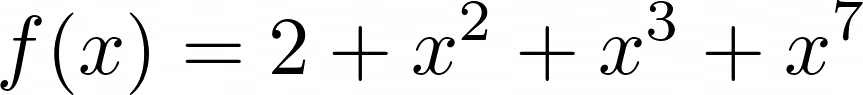
Поскольку это полином, ряд Тейлора должен точно представлять его, имея первый коэффициент (константу) 2.0, коэффициенты 1.0 для индексов 2, 3 и 7 и коэффициенты 0.0 во всех остальных порядков. Т.е. мы получим многочлен, показанный выше. И действительно, запуск скрипта дает нам следующий вывод:

Изменение функции f(x) на различные полиномы в приведенном выше Python-скрипте дало те же результаты — каждый полином точно представлен рядом Тейлора. Это не очень увлекательно, но это хороший способ убедиться, что логика работает должным образом. Более интересные функции, благодаря аппроксимации которых ряд Тейлора получил широкую известность, например, sin(x), cos(x), e^x и т. д., также дают правильные результаты в этой реализации. Далее, в приведенных ниже применениях, мы будем использовать именно эти функции.

Применения ряда Тейлора

Поскольку с полиномами обычно легче работать, чем с большинством функций, аппроксимация с помощью ряда Тейлора может помочь определить приблизительные значения для различных операций, связанных с этими функциями.

Бесполезное

Дифференцирование

Ряд Тейлора функции можно использовать для аппроксимации ее производной в конкретной точке. Члены ряда Тейлора можно дифференцировать по отдельности, тогда они примут форму

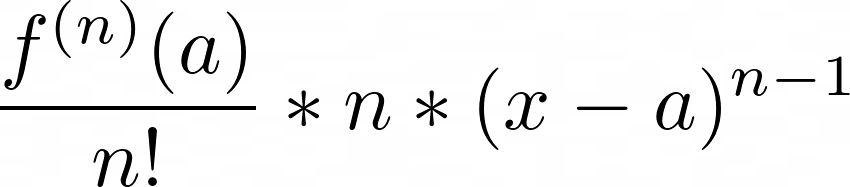
которая представляет собой просто производную степенной функции, умноженного на коэффициент ряда Тейлора. Обратите внимание, что в коде это отбросит члены, не представленные в ряде Тейлора, поскольку их коэффициенты будут равны 0.

В нашей Python-логике эти вычисления будут выполняются с помощью функции, приведенной ниже:

def approximate_derivative(self, x):
    """
        Приблизительно вычисляет производную функции f(x) по ее ряду Тейлора.
        Бесполезно, так как нам нужна производная самой функции, чтобы построить ряд Тейлора.
    """
    value = 0
    for i in range(1, len(self.coefficients)): # skip the first value (constant) as the derivative is 0
        value += self.coefficients[i] * i * ((x - self.center)**(i-1)) # differentiate each term: x^n => n*x^(n-1)
    return value

В этой функции аппроксимация производной функции находится путем перебора коэффициентов, вычисления значений производной, как описано выше, и их суммирования. Подстановка значений в эту функцию обеспечивает точную аппроксимацию производной базовой функции. Ниже приведены результаты для cos(x):

Выше приведены значения аппроксимированной функции cos(x) и ее производной (обратите внимание, что фактическая производная равна -sin(x)) в точках 0, ????/6, ????/4, ????/3, ????/2 и ????. Глядя на значения в нескольких этих точках, мы видим, что в целом получили хорошую аппроксимацию производной cos(x). Например, в точке ????/4 значение функции равно 0,707 = sqrt(2)/2, как и его производная -0,707, что является правильным значением.

К сожалению, это практически бесполезно, так как ряду Тейлора требует информация о производной функции, чтобы определить свои коэффициенты. Зачем нам нужна аппроксимация f'(x), которой требуется сама f'(x) общего вида (а значит, фактическое значение) для получения этой аппроксимации. Кроме того, существует множество различных численных методов, которые могут аппроксимировать производные без аналитического нахождения производной функции (например, методы конечных разностей), которые больше подходят для этой задачи.

Полезные

Аппроксимация значений

Одной из широко используемых целей ряда Тейлора является аппроксимация значений базовой функции. Для того, чтобы получить приблизительное значение функции, в члены ряда Тейлора подставляется x, а затем они складываются вместе. В Python-логике это выглядит следующим образом:

def approximate_value(self, x):
    """
				Аппроксимирует значение f(x) с помощью полинома Тейлора.
        x = точка аппроксимации f(x)
    """
    fx = 0
    for i in range(len(self.coefficients)):
        fx += self.coefficients[i] * ((x - self.center)**i)  # coefficient * nth term 
    return fx

Определенный интеграл

Ряд Тейлора можно использовать для аппроксимации интеграла базовой функции, поскольку члены ряда Тейлора можно интегрировать по отдельности, как мы делали это при дифференцировании. При аппроксимации интеграла члены ряда примут вид

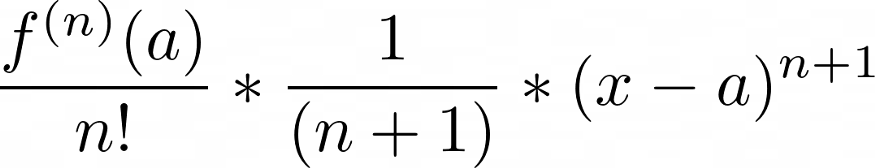
Здесь мы опять сталкиваемся со степенной функцией, но на этот раз интегрируем ее и умножаем на соответствующий коэффициент ряда Тейлора.

Однако численно мы можем рассчитать только определенный интеграл функции, так как в противном случае отсутствие значения для константы интегрирования может привести к неправильным результатам. Рассмотрим ряд Тейлора для f(x) = sin(x) с центром в 0:

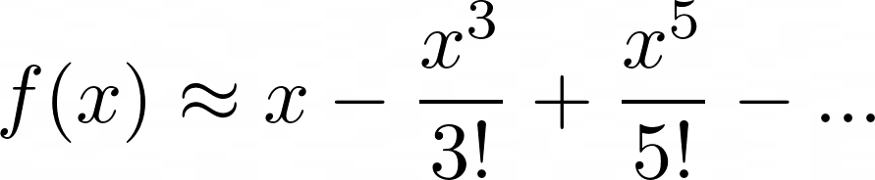
интегрирование этого полинома член за членом дает следующий полином

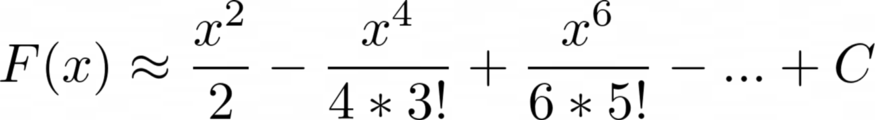
Теперь предположим, что это корректная аппроксимация интеграла sin(x) (для которой мы знаем фактический интеграл -cos(x)) и попытаемся вычислить эту функцию в 0. Значение от этого равно 0. В этом случае это можно скорректировать, установив константу интегрирования C = -1. Но нам нужно определить эту константу для каждого значения в области определения функции только для того, чтобы “исправить” интегралы, что делает бесконечное интегрирование бесполезным.

С другой стороны, определенные интегралы можно легко вычислить, интегрируя ряд Тейлора почленно и подставляя пределы интегрирования, как показано в Python-коде ниже.

def approximate_integral(self, x0, x1):
    """
        Вычисляет определенный интеграл функции, используя разложение в ряд Тейлора.
        x0 - нижний предел интегрирования
        x1 - верхний предел интегрирования 
    """

    # интегралы могут отличаться на константу, поскольку int(f(x)) = F(x) + C
    value = 0
    for i in range(len(self.coefficients)):
        value += ((self.coefficients[i] * (1/(i+1)) * ((x1 - self.center)**(i+1))) - 
                  (self.coefficients[i] * (1/(i+1)) * ((x0 - self.center)**(i+1)))) # integrate each term: x^n => (1/n+1)*x^(n+1)
    return value

Выполнение этого на нескольких значениях дает желаемые результаты для sin(x), cos (x), x³ + x², e^x и, что немного сложнее интегрировать, e^x*sin(x). В целях сокращения длины этой статьи эти результаты будут опущены. Для тех, кто сомневается, полный код будет приведен ниже. Меняйте def f(x) и проверяйте результаты самостоятельно.

Лимиты

Вместо того, чтобы показывать, как численно аппроксимировать лимиты и реализовывать это в Python, я просто приведу пример лимита, который может быть трудно определить аналитически, но его легко найти в форме ряда Тейлора.

Рассмотрим такой лимит:

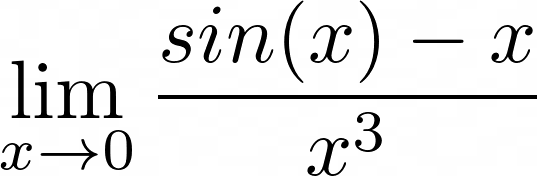
Этот лимит можно легко определить, применяя правило Лопиталя, так как он имеет форму 0/0, но давайте предположим на минуту, что мы этого не знаем (или что мы ничего не знаем о правиле Лопиталя). Как нам тогда определить этот предел? Оказывается, в этом нам может помочь ряд Тейлора, заменяющий sin(x) в пределе аппроксимацией. В этом примере будет использоваться ряд Тейлора с тремя членами:

Поскольку лимит x²/120 стремится к 0, результат равен -1/6, как и ожидалось, при оценке по правилу Лопиталя.

Заключение

Выше была представлена ​​идея ряда Тейлора, который представляет собой математический инструмент, используемый для аппроксимации любой непрерывно дифференцируемой функции полиномом, используя только информацию о производной этой функции. Была предоставлена ​​реализация на Python и обсуждены применения ряда Тейлора. Полный код с некоторыми примерами использования приведен ниже, и я советую всем, кто заинтересован в работе с этим инструментом, скопировать и потестировать этот код самим, чтобы лучше понять ряд Тейлора.

Листинг кода

usage.py

from TaylorSeries import TaylorSeries
import math

def f(x):
    return math.cos(x) #(math.e**x)*math.sin(x)*math.cos(x)

if __name__ == '__main__':
    pts = [0, math.pi/6, math.pi/4, math.pi/3, math.pi/2, math.pi]
    # pts = [-5, -4, -3, -2, -1, -0.1, 0, 0.1, 1, 2, 3, 4, 5]
    terms = 15
    center = 0
    precision = 3

    ts = TaylorSeries(f, terms, center)
    ts.print_coefficients()
    ts.print_equation()
    
    print("x\tf(x)\tApprox. f(x)\tIntegral f(x)\tDerivative f(x)")
    for x in pts:
        print("{:.3f}\t{:.3f}\t{:.3f}\t{:.3f}\t{:.3f}".format(x, f(x), ts.approximate_value(x), ts.approximate_integral(0, x), ts.approximate_derivative(x)))

TaylorSeries.py

from scipy.misc import derivative
import math

class TaylorSeries():
    def __init__(self, function, order, center=0):
        self.center = center
        self.f = function 
        self.order = order
        self.d_pts = order*2
        self.coefficients = []

       # количество точек (order) для scipy.misc.derivative
        if self.d_pts % 2 == 0: # должно быть больше, чем порядок производной, и нечетным
            self.d_pts += 1

        self.__find_coefficients()

    def __find_coefficients(self):
        for i in range(0, self.order+1):
            self.coefficients.append(round(derivative(self.f, self.center, n=i, order=self.d_pts)/math.factorial(i), 5))

    def print_equation(self):
        eqn_string = ""
        for i in range(self.order + 1):
            if self.coefficients[i] != 0:
                eqn_string += str(self.coefficients[i]) + ("(x-{})^{}".format(self.center, i) if i > 0 else "") + " + "
        eqn_string = eqn_string[:-3] if eqn_string.endswith(" + ") else eqn_string
        print(eqn_string)

    def print_coefficients(self):
        print(self.coefficients)

    def approximate_value(self, x):
        """
           Аппроксимирует значение f(x) с помощью полинома Тейлора.
       		 x = точка аппроксимации f(x)

        """
        fx = 0
        for i in range(len(self.coefficients)):
            fx += self.coefficients[i] * ((x - self.center)**i)  # coefficient * nth term 
        return fx

    def approximate_derivative(self, x):
        """
           Приблизительно вычисляет производную функции f(x) по ее ряду Тейлора.
        	 Бесполезно, так как нам нужна производная самой функции, чтобы построить ряд Тейлора.

        """
        value = 0
        for i in range(1, len(self.coefficients)): # skip the first value (constant) as the derivative is 0
            value += self.coefficients[i] * i * ((x - self.center)**(i-1)) # differentiate each term: x^n => n*x^(n-1)
        return value

    def approximate_integral(self, x0, x1):
        """
           Вычисляет определенный интеграл функции, используя разложение в ряд Тейлора.
       		 x0 - нижний предел интегрирования
   		     x1 - верхний предел интегрирования 

        """
        
        # интегралы могут отличаться на константу, поскольку int(f(x)) = F(x) + C
        value = 0
        for i in range(len(self.coefficients)):
            value += ((self.coefficients[i] * (1/(i+1)) * ((x1 - self.center)**(i+1))) - 
                      (self.coefficients[i] * (1/(i+1)) * ((x0 - self.center)**(i+1)))) # integrate each term: x^n => (1/n+1)*x^(n+1)
        return value

    def get_coefficients(self):
        """
             Возвращает коэффициенты ряда Тейлора 
        """
        return self.coefficients

Один из способов сделать вывод из статистического исследования — проверка гипотез. Это помогает нам проверить значения параметров популяции, которые угадываются на основе предварительно собранной информации. Многие области анализа данных включают в себя некоторое количество статистических испытаний, и почти всегда там используется проверка гипотез. Завтра в 16:00 в OTUS состоится открытый урок, на котором мы познакомимся с базовыми понятиями статистики и теории вероятностей, поймём, чем задачи этих областей отличаются друг от друга, концептуально рассмотрим методы проверки гипотез, и как они применяется в науке о данных на простых практических примерах. Регистрация для всех желающих — по ссылке.