В прошлой статье мы поговорили про оценку относительной производительности структуры данных или алгоритма(Big O), теперь я предлагаю взглянуть на самый популярный тип данных - Массив и оценить основные методы взаимодействия с ним.

Массив — это набор элементов одного типа, которые можно устанавливать и извлекать через непрерывный ряд целых чисел, так называемые индексы.

Эти индексы, которые в большинстве компьютерных языков начинаются с нуля, определяют, где в массиве происходит действие.

Например, чтобы получить первый элемент нашего массива, мы бы сделали get запрос с нулевым индексом. Чтобы положить во второй ячейку массива, мы бы указали индекс, равный единице. С помощью индексов мы контролируем то, что входит и выходит из нашего массива.

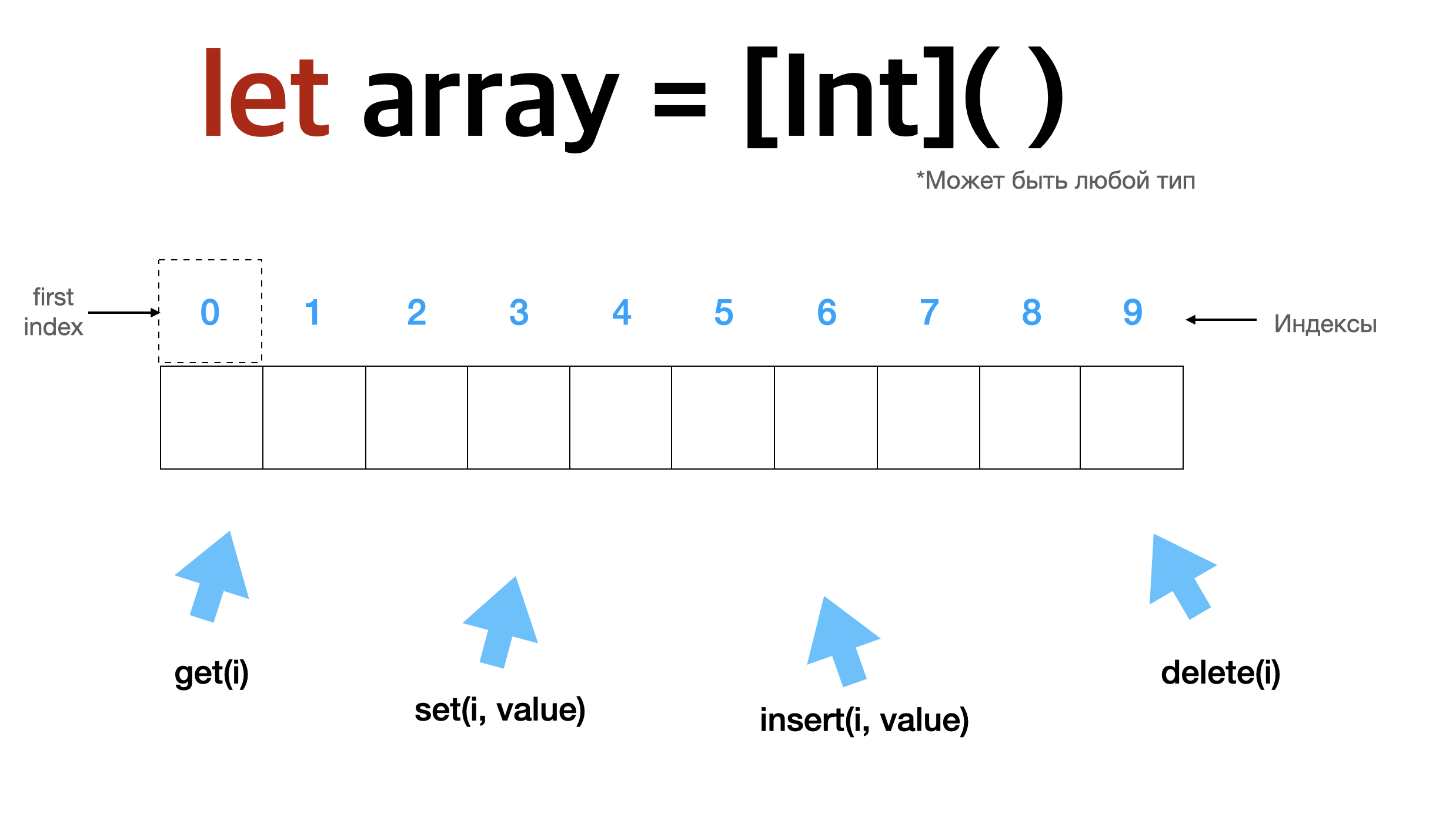
О массивах нужно знать три вещи

• Во-первых, массивы могут содержать практически все, что угодно: числа, строки, объекты и даже другие массивы.

• Во-вторых, массивы имеют фиксированный размер. Вы не видите этого в Swift, потому что в Swift, когда мы создаем множество, мы не указываем его размер. Но во многих других компьютерных языках при инициализации массива вы должны дать ему начальный размер.

• В-третьих, у массивов есть уникальная возможность случайного доступа к данным через индекс.

Связанные списки не могут этого сделать. Стеки и очереди не могу этого сделать и даже бинарные деревья поиска, а массивы могут и в этом их сила.

Теперь давайте быстро рассмотрим основные операции работы с массивом, а также взглянем на него с точки зрения относительной производительности каждой из операций, начиная с get и set.

Возможность получать и устанавливать данные в любом месте за постоянное время — вот что делает массив таким популярным.

Независимо от того, насколько большим становится массив, если вы знаете индекс нужных вам элементов, вы можете просто добраться до него внутри и получить его за O(1) постоянное время.

Именно поэтому они есть почти в каждом компьютерном языке и почему они так популярны на интервью.

Есть еще три случая работы массивов, которые нам нужно рассмотреть, чтобы понять всю их природу. И это вставка(insert), удаление(delete), а также рост массива, и его способность изменить вместимость.

Начнем со вставки.

Когда мы вставляем элемент в массив, мы на самом деле делаем три вещи. Мы копируем, вставляем и увеличиваем размер. Допустим, мы хотим вставить символ B на место под индексом один. Когда мы передаем эту инструкцию в наш массив, нам сначала нужно скопировать ее вверх. Мы должны взять элементы в первом индексе и все, что над ними, и сдвинуть их вверх на одну ячейку. Как только мы это сделали, мы освободили место в первом индексе и можем вставить B. Затем, если мы отслеживаем, насколько велики массивы, мы также можем увеличить счетчик и изменить наш размер с трех до четырех.

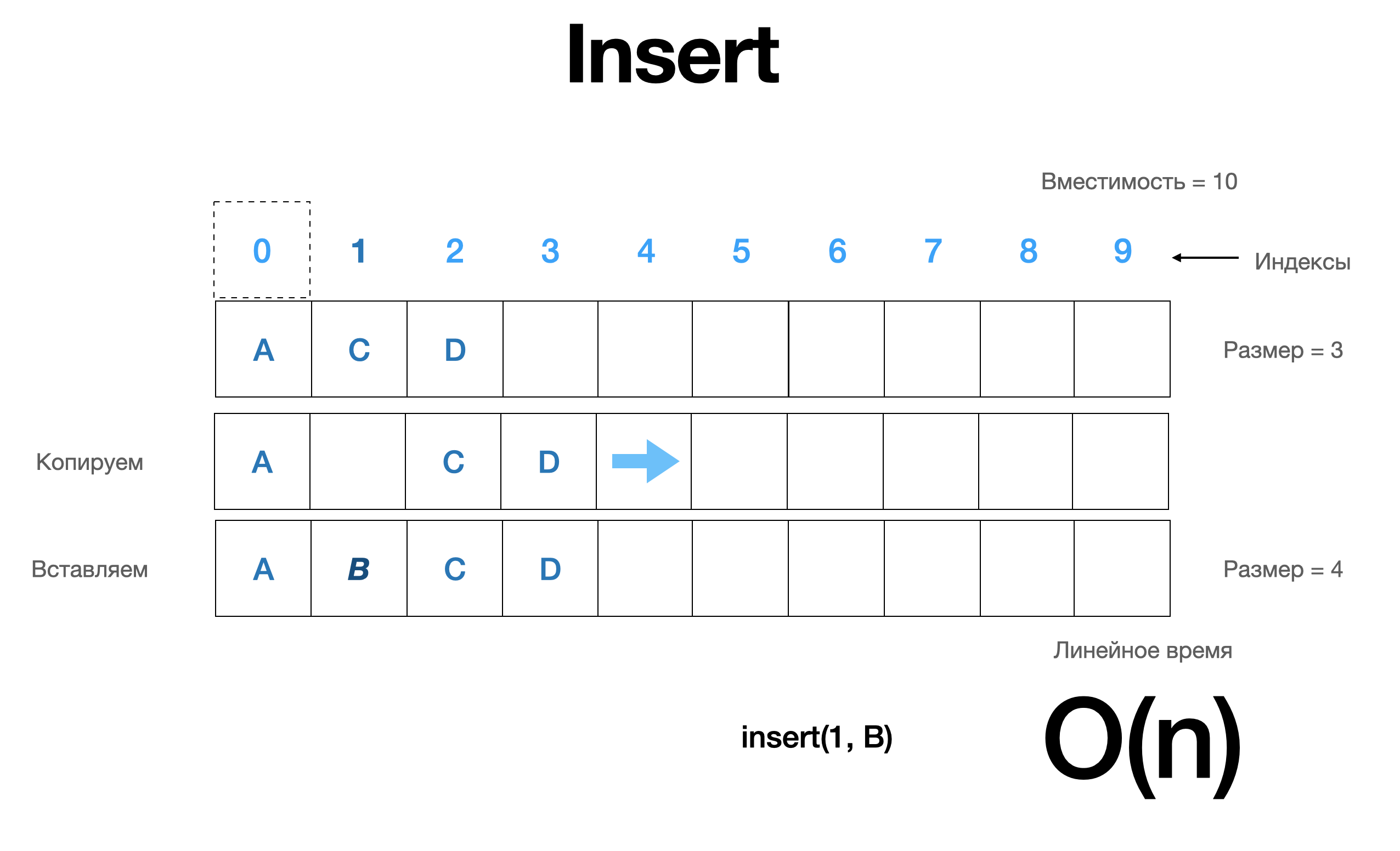
Итак заметим, что в худшем случае, там, где нам приходится перебирать, иногда почти каждый элемент в массиве, и сдвигать все вверх время операции для этого фактически является линейным или O(n).

Удаление.

Удалить — это то же самое, что и вставить, только вместо копирования вверх здесь мы копируем вниз. Допустим, мы хотим удалить тот элемент B, который мы только что вставили с индексом один.

 Здесь нам не нужно явно удалять B, мы можем просто взять все элементы выше индекса один - два, три, четыре и выше и просто сдвигайте их вниз и просто перезаписывайте все, что там было.

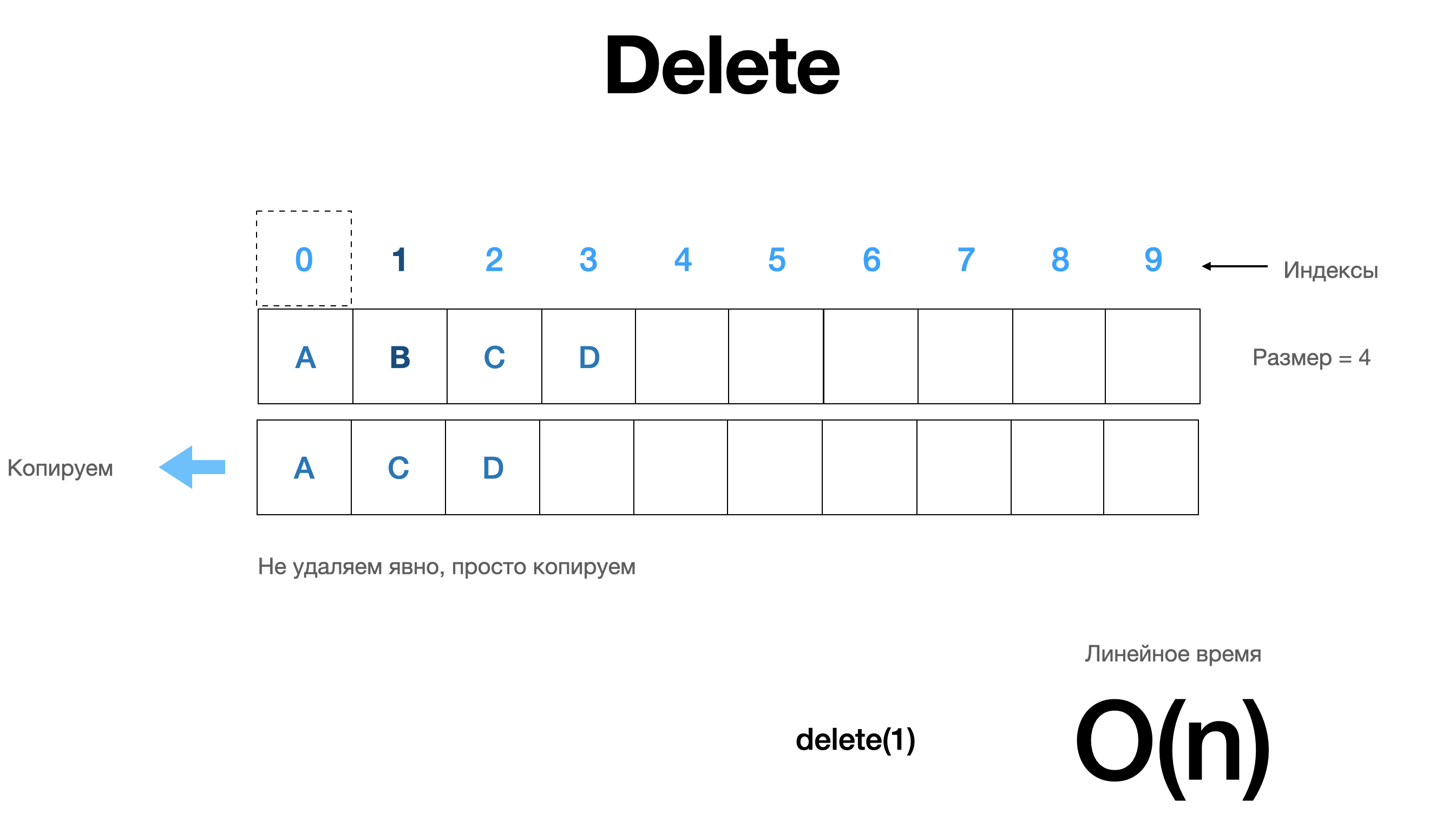
Оценка относительной производительности времени выполнения - линейная O(n), потому что в худшем случае пришлось бы сдвинуть каждый или почти элемент в массиве вниз на один, и это займет O(n) время.

Самое интересное начинается, когда наш массив просто недостаточно вместителен. Другими словами, что произойдет, если мы добавим элемент в конец нашего массива, например E, и нашему массиву, который, как мы знаем, имеет фиксированную вместительность четыре, просто некуда этот элемент положить?

В подобных ситуациях происходит удваивание размера массива.

Берем наш первоначальный массив, которого в данном случае будет четыре ячейки, создаем новый массив с размером восемь и затем мы копируем туда все существующие элементы. Переписываем A, B, C и D. Теперь, когда наш массив достаточно большой, мы можем добавить последний элемент E в самый конец под пятым индексом.

Из за изменения размера массива оценочное время O(n).

Давайте добавим E в самый конец этого массива.

Мы должны быть осторожны, потому что мы не можем просто вставить E в какую-то позицию, например, 99. Компилятор выдаст ошибку: индекс за пределами границ, потому что наш массив не достигает этого значения. Но если мы используем метод добавления(append), мы можем добавить E в конец нашего массива.

Обычное добавление элемента в массив происходит за постоянное время 0(1). Это очень, очень быстро, потому что обычно у нашего массива есть место, для нового элемента. Но в
тех редких случаях, когда нам нужно изменить вместимость массива, это будет O(n).

Рассмотрим несколько отличий массивов в Swift.

Единственное, что отличает массивы Swift, если вы пришли из других компьютерных языков, это то, что большая часть тяжелой работы, связанной с изменением размера массива, встроена прямо в сам объект массива. Если вы хотите создать массив, который может удалять, вставлять и добавлять элементы, на таком языке, как Java, или C, вам потребуется указать размер массива. В Swift все это сделано за вас. Обычно мы не указываем размер массивов. Мы просто инициализируем их, создаем, а затем используем.

Мы можем создавать массивы определенного размера, иногда такую задачу ставят на интервью, но довольно редко, поэтому вы не увидите такой код в реальном проекте.

let arrayOfSpecificSize = Array<String>(repeating: "A", count: 10)

Вывод:

1. Массив имеет фиксированный размер.

2. Рандомный доступ О(1).

3. Вставка/ удаление – О(n).

4. Массивы могут сокращаться и расти О(n).

5. Swift проделывает большую работу за нас при создании массива.

Полезные ссылки:

• Apple Developer Documentation. Swift. Array

• Статья на Хабр: "Big O нотация в Swift"

• Перемещение массива в памяти