Вы когда‑нибудь задумывались, почему результаты поиска файлов появляются так быстро? В этой статье мы рассмотрим удивительную структуру данных, известную как двоичное дерево (бинарное дерево), и узнаем, как именно она позволяет достичь такой быстрой обработки и поиска.
В этой статье вы узнаете, что такое двоичные деревья, как работает один из типов двоичных деревьев — двоичное дерево поиска, и почему сегодня они используются во многих алгоритмах.
Двои́чное де́рево — иерархическая структура данных, в которой каждый узел имеет не более двух потомков (детей). Как правило, первый называется родительским узлом, а дети называются левым и правым наследниками. Двоичное дерево является упорядоченным ориентированным деревом[1].
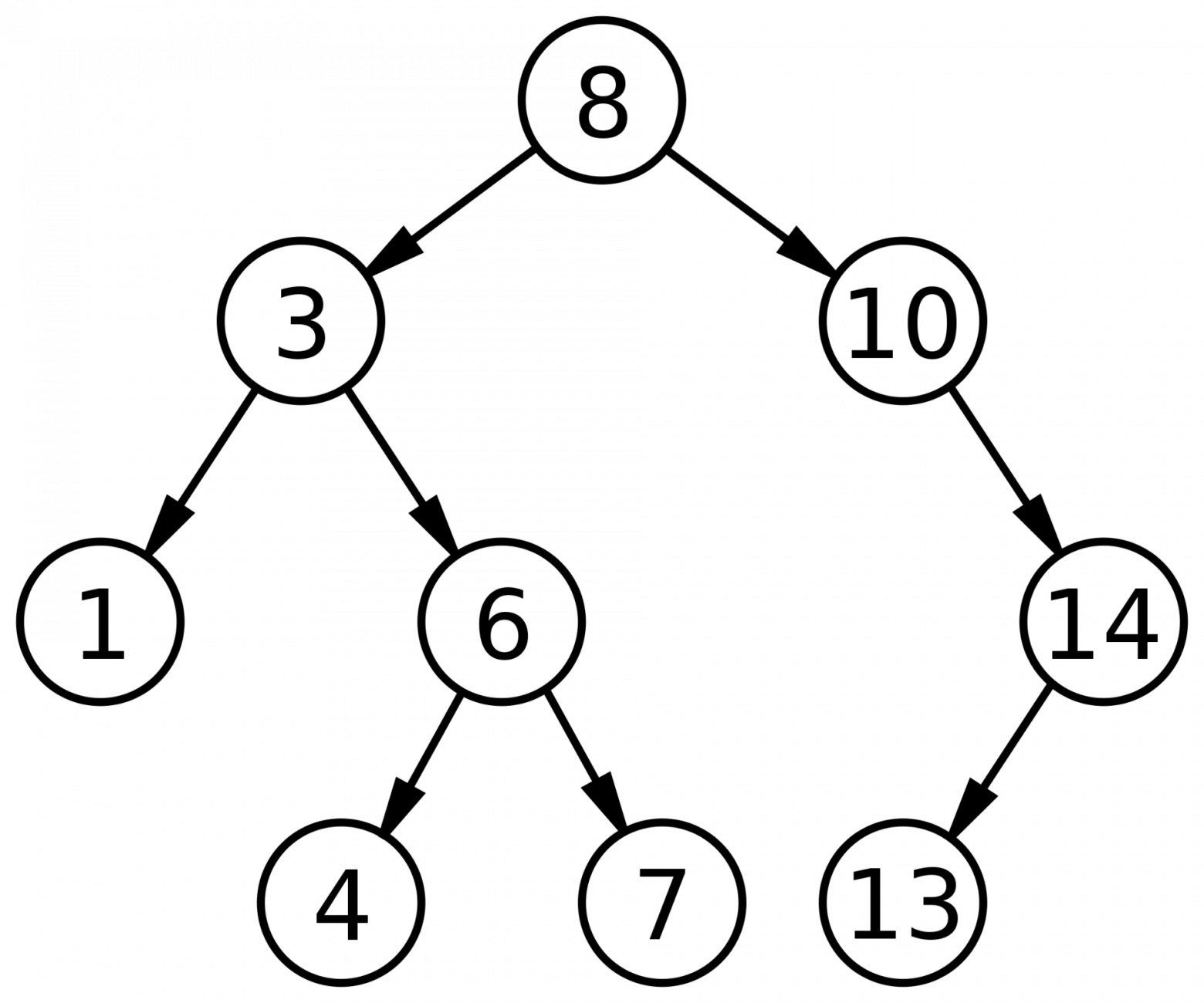
Итак, простыми словами бинарное дерево — это древовидная структура данных, в которой данные хранятся в узлах, подобно листьям на дереве. У вас есть корневой узел в верхней части. У вас есть левый и правый узлы, и в основном вы просто храните информацию в различных местах дерева, а затем просматриваете их. Иногда, когда вы тусуетесь на коктейльной вечеринке и слышите, как люди говорят о двоичных деревьях, вы слышите такие слова, как полное, идеальное и сбалансированное.
Полное бинарное дерево — это дерево, в котором каждый узел имеет ноль или два ребенка. Другими словами, не существует единичных узлов.
Примером идеального бинарного дерева может служить семейное дерево, в котором у каждого ребенка есть мать и отец.
А сбалансированное бинарное дерево — это такое дерево, которое имеет минимально возможную высоту.
Бинарные деревья, которые очень, очень глубоки, которые не сбалансированы правильно, могут быть очень неэффективными.
Поэтому мы стараемся организовать деревья минимально возможной высоты.
Еще два термина, которые вам могут встретиться, это «поиск в ширину» (Breadth‑First Search) и «поиск в глубину» (Depth‑First Search).
При проведении поиска в ширину в двоичном дереве вы обычно начинаете с корня, предполагая, что нужные вам данные находятся близко к вершине. Такой подход часто используется в алгоритмах поиска кратчайшего пути.
С другой стороны, поиск в глубину подразумевает исследование дерева до самого его конца. В этом случае вы предполагаете, что искомые данные или решение проблемы находятся глубоко в структуре дерева. Решение задач, связанных с лабиринтами, является типичным примером использования поиска в глубину в двоичном дереве.
Не стоит волноваться, если вы не знаете, как реализовать или применить эти термины на практике. Они важны для понимания, особенно в контексте технических собеседований, чтобы вы могли с уверенностью заявить: «Да, я слышал об этих терминах». Возможно, вы не сталкиваетесь с ними ежедневно в своей работе, и это нормально.
Теперь, когда мы разобрались с основной терминологией, связанной с двоичными деревьями, мы можем более глубоко погрузиться в то, как они работают на практике.
Как они работают?
Один из способов получить хорошее представление о том, как работают бинарные деревья, — это рассмотреть метод find в так называемом бинарном дереве поиска.
Бинарное дерево поиска — это дерево, узлы которого отсортированы сверху вниз. Отсортированные узлы означают, что все узлы слева от родителя меньше родителя. В то время как все узлы справа больше родительского. Под больше или меньше мы понимаем ключи. Используемые ключи уникально представляют этот узел. Сортируя двоичное дерево сверху вниз, мы теперь имеем дерево в таком состоянии, что можем сделать с ним что‑то очень мощное и крутое — Мы можем начать быстрый поиск.
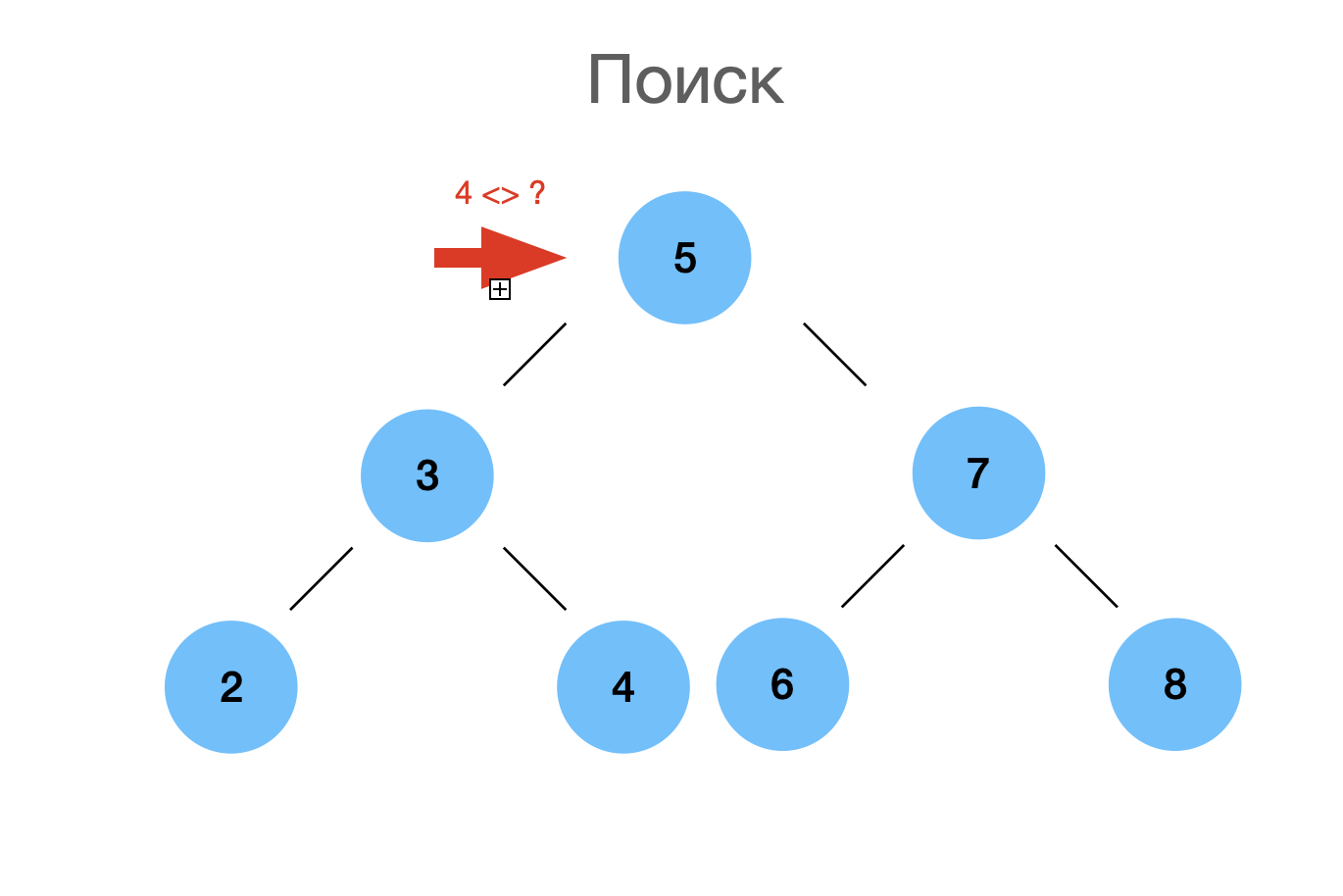
Подробное описание
Реализация find для двоичного дерева поиска выглядит примерно так. Допустим, мы ищем число четыре или ключ четыре в нашем упорядоченном двоичном дереве. Мы начинаем с корня, с самой вершины. Мы спрашиваем, тот ли это ключ, который мы ищем? Если это не так, мы продолжаем поиск и спрашиваем: ну, а искомый ключ меньше или больше текущего узла? В данном случае, поскольку четыре меньше пяти, мы идем влево и здесь повторяем вопрос. Есть ли у нас четверка? Если нет, продолжаем искать. Четыре меньше, чем три? В данном случае четыре больше трех. Поэтому мы идем вправо и продолжаем этот процесс, продвигаясь все дальше и дальше по двоичному дереву, пока не найдем либо искомый узел, либо не достигнем конца нашего дерева, в этом случае мы просто вернем null.
Двоичные деревья состоят из более мелких деревьев и поддеревьев, которые вложены друг в друга. Когда мы рассматриваем их код, мы видим, что это становится очевидным благодаря рекурсии. Кроме того, важно отметить, что при поиске или принятии решений в двоичном дереве мы сокращаем область поиска вдвое каждый раз. Каждый переход от одного уровня к следующему через узел фактически устраняет половину дерева. Это особенность двоичных деревьев, которая позволяет выполнять поиск очень быстро со временной сложностью O(log n). Этот непрерывный процесс сокращения вдвое обеспечивает временную сложность O(log n) для поиска в двоичных деревьях. Чтобы увидеть и понять, как это работает, давайте рассмотрим его в коде.
class Node {
var key: Int = 0
var left: Node?
var right: Node?
init(_ key: Int) {
self.key = key
}
var min: Node {
if left == nil {
return self
} else {
return left!.min
}
}
}
class BST {
var root: Node?
// вставка
func insert(key: Int) {
root = insertItem(root, key)
}
private func insertItem(_ node: Node?, _ key: Int) -> Node {
// Если узел равен nil - значит сюда мы и вставим
guard let node = node else {
let node = Node(key)
return node
}
if key < node.key {
node.left = insertItem(node.left, key)
}
if key > node.key {
node.right = insertItem(node.right, key)
}
// Если мы дошли сюда значит у нас дубликат.
// Дубликаты запрещены в дереве поэтому просто игнорируем
// Мы закончили, Наше дерево готово!
return node;
}
// поиск
func find(key: Int) -> Int? {
guard let root = root else { return nil }
guard let node = find(root, key) else { return nil }
return node.key
}
private func find(_ node: Node?, _ key: Int) -> Node? {
guard let node = node else { return nil }
if node.key == key {
return node
} else if key < node.key {
return find(node.left, key)
} else if key > node.key {
return find(node.right, key)
}
return nil
// Note: дублирование ключей запрещено так что нам не нужна проверка
}Описание кода
Класс Node: Этот класс представляет узел дерева. Каждый узел имеет ключ (key), который является значением узла, а также ссылки на левого и правого потомка (left и right). У него есть инициализатор, который принимает ключ в качестве входного параметра, и свойство min, которое возвращает узел с наименьшим ключом в поддереве.
Класс BST (Binary Search Tree): Этот класс представляет собой двоичное дерево поиска. У него есть корневой узел (root) и две основные функции:
Функция insert(key: Int): Это функция добавляет новый узел с указанным ключом в дерево. Она вызывает вспомогательную функцию insertItem, которая рекурсивно ищет место для вставки нового узла и создает его при достижении nil (то есть достигнута конечная точка в ветке дерева). Если в дереве уже присутствует узел с таким же ключом, то новый узел не будет добавлен, поскольку дубликаты запрещены.
Функция find(key: Int): Эта функция ищет узел с заданным ключом в дереве. Она также использует вспомогательную функцию find, которая рекурсивно ищет узел в дереве. Если узел с заданным ключом не найден, функция возвращает nil.
Вставка(insert)
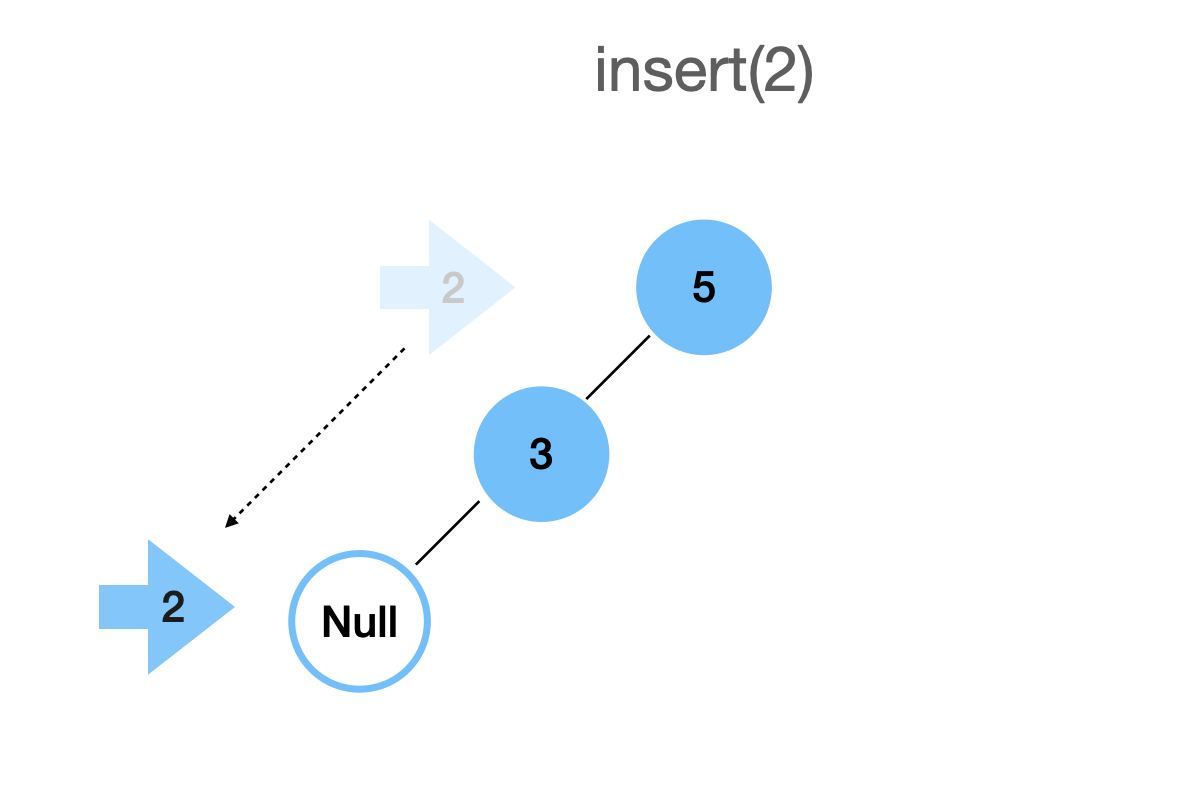
Вставка в двоичное дерево поиска — это процесс, который требует точности и внимания к деталям, чтобы сохранить важный порядок узлов. Давайте представим, что у нас есть задача вставить число два в наше дерево.
Вот как мы бы это сделали:
Мы начнем наш путь с вершины дерева, где сейчас находится число пять. Задумаемся на мгновение: мы собираемся вставить двойку, так что нам нужно определить, куда она будет подходить лучше всего. Вспомним правило двоичного дерева: все числа меньше родительского узла должны быть слева. В нашем случае двойка меньше пяти, поэтому мы уверенно направляемся к левой ветке дерева, где находится тройка. Теперь у нас новый узел для сравнения — это тройка. Проверяем ещё раз: наше число, двойка, меньше тройки, так что мы продолжаем движение вниз по левой ветке. Наша цель — найти место, которое ещё не занято, или, говоря техническим языком, достичь nil значения в нашем дереве. В этом месте мы и вставим нашу двойку.
Нахождение минимума(findMin)

Теперь, прежде чем мы перейдем к работе с удалениями, один метод, который действительно полезно разобрать, — это поиск минимума в дереве двоичного поиска. И это на самом деле очень просто.
Если вы просто вспомните, что всякий раз, когда мы смотрим на дерево двоичного поиска, мы знаем, что все элементы слева будут меньше, чем все элементы справа.
Поэтому все, что нам действительно нужно сделать, это пройти по левой стороне нашего дерева, пока мы не встретим ноль.
И когда мы это делаем, это означает, что нет элементов меньше, чем тот, на котором мы сейчас находимся, поэтому мы можем просто вернуть этот узел.
В коде это будет выглядеть примерно так.
func findMin() -> Int {
guard let root = root else { return 0 }
return findMin(root).key;
}
private func findMin(_ node: Node) -> Node {
return node.min;
}Мы можем поместить эту ответственность прямо в сам класс узла, и это всего лишь четыре строчки кода. Когда мы вызываем minimum на узле, мы просто проверяем, есть ли что‑нибудь слева от нас? Если нет, мы знаем, что достигли минимума, и можем просто вернуть его. Но если нет, давайте просто продолжим повторять и идти вниз по левой стороне дерева, пока не встретим этот null, а затем вернем его.
Обработка удалений
Удаление элементов из двоичного дерева поиска — это вполне достижимая задача, хотя и с некоторыми нюансами. Как вы упомянули, у нас есть три различных случая для рассмотрения: узлы без детей, узлы с одним ребенком и узлы с двумя детьми.
Узел без детей — это самый простой случай. Здесь наш узел — это лист дерева, он сам по себе, без каких‑либо ветвей, растущих от него. Чтобы удалить такой узел, достаточно просто оборвать связь, которая связывает его с родителем. Можно представить, что этот узел — это капля воды на листе дерева, которая просто катится и падает, когда мы ее трогаем.
Узел с одним ребенком — это немного сложнее, но всё же вполне управляемый случай. Здесь у нашего узла есть одна ветка — может быть либо слева, либо справа. Чтобы удалить этот узел, мы просто перенаправляем ссылку от родительского узла к ребенку этого узла. Это как переключить стрелку дорожного указателя, чтобы она указывала прямо на следующий узел.
-
Наконец, узел с двумя детьми — это наиболее сложный случай. Однако, несмотря на это, в нём есть своя логика и порядок. Здесь наш узел имеет две ветви, и мы не можем просто перенаправить ссылку, как в предыдущем случае. Вместо этого мы находим минимальный узел в правом поддереве (или максимальный узел в левом поддереве), заменяем удаляемый узел этим узлом и затем удаляем найденный узел.
Рассмотрим код:
func delete(key: Int) {
guard let _ = root else { return }
root = delete(&root, key);
}
private func delete(_ node: inout Node?, _ key: Int) -> Node? {
guard let nd = node else { return nil }
if key < nd.key {
nd.left = delete(&nd.left, key)
} else if key > nd.key {
nd.right = delete(&nd.right, key)
} else {
// Кейс 1: Нет детей
if nd.left == nil && nd.right == nil {
return nil
}
// Кейс 2: Один ребенок
else if nd.left == nil {
return nd.right
else if nd.right == nil {
return nd.left
}
// Кейс 3: Двое детей
else {
// Находим минимальный узел справа
// (также может быть максимум слева)
let minRight = findMin(nd.right!)
// копируем значения
nd.key = minRight.key
// удаляем ноду которую только что копировали
nd.right = delete(&nd.right, nd.key)
}
}
return nd
}Обход двоичного дерева
Ранее мы рассмотрели два различных способа обхода двоичного дерева. Вы можете пройтись по двоичному дереву в ширину и в глубину. В этом разделе мы рассмотрим три различных способа, которыми можно пройтись по двоичному дереву в глубину, и несколько различных способов обхода.
Обход двоичного дерева — это процесс посещения каждого узла в дереве в определенном порядке. Существуют три основные стратегии обхода: «inorder» (симметричный обход), «preorder» (прямой обход) и «postorder» (обратный обход). Каждый из этих методов обхода применяется для различных задач и имеет свои особенности.
Inorder (Симметричный обход): При этом типе обхода, мы сначала посещаем левый дочерний узел, затем родительский узел, и наконец правый дочерний узел. Если используется на дереве двоичного поиска, симметричный обход выводит узлы в возрастающем порядке.
Preorder (Прямой обход): В этом типе обхода сначала посещается родительский узел, затем его левый дочерний узел, и наконец правый дочерний узел. Этот метод обхода полезен для создания копии дерева, так как он клонирует корень дерева перед его поддеревьями.
Postorder (Обратный обход): Здесь сначала посещаются оба дочерних узла, и только после этого посещается родительский узел. Этот метод обхода полезен при удалении узлов дерева, так как он сначала удаляет дочерние узлы, прежде чем удалять родительский узел.
Важно помнить, что во всех этих методах обхода каждый узел посещается ровно один раз.
Характеристики времени выполнения
Когда мы говорим о двоичных деревьях поиска, одно из самых важных понятий — это временная сложность, которая обозначается как O(log n). Это относится к скорости, с которой происходят операции поиска, вставки и удаления в двоичном дереве поиска.
Если вы пытаетесь понять, что означает O(log n), подумайте о том, как работает двоичное дерево. Каждый раз, когда мы проходим через уровень дерева, количество операций, которые нам нужно выполнить, уменьшается вдвое. То есть, мы «расщепляем» пространство поиска на половины с каждым шагом. Это и есть логарифмическое сокращение, отсюда и выражение log n. Так что просто запомните: время, которое потребуется для выполнения операций поиска, вставки или удаления в двоичном дереве поиска, определяется как O(log n).

Заключение
Отлично, вы теперь обладаете пониманием двоичных деревьев поиска, что будет невероятно полезно на собеседованиях. Важно помнить, что основные принципы двоичного дерева поиска — это упорядоченность и рекурсия. Рекурсия является ключевым аспектом здесь, так как она постоянно применяется.
Вы уже ознакомились с некоторыми ключевыми терминами, такими как полные, совершенные и сбалансированные двоичные деревья, и вы понимаете, что внешний вид двоичного дерева может варьироваться в зависимости от того, насколько оно заполнено.
Вы также усвоили, что существуют разные подходы к исследованию дерева: можно идти вглубь или вширь. Если вы услышите эти термины, вы будете знать, о чем идет речь. И помимо глубины, есть различные способы обхода двоичного дерева.
Но самое главное, что стоит помнить о двоичных деревьях поиска, — это их эффективность в вопросах поиска. Их «суперсила» — это возможность осуществлять поиск со скоростью O(log n), что означает очень быстрый поиск.
Спасибо, что дочитали до конца! Удачи в ваших проектах и дальнейшем развитии в области iOS‑разработки! Подписывайтесь на мой канал с авторским контентом SwiftyGroup.


wataru
Вам стоит дать определение "двоичного дерева поиска" в самом начале. Потому что все ваши следующие определения, вроде сбалансированности, хоть и технически применимы ко всем деревьям, на практике используются только в деревьях поиска. Потому что именно упорядоченность ключей позволяет делать всякие операции за один спуск по дереву, из-за чего высота дерева начинает играть роль.
Далее, временная сложность O(log n) получается только у сбалансированных деревьев. Ибо это свойство гарантирует примерно уменьшение дерева в 2 раза на каждой развилке.
Ваши операции добавления/удаления не балансируют дерево, поэтому вся ваша структура работает за O(n) в худшем случае. Если я вызову операцию добавления с увеличивающимеся числами, то вы пострите "палку", где у всех вершин нет левого ребенка, но почти у всех есть только правый ребенок.
Балансированные деревья поиска немного более сложные структуры данных, вроде AVL-, красно-черных- или декартовых деревьев.
Dinozavr2005 Автор
привет, спасибо за Ваш комментарий, согласен с замечаниями по определению и по временной сложности, в ближайшее время добавлю информацию в статью.