Что нужно знать начинающему разработчику на собеседовании

Каков наиболее эффективный способ отсортировать миллион 32-битных пользователей Это частый вопрос на собеседовании в таких компаниях как Google. Чтобы ответить на него нам нужно применить алгоритм сортировки. Сегодня мы разберем три основные вида сортировок = Bubble sort (пузырьковая сортировка), Merge sort (сортировка слиянием) и Quick sort (быстрая сортировка). Благодаря этим знаниям мы легко сможем справится с вопросами и задачами по этой теме на интервью

Давайте начнем с самого простого из них - Bubble sort

Пузырьковая сортировка — это своего рода аккуратный алгоритм сортировки, потому что на самом деле он находит наибольшее число в массиве за несколько проходов и поднимает его в конец (заставляет его всплывать в пузыре).

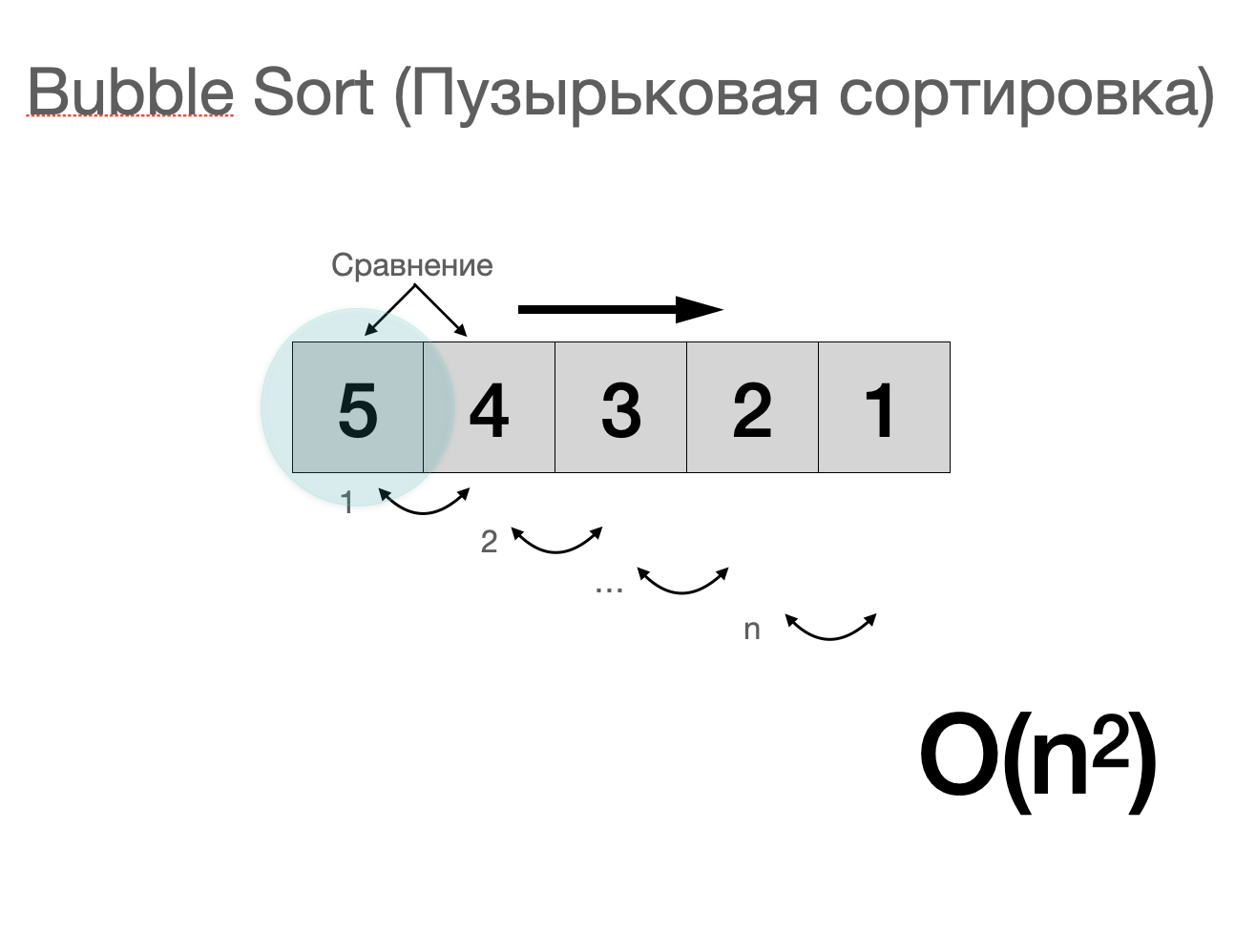
Взгляните на картинку с примером. Дан не отсортированный массив с цифрами в обратном порядке (5,4,3,2,1). Давайте попробуем его отсортировать, чтобы цифры были по порядку (1,2,3,4,5), применим наш алгоритм и посмотрим, как он здесь работает.

Далее посмотрим, как это выглядит в коде

class BubbleSort {
    func sort(_ array: [Int]) -> [Int] {
        var arr = array
        let n = arr.count
        for i in 0..<n-1 {
            for j in 0..<n-i-1 {
                if arr[j] > arr[j+1] {
                    // меняем местами
                    let temp = arr[j]
                    arr[j] = arr[j+1]
                    arr[j+1] = temp
                }
            }
        }
        
        return arr
    }
}

let bubbleSort = BubbleSort()
bubbleSort.sort([5, 4, 3, 2, 1])

Пузырьковая сортировка в коде, это два цикла for. У нас есть цикл for, который начинается с начала массива и фиксирует наш проход по нему. Затем у нас есть еще один указатель на J, который мы используем для сравнения двух последовательных чисел между собой. И если одно число больше другого, меняем местами. При замене мы временно копируем значения в переменные.

 У нас получилось два вложенных цикла for - один внутри другого, а это значит, что оценка скорости алгоритма будет - O(n²).

Более быстрая сортировка это - Merge sort

Сортировка слиянием — это алгоритм «разделяй и властвуй», и он работает благодаря шагу слияния. На этом шаге нам просто нужно объединить два массива в один. Именно он на самом деле является сутью алгоритма. Давайте сначала изучим его, а затем посмотрим на остальную часть алгоритма.

Мы разобрали основной шаг алгоритма слияние, но прежде, чем выполнить его, сначала нужно взять этот массив и разбить его в определенный формат.

 Давайте посмотрим, как теперь сортировка слиянием разбивает массив. Первый шаг алгоритма: разбитие массива на мелкие части одинакового размера , поэтому он берет каждый элемент этого массива и создает массив с этим элементом, в основном путем непрерывного деления на два, пока он не сократит его до наименьших элементов (отдельных чисел) в массиве.

Первый шаг, это фаза разделения. Затем мы только что рассмотрели вторую фазу, где берутся мельчайшие элементы или те отдельные элементов массива и непрерывно комбинирует их, используя этот алгоритм сортировки слиянием.И причина, по которой сортировка слиянием работает, конечно же, в том, что эти массивы постоянно отсортированы.

Один из простых способов запомнить характеристики сортировки слиянием во время выполнения — визуализировать то, что на самом деле происходит, когда мы запускаем алгоритм. Помните, когда мы запускаем этот алгоритм, мы постоянно рекурсивно делим массив на множество частей. Всякий раз, когда вы имеете рекурсивное деление пополам, знайте это – log n. Затем вторая часть алгоритма заключалась в том, что мы должны объединять их n количество раз. Поэтому, когда вы объединяете (log n) с n, получаем основное время выполнение сортировки слиянием - O (n log n).

И наконец - Quick Sort

Быстрая сортировка — действительно аккуратный алгоритм, также он очень короткий: запомнив основные моменты, его легко написать «из головы»

У алгоритма всего три шага:

1. Выбрать элемент из массива. Назовём его опорным(pivot).

2. Разбиение: перераспределение элементов в массиве таким образом, что элементы, меньшие опорного, помещаются перед ним, а большие или равные - после.

3. Рекурсивно применить первые два шага к двум подмассивам слева и справа от опорного элемента. Рекурсия не применяется к массиву, в котором только один элемент или отсутствуют элементы.

Простым языком:  вы выбираете что-то, называемое pivot, в любом месте вашего массива, лучше где-то в середине и  вращаем числа вокруг этой опорной точки. После того, как мы проделаем это несколько раз, у нас останется два отсортированных массива из нашего основного.  Все числа слева меньше, чем у опорной точки, а все числа справа больше. Может быть, вы видите, к чему все идет, потому что теперь мы можем просто снова применить тот же алгоритм, только к этим двум отдельным массивам, и повторить процесс. И мы просто продолжаем делать это и делать это, пока все числа в алгоритме не будут отсортированы.    

Давайте посмотрим на пример.

Взглянем как это выглядит в коде:

func quicksort<T: Comparable>(_ a: [T]) -> [T] {
  guard a.count > 1 else { return a }
 
  let pivot = a[a.count/2]
  let less = a.filter { $0 < pivot }
  let equal = a.filter { $0 == pivot }
  let greater = a.filter { $0 > pivot }
 
  return quicksort(less) + equal + quicksort(greater)
}

let list = [ 10, 0, 3, 9, 2, 14, 8, 27, 1, 5, 8, -1, 26 ]
quicksort(list)

Еще больше примеров тут

Время выполнения для быстрой сортировки равно O(n log n), как и для сортировки слиянием, но это более быстрый алгоритм, чем сортировка слиянием. Это самый быстрый из трех. Пусть это будет ключевой вывод в этой статье. Пузырьковая сортировка самая медленная, сортировка слиянием вторая и первое место - быстрая сортировка.

И если у вас возникли проблемы с запоминанием времени выполнения быстрой сортировки, просто помните, что мы постоянно уменьшаем вдвое это, что даст нам нашу характеристику log 2 n. Мы делаем это n раз. Вот почему это операция O (n log n).

Вот и все, друзья, вы только что покорили и только что прошлись по всем основным алгоритмам сортировки.