Всем привет! Меня зовут Пантелеев Александр и я бэкенд-разработчик в компании Bimeister.

Постараюсь описать исчерпывающе, кратко и понятно суть основных паттернов хранения деревьев в реляционных базах данных. Надеюсь, что статья будет полезна тем, кто до сего момента не сталкивался с такими паттернами, и станет отправной точкой в их понимании.
В этой статье не будет терминов реляционной алгебры или базы данных: таких как атрибут, домен и т. д. Также не будет привязки к какой-либо СУБД, какому-либо SQL или пользовательскому коду.
Всего существует 4 общепринятых паттерна хранения деревьев:
Adjacency List;
Nested Sets;
Closure Table;
Materialized Path.
Кратко рассмотрим каждый из них.
Adjacency List
Описание
Это самый простой и интуитивный вариант хранения. Каждому элементу сопоставляется его свойство — его родительский элемент. Если родительский элемент не задан, то он считается корневым элементом.
Когда связь сопоставления элемента и родительского элемента хранится отдельно от элемента, Adjacency List можно рассматривать как частный случай Closure Table со связями 1 уровня.
Преимущества
Лёгкость реализации, а также простота вставки, удаления и перемещения элементов в дереве.
Недостатки
Можно получить только непосредственные дочерние элементы. Чтобы получить все дочерние элементы, необходимо выполнить рекурсивный запрос либо производить множественные запросы.
Примеры

Элемент |
Родительский элемент |
A |
- |
B |
A |
C |
B |
D |
C |
E |
B |
F |
B |
G |
A |
H |
G |
I |
A |
Рассмотрим элемент «B»:
Чтобы получить все его дочерние элементы, нам необходимо выбрать элементы, удовлетворяющие условию:
Родительский элемент равен «B»
Nested Sets
Описание
Каждому элементу сопоставляются свойства: левый и правый индекс, на основе которых будет производиться выборка дочерних элементов. Также, но необязательно, элемент может дополняться свойством уровень для указания желаемого уровня вложенности выбираемого элемента относительно корня или родительского элемента.
Запрос получения дочерних элементов строится на том факте, что для любого дочернего элемента выполняются условия:
левый индекс больше левого индекса родительского элемента;
правый индекс меньше правого индекса родительского элемента.
При создании и обновлении дерева левые и правые индексы элементов дерева, при его обходе в глубину, заполняются по определённым правилам.
Преимущества
Возможность получения дочерних элементов любых уровней вложенности с помощью простого одиночного запроса.
Недостатки
При использовании целочисленных типов для левого и правого индекса и уровня необходимо пересчитывать индексы всех связанных элементов в следующих случаях:
при вставке элементов;
при удалении элементов;
при изменении родительского элемента.
Пример
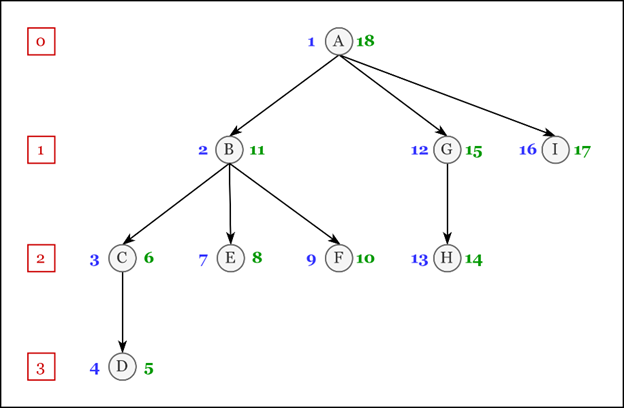
Элемент |
Левый индекс |
Правый индекс |
Уровень |
A |
1 |
18 |
0 |
B |
2 |
11 |
1 |
C |
3 |
6 |
2 |
D |
4 |
5 |
3 |
E |
7 |
8 |
2 |
F |
9 |
10 |
2 |
G |
12 |
15 |
1 |
H |
13 |
14 |
2 |
I |
16 |
17 |
1 |
Рассмотрим элемент «B». Его значения свойств:
левый индекс = 2;
правый индекс = 11;
уровень = 1.
Чтобы получить все его дочерние элементы, нам необходимо выбрать элементы, удовлетворяющие условию:
левый индекс больше 2 И правый индекс меньше 11
Чтобы получить его непосредственные дочерние элементы, нам необходимо добавить к условию ограничение на уровень:
левый индекс больше 2 И правый индекс меньше 11 И уровень = 1
Чтобы получить дочерние элементы вместе с родительским элементом, нам необходимо ослабить условия индексов:
левый индекс больше или равен 2 И правый индекс меньше или равен 11
Closure Table
Описание
Суть этого паттерна заключается в том, что мы сопоставляем каждому элементу множество связей со всеми его дочерними элементами или сопоставляем каждому элементу множество связей со всеми его родительскими элементами. Также, но необязательно, связь может содержать свойство Уровень. Уровень задаёт расстояние между элементами в дереве.
Если в запросе получения дочерних или родительских элементов по элементу необходимо получать в результате сам элемент, то нужно добавлять связь элемента самого на себя — то есть со значением уровня связи 0.
Преимущества
Возможность получения дочерних элементов любых уровней вложенности с помощью простого одиночного запроса.
Возможность получения родительских элементов любых уровней с их иерархией относительно дочернего элемента с помощью простого одиночного запроса.
Недостатки
При вставке и удалении элементов из дерева, а также при перемещении элементов в дереве необходимо пересчитывать все связи, в которых этот элемент участвует.
Пример
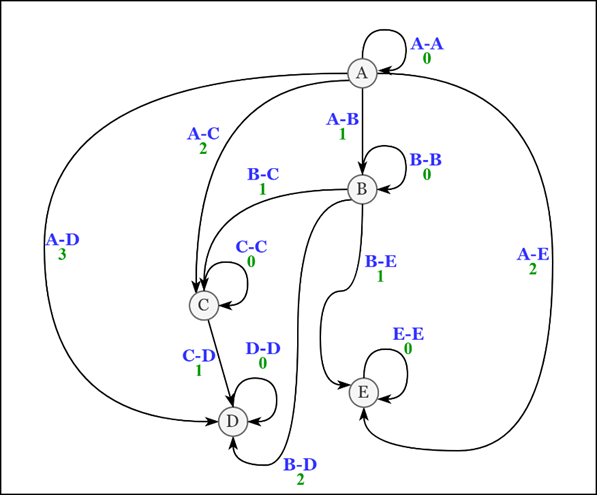
Родительский элемент |
Дочерний элемент |
Уровень |
A |
A |
0 |
A |
B |
1 |
A |
C |
2 |
A |
E |
2 |
A |
D |
3 |
B |
B |
0 |
B |
C |
1 |
B |
E |
1 |
B |
D |
2 |
C |
C |
0 |
C |
D |
1 |
E |
E |
0 |
D |
D |
0 |
Рассмотрим элемент «B»:
Чтобы получить все его дочерние элементы, нам необходимо выбрать элементы, удовлетворяющие условию:
родительский элемент равен «B»
Чтобы получить его непосредственные дочерние элементы, нам необходимо добавить к условию ограничение на уровень:
родительский элемент равен «B» И уровень = 1
Чтобы получить дочерние элементы вместе с родительскими, нам необходимо ослабить условия индексов:
родительский элемент равен «B» И уровень = 0
Чтобы получить все его родительские элементы, нам необходимо выбрать элементы, удовлетворяющие условию:
дочерний элемент равен «B»
Materialized Path
Описание
Каждому элементу сопоставляется свойство — его путь, который является последовательностью родительских элементов заданного элемента, отсортированных по уровням. В общем случае, чтобы формировать гибкие запросы, тип реализации свойства путь должен поддерживать сопоставление по шаблону в каком-либо виде. При денормализации пути в отдельную таблицу получается разновидность Closue Table.
Условия запросов на получение элементов заключается в применении предиката над свойством путь.
Преимущества
Возможность получения дочерних элементов любых уровней вложенности.
Возможность получения родительских элементов любых уровней с их иерархией относительно дочернего элемента.
Лёгкость вставки элемента.
Лёгкость удаления элемента.
Недостатки
Сложность изменения родителя для существующего элемента. Для всех дочерних элементов необходимо пересчитать новый путь.
Операции со свойством путь обычно происходят долго.
Пример
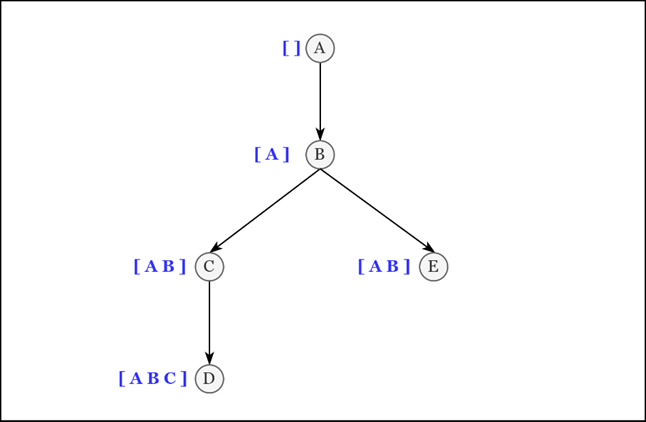
Элемент |
Путь |
A |
|
B |
A |
C |
A B |
D |
A B C |
E |
A B |
Рассмотрим элемент «B»:
Чтобы получить все его дочерние элементы, нам необходимо выбрать элементы, удовлетворяющие условию:
путь содержит «B»
Чтобы получить его непосредственные дочерние элементы, нужно указать позицию, в которой содержится элемент. В примере путь отсортирован так, что последняя часть пути — это непосредственный родительский элемент:
последняя часть пути равна «B»
Заключение
Мы кратко рассмотрели основные паттерны хранения деревьев в реляционной базе данных. Их основные достоинства и недоставки, а также на примерах рассмотрели основные запросы к ним. В этой статье не были рассмотрены алгоритмы построения и заполнения метаданных деревьев, то есть операции добавления, обновления и удаления элементов.
Комментарии (15)

ChuckLaud
24.06.2022 09:30-3Увы, пост небрежно оформлен. Лучше исправить, иначе, как мне кажется, минусы неизбежны.

bid
24.06.2022 11:06+4Nested Sets
…
левый индекс меньше 2 И правый индекс больше 11 …
левый индекс меньше или равен 2 И правый индекс больше или равен 11Должно быть наоборот:
левый индекс > 2 И правый индекс < 11 левый индекс ≥ 2 И правый индекс ≤ 11

Akina
24.06.2022 11:32+1Materialized Path на самом деле существует в двух вариантах. Первый описан - храним имя и путь. Второй же даже не упомянут. Храним только имя, но в виде полного характеристического, т.е. с полным путём от корня. Достоинства и недостатки те же.
И ещё. Вы упустили один недостаток (хотя это, возможно, и выходит за рамки статьи). А именно трудность выявления ошибок - точнее, факта наличия циклов для Adjacency List и невалидных путей (ссылка на несуществующий узел) для Materialized Path. И если вторая проблема при правильной работе с данными может быть только последствием какого-то сбоя, который сам по себе есть основание для валидации, то вот факт образования цикла при штатном изменении данных никак себя не проявляет. Для остальных методов хранения выявление ошибок проще (вернее, выше вероятность выявления факта наличия ошибки и необходимости валидации и санации при очередной операции с данными), особенно если узел хранит уровень.

0x1000000
24.06.2022 11:35Забавно, в свое время самостоятельно дошел до идеи «Closure Table», а это оказывается уже известный паттерн )
Могу лишь добавить, что если данных в основной таблице с деревом не очень много, а возиться с обновлением «Closure Table» не охота, то в принципе, можно обойтись и «view» c рекурсивной CTE, позже заменив её на реальную таблицу (в случае проблем с производительностью).Пример CTE;WITH CTE_Recursive AS ( SELECT Id, ParentId FROM dbo.TreeData UNION ALL SELECT [PREVIOUS].Id, [CURRENT].ParentId FROM dbo.TreeData [CURRENT] INNER JOIN CTE_Recursive [PREVIOUS] ON [PREVIOUS].ParentId = [CURRENT].Id ) ,CTE_TreeRelation AS ( SELECT Id, ParentId FROM CTE_Recursive UNION ALL SELECT Id, Id as ParentId FROM dbo.TreeData ) SELECT * FROM CTE_TreeRelation

Shreedeer
24.06.2022 12:46+1Недавно делал тестовое и интуитивно дошёл до Adjacency List, интересно было почитать о других вариантах, хотелось бы ещё примеров из реальной жизни с разными методами хранения.

sepetov
24.06.2022 13:59+2Конкретно я использовал древовидное хранение в складском хозяйстве. На складе используется адресное хранение, ну а ячейки, разумеется, имеют иерархическую структуру: "Зона склада" -> Стеллаж -> Полка -> Ячейка.
Ну и вишенкой на торте является маркировка товаров: все упаковки и коробки пронумерованы, а в БД хранится информация об их вложенности. Это используется для своеобразной отчётности в государственном мониторинге лекарственных препаратов.
Это было бы интересно почитать в виде отдельной статьи?

vagon333
24.06.2022 16:50+1В моем случае масса деревьев (MSSQL).
Нужно простое решение по созданию, заполнению и начитке.Последние 15+ лет использую Adjacency List.
Лет 10 назад перешел с рекурсивного CTE на динамически создаваемый запрос через SQL CLR с возможность фильтровать и сортировать отдельно по корневой в вложенной ветке.Полет нормальный, проблем с производительсностью нет, а структура дерева максимально простая.

tmk826
25.06.2022 01:12+1Используем Adjacency List для хранения дерева файловой системы (порадка 10^9 файлов) . Плюс: быстрый листинг директории и перемещение файлов. Минус: нужна рекурсия чтобы достать ветку дерева.
Вариант с Closure Table создаёт неоправданно много записей для сильмп вложенных путей.

PaulZi
25.06.2022 13:05Я пришел к выводу что лучше всего комбинировать AL+MP, это даёт лёгкое получение всех основных операций, а из недостатков - только сложности с обновлением детей родителя при его перемещении, что обычно не очень частая операция, которая к тому же легко выполняется за счёт индекса.
NS - вообще годится только для маленьких деревьев, так как вставка в начало большого дерева - это дикая боль, пересчитывающее все дерево.

PaulIsh
26.06.2022 14:50Для деревьев использовали внешнюю таблицу на основе AL+MP + добавляли childIndex для сортировки детей. Если нужно было объединять в иерархию несколько сущностей (таблиц), то вместо одной ссылки на таблицу сущностей добавлялось больше столбцов-ссылок. Непротиворечивость ссылок в рамках одной записи обеспечивалось дополнительным столбцом с индексом сущности.
Создание иерархии во внешней таблице позволяет избежать модификации основный таблиц и строить больше одной иерархии на основе базовой таблицы. Недостатком такого подхода является необходимость поддерживать актуальность иерархических таблиц вместе с основными.


vagon333
@MericaDotNet,
Сейчас в новостях Хабра ваша статья размещена полностью и раздражает излишним размером.
Пока вам не опустили рейтинг ниже плинтуса, разделите пож. вашу статью, чтоб над катом была малая часть, дающая представление о содержании, а под катом полная статья.
MericaDotNet Автор
Исправлено.