Приветствую Вас, Хабровчане!
Я думаю, по названию статьи и так понятно о чем я Вам буду рассказывать в этой работе. Поэтому не вижу смысла в длинных преамбулах и аннотациях. Ну а для тех, кто совсем не в теме и фамилию известного нидерландского ученого видят впервые — отправляю Вас на википедию с его биографией и алгоритмом, о котором далее пойдет речь.
И да, я прекрасно понимаю, что я далеко не первый и не последний кто находит в себе силы попробовать на практике реализовать этот алгоритм. Как говорится, повторение — мать учения. Поэтому не нужно меня за это закидывать камнями, палками и чем бы то ни было. Я лишь предложу свой вариант реализации и продемонстрирую результаты. Как Вы уже догадались, писать будем на языке C#. Исходники найдете здесь.
Поехали!
Содержание
Математическая постановка задачи
В декартовой прямоугольной системе координат на плоскости задана равномерная сетка:
где — узлы сетки;
— шаги сетки;
— количество точек по оси
и
, соответственно. В каждом узле сетки задано значение
, представляющее собой высоту карты (ландшафта) местности в рассматриваемой точке. Значения
, образующие исследуемую поверхность, могут быть отрицательными — в таком случае высоту карты следует понимать как глубину относительно некоторой нулевой отметки
.
Заданы стартовая и целевая точка искомого оптимального маршрутаи
, рисунок 1.
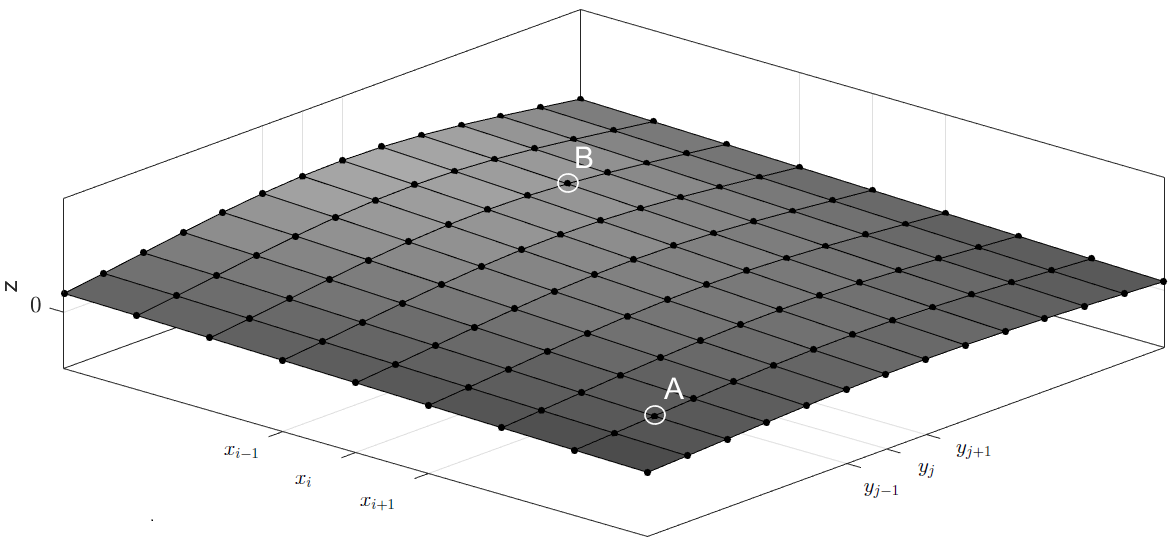
На выходе мы должны получить конечный список (массив) координат, следуя по которым мы доберемся из точки
в точку
наиболее оптимальным образом.
Также в алгоритме будет учитываться параметр, задающий максимальный угол уклона (в градусах) для поиска подходящих соседей.
Так, ну а при чем тут графы и какой-то алгоритм ?!
Графы и алгоритм Дейкстры
Алгоритм Дейкстры представляет собой глобальный алгоритм поиска кратчайших путей на взвешенном графе. О том, что такое граф, и с чем его едят, что такое вершина, ребро, какие графы бывают — я здесь Вам рассказывать не буду. На тему графов написано немало хороших книг, на одну из которых я дам ссылку в конце статьи. А пока я буду предполагать, что Вы уже знакомы с основными понятиями теории графов. Хотя, как по мне, большинство терминов, которые будут описаны далее в статье должны быть понятны и ежу на интуитивном уровне.
Как я упомянул выше, алгоритм Дейкстры является глобальным, я бы даже сказал самым глобальным из всех подобных. Имеются и другие алгоритмы, которые в ряде случаев оптимизируют и ускоряют поиск, например, такие как алгоритм Ли, алгоритм A* и др. Очень хороший обзор на алгоритмы поиска (в т.ч. и Дейкстры) да еще и с примерами кода можете найти тут.
Ну а я просто захотел попробовать сделать это своими силами. Как говорится, хочешь сделать что-то хорошо - сделай это сам! =)
Так в чем же именно глобальность алгоритма Дейкстры?! Глобальность в том, что даже если нам будет необходимо найти кратчайший путь между двумя смежными вершинами графа, в котором 1000 вершин, нам так или иначе придется перебрать абсолютно все 1000 вершин.
Поясню это на примере взвешенного графа с 6-ю вершинами, рисунок 2.
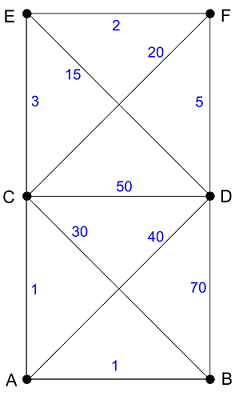
Найдем кратчайший путь из вершиныдо вершины
. Даже не "запуская" на этом графе алгоритм Дейкстры, очевидно, что кратчайший путь из
в
будет путь
, длина которого равна
. Так вот, несмотря на то, что вершины
и
смежные — нам все равно пришлось рассматривать ВСЕ вершины этого графа. В этом и заключается глобальность, и в то же время сложность этого алгоритма (я специально подобрал весовые коэффициенты для некоторых ребер намного большими чем другие).
Превращаем поверхность в граф
Чтобы решить нашу задачу с помощью алгоритма Дейкстры нам нужно каким-то образом "превратить" нашу исследуемую поверхность во взвешенный граф. Делать будем это так, — посмотрим на нашу поверхность сверху (перпендикулярно плоскости ), вид будет примерно такой, рисунок 3:
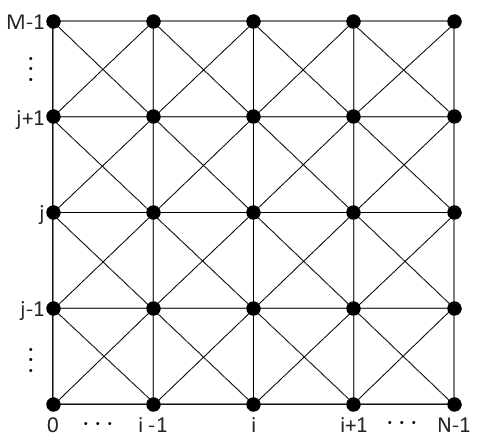
Точки поверхности будут спроецированы на плоскость— это и будут вершины нашего графа. Но откуда появились эти "крестики" в каждом квадратике, спросите Вы ?! Эти крестики — тоже ребра графа, которые добавлены для того, чтобы у нас была возможность ходить не только по горизонтали и вертикали, но и по диагонали. Да, это сильно увеличит сложность алгоритма и время расчета, но зато путь будет еще более оптимальным.
Таким образом любую вершину подобного графа можно идентифицировать с помощью координаты , что нам очень пригодится в дальнейшем для хранения всех вершин графа в виде матрицы.
Наш граф должен быть взвешенным. Вот тут, конечно, можно поиграться и задавать весовые коэффициенты любым изощренным способом. Но я пока поступлю просто — весребра, соединяющего смежные вершины
и
, заданные своими координатами
будет не что иное как расстояние в пространстве между соответствующими точками поверхности, из которой наш граф был построен:
Рассматриваемый граф является связным (причем степень связности достаточно неплохая!, особенно после добавления диагональных ребер), поэтому "тупиковых" ситуаций возникнуть не должно и если все учтено правильно, алгоритм все-таки после долгих блужданий доберется из стартовой в целевую вершину и на своем пути "переберет" абсолютно все вершины графа.
Ну все...осталось запустить алгоритм Дейкстры!
Само собой при численной реализации этого алгоритма возникнут определенные сложности много костылей и вопросы. Их я уже буду комментировать в процессе объяснения написанного кода.
Численная реализация
Кодить, как я уже говорил будем на C#, поэтому постараемся взять все самое лучшее из возможностей этого языка. А возможностей у него немало.
Я создам в Visual Studio консольный проект (.NET 4.7.2). Ключевыми классами будут Point2D.cs, Vertex.cs и Graph.cs. Начнем с самого простого.
Класс Point2D будет содержать всего два свойства для хранения координат вершины графа:
public class Point2D
{
public int i { get; }
public int j { get; }
public Point2D(int i, int j)
{
this.i = i;
this.j = j;
}
}С классом Vertex уже чуть поинтереснее:
public class Vertex
{
public Point2D Coordinate { get; set; }
public double Height { get; set; }
public Point2D CameFrom { get; set; }
public double Label { get; set; }
public bool IsVisited { get; set; }
public bool IsGoal { get; set; }
public bool IsObstacle { get; set; }
public Vertex(int i, int j, Point2D CameFrom = null, double Height = 0.0, double Label = double.MaxValue, bool IsVisited = false, bool IsGoal = false, bool IsObstacle = false)
{
Coordinate = new Point2D(i, j);
this.CameFrom = CameFrom;
this.Height = Height;
this.Label = Label;
this.IsVisited = IsVisited;
this.IsGoal = IsGoal;
this.IsObstacle = IsObstacle;
}
}Опишу кратко свойства.
Первое из них — это координаты вершины графа; Height — высота, значение функции в точке вершины, необходимое для расчета весового коэффициента и величины уклона между двумя смежными вершинами; CameFrom — здесь в процессе работы алгоритма будут храниться координаты вершины из которой мы попали в текущую вершину — на основании этого свойства мы в конце работы алгоритма сформируем наш искомый маршрут; Label — метка, хранящая значение длины пути из стартовой вершины в текущую; IsVisited — говорит нам посетили ли мы данную вершину в процессе расчета или нет; IsGoal — данное свойство будет истинным только для целевой вершины графа (та вершина, оптимальный путь к которой мы ищем). Это свойство понадобилось мне для того, чтобы алгоритм Дейкстры не завершился раньше времени и мы обошли абсолютно все вершины графа; IsObstacle — наш алгоритм будет также уметь обходить препятствия, например, искать кратчайший путь в лабиринте, это свойство позволяет задать определенные вершины как вершины-препятствия, чтобы выбрасывать их из рассмотрения наряду с уже посещенными.
Теперь о классе Graph.
Свойства класса Graph:
public class Graph
{
/// <summary>
/// Шаг сетки по оси Ox
/// </summary>
public double dx { get; }
/// <summary>
/// Шаг сетки по оси Oy
/// </summary>
public double dy { get; }
/// <summary>
/// Количество вершин по оси Ox
/// </summary>
public int N { get; }
/// <summary>
/// Количество вершин по оси Oy
/// </summary>
public int M { get; }
/// <summary>
/// Матрица вершин графа
/// </summary>
public Vertex[,] Vertices { get; }
/// <summary>
/// Предельная величина уклона, необходимая для обхода препятствий, в градусах
/// </summary>
public double MaxSlope { get; }
}Для работы алгоритма реализуем несколько вспомогательных методов.
Для расчета весов и уклона нам нужно будет получать "реальные" координаты вершины графа на плоскости (с учетом величины шагов
и
):
(double, double) GetRealXY(Vertex vertex)
{
double x = vertex.Coordinate.i * dx;
double y = vertex.Coordinate.j * dy;
return (x, y);
} Вес ребра между смежными вершинами (расстояние между точками поверхности) находим так:
double Weight(Vertex v1, Vertex v2)
{
(double, double) x1y1 = GetRealXY(v1);
(double, double) x2y2 = GetRealXY(v2);
double xDiff = x1y1.Item1 - x2y2.Item1;
double yDiff = x1y1.Item2 - x2y2.Item2;
double zDiff = v1.Height - v2.Height;
double sumOfSquares = Math.Pow(xDiff, 2.0) + Math.Pow(yDiff, 2.0) + Math.Pow(zDiff, 2.0);
return Math.Sqrt(sumOfSquares);
}Следующий метод возвращает величину уклона между смежными вершинами (в градусах):
private double Slope(Vertex v1, Vertex v2)
{
double hypotenuse = Weight(v1, v2); // Вес ребра - это и есть по факту расстояние между точками
double zDiffAbs = Math.Abs(v1.Height - v2.Height); // Модуль разности по высоте
return Math.Asin(zDiffAbs / hypotenuse) * 180.0 / Math.PI; // Переводим радианы в градусы
} Для удобства реализуем 8 методов для получения соседней вершины в зависимости от направления (я привел один из них):
private Vertex GetTopVertex(Vertex v) => Vertices[v.Coordinate.i, v.Coordinate.j + 1];И еще 8 методов для определения принадлежности вершины той или иной части сетки (здесь я привел два из них):
private bool IsTopRightVertex(Vertex v1) => v1.Coordinate.i == N - 1 && v1.Coordinate.j == M - 1;
private bool IsVertexOnTheRightSide(Vertex v1) => v1.Coordinate.i == N - 1;Эти методы понадобятся для получения всех смежных вершин для рассматриваемой вершины. Вот тут нам придется нарубить if-ов, т.к. количество смежных вершин не всегда одно и то же:
Метод GetAllAdjacentVertices(Vertex vertex) для получения всех смежных вершин
private List<Vertex> GetAllAdjacentVertices(Vertex vertex)
{
#region Рассматриваем угловые вершины
if (IsTopRightVertex(vertex))
return new List<Vertex>
{
GetLeftVertex(vertex),
GetBottomLeftVertex(vertex),
GetBottomVertex(vertex)
};
if (IsBottomRightVertex(vertex))
return new List<Vertex>
{
GetTopVertex(vertex),
GetTopLeftVertex(vertex),
GetLeftVertex(vertex)
};
if (IsBottomLeftVertex(vertex))
return new List<Vertex>
{
GetTopVertex(vertex),
GetTopRightVertex(vertex),
GetRightVertex(vertex)
};
if (IsTopLeftVertex(vertex))
return new List<Vertex>
{
GetBottomVertex(vertex),
GetBottomRightVertex(vertex),
GetRightVertex(vertex)
};
#endregion
#region Рассматриваем боковые вершины
if (IsVertexOnTheTopSide(vertex))
return new List<Vertex>
{
GetLeftVertex(vertex),
GetBottomLeftVertex(vertex),
GetBottomVertex(vertex),
GetBottomRightVertex(vertex),
GetRightVertex(vertex)
};
if (IsVertexOnTheRightSide(vertex))
return new List<Vertex>
{
GetTopVertex(vertex),
GetTopLeftVertex(vertex),
GetLeftVertex(vertex),
GetBottomLeftVertex(vertex),
GetBottomVertex(vertex)
};
if (IsVertexOnTheBottomSide(vertex))
return new List<Vertex>
{
GetLeftVertex(vertex),
GetTopLeftVertex(vertex),
GetTopVertex(vertex),
GetTopRightVertex(vertex),
GetRightVertex(vertex)
};
if (IsVertexOnTheLeftSide(vertex))
return new List<Vertex>
{
GetTopVertex(vertex),
GetTopRightVertex(vertex),
GetRightVertex(vertex),
GetBottomRightVertex(vertex),
GetBottomVertex(vertex)
};
#endregion
// Иначе вершина лежит "в середине карты" и нужно вернуть все 8 смежных вершин
return new List<Vertex>
{
GetTopVertex(vertex),
GetRightVertex(vertex),
GetBottomVertex(vertex),
GetLeftVertex(vertex),
GetTopRightVertex(vertex),
GetBottomRightVertex(vertex),
GetBottomLeftVertex(vertex),
GetTopLeftVertex(vertex)
};
}Напишем метод, который будет "отсеивать неподходящих" соседей:
private List<Vertex> GetValidNeighbors(Vertex current)
{
// Из всех смежных вершин оставляем только те, которые
// 1. Еще не посещены
// 2. Не являются вершинами-препятствиями
// 3. Наклон к которым меньше заданной величины (например, 30 градусов)
return GetAllAdjacentVertices(current).Where(v => !v.IsVisited && !v.IsObstacle && Slope(v, current) < MaxSlope).ToList();
}и метод, который из оставшихся соседей будет отсеивать целевую вершину и сообщать осталось ли что-то после отсеивания:
private bool HasValidAndNotGoalNeighbors(Vertex vertex, out List<Vertex> validAndNotGoalNeighbors)
{
validAndNotGoalNeighbors = GetValidNeighbors(vertex).Where(v => !v.IsGoal).ToList();
return validAndNotGoalNeighbors.Any();
}Именно этот метод (в основном) и нужен для того, чтобы мы перебрали абсолютно все вершины графа (помните о глобальности, да??!). Так как бывают кейсы, когда мы натыкаемся на целевую вершину "раньше срока" (раньше того, как алгоритм пробежит по всем вершинам графа и найдет нам оптимальный маршрут).
Также в основном while-цикле метода по поиску пути (скоро мы уже дойдем до него =)) я буду накапливать в список посещенные вершины. Это тоже относится к замечанию выше и будет гарантировать нам "полный обход" всех вершин графа. Этот список посещенных вершин я буду использовать в следующем методе.
Метод для получения новой "текущей" вершины:
GetCurrent(List<Vertex> visitedVertices)
private Vertex GetCurrent(List<Vertex> visitedVertices)
{
List<Vertex> validAndNotGoalNeighbors = new List<Vertex>();
foreach (Vertex v in visitedVertices)
if (HasValidAndNotGoalNeighbors(v, out validAndNotGoalNeighbors))
break;
// Если не нашлось ни одного подходящего соседа, значит мы дошли
// до целевой вершины. Алгоритм завершен
if (!validAndNotGoalNeighbors.Any())
return null;
// Иначе находим и возвращаем соседа с минимальной меткой
double minLabel = validAndNotGoalNeighbors.Min(v => v.Label);
Vertex newCurrent = validAndNotGoalNeighbors.First(v => v.Label == minLabel);
return newCurrent;
}И вот он!! Метод для поиска кратчайшего (оптимального) пути (и его длины):
public List<Point2D> FindShortestPathAndLength(Point2D startPoint, Point2D goalPoint, out double shortestPathLength)
{
shortestPathLength = 0.0;
// Стартовой вершине присваиваем нулевую метку
Vertex start = Vertices[startPoint.i, startPoint.j];
start.Label = 0.0;
// Целевую вершину пометим, что она целевая
Vertex goal = Vertices[goalPoint.i, goalPoint.j];
goal.IsGoal = true;
// Помечаем стартовую вершину как текущую
Vertex current = start;
// В этом списке будем копить посещенные вершины
List<Vertex> visitedVertices = new List<Vertex>();
while (current != null)
{
// Находим подходящих (годных) соседей: которые еще не посещены, не являются препятствиями и т.п.
List<Vertex> neighbors = GetValidNeighbors(current);
foreach (Vertex neighbor in neighbors)
{
double currentWeight = current.Label + Weight(current, neighbor);
if (currentWeight < neighbor.Label)
{
neighbor.Label = currentWeight;
neighbor.CameFrom = current.Coordinate;
}
}
// После того как все подходящие соседи рассмотрены (им расставлены метки), помечаем текущую вершину как посещенную
current.IsVisited = true;
// и добавляем ее в список посещенных вершин
visitedVertices.Add(current);
// Используем этот список посещенных вершин для поиска новой текущей вершины
current = GetCurrent(visitedVertices);
}
// В конце работы алгоритма в целевой вершине в свойстве Label будет находиться длина искомого пути
shortestPathLength = goal.Label;
// Основываясь на свойстве CameFrom сформируем и вернем сам искомый путь
return GetShortestPath(goal);
}Следующий метод на основе свойства CameFrom класса Vertex "собирает" и возвращает нам искомый путь:
GetShortestPath(Vertex goal)
private List<Point2D> GetShortestPath(Vertex goal)
{
List<Point2D> path = new List<Point2D>();
path.Add(goal.Coordinate);
Point2D cameFrom = goal.CameFrom;
while (cameFrom != null)
{
Vertex vertex = Vertices[cameFrom.i, cameFrom.j];
path.Add(vertex.Coordinate);
cameFrom = vertex.CameFrom;
}
return path;
}Надо заметить, что массив, содержащий координаты искомого маршрута будет сформирован "задом на перед". Т.е. первым элементом массива будут координаты целевой вершины, а последним элементом — координаты стартовой.
Ну вот, в принципе, и все!
Весь остальной код, классы и методы, — являются вспомогательными (вычисление двумерного Гауссиана, запись/чтение из файла и т.п.). Если Вы дошли до этого абзаца и хорошо понимаете, что происходит, остальную часть, я думаю, понять Вам не составит труда. Поэтому не буду на нем останавливаться, тем более что код подробно прокомментирован.
Стоит, наверное, все-таки упомянуть о двух перегруженных конструкторах класса Graph, один из которых инициализирует граф с помощью поверхности (для расчетов я использовал только Гауссиан, можете поиграться с другими поверхностями), а другой конструктор инициализирует граф с помощью матрицы из нулей и единичек (матрица-препятствий) для создания сложных лабиринтов.
Давайте наконец посмотрим на результаты!
Результаты расчетов. Простые препятствия
Начнем с простого примера. Создадим на сетке небольшое вертикальное препятствие, рисунок 4, и позволим алгоритму обойти его:
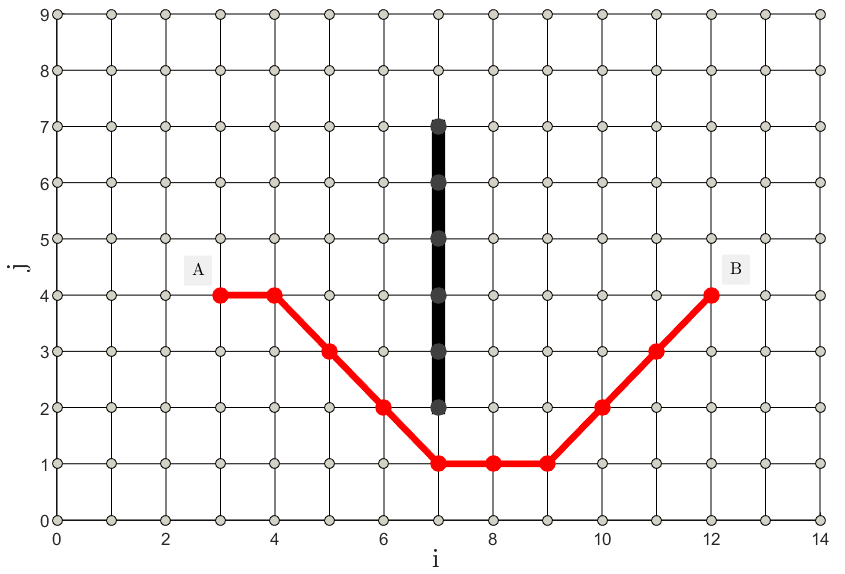
Вершины графа, которые попадают под черную линию имеют свойство IsObstacle = true, чтобы пометить их как вершины-препятствия. Параметр уклона MaxSlope здесь не имеет смысла, т.к. алгоритм работает в одной плоскости. Как видите, результат очень правдоподобный.
Из архива. Как я формировал это препятствие в csv-файле. Координаты пути
Для чтения матрицы из csv-файла и других вспомогательных действий создан класс Obstacle.
Рассмотрим следующий пример, рисунок 5:

В данном случае я бы не сказал, что это является ошибкой, ведь алгоритм учитывает как препятствие только те вершины графа, которые непосредственно помечены как вершины-препятствия (IsObstacle = true).
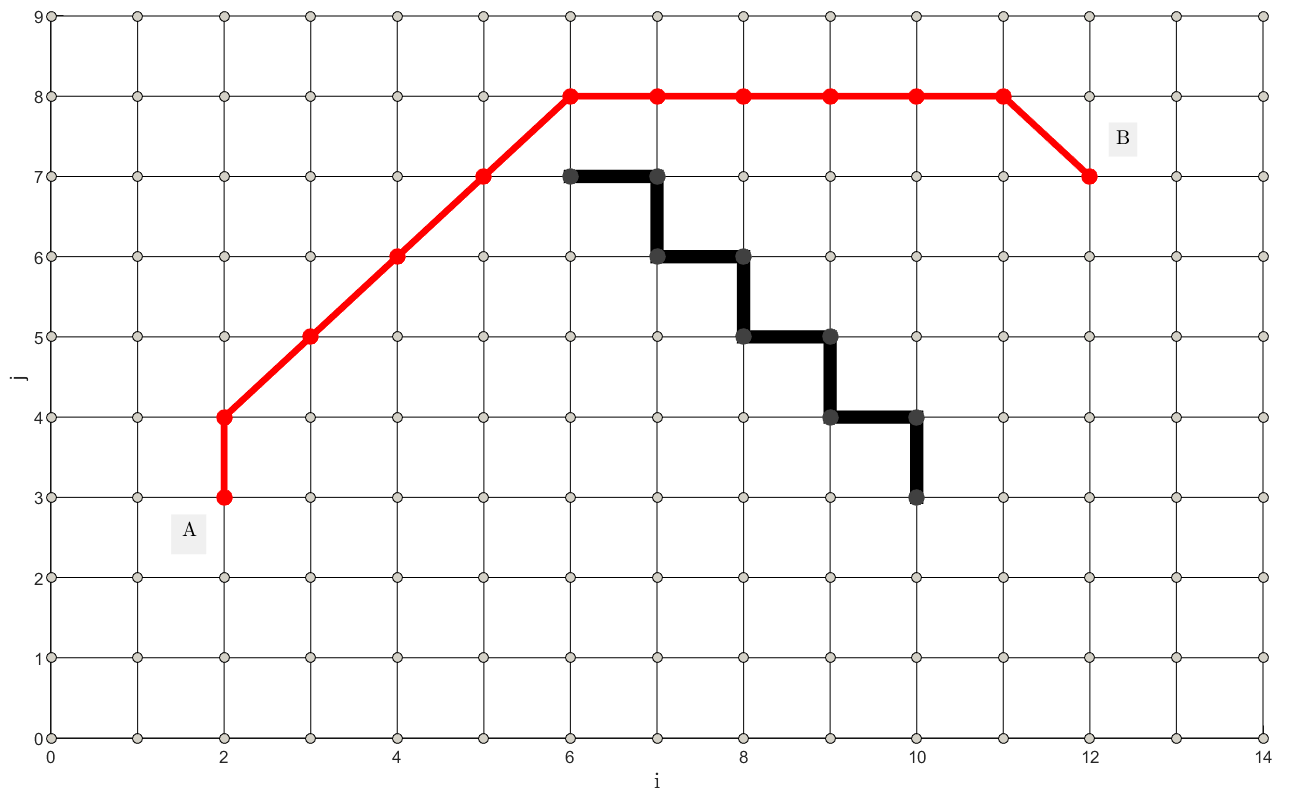
А вот если мы сформируем препятствие вот так, тогда алгоритм никуда не денется и ему придется его обойти, рисунок 6:
Лабиринты
Усложним работу для алгоритма и сформируем для него целый лабиринт препятствий, рисунок 7:
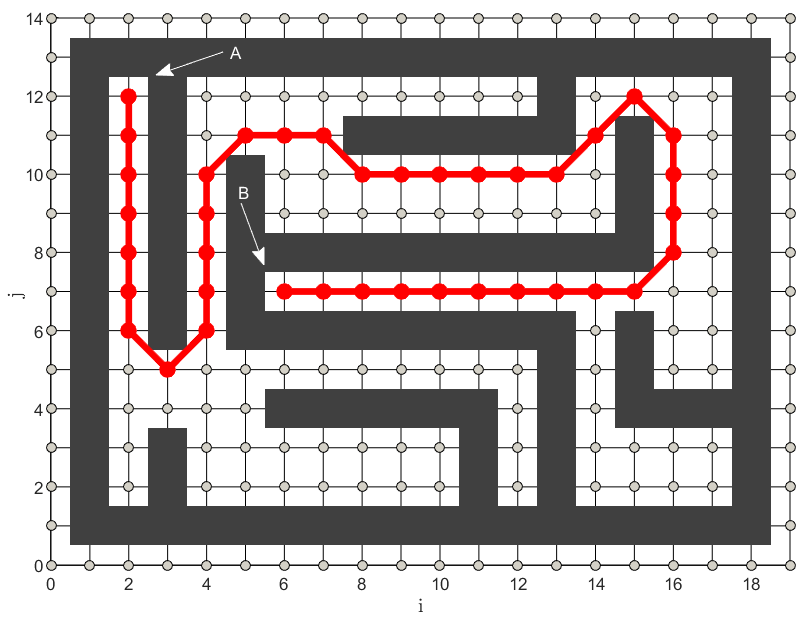
Увеличим лабиринт и изменим целевую вершину, рисунок 8:
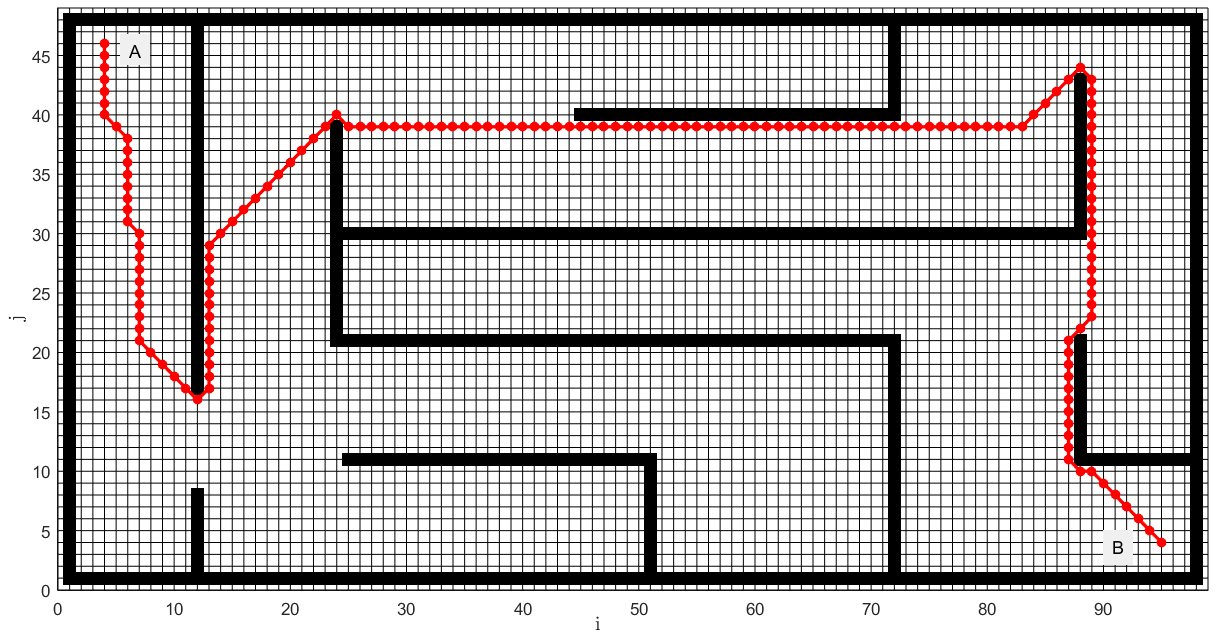
Все исходные файлы по которым были построены все вышеперечисленные препятствия и лабиринты, а также координаты найденных путей находятся в проекте в соответствующих папках.
Поиск оптимального пути на поверхности
Ну и в конце приведу пример поиска оптимального пути между двумя точками на сложной поверхности. Именно оптимального, т.к. нельзя сказать, что он кратчайший, рисунок 9:
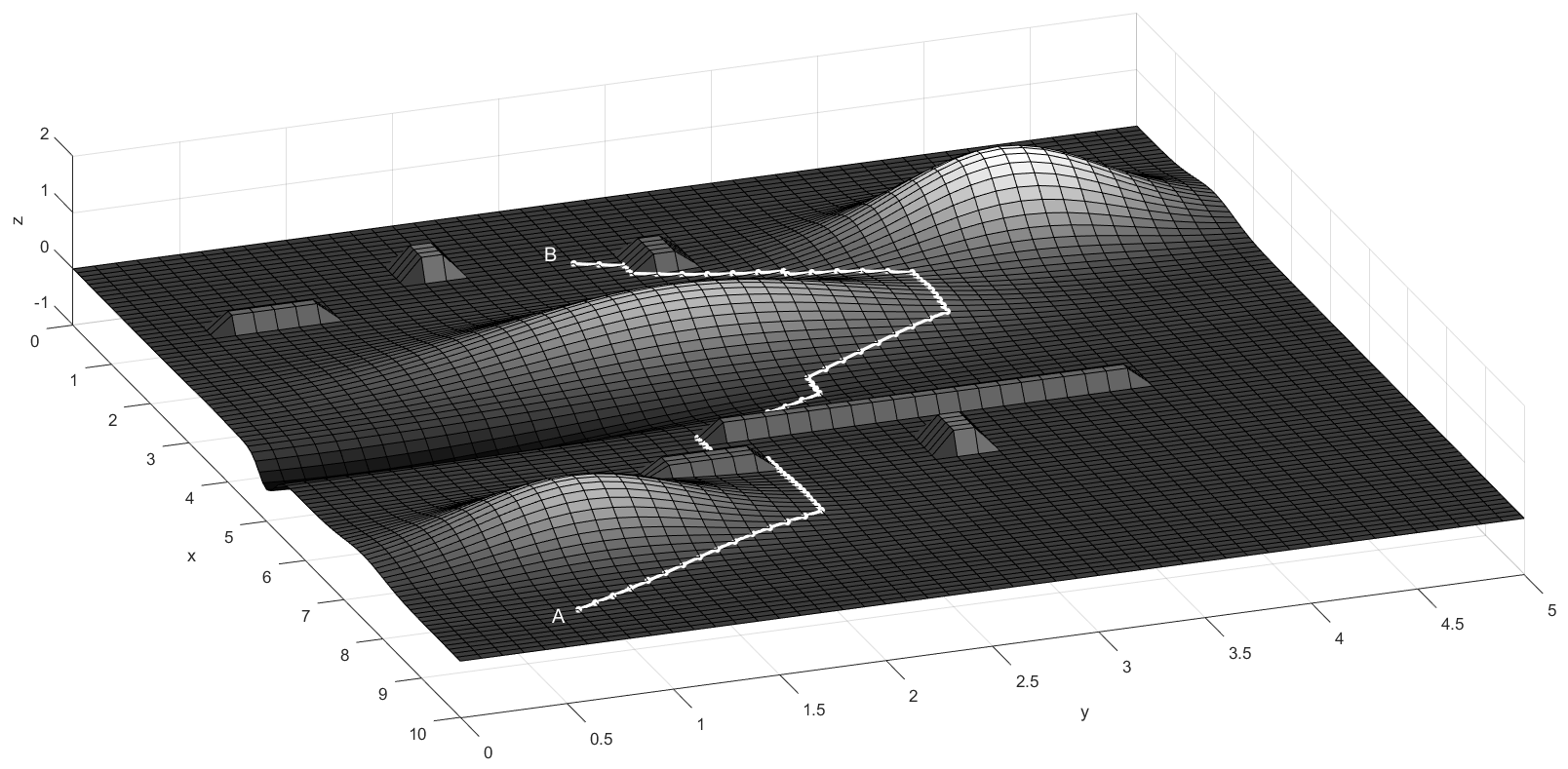
Для имитации холмов и оврага были использованы двумерные функции Гаусса с различными параметрами. Для имитации искусственных сооружений в класс Graph был добавлен метод:
CreateBuilding()
public void CreateBuilding(Point2D bottomLeftCoordinate, int width, int length, double height)
{
for (int i = bottomLeftCoordinate.i; i < bottomLeftCoordinate.i + width; i++)
{
for (int j = bottomLeftCoordinate.j; j < bottomLeftCoordinate.j + length; j++)
Vertices[i, j].Height = height;
}
}Замечу, что здесь ни одна вершина графа не помечена как препятствие, алгоритм находит оптимальный путь благодаря заданию параметра MaxSlope. Если задать параметр MaxSlope очень большим — алгоритм может пойти прямиком через горы.
И еще картинки с других ракурсов.
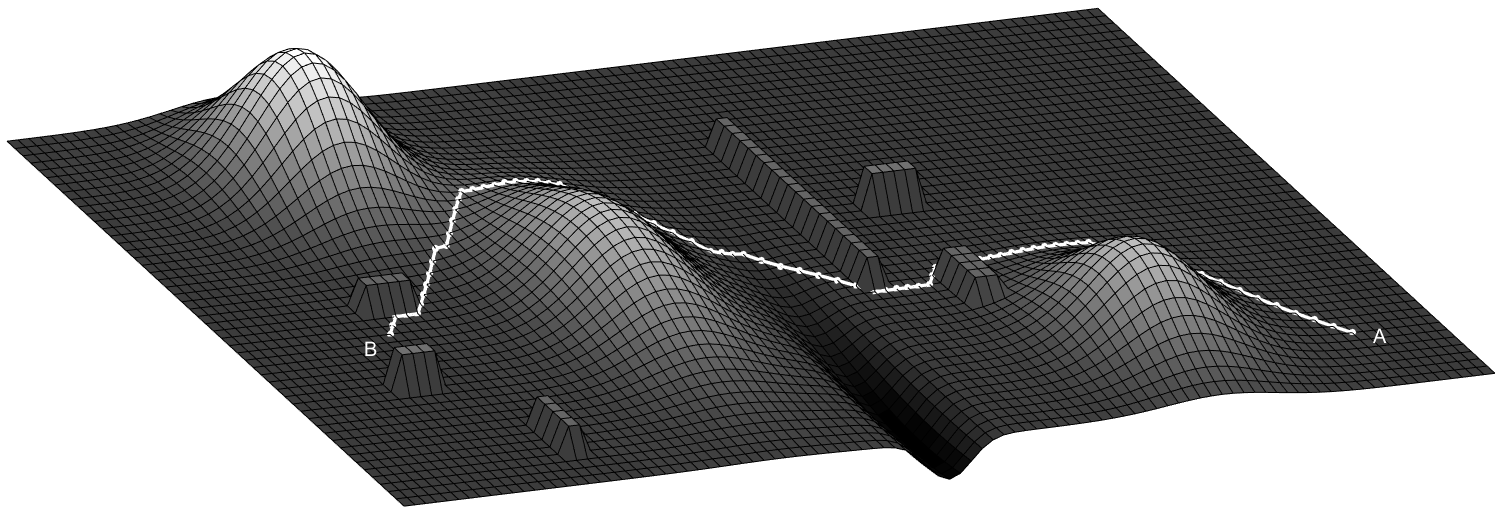
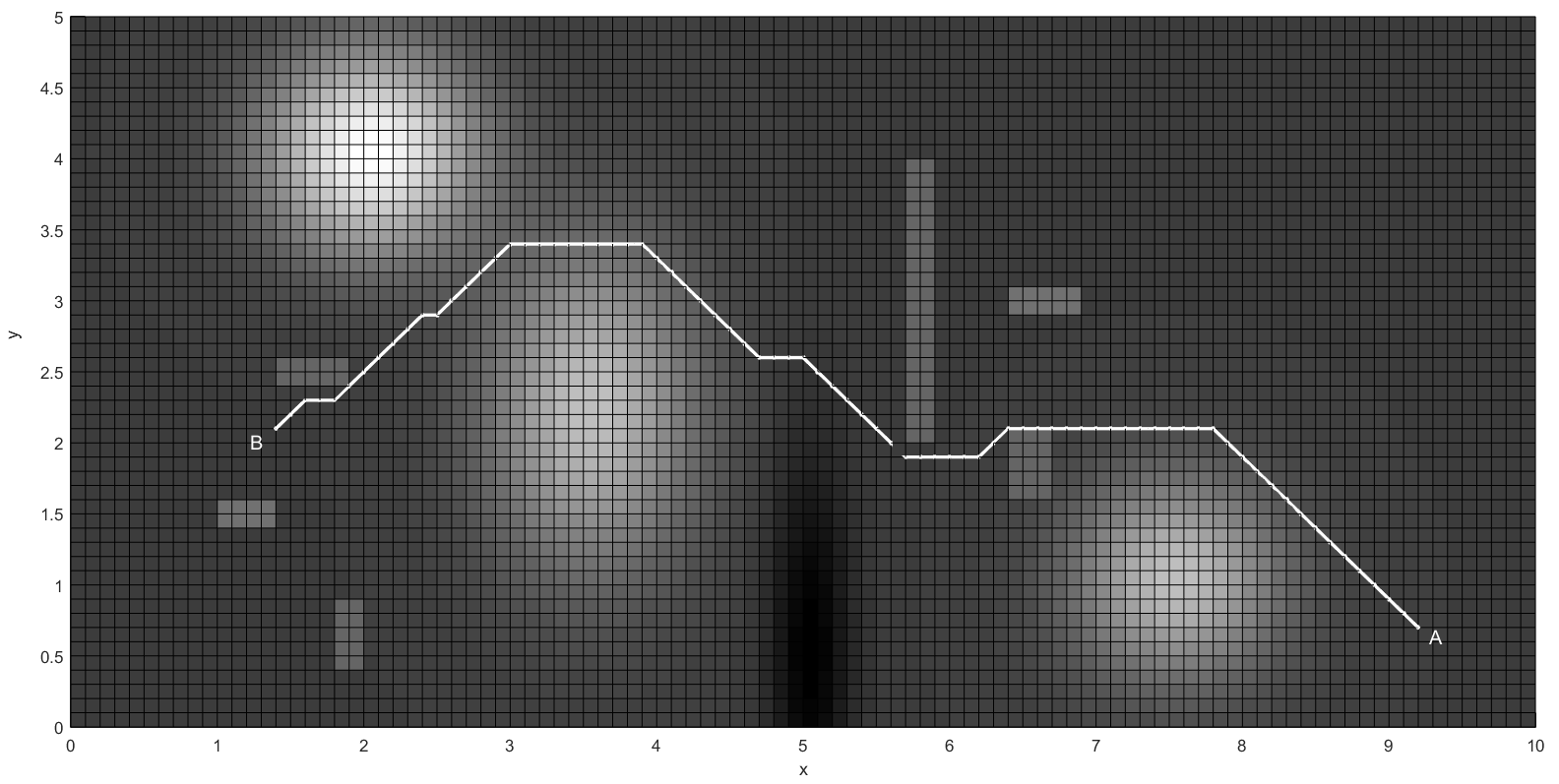
Заключение
Спасибо за прочтение!
Надеюсь статья была интересной и полезной. Все доработки и оптимизацию алгоритма оставляю Вам.
Литература:
Робин Уилсон. Введение в теорию графов. Пятое издание. 2019
Всем добра и качественного кода!
Комментарии (29)

wataru
16.11.2022 16:54-1Поиск по поверхности работает не правильно. Ведь можно не только ходить по диагонали внутри квадрата, но пройтись по диаганали, скажем, в прямоугольнике 1x2. И это будет короче, чем идти по ломанной. На самом деле, из-за трехмерности и разных наклонов плоскостей будет какой-то излом, но он будет внутри границы ячеек, а не в углах.
Для плоских лабиринтов лучше применять какую-нибудь вариацию A*, например, jump point search, а не Дейкстру.
И Дейскстра, кстати, с ошибкой написана. Смысл исключать в validAndNotGoalNeighbors те вершины, которые связаны только с goal? Почитайте, что ли, описание алгоритма по своим ссылкам. Там всегда берется минимальная вершина из пока еще не зафиксированных, от нее производится релаксация на всех соседей, и вершина фиксируется. Нигде не фигурирует "но исключить из рассомотрения ребра к ответу".
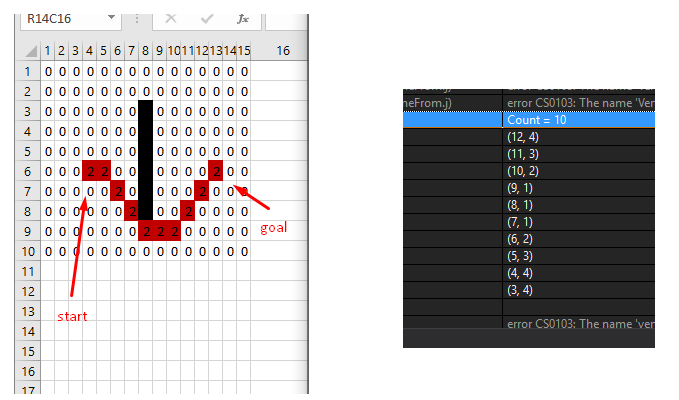
Например, я не верю, что ваша программа находит путь на рисунке 7 в лабиринте. Ибо там предпоследняя врешина в ответе связана только с goal из не посещенных вершин. И она никогда не станет current и путь из нее в goal никогда не будет подсчитан.
Если это была такая попытка устроить ранний выход из алгоритма, когда уже нашли расстояние до финиша, то на правильно это делается так: остановитесь, когда пометили goal isVisited.
Плюс это усложняет алгоритм. Не надо никакие вершины isVisited или isGoal исключать. Ну прорелаксируете вы ребро к уже зафиксированной вершине — уже найденный путь к ней будет короче и ничего не поменяется. Вы на этих фильтрациях списков, наверно, столько времени теряете. В итоге и код будет сильно короче и понятнее, и работать будет быстрее.

Green21 Автор
16.11.2022 17:42Например, я не верю, что ваша программа находит путь на рисунке 7 в лабиринте. Ибо там предпоследняя врешина в ответе связана только с goal из не посещенных вершин. И она никогда не станет current и путь из нее в goal никогда не будет подсчитан.
А здесь не нужно верить или не верить. Нужно просто взять и проверить. Так уж и быть, сделаю это за Вас. Алгоритм корректно находит путь в этом лабиринте (см. скрин). И длина пути правильная
Скрин
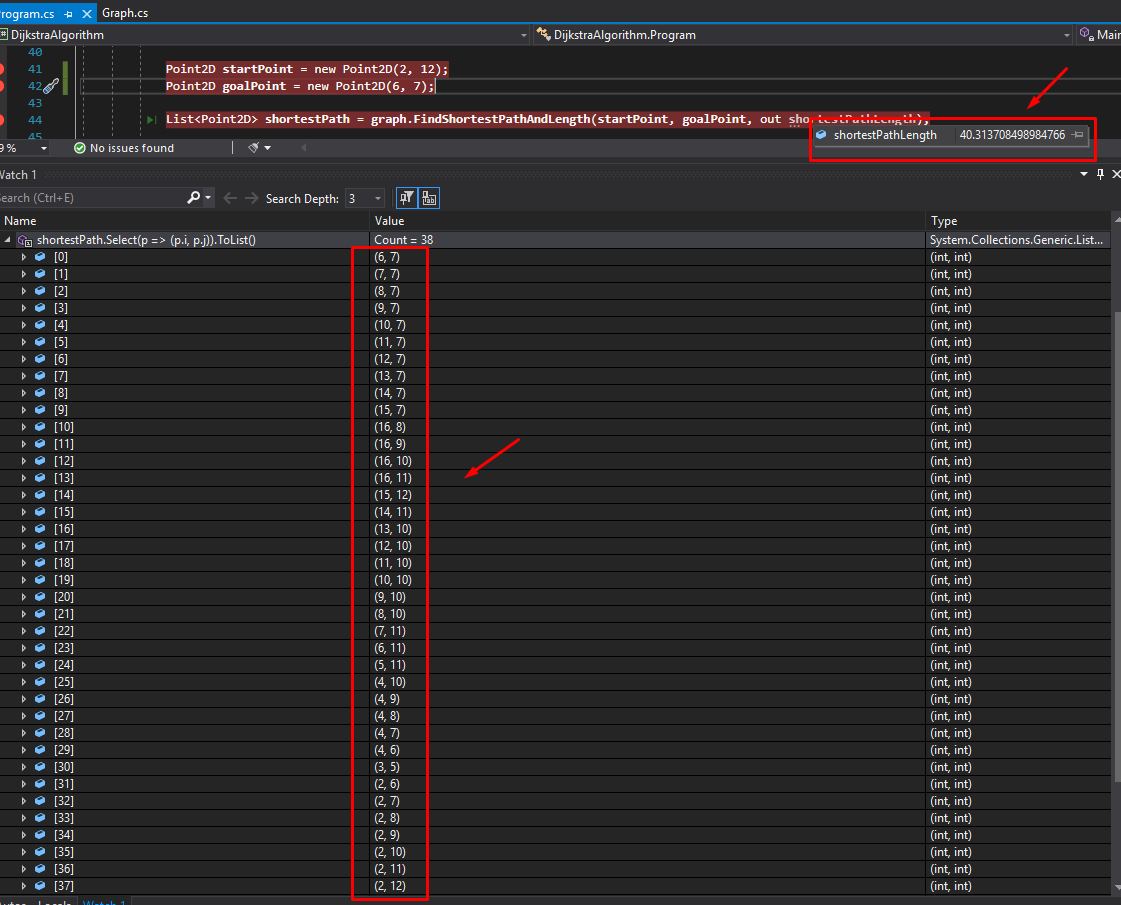
Если это была такая попытка устроить ранний выход из алгоритма
Никакого раннего выхода тут нет. Наоборот, я пытаюсь заставить алгоритм не выходить раньше времени, о чем я и написал в статье.
Поиск по поверхности работает не правильно
Что значит "не правильно" ? Это один из вариантов реализации. Да, возможно стоить рассматривать прямоугольники 2 на 1. Попробуйте реализовать свой вариант.
Поэтому не стоит так критиковать, если Вы сами ни разу не пробовали реализовывать данный алгоритм.

wataru
16.11.2022 18:40+1А здесь не нужно верить или не верить. Нужно просто взять и проверить.
Да, тут был не прав. У вас так странно написано, что я запутался. Вы оказывается берете минимальную непосещенную вершину среди соседей какой-то одной "посещенной" каждый раз. А надо среди всех не посещенных вершин.
Вот вам тест:
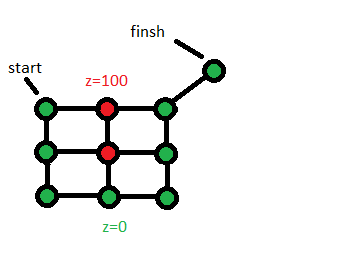
10 вершин не-препядствий в квадрате 3x3 плюс goal висит сбоку по диагонали (остальные вершины вокруг — препядствия). Все вершины, кроме (1,0) и (1,1) имеют z координату 0, а эти две — очень большую z координату (100, например). Разрешите в этом тесте любой slope. Ваша программа же должна работать с любыми ограничениями? Но вообще, этот тест можно усложнить и сделать так, что с минималным изменением z координаты у вас будет все плохо.
Ответ тут — обойти гору по зеленым вершинам за 2+3sqrt(2). Вы же найдете ответ больше 200.
Потому что сначала вы возьмете в качестве current вершину в координатах (0,0,0). Потом в (1,0,0), потом в (0,1,100). Вот тут у вас ошибка. Эту вершину нельзя фиксировать, ибо до нее расстояние пока не минимальное из всех соседних с isVisited. Потом вы возьмете вершину (2,0,0) снизу. И потом (0, 2, 0) — но с расстоянием больше 200. Все. Вот тут вы уже посчитаете расстояние для goal и больше никогда его не пересчитаете, потому что его можно только через эту вершину посчитать но она уже помечена isVisited и никогда current не будет.
Похоже вы с этой проблемой уже в разработаке столкнулись и именно в попытке ее решить и воткнули этот костыль с особым рассмотрением isGoal вершины. Но это не решает проблемы. В итоге у вас получилось что-то вроде гибрида дейкстры и обхода в ширину и на некоторых тестах оно даже работает.
Никакого раннего выхода тут нет. Наоборот, я пытаюсь заставить алгоритм не выходить раньше времени, о чем я и написал в статье.
Но алгоритм дейкстры (описанный в википедии, на пример) и не выходит раньше времени. Он останавливается, когда найдет расстояние до всех достижимых вершин. В алгоритме Дейкстры вообще нет понятия одного goal — он ищет путь до всех вершин сразу. Поэтому как-то отдельно выделять конечную вершину в коде — не надо.
Что значит "не правильно"?
Значит находит не кратчайший маршрут, потому что кратчайший маршрут может идти не только по границам сетки и диагоналям в квадратах.
Поэтому не стоит так критиковать, если Вы сами ни разу не пробовали реализовывать данный алгоритм.
Не надо так болезненно реагировать на критику и пытаться всякие "сперва-добейся" применять. Я с медалями с чемпионатов мира про программированию и далеко не только Дейкстру реализовывал столько раз, сколько вы программ в своей жизни не написали.

Green21 Автор
16.11.2022 19:10-2Вот вам тест
Видимо мы недопоняли друг друга.
Такие графы, которые вы привели в качестве теста я не рассматриваю. Алгоритм я пилил специально для графа, который имеет структуру, которая изображена на рисунке 3. Как поведет мой алгоритм на вашем тесте - не знаю, возможно он и не найдет путь. Тут согласен.
Похоже вы с этой проблемой уже в разработаке столкнулись и именно в попытке ее решить и воткнули этот костыль с особым рассмотрением isGoal вершины. Но это не решает проблемы. В итоге у вас получилось что-то вроде гибрида дейкстры и обхода в ширину и на некоторых тестах оно даже работает.
Да, я столкнулся именно в процессе разработки. Но я бы не назвал это костылем))
А именно, когда я рассматривал граф, изображенный на рисунке 2, тогда мой алгоритм останавливался, так и не рассмотрев вершины E и F. Поэтому мне пришлось его доработать чтобы он "перебирал" все вершины.
Значит находит не кратчайший маршрут, потому что кратчайший маршрут может идти не только по границам сетки и диагоналям в квадратах.
А я и не говорил, что это кратчайший, там написано, что это оптимальный маршрут) В случае сложной поверхности алгоритм находит именно оптимальный маршрут с использованием параметра MaxSlope. Хотя тут конечно, стоит еще проводить много экспериментов.
Не надо так болезненно реагировать на критику и пытаться всякие "сперва-добейся" применять. Я с медалями с чемпионатов мира про программированию и далеко не только Дейкстру реализовывал столько раз, сколько вы программ в своей жизни не написали.
Я не реагирую болезненно, просто не понравилось выражение "верю". Насчет медалей и побед - не знаю. Возможно это и правда.

wataru
16.11.2022 19:32+3Такие графы, которые вы привели в качестве теста я не рассматриваю.
В смысле, не рассматроиваете? Вы же там в конце еще и на 3d поверхности показываете ваш алгоритм. Вроде как с зявкой, что и на них маршрут строится. Вот я привел 3d поверхность, на ней не работает.
Ну ладно, хорошо, вот вам другой тест:

Показаны только вершины-непрепятствия. Там 4 строки. Все возможные переходы нарисованы.
Та же самая проблема. Вы найдете путь 12sqrt(2)+1=17.97 по верху, когда как кратчайший путь будет 13+2sqrt(2) =15.82 понизу.
Тут все вершины на одной z-координате. Тоже такой тест не рассматриваете?
Поэтому мне пришлось его доработать чтобы он "перебирал" все вершины.
И вы "доработали" алгоритм не правильно. Вы изначально фигню реализовали, воткнули костыль, оно все-равно не работает. Вы хоть читали-то статью на википедии, куда ссылку в самом начале дали? Вот посмотрите на нее внимательно, потом на ваш алгоритм и найдите пару отличий (обработка isGoal отдельнго — одно из них).
Второе — вам надо, как в википедии написано, вместо того чтобы проходится по списку visited вершин и у них брать соседей, вам надо среди всех вершин, которые пока не visited найти минимальную. Ее взять в качестве current и у всех соседей обновить расстояния. Вообще функций GetValidNeighbors и HasValidAndNotGoalNeighbors в корректной реализации алгоритма дейкстры быть не должно.
А я и не говорил, что это кратчайший, там написано, что это оптимальный маршрут
В смысле, оптимальный, но не кратчайший? Оптимальный по какому параметру?
просто не понравилось выражение "верю".
Ну я же вижу, что написаный вами алгоритм на алгоритм Дейкстры лишь внешне похож. Поскольку запускать ваш код лень, да у меня и среды разработки под этот язык нет, поэтому пришлось говорить так.

Green21 Автор
16.11.2022 19:52-1В смысле, не рассматроиваете? Вы же там в конце еще и на 3d поверхности показываете ваш алгоритм. Вроде как с зявкой, что и на них маршрут строится. Вот я привел 3d поверхность, на ней не работает.
3D поверхность должна превратиться вот в такой граф, с такой структурой:
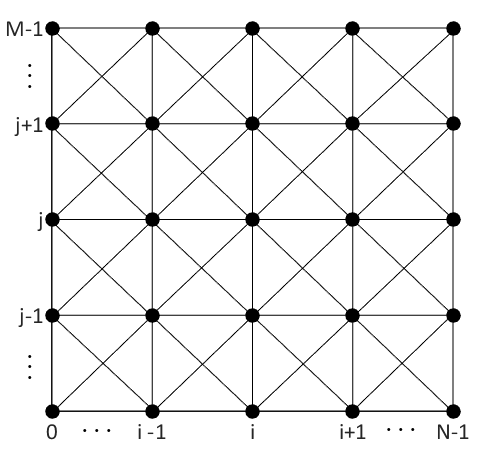
И только на графе с такой структурой мой алгоритм и работает.
На вот таком графе:
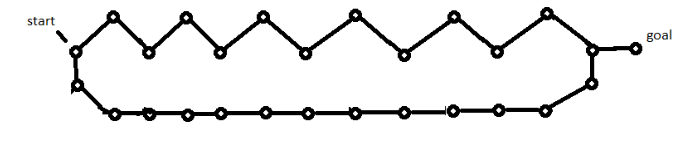
мой алгоритм не заработает. Все верно.

spovst
16.11.2022 19:59+3Т.е. ваш алгоритм работает только на одном конкретном графе, но не в общем случае? А какую ценность он вообще тогда представляет (такую, что про это стоило написать статью)? Или, скажем так, почему он представляет ценность большую, чем полноценный алгоритм Дейкстры?
Если у читателя внезапно не такой же граф, как у вас, зачем ему может понадобиться ваш алгоритм?

Green21 Автор
16.11.2022 20:15Алгоритм работает на графах, которые имеют структуру как на рисунке 3. И изначально алгоритм предназначался для поиска оптимального пути на 3D поверхности которую можно превратить в граф с такой структурой.

Green21 Автор
16.11.2022 20:16-1Если у читателя внезапно не такой же граф, как у вас, зачем ему может понадобиться ваш алгоритм?
Читатель проходит мимо и ищет подходящую реализацию или реализовывает алгоритм сам))

wataru
16.11.2022 20:10+1И только на графе с такой структурой мой алгоритм и работает.
Но приведенные мной примеры как раз такой структурой и обладают.
В точности. Просто некоторые вершины — препятствия (в этом тесте), или координаты z у них меняются. Вы же работаете с препятствиями?Вот пометки о препятствиях в примере выше (1- нельзя ходить):
{ {1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1}, {0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0}, {0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1}, {1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1} }``` Начало - вершина (1, 0). Конец - (1, 13).
Green21 Автор
16.11.2022 20:57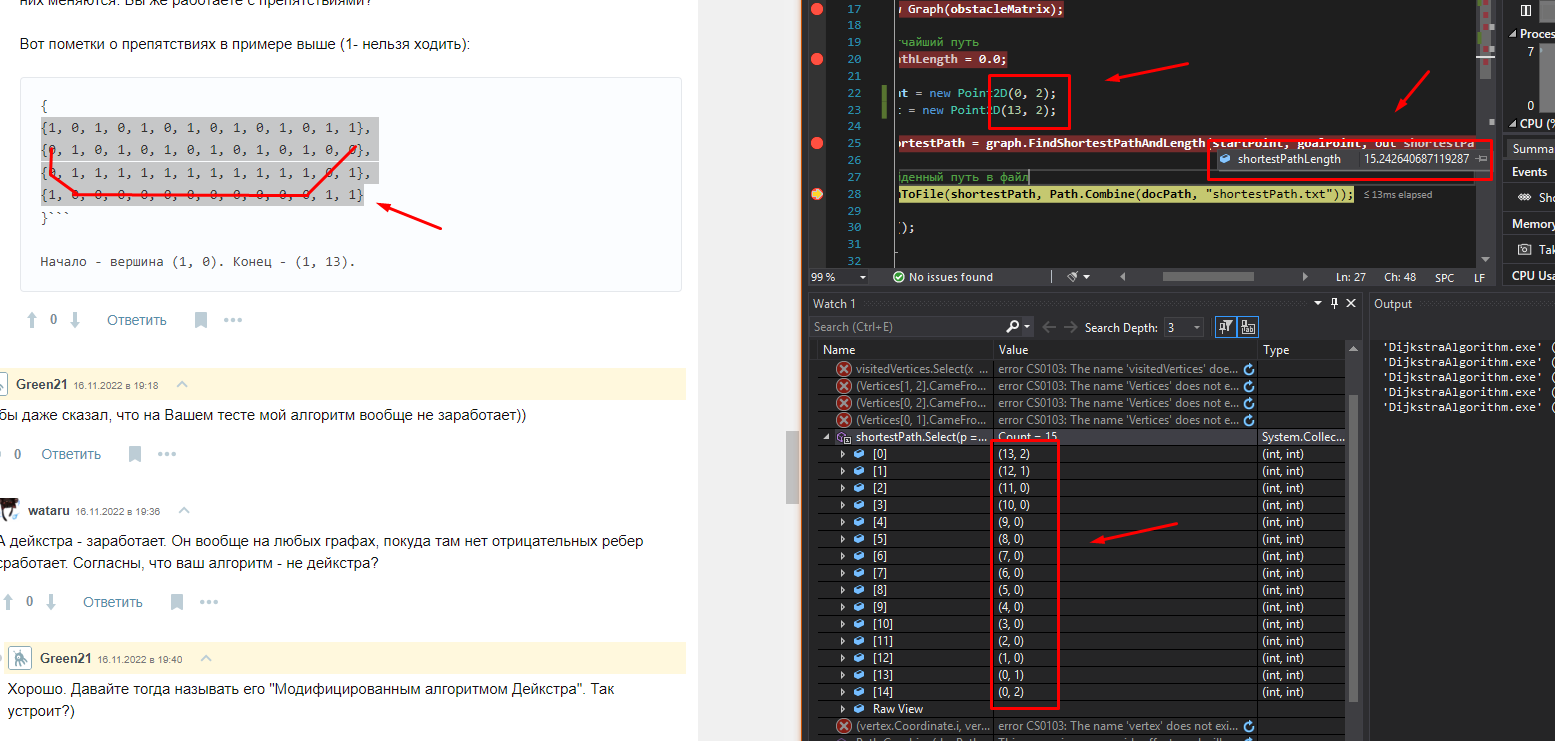
Ну вот кратчайший путь. По низу, как Вы и хотели)))))

Green21 Автор
16.11.2022 20:58Причем я не "мухливал". Запустил все как есть. Клонируйте проект, создайте файл csv с ноликами и единичками и проверьте сами.

wataru
16.11.2022 21:07Ладно, не поленился, качаю дотнет. Где там в коде задается тест?

Green21 Автор
16.11.2022 21:12Я создал отдельную ветку для тестирования прохождения препятствий. Перейдите на нее
git checkout obstacle_graph_initializing_branch

Green21 Автор
16.11.2022 21:18В файле Program.cs есть метод Main() где все задается. Вот как я задавал параметры для Вашего кейса. Только внимательно с заданием координат стартовой и целевой вершины. Вот как я задавал их для вашего примера:


wataru
16.11.2022 21:27А задайте вот такую матрицу. Надо было тест чуть увеличить:
1;0;1;0;1;0;1;0;1;0;1;0;1;0;1;0;1;0;1;0;1;0;1;0;1;0;1;0 0;1;0;1;0;1;0;1;0;1;0;1;0;1;0;1;0;1;0;1;0;1;0;1;0;1;0;1 0;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;0;1 0;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;0;1 0;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;1;0;1 1;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;1;1Вот такие вершины:
Point2D startPoint = new Point2D(0, 4); Point2D goalPoint = new Point2D(27, 5);Найдет путь по верху.
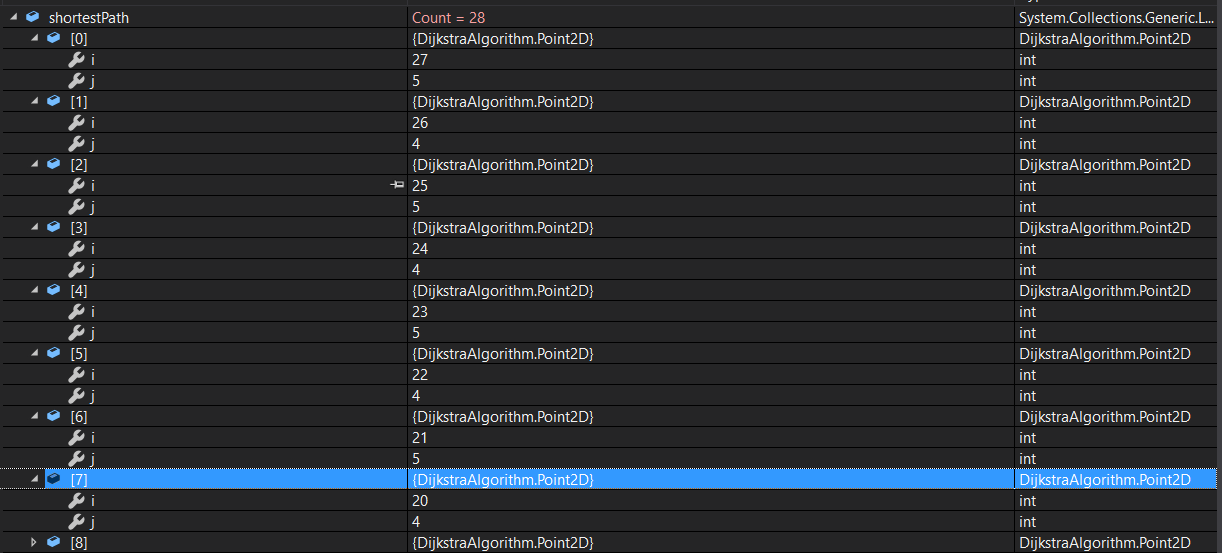
Он имеет длину 38.18. Путь понизу будет 34.24 (Можете в первой строке csv файла поставить 1 вместо какого-то нуля, чтобы найденный путь запретить и посмотреть, что программа стала выдавать путь короче).
Тест особенен тем, что самый короткий путь имеет больше шагов, чем альтернативный. Чтобы так было, путь сверху я делаю из более длинных ребер зиг-загом.

Green21 Автор
16.11.2022 19:18Я бы даже сказал, что на Вашем тесте мой алгоритм вообще не заработает))

wataru
16.11.2022 19:36А дейкстра - заработает. Он вообще на любых графах, покуда там нет отрицательных ребер сработает. Согласны, что ваш алгоритм - не дейкстра?

Green21 Автор
16.11.2022 19:40Хорошо. Давайте тогда называть его "Модифицированным алгоритмом Дейкстра". Так устроит?)

wataru
16.11.2022 20:05Нет, "Модифицированный алгоритм дейкстры" должен 1) работать во всех графах какого-то класса, 2) должен быть в чем-то лучше/проще дейкстры, пусть даже если он при этом не работает на графах вне этого класса 3) должен быть основан на алгоритме дейкстры.
У вас же алгоритм не работает на некоторых лабиринтах (я привел два примера), более сложен по реализации и медленнен по времени работы чем дейкстра, и при этом основная логика хоть и чуть-чуть похожа на дейкстру — из-за ошибки в реализации вообще другой класс алгоритма получился. Это у вас какой-то хитрый обход в ширину получился, а не дейкстра.
Назовите его "некоторая кривая реализация дейкстры, которая иногда работает".

spovst
16.11.2022 18:49+1Глобальность в том, что даже если нам будет необходимо найти кратчайший путь между двумя смежными вершинами графа, в котором 1000 вершин, нам так или иначе придется перебрать абсолютно все 1000 вершин.
Признаться, этот тезис обескураживает. И человеку, который решит начать знакомство с темой с данной статьи, от него может поплохеть и он может даже отказаться от всей затеи.
Потому что на самом деле поиск алгоритмом Дейкстры прекращается в тот момент, когда выполняется одно из двух:
перебраны все вершины и маршрут так и не найден (это означает, что маршрута не существует, и проверка этого условия, особенно на больших графах, по-хорошему должна делаться заранее, например, на базе проверки, входят ли начальная и конечная точки в одну компоненту связности);
или маршрут уже был найден и вес очередного извлечённого из очереди (да-да, для целей быстрого получения кандидата с минимальным весом следует использовать очередь с приоритетами, а не список, в котором каждый раз искать минимум, как в вашей реализации) кандидата больше, чем вес найденного маршрута (а значит, и веса всех остальных кандидатов также больше, что гарантируется свойствами очереди с приоритетами).
Ваш тезис верен только в случае, когда алгоритм Дейкстры применяется для поиска расстояний от заданной вершины до всех остальных вершин графа, но ведь это не ваш случай, вы-то ищите маршрут между конкретной парой вершин, а для этих целей следует использовать описанный мной подход с условием завершения.

Green21 Автор
16.11.2022 19:22Не совсем Вас понимаю. Я же привел пример на рисунке 2 где ясно показал, что даже для поиска кратчайшего пути между смежными (соседними) вершинами A и D нам так или иначе придется рассматривать и другие вершины графа. Вот это я и имел ввиду. Больше ничего.

spovst
16.11.2022 19:36Другие != Все. Вы берете граф из 6 вершин с определенным весами перехода и на его примере "доказываете" тезис о том, что алгоритм должен рассмотреть все вершины графа. Но достаточно поменять в нём веса, и рассматривать все вершины уже не придется.

bfDeveloper
16.11.2022 19:18Статья уровня студенческой лабораторной работы. Само по себе это не плохо, это полезно для развития. Но как можно было написать про поиск пути на сетке, не упомянув алгоритмическоую сложность, не упоминув кучу или другие способы хранения вершин, не сделав тесты производительности, не сравнив с другими алгоритмами? При том что эта задача чаще решается каким-нибудь A*, который за счёт эвристики значительно быстрее.

wataru
16.11.2022 19:33Да ладно, про неполноту. Алгоритм вообще не правильно реализован.

Green21 Автор
16.11.2022 19:37С Вашего позволения, я больше не хочу с Вами спорить)
Был бы он не правильно реализован - он бы не нашел те маршруты, которые я привел на рисунках.

wataru
16.11.2022 20:12Неправильный алгоритм неправилен тем, что он работает не всегда. Не на всех допустимых входных данных. Так, например
write("1 2 3 4 5")— неправильная реализация алгоритма быстрой сортировки. Хоть он и сортирует массив {5,4,3,2,1} или {1,3,2,4,5}.












gdQuel
Часть про 3d была полезной, спасибо