Умный в гору не пойдет / forpes.ru

Главная
Умный в гору не пойдет

Умный в гору не пойдет +18

28.09.2022 21:47

Green21 20 5900 Источник

Доброго дня, хабровчане!

Поделюсь с Вами одним численным алгоритмом вычислительной математики для построения оптимального пути движения на сложной поверхности. Под оптимальностью понимается построение такого маршрута, который проходит по карте местности, огибая все локальные экстремумы (возвышенности и впадины), обеспечивая таким образом некоторую степень минимизации перепада высот и длину всего маршрута.

Входная поверхность задана множеством точек (облаком точек) в трехмерном евклидовом пространстве и имитирует собой ландшафт со всеми его неровностями: возвышенности, холмы, горы, овраги, впадины, разломы и т.д. В качестве начального условия выбирается любая точка на поверхности.

Задачу можно рассматривать как продолжение уже имеющегося маршрута. Куда в конце концов упрется наш искомый путь нам неважно, — главное ~~начать, а там как пойдет~~, чтобы он обогнул неровности. Алгоритм также не гарантирует прохождения маршрута через какие-либо заранее заданные точки из входного множества точек. Гладкость входной поверхности сильно влияет на гладкость и адекватность получаемого решения.

Алгоритм имеет эвристическую природу, поэтому в данной статье не приводятся строгие математические доказательства существования и единственности найденного решения.

Постановка задачи

В декартовой прямоугольной системе координат на плоскости задана равномерная сетка:

$\{ x_i = i \cdot \Delta x, \ \ i = 0, \ldots, N \} \\ \{ y_j = j \cdot \Delta y,\ \ j = 0, \ldots, M \}$

где — узлы сетки; $\Delta x, \Delta y$ — шаги сеток по осии, соответственно. В каждом узле сетки задано значение $z_{i, j} = z (x_i, y_j)$ , представляющее собой высоту карты (ландшафта) местности в рассматриваемой точке. Значения $z_{i, j}$ , образующие исследуемую поверхность, могут быть отрицательными — в таком случае высоту карты следует понимать как глубину относительно некоторой нулевой отметки .

В качестве начального условия задана точка $\overline{z}=z(x_{\,\overline{N}}, y_{\,\overline{M}})$ , которая может представлять собой крайнюю точку уже известного маршрута. Его необходимо продолжить далее через всю карту к плоскости , рисунок 1.

Рисунок 1. Пример ландшафта местности — исследуемая поверхность, заданная множеством точек. Синим цветом отмечена часть известного маршрута. Красная точка — начальное условие, точка из которой необходимо продолжить маршрут.

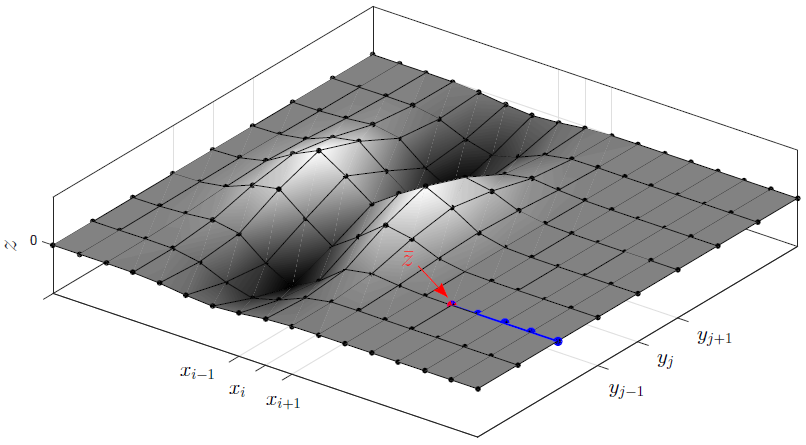
Численный алгоритм

Рассмотрим три ближайшие к $\overline{z}$ соседние точки поверхности — , находящиеся на соседнем слое по оси . Одна из этих точек лежит на том же слое по оси , что и $\overline{z}$ , а остальные лежат по диагонали к точке $\overline{z}$ , рисунок 2.

Рисунок 2. Соседние точки по оси Ox для начального условия.

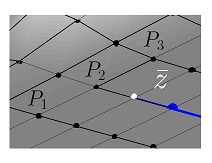
Вычислительный алгоритм построения оптимального маршрута является итерационным. На каждой итерации из трех соседних точек необходимо найти такую, сумма квадрата расстояния и квадрата тангенса угла наклона к которой является минимальной.

Для упрощения выкладок введем следующие обозначения:

$d(\overline{z}, P_k)$ — расстояние от точки $\overline{z}$ до точки ;

$\tan(\overline{z}, P_k)$ — тангенс угла, одна сторона которого — это отрезок, соединяющий $\overline{z}$ и, а другая сторона — отрезок, соединяющий $\overline{z}$ и основание перпендикуляра, опущенного из точки на плоскость перпендикулярную оси и проходящую через точку $\overline{z}$ (углы $\alpha_1, \alpha_2, \alpha_3$ , рисунок 3).

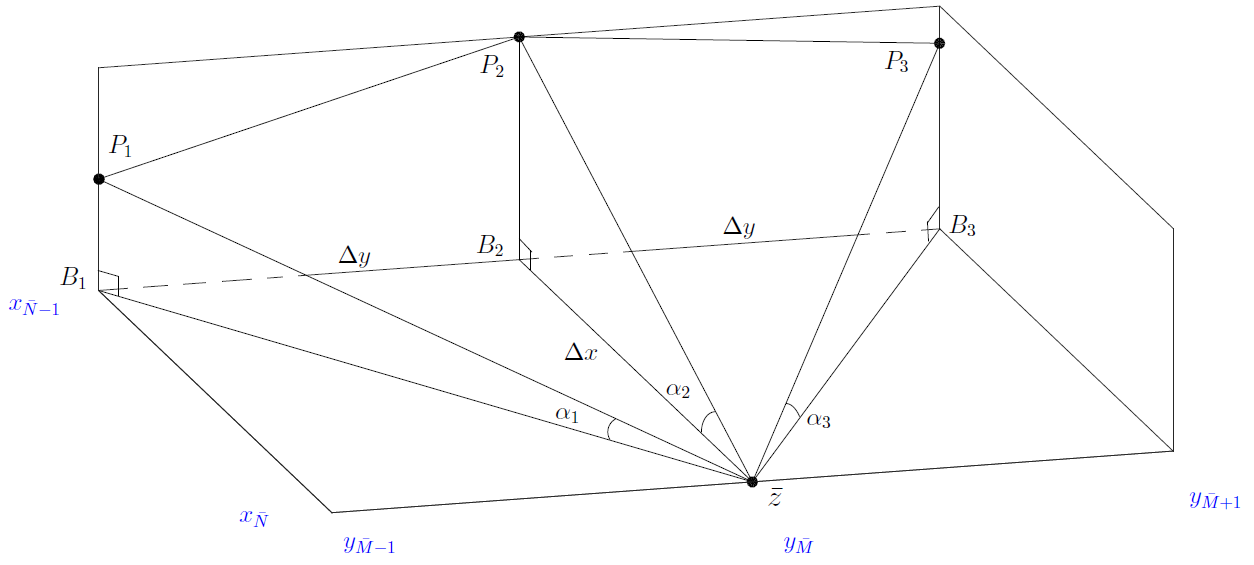
Рисунок 3. Схематический чертеж исследуемого множества точек. Начало искомого пути z, который необходимо продолжить и три соседние точки поверхности — P_1, P_2, P_3, из которых нужно будет вы-
брать одну, удовлетворяющую условию минимизации. Точки B_k — это основания перпендикуляров, опущенных из точек P_k — Рисунок 3. Схематический чертеж исследуемого множества точек. Начало искомого пути z, который необходимо продолжить и три соседние точки поверхности — P_1, P_2, P_3, из которых нужно будет вы- брать одну, удовлетворяющую условию минимизации. Точки B_k — это основания перпендикуляров, опущенных из точек P_k

Таким образом, в данных обозначениях смысл вышеописанного алгоритма в следующем: используя начальное условие — последнюю точку известного маршрута, $\overline{z}$ , нам необходимо найти такую точку , чтобы выполнялось условие минимизации:

$\min_{k=1, 2, 3}\left(d^2(\overline{z}, P_k) + \tan^2(\overline{z}, P_k) \right) \tag1$

После нахождения данной точки необходимо принять ее в качестве начального условия для следующей итерации. В результате на каждой итерации мы будем получать новые точки искомого оптимального пути.

Смысл слагаемых в (1) следующий: первое слагаемое отвечает за выбор точки с наименьшим расстоянием до предыдущей, и, как следствие, для минимизации суммарной длины полученного маршрута; второе слагаемое в виде квадрата тангенса необходимо для минимизации перепада высот. Таким образом, вышеописанный алгоритм будет прокладывать маршрут, стараясь обходить все локальные экстремумы, что мы и увидим в
экспериментах. Вместо тангенса можно было бы с тем же успехом использовать синус, что никак не повлияет на результат работы алгоритма.

В процессе расчетов может оказаться, что точка $\overline{z}$ будет находиться на крайнем слое по оси (или ) — в таком случае необходимо рассматривать не три соседние точки , а две — одна из которых лежит "по прямой", а другая "по диагонали" к точке $\overline{z}$ , при этом алгоритм построения оптимального маршрута никак не изменится.

Сложность алгоритма составляет $\approx O(3n)$ и зависит от "длины" карты, на которой необходимо проложить искомый маршрут. На каждой итерации необходимо проверять по 2-3 точки и находить минимальное значение (1).

Реализация алгоритма

Исходники находятся здесь

Определим свой класс для точки в пространстве:

class Point3D:
    def __init__(self, N, M, z, PositionalParameter):
        self.N = N
        self.M = M
        self.z = z
        self.PositionalParameter = PositionalParameter

Для удобства вместо и я использовал и , соответственно. PositionalParameter будет равен единице для точек и нулю для точки дабы немного упростить вычисления квадратов, упомянутых в формуле (1).

Определим функцию для подсчета квадрата расстояния:

def GetSquareOfDistance(point, testedPoint, dy):
    """Возвращает относительный квадрат расстояния до проверяемой точки"""
    return math.pow(point.z - testedPoint.z, 2.0) + testedPoint.PositionalParameter * dy * dy

point — это точка $\overline{z}$ , testedPoint — точка , — шаг по оси .

На самом деле здесь не совсем квадрат расстояния, а немного упрощенное значение, которое не учитывает шаг $\Delta x$ , т.к. для поиска минимального значения в (1) его можно выкинуть (предоставлю читателю возможность это проверить).

А также функцию для подсчета квадрата тангенса:

def GetTangentSquare(point, testedPoint, dx, dy):
    """Возвращает квадрат тангенса угла между точками"""
    return math.pow(point.z - testedPoint.z, 2.0) / (dx * dx + testedPoint.PositionalParameter * dy * dy)

В отдельном файле были определены функции для формирования поверхностей как функции двух переменных:

import math

# Возвращает сумму квадрата синуса первого аргумента и квадрата косинуса второго аргумента
# x - первый аргумент
# y - второй аргумент
def SinSquarePlusCosSquare(x, y):
    return math.sin(x) * math.sin(x) + math.cos(y) * math.cos(y)

# Функция Гаусса (двумерная гауссиана). 
# Описание параметров (раздел "Многомерные обобщения"): https://ru.wikipedia.org/wiki/%D0%93%D0%B0%D1%83%D1%81%D1%81%D0%BE%D0%B2%D0%B0_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F
# x, y              - точка плоскости, в которой необходимо вычислить Гауссиан
# A                 - высота колокола
# sigmaX, sigmaY    - размах колокола по оси Ox и Oy, соответственно
# x0                - сдвиг пика по оси Ox
# y0                - сдвиг пика по оси Oy
def Gaussian(x, y, A, sigmaX, sigmaY, x0, y0):
    xx = (x - x0) * (x - x0) / (2.0 * math.pow(sigmaX, 2.0))
    yy = (y - y0) * (y - y0) / (2.0 * math.pow(sigmaY, 2.0))
    return A * math.exp(-(xx + yy))

Гауссиан отлично подходит для имитации отдельно стоящей горы. А с помощью композиции можно создавать горные цепи разной длины и сложности. SinSquarePlusCosSquare создает, как Вы уже догадались, подобие холмистого рельефа.

В конце расчета маршрут записывается в файл как массив трехмерных точек.

Результаты численного решения

На следующих рисунках показаны результаты численных экспериментов нахождения оптимальных маршрутов. Для имитации ландшафта местности использовались различные аналитические поверхности. Все размерности даны в условных единицах, шаг сеток во всех расчетах по обеим осям был взят равным $\Delta x =\Delta y = 0.1$

В качестве имитации горы использовалась функция Гаусса.

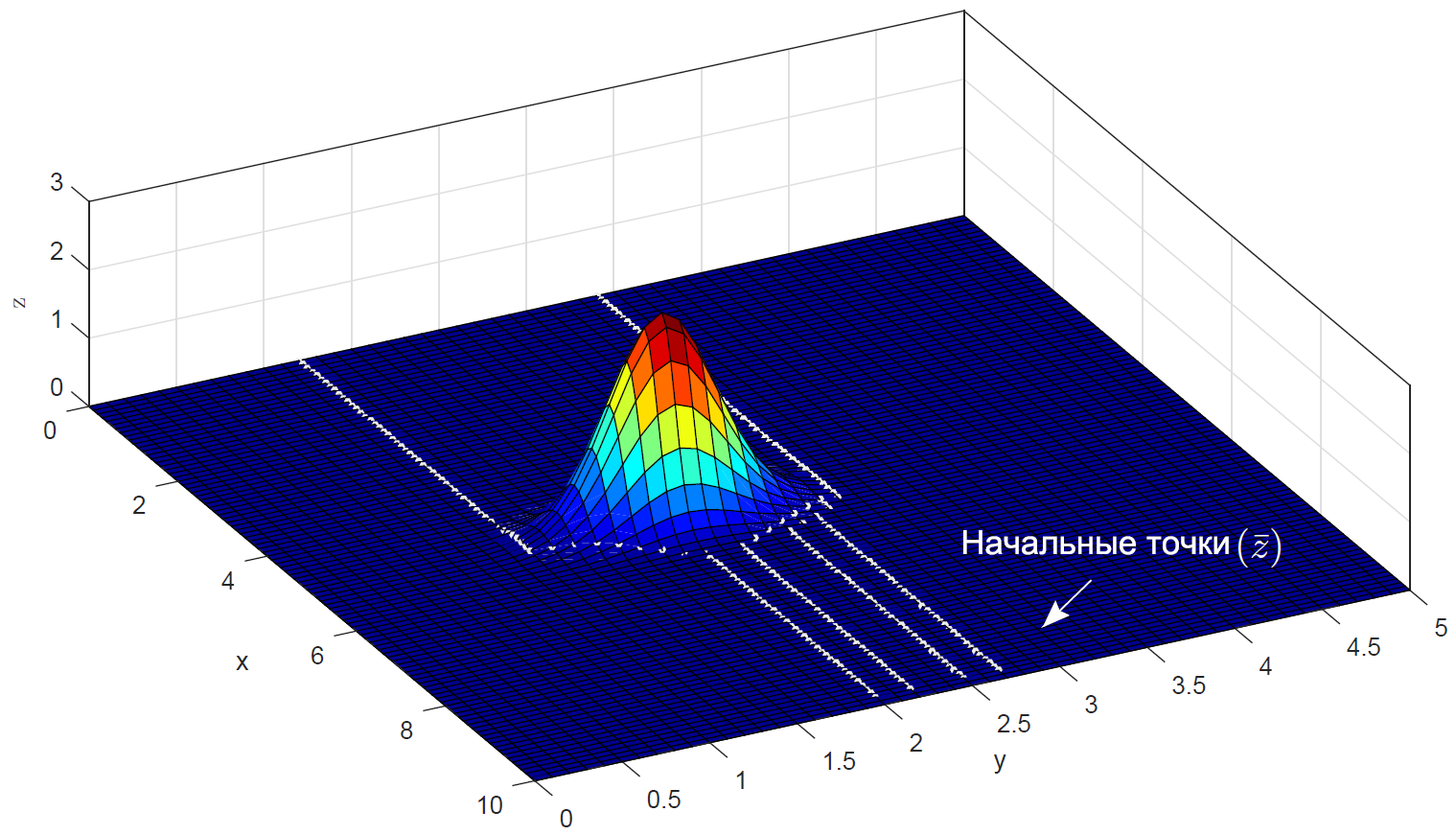
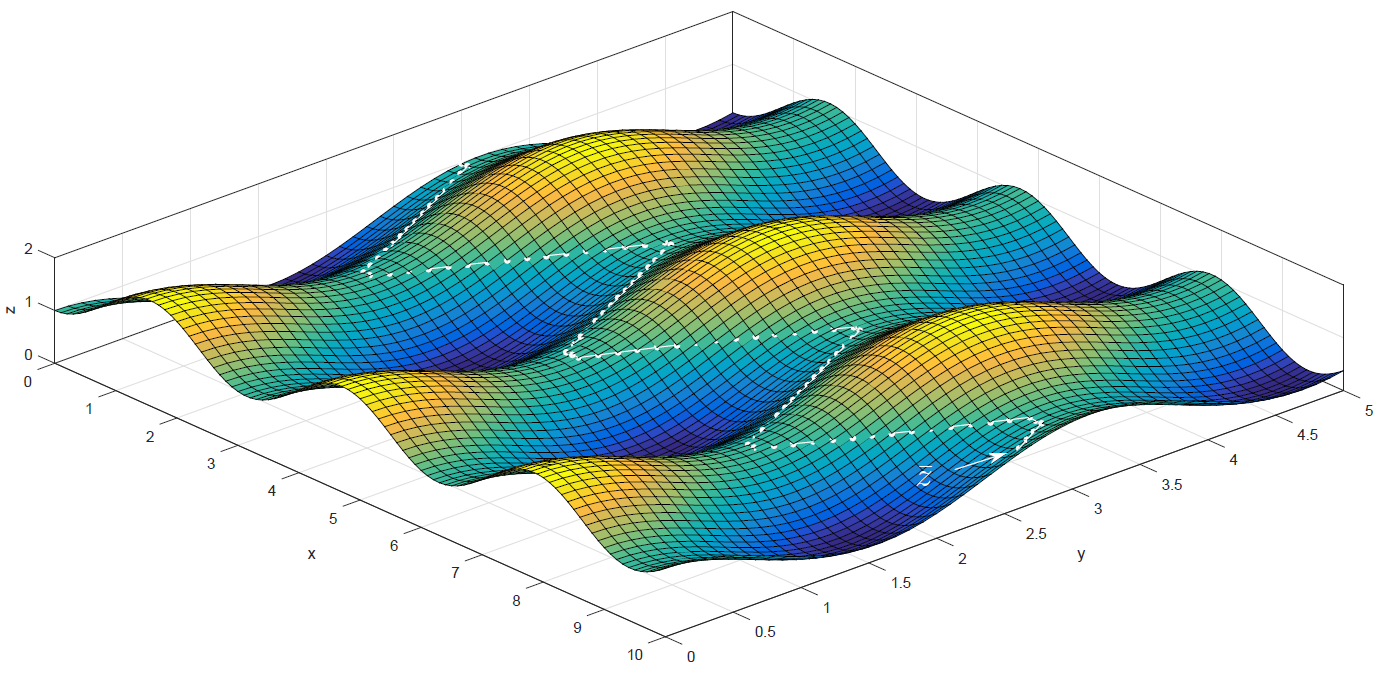
Холмистый рельеф. Имитация с помощью функции $z(x, y)= \sin^2(x)+\cos^2(y)$

Имитация холмистого ландшафта. Хорошо видно как маршрут (белая линия) обходит локальные экстремумы.

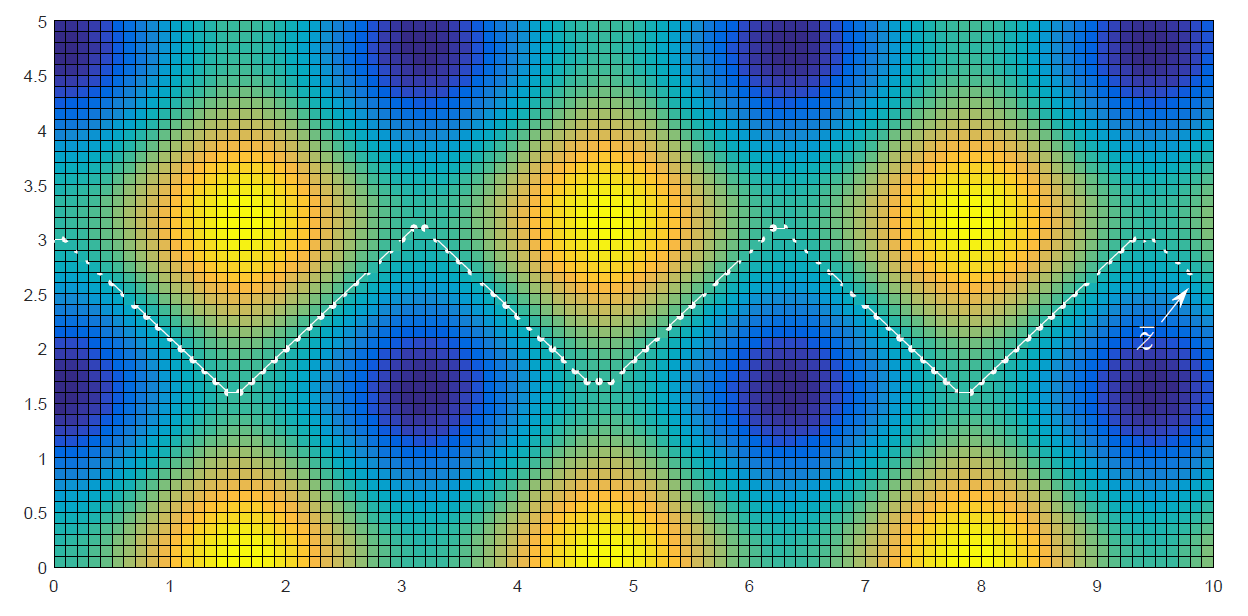
а это вид сверху:

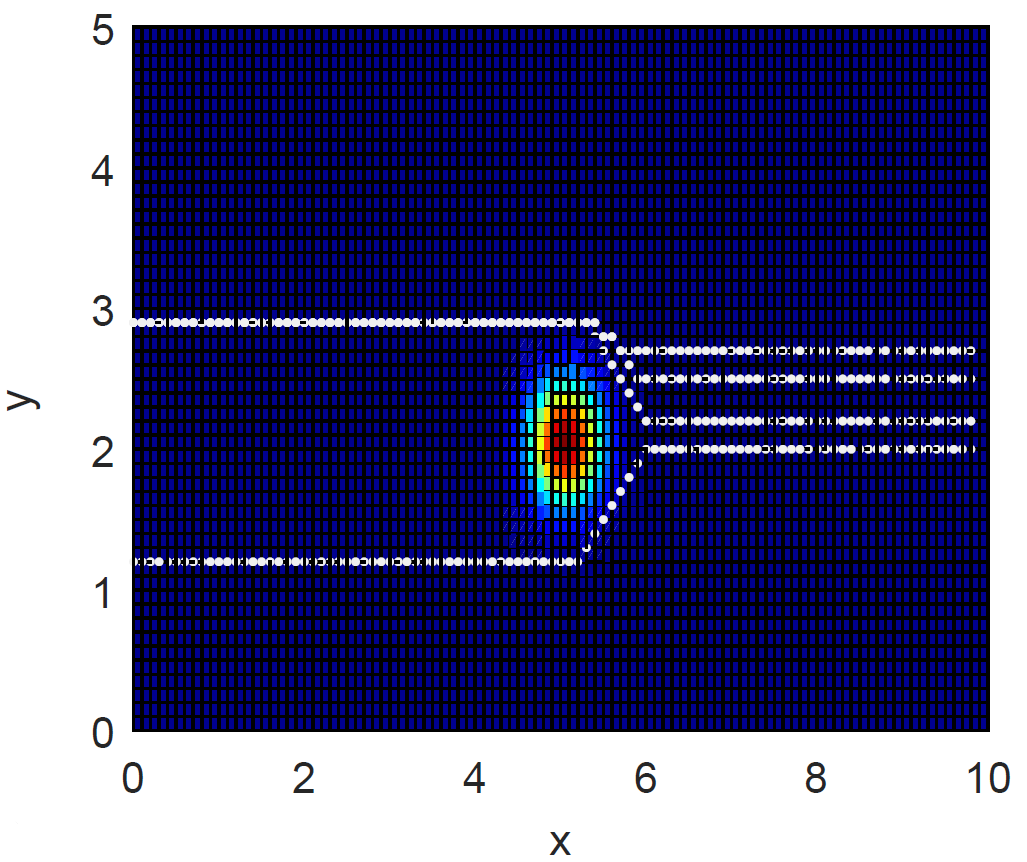
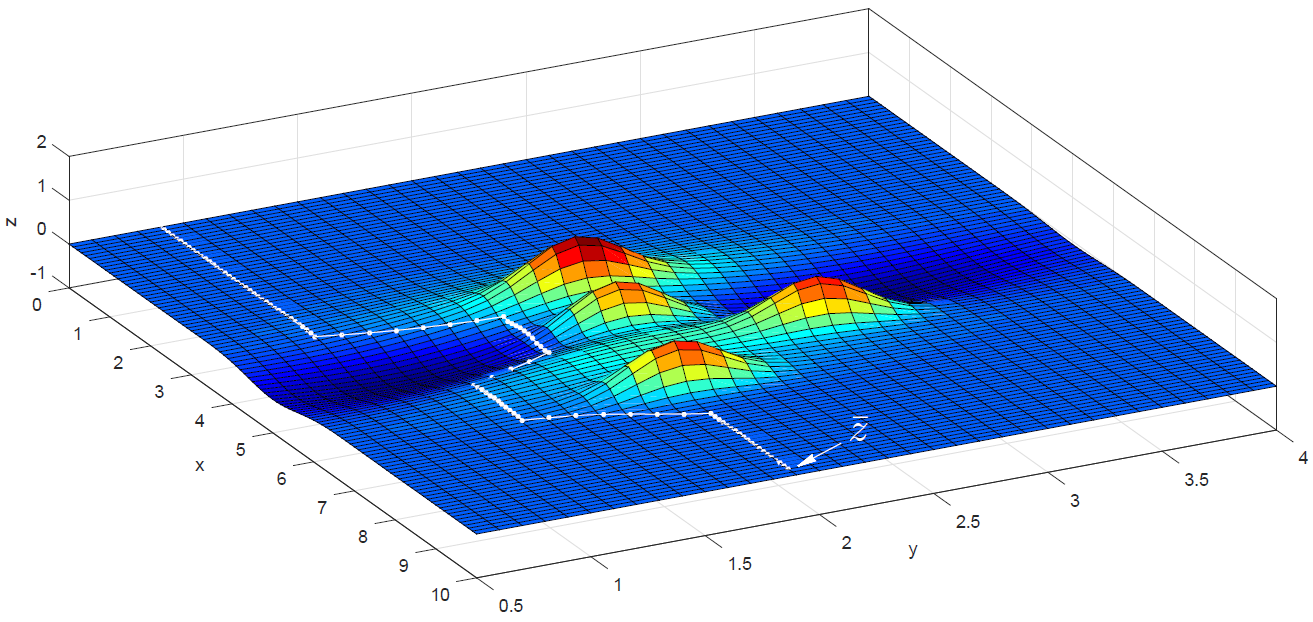
Вот еще один интересный вариант ландшафта. Наложение нескольких функций Гаусса и поверхности заданной формулой $z(x, y)=(x^2-y^2)e^{(-x^2-y^2)}$ :

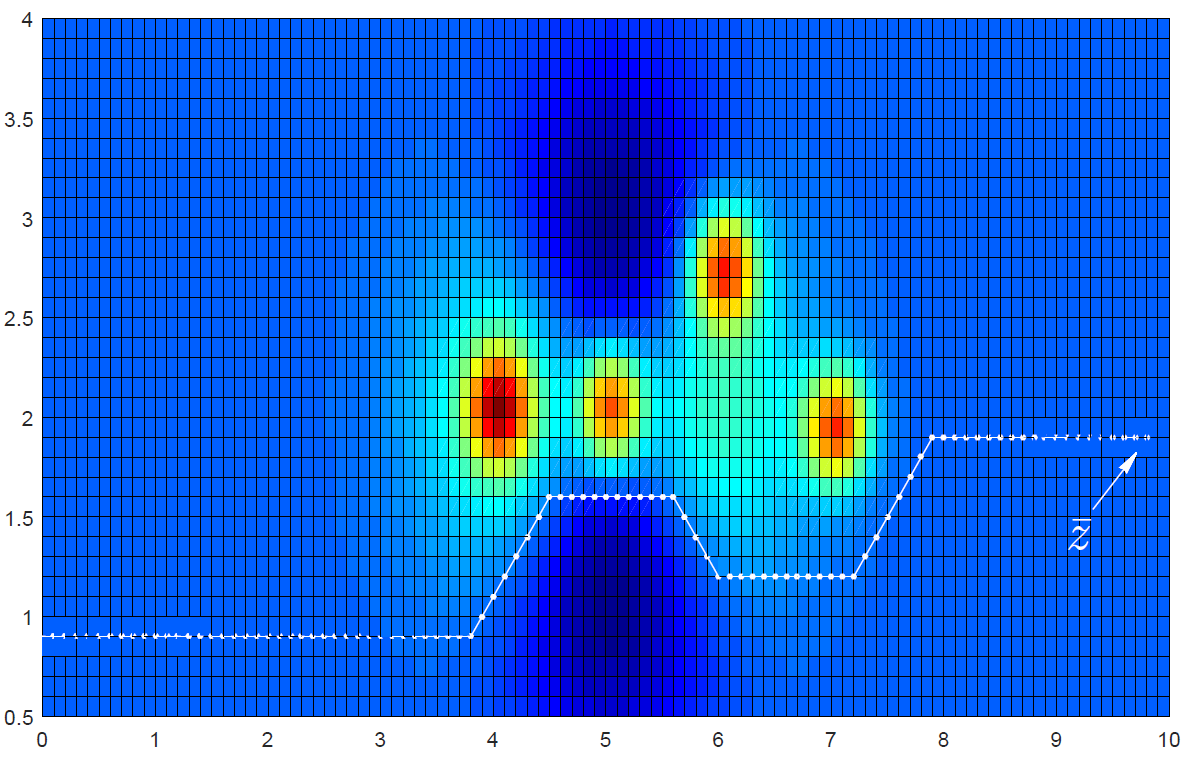
Спасибо за прочтение!

Все доработки и усовершенствования оставляю Вам.

Комментарии (20)

abutorin
28.09.2022 22:01
#24774734
+6
что-то мне подсказывает что вы изобрели градиентный спуск. )
1. Green21 Автор
  28.09.2022 22:13
  #24774750
  +1
  Ну тогда бы мы спустились в ямку и не выходили оттуда, а тут немного другое))
  1. abutorin
    28.09.2022 22:18
    #24774766
    +7
    Ну это все вопрос выбора целевой функции. Как я понял вам главное поменьше подниматься и опускаться, тогда вы можете просто взять значения целевой функции по модулю.

NumLock
28.09.2022 22:26
#24774776
+7
Эх молодежь :)
Алгоритм Ли Вам в помощь.

lorc
28.09.2022 23:07
#24774818
+12
Превращаем вашу поверхность во взвешенный граф и запускаем на нем алгоритм Дейкстры. Это даст оптимальный маршрут.

Можно попробовать расширить алгоритм Ли или алгоритм А* на случай взвешенного графа, но не знаю что получится. Возможно - что-то интересное.
1. thevlad
  29.09.2022 01:19
  #24774948
  +1
  Да тут вообще не понятно, какие цели у автора. Если исходить из того, что ему надо найти путь до правой границы, и это должен быть локальный алгоритм (подыграем по максимому и предположим так надо). Ну посчитай ты локальный гессиан, найди локальный кратчайший путь до правой границы(наверное можно даже аналитически), будет хотя бы красиво, а не вот это уперся в стенку - повернул. Да и совсем тривиальный алгоритм должен взлететь, считаем градиент, проекция вектора направления на него является оптимальной линейной аппроксимацией локального поведения функции, считаем проекцию для точек кандидатов, выбираем минимум.
  
  PS: совсем хорошая идея, локально находить при помощи МНК наилучшую плоскость, и выбирать на ней минимальный путь до правого края. На таком даже можно наверное диплом сделать, если расписать все это в виде научно-математической лабуды. )
  1. Green21 Автор
    29.09.2022 04:32
    #24775014
    По хорошему, несомненно, нужно бы находить оптимальный путь между 2-мя произвольными точками на карте. А здесь, конечно, я упростил задачу, т.к. нужно было быстро состряпать более-менее работающий алгоритм для участия в одном хакатоне, а времени для экспериментов не было )
    
    thevlad
    29.09.2022 12:07
    #24776122
    +1
    Тогда еще хуже, отличный для этого случая глобальный алгоритм - Дейкстры, или его реализация на регулярной сетки - волновой, гуглится вместе с реализацией за 15 минут. ) Надо только придумать функцию преобразования высоты в стоимость.
1. FunnyBlort
  29.09.2022 11:24
  #24775974
  +1
  Вот вот я тоже подумал - A* в студию и все будет быстро. В добавок - в A* и djskra можно вообще выбрасывать непроходимые сегменты (например если угол склона больше 35-40 градусов) и оно ещё быстрее все это обсчитает.
1. mostodont32
  30.09.2022 06:19
  #24778050
  По факту описанный в статье алгоритм - это и есть А* :)

tony-space
29.09.2022 00:31
#24774918
+3
Пришла в голову такая мысль.

А что если мы скрестим JPEG с вариационным исчислением?

Шаг 1. JPEG использует дискретное косинусное преобразование (DCT) для вычисления аналитической аппроксимации g(x,y) дискретной функции f(x,y), где значения обоих функций -- это яркость пикселя. Иначе говоря из матрицы пикселей f получаем функцию g из суммы косинусов. Большую часть этих косинусов можно выкинуть за ненадобностью. Хорошая новость в том, что в DCT косинусы не считаются для каждой точки сетки -- только для строк и столбцов (O(2N) вместо O(N^2)).

Шаг 2. Зная аналитически заданную поверхность g(x,y), можно аналитически посчитать кратчайший путь методом вариационного исчисления. Иначе говоря -- найти геодезическую линию на поверхности.

Интересно, что первый шаг -- это просто матричное умножение. Второй шаг чуть сложнее. Для простых кейсов -- это может и пушкой по воробьям, но предположу, что на огромных сетках, где есть плавные перепады высот, это может дать выигрыш. Пусть и ценою некоторой потерей точности. Бонусом также можно накладывать аналитические ограничения.

Это скорее мысли в слух, на случай если вам вдруг интересно станет в этом направлении покопать.
1. thevlad
  29.09.2022 01:43
  #24774964
  +1
  Это все сложно, я бы начал с того чтобы зафиттил при помоши МНК наилучшую локальную плоскость, а геодезику на ней до правого края найти тривиально. Если не хватает информации добрасываем квадратичную форму (аналог гессиана)

Celsius
29.09.2022 06:53
#24775186
+2
https://habr.com/ru/post/262181/

klvov
29.09.2022 08:45
#24775516
+1
Что-то напоминает, кажется принцип наименьшего действия. Даже с Википедией сверился, вроде так:

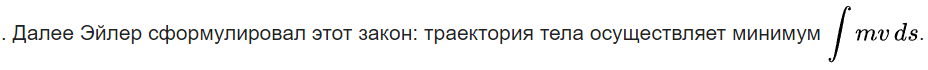
ksbes
29.09.2022 09:44
#24775630
+4
Какая-то полная хрень:

1) Складываем квадарат расстояния, метры, с квадратом тангенса, разы. Это ошибка уровня начальной школы! При изменении размерности шага одной и той же сетки роль наклона будет менятся: на мелкой (мерим в километрах) сетке алгоритм будет тупо держать начальный уровень (что мы и видим на картинках — метра хватает), а на крупной (мерим в фемтометрах) сетке — тупо переть вперёд игнорируя все перепады высот.

2) Вообще не задана задача оптимизации (если не считать, «хочу красиво»). Что оптимизируем? Длину пути? Расход энергии? Нет — ни то и не то. Какую-то странную величину не имеющую ни физических, ни математических аналогов. А раз задачи нет — то и нельзя понять правильно вы её решили или нет. Мусор на входе — мусор на выходе.

3) Тестовые примеры явно не раскрывают всех проблем алгоритма — поробуйте, например, создать «ловушку» в виде длиннной долины меж гор с тупиком — и путь у вас прекрасно пройдёт если не через локальный экстремум, то прямо рядом с ним. Да даже просто плавный холм с тангенсом наклона меньше порогового (зависит от размера шага сетки) — пройдёт прямо по экстремуму и не заметит.

Как задача на самообучение сойдёт. Но даже как алгоритм для мега тупого ИИ в игрушке, где именно такой и нужен — нет. Хотя бы потому что надо тангенсы считать, которые можно заменить просто квадратом перепада высоты с даже лучшим результатом (который не будет так сильно зависеть от шага)

maty
29.09.2022 10:50
#24775832
+1
Бросаются в глаза следующие проблемы.
(1) Точки P1,P2,P3 -- находятся строго впереди по оси Ох. Как следствие, если оптимальный путь должен будет содержать участки с движением в противоположном направлении, то алгоритм будет не в состоянии его найти. Например это может быть сильно извилистая тропинка между высоких гор.
(2) Отказаться от (1), может быть затруднительно, потому что в функция ошибки не содержит предыдущего направления движения. Для иллюстрации, можно рассмотреть плоскую поверхность (без холмов). На такой поверхности, для выбранной функции ошибки, не важно куда идти (верх, низ, вперед, назад) и, вообще говоря получится случайное блуждание. Именно искуственный выбор "всегда продвигаться вперед" и решает подобную проблема, а совсем не оптимальность направления.
(3) точки P1 и P3 дальше от точки отсчета, чем P2. Это подсказка, что нам больше нравится двигаться прямо (жесткая эвристика). При этом на плоскости эти пути должны быть равнозначны. Кроме того, это не позволяет применять алгоритм для других решеток.
(4) Почему добавлен именно tan? Видимо, просто потому что он легко вычисляется (отношения катетов, которые нам известны). Но учитывая, что шаг сетки фиксирован, можно было просто высоту брать с подборным коэффициентом.
(5) При подходящем выборе коэффициента перед tan (в функции ошибки), эта функция ошибки просто сводится к расстоянию от начальной точки до P1-P3. Учитывая, как выбраны P1-P3 (см. (1)), мы легко можем пойти в гору, а не по прямой.
(6) Контрпример. Пусть при x not= 0 высота строго равна нулю. При х=0 у нас дорожка ведущая в гору с фиксированным небольшим углом (пусть его tan^2 = a).
Для удобства будем считать DeX=DeY=1. Для направлений P1 и P3 скор равен 2, для Р2 скор равен 1 + a.
Получаем, что при a < 1 алгорим предложит нам идти в гору, хотя выгодне было немного свернуть.
Это следствие плохо выбранного скора и точек P1-P3.
1. thevlad
  29.09.2022 11:25
  #24775980
  Да жадная локальность, которая может завести в тупик, самая большая проблема. Надо либо строить карту, либо использовать глобальный алгоритм(Дейкстры, или его реализация на регулярной сетки - волновой). Если реализовать как волновой, то это будет single source shortest path tree, то достаточно пройти вдоль значений в правой границе и выбрать минимальное, это и будет оптимальный путь из точки до правой границы.

Green21 Автор
29.09.2022 16:44
#24776920
+1
Спасибо всем за конструктивные комментарии!

Судя по частоте упоминания, самым оптимальным алгоритмом является алгоритм Дейкстры. Поэтому как появится время и желание - попробую его реализовать для нахождения оптимального маршрута между двумя произвольными точками на карте и написать статью.

По хорошему, помимо естественных ландшафтов - также необходимо добавлять на карту препятствия неприродного характера - здания и др. сооружения, которые, понятное дело, не сможет обойти алгоритм, описанный в этой статье.

asrtonom4ek
30.09.2022 00:08
#24777814
+1
судя по картинкам алгоритм просто идет по изовысоте (линии равной высоты), в принципе для поставленной задачи избегать горок это лучшее решение)
1. Green21 Автор
  30.09.2022 00:20
  #24777828
  В принципе, да. Для работы этого алгоритма поверхность должна быть гладкой. Сложные препятствия из зданий, стен и т.п. обходить он не умеет.

Умный в гору не пойдет +18

Постановка задачи

Численный алгоритм

Реализация алгоритма

Результаты численного решения

Комментарии (20)

Green21 Автор

Green21 Автор

Green21 Автор

Green21 Автор