Доброго дня, хабровчане!
В этой статье поговорим о такой современной, модной и очень важной теме как машинное обучение и нейронные сети. О важности этой темы я писать не буду — каждый день об этом говорят по телевизору и пишут в газетах интернетах.
Тема распознавания цифр на основе данных от MNIST уже достаточно заезженная, но я все-таки поделюсь с Вами своим первым опытом в этой области, который привел к определенному результату, правдивость и достоверность которого Вы сможете сами проверить.
Итак, о чем же эта статья?!
В статье я буду с нуля реализовывать классический алгоритм обратного распространения ошибки с помощью последовательного (стохастического) режима обучения, чтобы обучить многослойный персептрон (полносвязную нейронную сеть прямого распространения) распознавать рукописные цифры. Каждый свой шаг я буду стараться подробно комментировать, ссылаясь на книгу Хайкина по нейросетям. Я думаю многие, кто занимается машинным обучением профессионально, начинали свой путь именно с этой книги, ну или хотя пару раз заглянули в нее.
Как Вы заметили, эта статья является переводом. Я бы сказал — частичным переводом, так как в оригинальной статье автор пишет алгоритм на языке C. Я же буду писать на C#.
К тому же, точность предсказаний обученной нейросети зависит от очень большого количества параметров: архитектура сети, количество скрытых слоев, количество нейронов на слоях, функции активации, инициализация весовых коэффициентов и т.д. Поэтому в качестве упрощения я буду идти примерно той же дорогой, как и автор оригинала для ускоренного получения более-менее приемлемого результата.
От Вас требуются элементарные знания высшей математики (знать что такое сумма от 1 до n, что такое функция и производная) ну и иметь хотя бы какое-то общее представление о нейронных сетях. Было бы неплохо прочесть первую главу Хайкина.
Содержание
Обучающая выборка. MNIST
Для тех, кто первый раз видит эту аббревиатуру. В качестве данных для обучения я использовал изображения рукописных цифр из базы данных MNIST. Скачать бинарные файлы с изображениями и метками можно здесь. Но на всякий случай я загрузил их в свой проект.
Пару слов про эти бинарники. Файлы train-images-idx3-ubyte и train-labels-idx1-ubyte содержат в себе 60К изображений и меток (наименование цифры) в закодированном виде, соответственно. Эта выборка будет служить для обучения нейросети и корректировки весовых коэффициентов. Файлы t10k-images-idx3-ubyte и t10k-labels-idx1-ubyte содержат 10К картинок и меток, соответственно, для тестирования уже обученной нейросети.
Для работы с этими файлами я использовал библиотеку MNIST.IO, которая отлично справилась со своей задачей. Хотя для тренировки нейросети это и не нужно, но мне все-таки захотелось взглянуть на эти картинки "вживую", поэтому я раскодировал все изображения и сохранил их в соответствующие папки проекта. Здесь находятся 60К из тренировочной выборки, а тут 10К для тестирования.
Каждая картинка имеет размер 28*28 пикселей и представляет из себя черно-белое изображение рукописной цифры от 0 до 9.
Результаты
Пожалуй, начну сразу с результатов. Результатом является обученный персептрон (784-80-10), т.е. нейросеть у которой 784 входа, один единственный скрытый слой с 80-ю нейронами и 10 выходных нейронов. При тестировании на выборке из 10К он показал точность распознавания % (т.е. он удачно распознал 9572 цифры из 10К), остальные 428 ему распознать не удалось. Их я решил сохранить в отдельную папку (в названии каждой картинки три числа: порядковый номер, ожидаемый ответ, ответ от нейросети). Обучал в 16 эпох (16*60К изображений) с параметров обучения =
.
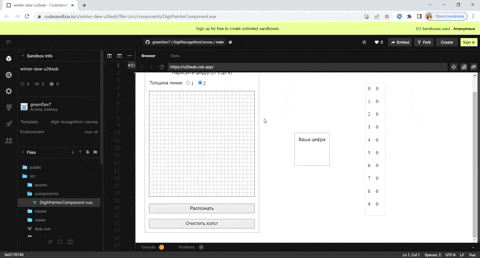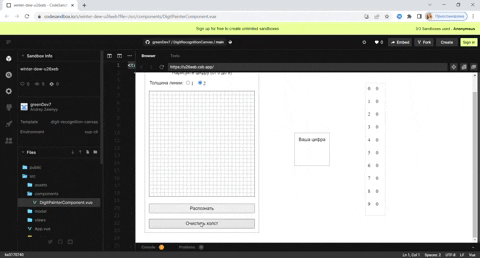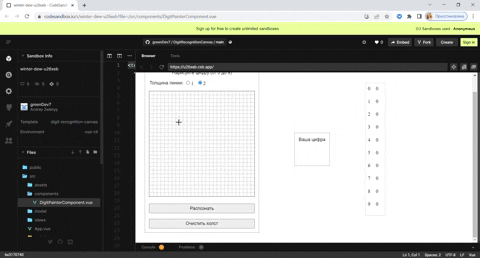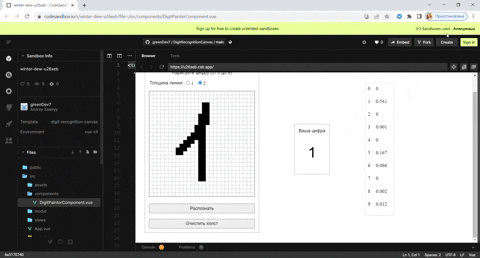
Уже готовые, скорректированные весовые коэффициенты скрытого и выходного слоя находятся здесь. Для экспериментов я создал песочницу с уже обученной моделью (на основе уже готовых коэффициентов) где на холсте размером 28 на 28 пикселей можно нарисовать свою цифру для распознавания и посмотреть на результат:
Модель нейрона
Модель нейрона в моей реализации имеет следующий вид:
public class Neuron
{
/// <summary>
/// Весовые коэффициенты (синаптические связи)
/// </summary>
public List<double> Weights { get; }
/// <summary>
/// Пороговое значение
/// </summary>
public double Bias { get; }
/// <summary>
/// Функция активации
/// </summary>
private Func<double, double> ActivationFunction { get; }
/// <summary>
/// Индуцированное локальное поле
/// </summary>
public double InducedLocalField { get; private set; }
/// <summary>
/// Локальный градиент
/// </summary>
public double LocalGradient { get; private set; }
}Везде далее, если необходимо, я буду указывать в скобочках страницу и/или формулу и номер раздела в книге Хайкина, на основе которых я строил свою модель. Модель нейрона была взята со стр. 43, п. 1.3.
Что такое Weights, Bias и ActivationFunction думаю и так понятно. Свойство InducedLocalField будет использоваться как при прямом проходе, так и в методе обратного распространения (обратный проход) для корректировки весовых коэффициентов, — поэтому задавать его я буду уже при прямом проходе сигнала через сеть, чтобы на обратном пути брать уже вычисленное значение. LocalGradient необходим лишь на обратном проходе для корректировки весовых коэффициентов. Свойство ActivationFunction имеет функциональный тип данных, чтобы можно было подставлять разные функции активации.
Все-таки пару слов о Weights сказать нужно. На самом деле неправильно утверждать, что весовые коэффициенты принадлежат какому-то конкретному нейрону. Для тех кто знаком с графами — это как вес ребра, связывающего две соседние вершины графа, так и здесь, весовой коэффициент относится к синапсу, который связывает нейрон одного слоя с нейроном (либо входом) соседнего слоя.
Но в моей модели список Weights будет относиться к синапсам, которые связывают данный нейрон и нейроны предыдущего (расположенного левее) слоя. Поэтому это свойство включено в класс нейрона.
Забегая наперед, нужно отметить, что, в таком случае, для алгоритма обратного распространения нужно реализовать отдельный метод, который будет находить список весовых коэффициентов, относящихся к синапсам, связывающих данный нейрон и нейроны следующего за ним (расположенного правее) слоя. Я думаю, это станет понятней в дальнейшем в процессе реализации.
Функции активации (и их производные) хранятся отдельно:
ActivationFunctions.cs
public static class ActivationFunctions
{
/// <summary>
/// Параметр для сигмоидальной функции активации
/// </summary>
private const double a = 1.0;
/// <summary>
/// Пороговая функция активации (использовалась для тестирования и решения проблемы XOR)
/// </summary>
/// <param name="x">аргумент функции</param>
/// <returns></returns>
public static double ThresholdFunction(double x)
{
return x >= 0.0 ? 1.0 : 0.0;
}
/// <summary>
/// Возвращает значение сигмоидальной функции активации
/// </summary>
/// <param name="x">аргумент функции</param>
/// <returns></returns>
public static double SigmoidFunction(double x)
{
return 1.0 / (1.0 + Math.Pow(Math.E, -a * x));
}
/// <summary>
/// Возвращает значение производной сигмоидальной функции активации (для алгоритма обратного распространения)
/// </summary>
/// <param name="x">аргумент функции</param>
/// <returns></returns>
public static double SigmoidFunctionsDerivative(double x)
{
double factor = a * Math.Pow(Math.E, -a * x);
return factor * Math.Pow(SigmoidFunction(x), 2.0);
}
}Модель слоя
public class Layer
{
/// <summary>
/// Нейроны
/// </summary>
public List<Neuron> Neurons { get; }
/// <summary>
/// Входной сигнал
/// </summary>
public List<double> InputSignals { get; set; }
}Состоит из свойств Neurons — список нейронов данного слоя и InputSignals — входные сигналы, полученные от предыдущего слоя. InputSignals будут также сохраняться при прямом проходе, чтобы использовать их на обратном.
Модель нейронной сети
public class Network
{
/// <summary>
/// Скрытые слои
/// </summary>
public List<Layer> HiddenLayers { get; }
/// <summary>
/// Выходной слой
/// </summary>
public Layer OutputLayer { get; }
}Модель нейросети состоит из списка скрытых HiddenLayers слоев и выходного слоя —OutputLayer.
Подготовка обучающей выборки. Архитектура сети
Для того чтобы запустить алгоритм обучения, необходимо каждый обучающий пример, а именно изображение с цифрой, преобразовать в сигнал, который будет скормлен нашему персептрону.
Каждое MNIST-изображение представляет из себя матрицу 28*28 пикселей со значениями в диапазоне от 0 до 255 (оттенок серого цвета). Но для наших целей мы поступим следующим образом — все белые пиксели (со значением 0) мы так и оставим нулем, а все остальные пиксели будем рассматривать как черный цвет, рисунок 2.
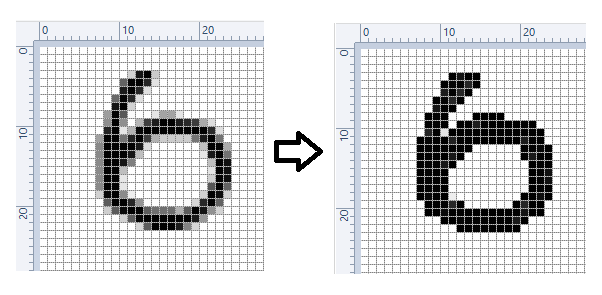
После этого мы "расслоим" наше изображение:

и из полученных слоев составим вектор входного сигнала с набором из элементов. Белые и черные пиксели, будут представлять, соответственно, 0-ки и 1-ки.
Для этих целей был создан вспомогательный метод:
ConvertImageToFunctionSignal()
public static List<double> ConvertImageToFunctionSignal(byte[,] image)
{
List<double> functionSignal = new List<double>();
for (int i = 0; i < image.GetLength(0); i++)
for (int j = 0; j < image.GetLength(1); j++)
functionSignal.Add(image[i, j] == 0 ? 0.0 : 1.0);
return functionSignal;
}Таким образом, у нас будет полносвязная нейронная сеть прямого распространения, состоящая из 784 входов, 1 скрытого слоя и выходного слоя с 10 нейронами. Все нейроны будут иметь сигмоидную функцию активации. Количество нейронов на скрытом слое будем варьировать для получения лучшего результата.
Инициализация нейросети
Как оказалось, не только необходимым, но и важным этапом в процессе обучения нейросети является инициализация ее весовых коэффициентов. Как пишет автор оригинала, нейросеть показала более высокую точность когда при ее инициализации всем весовым коэффициентам были присвоены рандомные значения от 0 до 1 с чередованием знаков. Т.е. каждый четный весовой коэффициент был положительным, а каждый нечетный — отрицательным. Тоже самое я решил применить не только к весам, но и к пороговым значениям (Bias), чтобы одна их половина была положительной, а другая — отрицательной.
А теперь — как это реализовано на практике.
В классе Network реализовано два конструктора. Один из них инициализирует всю сеть (весовые коэффициенты) рандомными значениями, а смысл другого конструктора в том, чтобы инициализировать сеть по уже скорректированным весовым коэффициентам, которые хранятся в текстовом файле.
Вот листинг кода первого конструктора с комментариями:
Network(). Конструктор для рандомной инициализации
/// <summary>
/// Инициализирует нейросеть с помощью входных параметров
/// </summary>
/// <param name="inputLayerDimension">количество входов нейросети</param>
/// <param name="outputLayerNeuronsCount">количество нейронов на выходном слое</param>
/// <param name="outputActivationFunction">функция активации у нейронов выходного слоя</param>
/// <param name="hiddenLayersDimensions">размерности скрытых слоев</param>
/// <param name="hiddenActivationFunctions">массив функций активаций нейронов скрытых слоев</param>
/// <param name="randomMinValue">левая граница для рандомных чисел</param>
/// <param name="randomMaxValue">правая граница для рандомных чисел</param>
public Network(int inputLayerDimension, int outputLayerNeuronsCount, Func<double, double> outputActivationFunction, int[] hiddenLayersDimensions = null,
Func<double, double>[] hiddenActivationFunctions = null, double randomMinValue = 0.0, double randomMaxValue = 1.0)
{
Random random = new Random();
// Если есть скрытые слои
if (hiddenLayersDimensions != null)
{
HiddenLayers = new List<Layer>();
// Сначала инициализируем первый скрытый слой
// Количество весовых коэффициентов у каждого нейрона первого скрытого слоя равно количеству нейронов входного слоя
HiddenLayers.Add(new Layer(CreateNeurons(hiddenLayersDimensions[0], inputLayerDimension, randomMinValue, randomMaxValue, hiddenActivationFunctions[0], random)));
// Если скрытых слоев больше 1
if (hiddenLayersDimensions.Length > 1)
{
// Количество весовых коэффициентов на втором и последующих скрытых слоях равно количеству нейронов на предыдущем скрытом слое
// Еще раз, первый скрытый слой уже проинициализирован, поэтому начинаем со второго (h = 1)
for (int h = 1; h < hiddenLayersDimensions.Length; h++)
HiddenLayers.Add(new Layer(CreateNeurons(hiddenLayersDimensions[h], hiddenLayersDimensions[h - 1], randomMinValue, randomMaxValue, hiddenActivationFunctions[h], random)));
}
}
// Если есть скрытые слои, то количество весовых коэффицинтов у нейронов выходного слоя равно количеству нейронов последнего скрытого слоя
// Если скрытых слоев нет, то количество весовых коэффицинтов у нейронов выходного слоя равно количеству входов сети
int outputWeightsCount = hiddenLayersDimensions != null ? hiddenLayersDimensions.Last() : inputLayerDimension;
OutputLayer = new Layer(CreateNeurons(outputLayerNeuronsCount, outputWeightsCount, randomMinValue, randomMaxValue, outputActivationFunction, random));
}ну и соответствующие методы:
CreateNeurons()
/// <summary>
/// Возвращает список нейронов, инициализированных весовыми коэффициентами
/// </summary>
/// <param name="neuronsCount">количество нейронов</param>
/// <param name="weightsCount">количество весовых коэффициентов в каждом нейроне</param>
/// <param name="weightsMinValue">левая граница интервала случайных чисел</param>
/// <param name="weightsMaxValue">правая граница интервала случайных чисел</param>
/// <param name="activationFunction">функция активации</param>
/// <param name="random">экземпляр генератора случайных чисел</param>
/// <returns></returns>
private List<Neuron> CreateNeurons(int neuronsCount, int weightsCount, double weightsMinValue, double weightsMaxValue, Func<double, double> activationFunction, Random random)
{
List<Neuron> neurons = new List<Neuron>();
for (int i = 0; i < neuronsCount; i++)
{
List<double> weights = CreateRandomWeights(weightsCount, weightsMinValue, weightsMaxValue, random);
neurons.Add(new Neuron(activationFunction, weights, CreateRandomValue(random, weightsMinValue, weightsMaxValue, i)));
}
return neurons;
}CreateRandomWeights()
/// <summary>
/// Возвращает список весовых коэффициентов инициализированных случайными значениями
/// </summary>
/// <param name="weightsCount">количество весовых коэффициентов</param>
/// <param name="minValue">левая граница интервала случайных чисел</param>
/// <param name="maxValue">правая граница интервала случайных чисел</param>
/// <param name="random">экземпляр генератора случайных чисел</param>
/// <returns></returns>
private List<double> CreateRandomWeights(int weightsCount, double minValue, double maxValue, Random random)
{
List<double> weights = new List<double>();
for (int i = 0; i < weightsCount; i++)
weights.Add(CreateRandomValue(random, minValue, maxValue, i));
return weights;
}CreateRandomValue()
/// <summary>
/// Возвращает случайное число в заданном интервале
/// </summary>
/// <param name="random">экземпляр генератора случайных чисел</param>
/// <param name="minValue">левая граница интеравала</param>
/// <param name="maxValue">правая граница интеравала</param>
/// <param name="currentIndex">текущий индекс генерируемого значения</param>
/// <returns></returns>
private double CreateRandomValue(Random random, double minValue, double maxValue, int currentIndex)
{
double randomDouble = random.NextDouble() * (maxValue - minValue) + minValue;
if (currentIndex % 2 == 0) // Будем чередовать знаки через один
return -randomDouble;
return randomDouble;
} Метод CreateRandomValue() принимает аргумент currentIndex, от которого, как было сказано выше, будет зависеть знак рандомного значения.
Второй конструктор просто принимает заранее подготовленные слои:
Network(). Конструктор для инициализации сети подготовленными слоями
public Network(List<Layer> HiddenLayers, Layer OutputLayer)
{
this.HiddenLayers = HiddenLayers;
this.OutputLayer = OutputLayer;
}После обучения нейросети неплохо бы сохранить скорректированные весовые коэффициенты в файлы:
Запись весовых коэффициентов в файл
/// <summary>
/// Записывает данные по скрытым слоям (количество скрытых слоев, их размерности, пороговые значения, весовые коэффициенты) в файл
/// </summary>
/// <param name="fileName">имя файла для записи</param>
public void WriteHiddenWeightsToCSVFile(string fileName)
{
if (HiddenLayers == null)
return;
TextWriter textWriter = new StreamWriter(fileName);
textWriter.WriteLine(string.Format("{0};{1}", "hiddenLayersDimensions", string.Join(";", HiddenLayers.Select(x => x.Neurons.Count))));
foreach (Layer hiddenLayer in HiddenLayers)
foreach (Neuron neuron in hiddenLayer.Neurons)
textWriter.WriteLine("{0};{1}", neuron.Bias, string.Join(";", neuron.Weights));
textWriter.Close();
}
/// <summary>
/// Записывает пороговые значения и весовые коэффициенты выходного слоя сети в файл
/// </summary>
/// <param name="fileName">имя файла для записи</param>
public void WriteOutputWeightsToCSVFile(string fileName)
{
TextWriter textWriter = new StreamWriter(fileName);
foreach (Neuron neuron in OutputLayer.Neurons)
textWriter.WriteLine("{0};{1}", neuron.Bias, string.Join(";", neuron.Weights));
textWriter.Close();
} Методы для чтения весовых коэффициентов вынесены в отдельный класс.
Прямой проход
Следующий метод класса Network запускает алгоритм прямого распространения сигнала по сети и возвращает выходной сигнал:
/// <summary>
/// Запускает алгоритм прямого распространения сигнала и возвращает ответ от сети
/// </summary>
/// <param name="functionSignal">функциональный сигнал (стимул), поступающий на вход нейросети</param>
/// <returns></returns>
public List<double> MakePropagateForward(List<double> functionSignal)
{
// Если имеются скрытые слои, то передаем сигнал по скрытым слоям
if (HiddenLayers != null)
foreach (Layer hiddenLayer in HiddenLayers)
functionSignal = SetInputSignalAndInducedLocalFieldAndReturnOutputSignal(hiddenLayer, functionSignal);
// Возвращаем сигнал от выходного слоя
return SetInputSignalAndInducedLocalFieldAndReturnOutputSignal(OutputLayer, functionSignal);
}В этом методе входной сигнал, который представляет из себя вектор-изображение из 784 элементов, передается сначала по скрытым слоям (если они есть), а затем от выходного слоя возвращается сигнал из 10 значений. Каждое из этих 10 значений представляет собой вероятность предсказания той или иной цифры.
В процессе передачи сигнала от слоя к слою метод с длинным названием также устанавливает свойства InputSignals класса Layer и InducedLocalField класса Neuron:
/// <summary>
/// Задает слою входной сигнал, устанавливает локальные индуцированные поля нейронов и возвращает выходной сигнал
/// </summary>
/// <param name="layer">слой</param>
/// <param name="functionSignal">входной сигнал</param>
/// <returns>выходной сигнал</returns>
private List<double> SetInputSignalAndInducedLocalFieldAndReturnOutputSignal(Layer layer, List<double> functionSignal)
{
layer.InputSignals = functionSignal;
foreach (Neuron neuron in layer.Neurons)
neuron.SetInducedLocalField(functionSignal);
return layer.ProduceSignals();
}Алгоритм обратного распространения
Как было сказано в самом начале статьи, реализовывать я буду последовательный (стохастический) режим обучения:
Описание последовательного режима обучения (гл. 4, раздел 4.3)

Процесс обучения начинается с метода Train() класса Network:
Train()
/// <summary>
/// Запускает алгоритм обучения нейронной сети
/// </summary>
/// <param name="imagesFileName">путь к бинарному файлу MNIST с изображениями</param>
/// <param name="labelsFileName">путь к бинарному файлу MNIST с метками (наименованиями цифр)</param>
/// <param name="learningRateParameter">параметр скорости обучения</param>
/// <param name="numberOfEpochs">количество эпох</param>
public void Train(string imagesFileName, string labelsFileName, double learningRateParameter, int numberOfEpochs)
{
for (int e = 0; e < numberOfEpochs; e++)
{
// Получаем изображения
IEnumerable<TestCase> testCases = FileReaderMNIST.LoadImagesAndLables(labelsFileName, imagesFileName);
foreach (TestCase test in testCases)
{
// Конвертируем изображение в функциональный сигнал
List<double> functionSignal = ImageHelper.ConvertImageToFunctionSignal(test.Image);
// Получаем ожидаемый ответ
List<double> desiredResponse = GetDesiredResponse(test.Label);
// Получаем ответ от сети (прямой проход)
List<double> outputSignal = MakePropagateForward(functionSignal);
// Вычисляем сигнал ошибки как разность между ожидаемым и фактическим ответом нейросети
List<double> errorSignal = GetErrorSignal(desiredResponse, outputSignal);
// Запускаем алгоритм обратного распространения ошибки
MakePropagateBackward(errorSignal, learningRateParameter);
}
Console.WriteLine("epoch " + e.ToString() + " finished"); // Выводим в консоль прогресс выполнения
}
}который содержит в себе метод для запуска алгоритма обратного распространения:
/// <summary>
/// Запускает алгоритм обратного распространения ошибки
/// </summary>
/// <param name="errorSignal">сигнал ошибки</param>
/// <param name="learningRateParameter">параметр скорости обучения</param>
private void MakePropagateBackward(List<double> errorSignal, double learningRateParameter)
{
// Вычисляем локальные градиенты для выходного слоя
OutputLayer.CalculateAndSetLocalGradients(errorSignal);
// Корректируем весовые коэффициенты и пороговые значения выходного слоя
OutputLayer.AdjustWeightsAndBias(learningRateParameter);
// Если скрытых слоев нет, то заканчиваем процесс
if (HiddenLayers == null)
return;
// Устанавливаем выходной слой как предыдущий
// (для обратного прохода это тот слой, который расположен правее)
Layer previousLayer = OutputLayer;
// Идем от последнего скрытого слоя к первому
for (int i = HiddenLayers.Count - 1; i >= 0; i--)
{
// Вычисляем локальные градиенты
HiddenLayers[i].CalculateAndSetLocalGradients(previousLayer);
// Корректируем весовые коэффициенты и пороговые значения
HiddenLayers[i].AdjustWeightsAndBias(learningRateParameter);
previousLayer = HiddenLayers[i];
}
}По комментариям я думаю понятно, что тут происходит. Опишу входящие сюда методы подробней.
Зная сигнал ошибки, мы можем вычислить локальные градиенты для нейронов выходного слоя:
/// <summary>
/// Вычисляет и устанавливает нейронам ВЫХОДНОГО слоя локальные градиенты
/// </summary>
/// <param name="errorSignal">сигнал ошибки</param>
internal void CalculateAndSetLocalGradients(List<double> errorSignal)
{
for (int i = 0; i < Neurons.Count; i++)
Neurons[i].SetLocalGradient(errorSignal[i] * ActivationFunctions.SigmoidFunctionsDerivative(Neurons[i].InducedLocalField));
}по формуле:
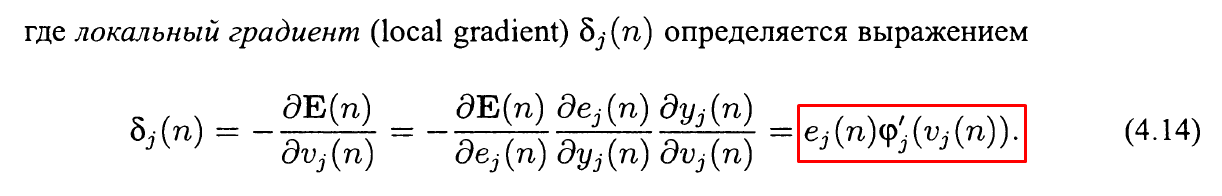
Вычислив локальные градиенты выходного слоя — корректируем весовые коэффициенты и пороговые значения нейронов выходного слоя:
/// <summary>
/// Корректирует весовые коэффициенты и пороговое значение
/// </summary>
/// <param name="learningRateParameter">параметр скорости обучения</param>
/// <param name="inputSignals">входной сигнал нейрона, заданный при прямом проходе</param>
internal void AdjustWeightsAndBias(double learningRateParameter, List<double> inputSignals)
{
for (int i = 0; i < Weights.Count; i++)
{
Weights[i] += learningRateParameter * LocalGradient * inputSignals[i]; // Корректируем весовые коэффициенты
Bias += learningRateParameter * LocalGradient; // Корректируем пороговое значение (inputSignal для него равен 1)
}
}по формуле:
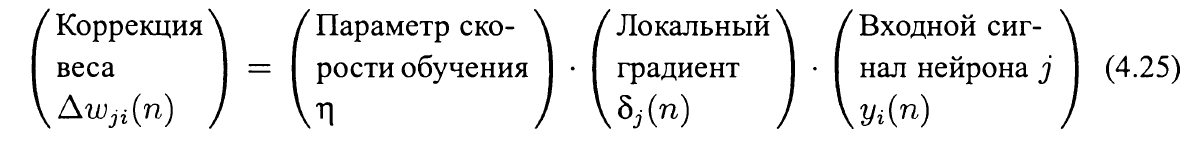
Затем вычисляем локальные градиенты скрытых слоев:
/// <summary>
/// Вычисляет и устанавливает нейронам СКРЫТОГО слоя локальные градиенты на основе предыдущего слоя в алгоритме обратного распространения
/// </summary>
/// <param name="previousLayer">предыдущий слой (расположенный правее текущего)</param>
internal void CalculateAndSetLocalGradients(Layer previousLayer)
{
for (int i = 0; i < Neurons.Count; i++)
{
// Получаем весовые коэффициенты, непосредственно связанный с этим нейроном
List<double> associatedWeights = GetAssociatedWeights(previousLayer, i);
// Подсчитываем внутреннюю сумму
double innerSum = GetInnerSum(associatedWeights, previousLayer);
// Вычисляем и устанавливаем нейрону скрытого слоя локальный градиент
Neurons[i].SetLocalGradient(innerSum * ActivationFunctions.SigmoidFunctionsDerivative(Neurons[i].InducedLocalField));
}
}по формуле:
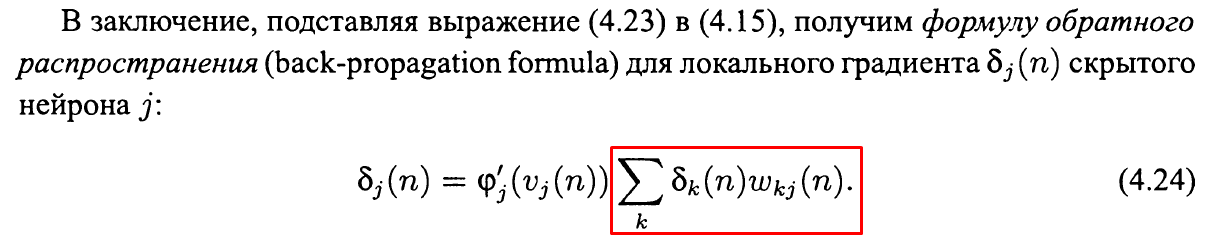
После того, как локальные градиенты нейронов скрытого слоя вычислены, по формуле (4.25) корректируем весовые коэффициенты и пороговые значения.
Данные вычисления проводятся для всех слоев в обратном направлении. После того, как все весовые коэффициенты и пороговые значения откорректированы, подаем на вход новый обучающий пример, находим сигнал ошибки и запускаем новую итерацию алгоритма обратного распространения ошибки.
Заключение
В результате экспериментов было установлено, что нейросеть неплохо обучается, если на обратном проходе не корректировать пороговые значения, т.е. закомментировать вот эту строчку:
internal void AdjustWeightsAndBias(double learningRateParameter, List<double> inputSignals)
{
for (int i = 0; i < Weights.Count; i++)
{
Weights[i] += learningRateParameter * LocalGradient * inputSignals[i]; // Корректируем весовые коэффициенты
// Bias += learningRateParameter * LocalGradient; // Корректируем пороговое значение (inputSignal для него равен 1)
}
}В общем, как бы там ни было, обучение нейросети — процесс очень творческий и неоднозначный и требует довольно долгих расчетов и экспериментов. И, как утверждает автор оригинальной статьи, вместо тюнинга параметров нейросети и достижения более точных результатов лучше перейти к реализации принципиально нового типа сетей — сверточных нейронных сетей. Но об этом, наверное, в другой раз.
В статье я почти ни слова не сказал о производительности, хотя это и не является главной темой работы. Скажу лишь, что на моем Intel(R) Core(TM) i5-8250U CPU @ 1.60GHz 1.80GHz c 16 ГБ ОЗУ процесс обучения с одним скрытым слоем (80 нейронов) в 16 эпох занял примерно 40 мин (да, не быстро!). Поэтому оставляю за читателем право максимально распараллелить все возможные процессы (Parallel.For, PLINQ и т.п. вам в помощь).
Надеюсь Вам была полезна моя статья!
С наступающим Рождеством!
Мира, добра и чистого кода!
Комментарии (13)

lgorSL
07.01.2023 00:09+5Статья хороша для понимания "как устроены нейронки", но реальные сетки пишутся сильно по-другому.
Весь слой целиком задаётся как матрица (возможно, даже 3-4-мерная) и вычисления выражаются через них. Складывать и перемножать матрицы быстро человечество уже давно умеет.Если интересно машинное обучение - вот примеры с распознаванием mnist в pytorch и keras.
В Pytorch есть вычисление градиентов, в tensorflow 2.0 - тоже добавили.

kraglik
07.01.2023 00:11+5Небольшой совет: нынче применяют автодифференцирование :-)
Есть такая классная вещь, как Chain Rule, оно лежит в основе того же PyTorch.
Я как раз на днях имплементил, можно в однофайловом примере посмотреть, как это устроено. Легко повторяется при наличии NumPy/CuPy и терпения. Заранее извиняюсь за черновой код :)
Если вкраце: есть заранее записанные алгоритмы для вычисления производных простых составляющих, из них потом как из лего строят более сложные функции. Производная этой сложной функции элементарно вычисляется, если известно, как считать производные ее составляющих.И да, @lair прав - в классических нейронных сетях все-таки операции над матрицами происходят, а не ООП. Поиграйтесь с тензорами, в шарпах они вроде как имеются.
Начинание хорошее, продолжайте!
Green21 Автор
07.01.2023 00:14+1Нечайно минусовал)
Хорошо, спасибо за совет!
И правда, я немного поэксперементировал с Parallel и PLINQ, но никакого прироста производительности не ощутил.

apelsyn
07.01.2023 06:51+1
Много лет назад вот в статье "Нейронные сети на Javascript", я делал реализацию на JS, только сам backpropagation я использовал из готовой билиотеки "BranJS" а больше фокус на визуализацию.
Несколько идей по самой реализации:
- В качестве дополнительной нормализации (для песочницы) необходимо определять область с изображением и центрировать ее, иначе если написать цифру не по центру или слишком маленькую в углу то результат будет значительно хуже.
- Переводить из GrayScale в Black and White означает некую потерю информации о изображении. Это ускоряет обучение но все же ведет к потери качества.
- Из соображений производительности сейчас больше применяется пакетный (batch) вариант градиентного спуска

Mingun
07.01.2023 09:27+2Гм… что-то тут не так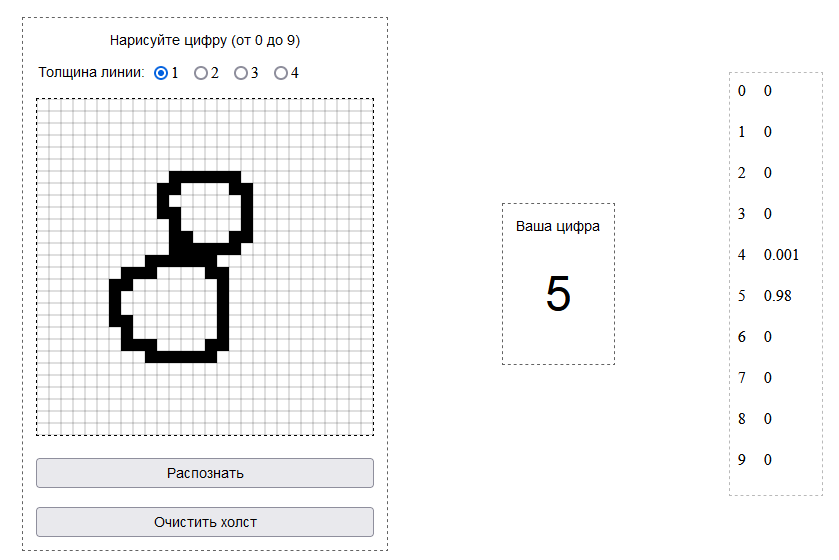
Причём, это я ещё по углам натыкал пикселей, чтобы линия более явно чувствовалась, но уверенность нейросети в цифре «5» только росла.

lgorSL
07.01.2023 16:03-1Сетка после "расслоения" изображения в 784 сигнала ничего не знает про геометрию и даже смещение модели вбок на один пиксель может сильно испортить предсказание. Собственно, и количество верных предсказаний такой сетки - 95%.
Если использовать свёрточные слои + max pooling для уменьшения картинки и извлечения признаков, (несколько раз) а только потом "расслоить" маленькую картинку с высокоуровневыми признаками и ещё несколько слоёв как в статье добавить - тогда можно будет достичь 99% точных предсказаний.

Mingun
07.01.2023 16:18-1Значит, обучающая выборка не была достаточно хорошей, раз нейросеть так легко ломается.

Green21 Автор
07.01.2023 16:25Если посмотрите по коммитам, сначала я вообще хотел нагенерить сам обучающую выборку в пейнте)) Но после 2К изображений мне надоело это занятие и я начал искать...и вышел на mnist))

lgorSL
07.01.2023 16:50+1Нет. Это значит, что выбранная архитектура нейросети не позволяет достичь высокой точности. На датасете mnist тренируют и сравнивают нейронки уже много лет.
Тут результаты: https://en.wikipedia.org/wiki/MNIST_database Практически все лучше результаты принадлежат свёрточным нейронным сетям, причём некоторые без какого-либо препроцессинга и дополнения обучающей выборки выдают error rate 0.25% и меньше
Mingun
07.01.2023 19:41Я не говорю, что датасет MNIST плох. Я говорю, что обучающую выборку из него сформировали недостаточно полную. Условно, если сдвинуть всю картинку на пиксель влево и она начнёт успешно правильно распознаваться, то это значит, что выбранная архитектура сети таки позволяет добиться высокой точности, просто нейросеть не научили как следует.

Green21 Автор
07.01.2023 16:22Да, эксперименты в песочнице меня самого не очень порадовали. Я думал, раз нейронка удачно распознала >95% изображений, то в песочнице она будет почти всегда предсказывать правильно. Но не тут то было. Я заметил, что некоторые цифры она предсказывает лучше остальных.



lair
Бесполезно это. Не зря в каждом курсе про машинное обучение (и нейронные сети) расказывают про вычисления над векторами и матрицами. Пока вы для вычислений пытаетесь следовать ОО-парадигме, вы так и будете тратить очень много на накладные расходы.