Задача теплопроводности методом продольно-поперечной прогонки средствами MPI / forpes.ru

Главная
Задача теплопроводности методом продольно-поперечной прогонки средствами MPI

Задача теплопроводности методом продольно-поперечной прогонки средствами MPI +10

24.12.2022 11:45

AshBlade 26 1600 Источник

Приветствую.

Недавно в бэклоге появилась задача моделирования процесса теплопроводности. На осознание формулы и нахождения решения ушло немало времени и, чтобы у вас не возникали такие же трудности, хочу поделиться решением.

Постановка задачи

Задача теплопроводности - это задача математического моделирования.

На вход дается температура в исходном пространстве (сетке), а на выходе - температура через некоторое время.

Математическое представление следующее:

${\frac {\partial u}{\partial t}}-{\lambda}^{2}\left({\frac {\partial ^{2}u}{\partial x_{1}^{2}}}+{\frac {\partial ^{2}u}{\partial x_{2}^{2}}}+\cdots +{\frac {\partial ^{2}u}{\partial x_{n}^{2}}}\right)=f(x,t)$

где

- координаты в декартовом пространстве
${\partial t}$ - дельта времени
${\partial u}$ - изменения температуры в каждой точке
${\lambda}$ - коэффициент теплопроводности
- функция тепловых источников. В нашей задаче внутри сетки нет источников тепла, поэтому она равна 0 и акцентировать внимание на ней не будем.

Для текущей задачи с двумерной сеткой и отсутствием точек внутренних источников тепла функция будет выглядеть следующим образом

${\frac {\partial u}{\partial t}}-{\lambda}^{2}\left({\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}\right)=0$

Интерпретировать ее можно таким образом:

Изменение температуры на слое через какое-то количество времени равно сумме изменений температуры по каждому направлению с учетом коэффициента теплопроводности.

По факту мы имеем задачу Коши. Решение для нее существует, если даны граничные условия.

Граничные и начальные условия нам тоже даны

$x {\in}[0;1]\\y{\in}[0;0,5]$ $u(x, y, 0) = 300\\u(0, y, t)=600, u(1, y, t) = 1200\\u(x, 0, t)=600(1 + x), u(x, 0.5, t)=600(1 + x^3)$

Расшифровка условий

изменяется от 0 до 1

изменяется от 0 до 0.5

300 - начальная температура пространства

Температура при x = 0: 600, при x = 1: 1200

Температура при y = 0: 600(1 + x), при y = 0.5: 600(1 + x^3)

Но в формуле также присутствует и коэффициент теплопроводности. Для задачи он задается условием

${\lambda} = \begin{cases} 10^{-2}, x{\in}[0.25; 0.65], y{\in}[0.1;0.25] \\ 10^{-4} \end{cases}$

Продольно-поперечная прогонка

Существует множество готовых численных методов. Для решения будем использовать метод конечных разностей с неявной схемой.

Суть этого метода в последовательном нахождении температуры на следующем временном слое проходясь по всем направлениям поочередно. При прохождении по очередному слою мы находим состояние сетки в +1/n слое, где n - количество направлений.

Например, пусть нам дана 2-мерная сетка (X и Y), и ее состояние на 3 слое. Тогда:

Проходимся по X, находим состояние сетки в момент 3+½
Проходимся по Y, находим состояние в момент 4.

На этом итерация заканчивается

По аналогии с 3-мерной сеткой:

Проходимся по X, находим состояние 3+⅓
Проходимся по Y, находим состояние 3+⅔
Проходимся по Z, находим состояние 4

Метод прогонки

Метод прогонки - алгоритм решения систем линейных уравнений вида

где - трехдиагональная матрица вида

$M={\begin{pmatrix}C_{0}&B_{0}&0&0&\dots &0&0&0\\A_{1}&C_{1}&B_{1}&0&\dots &0&0&0\\0&A_{2}&C_{2}&B_{2}&\dots &0&0&0\\\dots &\dots &\dots &\dots &\dots &\dots &\dots &\dots \\\dots &\dots &\dots &\dots &\dots &\dots &\dots &\dots \\\dots &\dots &\dots &\dots &\dots &A_{n-1}&C_{n-1}&B_{n-1}\\0&0&0&0&\dots &0 &A_{n}&C_{n}\end{pmatrix}}$

Сама прогонка состоит из 2 этапов:

Прямая прогонка - нахождение коэффициентов ${\alpha}$ и ${\beta}$
Обратная прогонка - нахождение искомых значений

Метод состоит в следующем. Даны A, B, C - коэффициенты матрицы на каждой из строк и граничные условия - максимальное и минимальное значения на границах.

Прямая прогонка - находим коэффициенты ${\alpha}$ и ${\beta}$ . Коэффициенты находятся с помощью системы уравнений

${\displaystyle {\begin{cases}\alpha _{i}={\dfrac {-B_{i}}{A_{i}\alpha _{i-1}+C_{i}}}\\\beta _{i}={\dfrac {F_{i}-A_{i}\beta _{i-1}}{A_{i}\alpha _{i-1}+C_{i}}}\end{cases}}}\space ,\space\space i=1\dots N-1$

При этом ${\alpha}_0 = {\alpha_N} = 0$ , а значения ${\beta}_0$ и ${\beta}_N$ определяются из соответствующих краевых условий.

Для задачи теплопроводности ${\beta}_0 = min, {\beta}_N = max$ , где - температура в начале сетки, а - в конце для соответствующего направления. Например, если мы проходимся по направлению , то ,

Алгоритм работы такой:

Инициализируем начальные значения: ${\alpha}_0$ и ${\beta}_0$
Находим ${\alpha}_i$ и ${\beta}_i$ на основании ${\alpha}_{i-1}$ и ${\beta}_{i - 1}$

Обратная прогонка - находим исходные . Они находятся также при помощи формулы

$y_i={\alpha}_i y_{i + 1} + {\beta}_i \space,\space\space i=N-2\dots1\\y_N=max$

Алгоритм следующий:

Инициализируем начальное значение -
Находим на основании $y_{i + 1}$

Как можно заметить прямая прогонка - прогоночный коэффициент изменяется от 1 до , при обратной прогонке наоборот - от до 0.

Не забываем о матрице . Для удобства, представим матрицу в виде 3 других: . Где каждая матрица представляет свои коэффициенты.

В задаче теплопроводности их значения находятся через коэффициенты теплопроводности:

$A_{i,j} = - {\frac {\lambda_{i, j-1/2}} { 2h^2 }} \\ B_{i,j} = - {\frac {\lambda_{i, j+1/2}} { 2h^2 }} \\ C_{i, j} = {\frac 1 {\tau}} - A_{i,j} - B_{i, j}$

где

${\lambda}_{i,j{\pm}1/2} = {\frac {{\lambda}_{i,j{\pm}1} - {\lambda}_{i,j}} 2 }$ ${\lambda}_{i{\pm}1/2, j} = {\frac {{\lambda}_{i{\pm}1, j} - {\lambda}_{i,j}} 2 }$ - коэффициенты теплопроводности. Причем, первая используется при прогонке по направлению , а последнее - по
$\tau$ - шаг по времени. Задается нами. Например, 0.2
- шаг в пространстве. Например, если мы разбили направление x на 10 частей, то

$h={\frac {1 - 0} {10} }=0.1$

Теперь мы имеем все, чтобы сделать функцию решения задачи прогонки

void solveThomas(const double* F,
                    const double* lambda,
                    const int length,
                    const double min,
                    const double max,
                    const double step,
                    const double timeStep,
                    double* y) {
    const auto coefficient = 1.0 / (2 * step * step);

    double A[length], B[length], C[length];
    for (int i = 0; i < length; ++i) {
        A[i] = - avg(lambda[i + 1], lambda[i]) / 2 * coefficient;
        B[i] = - avg(lambda[i + 1], lambda[i + 2]) / 2 * coefficient;
        C[i] = 1 / timeStep - A[i] - B[i];
    }

    double alpha[length], beta[length];
    alpha[0] = alpha[length - 1] = 0;
    beta[0] = min;
    beta[length - 1] = max;

    for (int i = 0; i < length - 2; ++i) {
        alpha[i + 1] = - B[i + 1] / (C[i + 1] + A[i + 1] * alpha[i]);
        beta[i + 1] = (F[i + 1] - A[i + 1] * beta[i]) / (C[i + 1] + A[i + 1] * alpha[i]);
    }

    y[length - 1] = max;
    for (int i = length - 2; i >= 0; i--) {
        y[i] = alpha[i] * y[i + 1] + beta[i];
    }
}

Так как мы решаем задачу в одномерном случае, то матрицы представляем в виде массива, размером в длину сетки по текущему направлению.

Но у нас есть еще и , которое необходимо для нахождения на следующем слое. Для получения на следующем слое нам пригодятся следующие формулы

$\begin{cases} A_{i, j}y_{i-1, j}^{n + 1/2} + C_{i,j}y_{i, j}^{n + 1/2} + B_{i,j}y_{i + 1, j}^{n + 1/2} = F_{i, j}^{n},\space\space j=1 \dots, N_y - 1 \\ F_{i, j}^{n + 1/2} = {\frac {y_{i, j}^{n + 1/2}} {\tau} + {\frac {{\lambda}_{i+1/2, j}(y_{i+1, j}^{n+1/2} - y_{i, j}^{n+1/2}) - {\lambda}_{i-1/2, j}(y_{i, j}^{n+1/2} - y_{i-1, j}^{n+1/2})} {2h_x^2} }} \end{cases} \\ \begin{cases} A_{i, j}y_{i, j-1}^{n + 1} + C_{i,j}y_{i, j}^{n + 1} + B_{i,j}y_{i, j+1}^{n + 1} = F_{i, j}^{n + 1/2},\space\space i=1 \dots, N _x- 1 \\ F_{i, j}^{n} = {\frac {y_{i, j}^{n}} {\tau} + {\frac {{\lambda}_{i, j+1/2}(y_{i, j+1}^n - y_{i, j}^n) - {\lambda}_{i, j-1/2}(y_{i, j}^n - y_{i, j-1}^n)} {2h_y^2} }} \end{cases}$

где

- количество разбиений по направлению X
- количество разбиений по направлению Y
Верхние коэффициенты - временной слой

Объяснение формул

Первая скобка рассказывает как делать итерацию по :

Делаем прогонку по направлению и находим $y^{n+1/2}$
Вычисляем $F^{n+1/2}$ - значения на n+1/2 слое

Вторая скобка рассказываем как делать итерацию по Y:

Делаем прогонку по направлению и находим $y^{n+1}$
Вычисляем $F^{n+1}$ - значения на n+1 слое (n можно заменить на n+1)

Заметим, что при вычислении на каком-либо направлении мы зависим, только от тех , которые нашли для направления при соответствующих коэффициентах прогонки. Грубо говоря, чтобы получить значения на соответствующем слое $(F^{n + 1/2}, F^{n + 1})$ нам требуются только те , которые мы нашли из проведенной прогонки на слое. Если мы делали прогонку по с и нашли значения $y_{1, j}^{n + 1/2}$ , то для нахождения $F_{1, j}^{n+1/2}$ необходимы только $y_{1, j}^{n + 1/2}$

Теперь мы можем написать функцию для восстановления значений по данным

void restoreF(const double* y,
              const double* lambda,
              const int size,
              const double step,
              const double timeStep,
              double* F) {
    const double coefficient = 1 / (2 * step * step);
    for (int i = 1; i < size - 1; ++i) {
        double lambdaPlusHalf = avg(lambda[i], lambda[i + 1]);
        double lambdaMinusHalf = avg(lambda[i], lambda[i - 1]);
        double temp = lambdaPlusHalf * (y[i + 1] - y[i]) - lambdaMinusHalf * (y[i] - y[i - 1]);
        F[i] = y[i] / timeStep + temp * coefficient;
    }
}

Последовательное решение

Теперь мы можем решить задачу в 2-мерном случае. Все что нам осталось сделать - инициализировать начальные данные и правильно оформить логику прогонки: обернуть итерации в циклы в правильной последовательности.

double getLambda(double x, double y) {
    return 0.25 <= x && x <= 0.65 &&
    0.1 <= y && y <= 0.25 ? 0.01 : 0.0001;
}

double avg(double left, double right) {
    return (left + right) / 2;
}

void solveThomas(const double* F,
                    const double* lambda,
                    const int length,
                    const double min,
                    const double max,
                    const double step,
                    const double timeStep,
                    double* y) {
    const auto coefficient = 1.0 / (2 * step * step);

    double A[length], B[length], C[length];
    for (int i = 0; i < length; ++i) {
        A[i] = - avg(lambda[i + 1], lambda[i]) / 2 * coefficient;
        B[i] = - avg(lambda[i + 1], lambda[i + 2]) / 2 * coefficient;
        C[i] = 1 / timeStep - A[i] - B[i];
    }

    double alpha[length], beta[length];
    alpha[0] = alpha[length - 1] = 0;
    beta[0] = min;
    beta[length - 1] = max;

    for (int i = 0; i < length - 2; ++i) {
        alpha[i + 1] = - B[i + 1] / (C[i + 1] + A[i + 1] * alpha[i]);
        beta[i + 1] = (F[i + 1] - A[i + 1] * beta[i]) / (C[i + 1] + A[i + 1] * alpha[i]);
    }

    y[length - 1] = max;
    for (int i = length - 2; i >= 0; i--) {
        y[i] = alpha[i] * y[i + 1] + beta[i];
    }
}

void restoreF(const double* y,
              const double* lambda,
              const int size,
              const double step,
              const double timeStep,
              double* F) {
    const double coefficient = 1 / (2 * step * step);
    for (int i = 1; i < size - 1; ++i) {
        double lambdaPlusHalf = avg(lambda[i], lambda[i + 1]);
        double lambdaMinusHalf = avg(lambda[i], lambda[i - 1]);
        double temp = lambdaPlusHalf * (y[i + 1] - y[i]) - lambdaMinusHalf * (y[i] - y[i - 1]);
        F[i] = y[i] / timeStep + temp * coefficient;
    }
}

int main(int argc, char** argv) {
    const int size = 10;
    const double timeStep = 0.1;
    const double tLeft = 600;
    const double tRight = 1200;
    const double xMin = 0;
    const double xMax = 1;
    const double yMin = 0;
    const double yMax = 0.5;
    const double xStep = (xMax - xMin) / size;
    const double yStep = (yMax - yMin) / size;

    // y - исходная температура
    double temperatureByX[size][size];
    double lambdaByX[size][size];
    // F
    double FByX[size][size];
    for (int i = 0; i < size; ++i) {
        auto x = i * xStep;
        for (int j = 0; j < size; ++j) {
            auto y = j * yStep;
            lambdaByX[i][j] = getLambda(x, y);
            temperatureByX[i][j] = 300;
            FByX[i][j] = 0;
        }
    }

    for (int i = 0; i < size; ++i) {
        restoreF(temperatureByX[i], lambdaByX[i], size, xStep, timeStep, FByX[i]);
    }

    // Меняю строки и столбцы
    double temperatureByY[size][size];
    double FByY[size][size];
    double lambdaByY[size][size];

    for (int y = 0; y < size; ++y) {
        for (int x = 0; x < size; ++x) {
            temperatureByY[y][x] = temperatureByX[x][y];
            FByY[y][x] = FByX[x][y];
            lambdaByY[y][x] = lambdaByX[x][y];
        }
    }


    const int iterations = 100;
    for (int t = 0; t < iterations; ++t) {
        // Вычисляю yn+1/2
        for (int x = 0; x < size; ++x) {
            solveThomas(FByX[x], lambdaByX[x], size, tLeft, tRight, xStep, timeStep, temperatureByX[x]);
        }

        // Вычисляю Fn+1/2
        for (int x = 0; x < size; ++x) {
            restoreF(temperatureByX[x], lambdaByX[x], size, xStep, timeStep, FByX[x]);
        }

        // Обновляю значения температуры и F по Y
        for (int y = 0; y < size; ++y) {
            for (int x = 0; x < size; ++x) {
                FByY[y][x] = FByX[x][y];
            }
        }

        // Вычисляю yn+1
        for (int y = 0; y < size; ++y) {
            double x = xMin + y * xStep;
            solveThomas(FByY[y], lambdaByY[y], size, 600 * (1 + x), 600 * (1 + x * x * x), yStep, timeStep, temperatureByY[y]);
        }

        // Вычисляю Fn+1
        for (int y = 0; y < size; ++y) {
            restoreF(temperatureByY[y], lambdaByY[y], size, yStep, timeStep, FByY[y]);
        }


        // Обновляю значения температуры и F по X
        for (int x = 0; x < size; ++x) {
            for (int y = 0; y < size; ++y) {
                temperatureByX[x][y] = temperatureByY[y][x];
                FByX[x][y] = FByY[y][x];
            }
        }
    }

}

Параллельная реализация

Можно заметить, что при прогонке по каждому направлению, значения независят друг от друга. Например, при прогонке по X, строки 1 и 2 не зависят друг от друга. Это хорошая точка для распараллеливания.

Данная задача - CPU-bound. Для них подходит распараллеливание по процессам. Будем использовать MPI - интерфейс для обмена сообщениями между процессами. Познакомиться с ним можно здесь.

Функции для распараллеливания

Все что нам нужно - передать массивы и по нужным направлениям. Для передачи массивов данных по всем направлениям существует функция MPI_Scatter

int MPI_Scatter(const void *sendbuf, int sendcount, MPI_Datatype sendtype, 
                void *recvbuf, int recvcount, MPI_Datatype recvtype, 
                int root, MPI_Comm comm)

Она передает массивы фиксированной длины на все процессы, включая отправитель. Но мало передать, нужно и получить обратно. Для этого тоже есть функция - MPI_Gather

int MPI_Gather(const void *sendbuf, int sendcount, MPI_Datatype sendtype, 
               void *recvbuf, int recvcount, MPI_Datatype recvtype, 
               int root, MPI_Comm comm)

Она собирает массивы фиксированного размера со всех процессов, включая корень.

В итоге, итерация будет выглядеть следующим образом:

Передаем данные по направлению X по процессам
Находим температуру
Находим F
Возвращаем посчитанные данные на главный процесс
Обновляем значения температуры и F
Передаем данные по направлению X по процессам
Находим температуру
Находим F
Возвращаем посчитанные данные на главный процесс
Обновляем данные температуры и F

Вспомогательные детали

Для удобства, размеры сетки в обе стороны одинаковые. Поэтому количество процессов сделаем равным размеру сетки в одном направлении. Проверка при старте приложения.

int processesCount;
MPI_Init(&argc, &argv);
MPI_Comm_size(MPI_COMM_WORLD, &processesCount);
if (processesCount != size) {
    if (rank == 0) {
        std::cout << "Количество процессов должно быть " << size << std::endl;
    }
    MPI_Finalize();
    return 0;
}

Для более удобного логического представления программы сделаем ветвление по номеру процесса: мастер попадет в свою секцию, слейвы попадут в свою.

int rank;
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
if (rank == 0) {
  // Работа главного процесса
} else {
  // Работа слейвов
}

Свой тип данных для колоночной передачи матрицы

В нашей предыдущей реализации мы использовали 2 типа массивов для хранения: по X и по Y, а при слиянии результатов меняли их местами. Это не совсем эффективно, т.к. размер матрицы растет экспоненциально. Было бы неплохо передавать матрицу по столбцам и по строкам без необходимости каких-либо манипуляций. Решение - свой тип данных.

В MPI свой тип данных можно создать с помощью функции MPI_Type_vector

int MPI_Type_vector(int count, int blocklength, int stride, 
                    MPI_Datatype oldtype,
                    MPI_Datatype *newtype)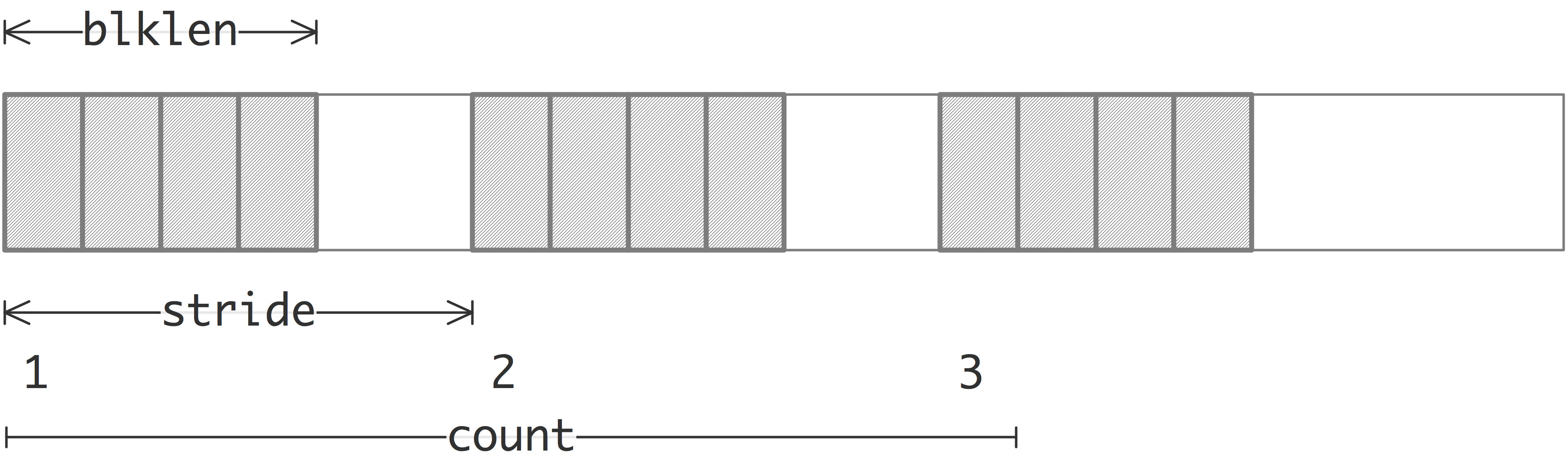

Логическое представление влияния передаваемых аргументов функции MPI_Type_vector

Для передачи матрицы по столбцам создим новый тип данных таким способом:

// size - размер матрицы в одном направлении
MPI_Datatype matrixColumnsType;
// Всего у нас size столбцов, 
// в каждом из которых нужно взять 1 число 
// из блока в size чисел
// типа double (MPI_DOUBLE)
MPI_Type_vector(size, 1, size, MPI_DOUBLE, &matrixColumnsType);
MPI_Type_commit(&matrixColumnsType);

Но есть проблема. Если использовать созданый тип данных при передаче, то первый столбец передастся удачно, а дальше произойдет выход за границы массива. Дело в том, что MPI_Type_vector не учитывает смещение при индексировании. Грубо говоря, сейчас, когда мы передали первый столбец, переход ко второму начинается не смещением на sizeof(double), а на весь размер созданного типа данных, а это size (count) * size (stride) - начинаем передачу с конца массива матрицы.

Чтобы это исправить есть другая функция - MPI_Type_create_resized

int MPI_Type_create_resized(MPI_Datatype oldtype, 
                            MPI_Aint lb, 
                            MPI_Aint extent,
                            MPI_Datatype *newtype)

Она создает новый тип данных из исходного, но изменяет дельту при перемещении к следующему элементу. Чтобы исправить найденный недочет, создадим новый тип данных

MPI_Datatype columnType;
MPI_Type_create_resized(matrixColumnsType, 0, sizeof(double), &columnType);
MPI_Type_commit(&columnType);

Итоговая программа

#include <iostream>
#include <mpi.h>

double getLambda(double x, double y) {
    return 0.25 <= x && x <= 0.65 &&
    0.1 <= y && y <= 0.25 ? 0.01 : 0.0001;
}

double avg(double left, double right) {
    return (left + right) / 2;
}

void solveThomas(const double* F,
                    const double* lambda,
                    const int length,
                    const double min,
                    const double max,
                    const double step,
                    const double timeStep,
                    double* y) {
    const auto coefficient = 1.0 / (2 * step * step);

    double A[length], B[length], C[length];
    for (int i = 0; i < length; ++i) {
        A[i] = - avg(lambda[i + 1], lambda[i]) / 2 * coefficient;
        B[i] = - avg(lambda[i + 1], lambda[i + 2]) / 2 * coefficient;
        C[i] = 1 / timeStep - A[i] - B[i];
    }

    double alpha[length], beta[length];
    alpha[0] = alpha[length - 1] = 0;
    beta[0] = min;
    beta[length - 1] = max;

    for (int i = 0; i < length - 2; ++i) {
        alpha[i + 1] = - B[i + 1] / (C[i + 1] + A[i + 1] * alpha[i]);
        beta[i + 1] = (F[i + 1] - A[i + 1] * beta[i]) / (C[i + 1] + A[i + 1] * alpha[i]);
    }

    y[length - 1] = max;
    for (int i = length - 2; i >= 0; i--) {
        y[i] = alpha[i] * y[i + 1] + beta[i];
    }
}

void restoreF(const double* y,
              const double* lambda,
              const int size,
              const double step,
              const double timeStep,
              double* F) {
    const double coefficient = 1 / (2 * step * step);
    for (int i = 1; i < size - 1; ++i) {
        double lambdaPlusHalf = avg(lambda[i], lambda[i + 1]);
        double lambdaMinusHalf = avg(lambda[i], lambda[i - 1]);
        double temp = lambdaPlusHalf * (y[i + 1] - y[i]) - lambdaMinusHalf * (y[i] - y[i - 1]);
        F[i] = y[i] / timeStep + temp * coefficient;
    }
}

int main(int argc, char** argv) {
    const int size = 30;
    const int iterations = 3000;
    const double timeStep = 0.2;
    const double TxLeft = 600;
    const double TxRight = 1200;
    const double xStart = 0;
    const double xEnd = 1;
    const double yStart = 0;
    const double yEnd = 0.5;
    const double xStep = (xEnd - xStart) / size;
    const double yStep = (yEnd - yStart) / size;

    int processesCount, rank;
    
    double lambdaByX[size][size];
    double lambdaByY[size][size];

    for (int i = 0; i < size; ++i) {
        const double xValue = xStart + i * xStep;
        for (int j = 0; j < size; ++j) {
            const double yValue = yStart + j * yStep;
            double lambda = getLambda(xValue, yValue);
            lambdaByX[i][j] = lambda;
            lambdaByY[j][i] = lambda;
        }
    }

    MPI_Init(&argc, &argv);
    MPI_Comm_size(MPI_COMM_WORLD, &processesCount);
    MPI_Comm_rank(MPI_COMM_WORLD, &rank);
    if (processesCount != size) {
        if (rank == 0) {
            std::cout << "Количество процессов должно быть " << size << std::endl;
        }
        MPI_Finalize();
        return 0;
    }

    /// Создаем свой тип данных для передачи по столбцам
    MPI_Datatype matrixColumnsType, columnType;

    // Передача по столбцам
    MPI_Type_vector(size, 1, size, MPI_DOUBLE, &matrixColumnsType);
    MPI_Type_commit(&matrixColumnsType);

    // Перемещение по массиву делаем через каждые sizeof(double) байтов, т.е. смещение в 1 элемент
    MPI_Type_create_resized(matrixColumnsType, 0, sizeof(double), &columnType);
    MPI_Type_commit(&columnType);

    double* myLambdaX = lambdaByX[rank];
    double* myLambdaY = lambdaByY[rank];

    double temperatureReceive[size];
    double fReceive[size];

    if (rank == 0) {
        double temperature[size * size];
        double F[size * size];

        // Инициализируем начальные значения
        for (int i = 0; i < size; ++i) {
            for (int j = 0; j < size; ++j) {
                temperature[i * size + j] = 300;
                F[i * size + j] = 0;
            }
        }

        // Восстанавливаем первое значение F (F0)
        // Не по формуле - идем в другую сторону (восстанавливаем по X, а не по Y)
        for (int i = 0; i < size; ++i) {
            restoreF((temperature + i * size), lambdaByX[i], size, xStep, timeStep, (F + i * size));
        }

        for (int t = 0; t < iterations; ++t) {
            /// Вычисляю yn+1/2 и Fn+1/2
            MPI_Scatter(F, size, MPI_DOUBLE,
                        fReceive, size, MPI_DOUBLE,
                        0, MPI_COMM_WORLD);

            solveThomas(fReceive, myLambdaX, size, TxLeft, TxRight, xStep, timeStep, temperatureReceive);
            restoreF(temperatureReceive, myLambdaX, size, xStep, timeStep, fReceive);

            MPI_Gather(temperatureReceive, size, MPI_DOUBLE,
                       temperature, 1, columnType,
                       0, MPI_COMM_WORLD);
            MPI_Gather(fReceive, size, MPI_DOUBLE,
                       F, 1, columnType,
                       0, MPI_COMM_WORLD);


            /// Вычисляю yn+1 и Fn+1
            MPI_Scatter(temperature, 1, columnType,
                        temperatureReceive, size, MPI_DOUBLE,
                        0, MPI_COMM_WORLD);
            MPI_Scatter(F, 1, columnType,
                        fReceive, size, MPI_DOUBLE,
                        0, MPI_COMM_WORLD);

            solveThomas(fReceive, myLambdaX, size, TxLeft, TxRight, xStep, timeStep, temperatureReceive);
            restoreF(temperatureReceive, myLambdaX, size, xStep, timeStep, fReceive);

            // Аналогично принимаем только 1 элемент
            MPI_Gather(temperatureReceive, size, MPI_DOUBLE,
                       temperature, 1, columnType,
                       0, MPI_COMM_WORLD);
            MPI_Gather(fReceive, size, MPI_DOUBLE,
                       F, 1, columnType,
                       0, MPI_COMM_WORLD);
        }
      
        for (int i = 1; i < size - 1; ++i) {
          for (int j = 1; j < size - 1; ++j) {
              std::cout << temperature[i * size + j] << " ";
          }
          std::cout << "\n";
        }
      } else {
        for (int t = 0; t < iterations; ++t) {

            /// Вычисляю yn+1/2 и Fn+1/2
            // Получаю значения fReceive по X
            MPI_Scatter(fReceive, size, MPI_DOUBLE,
                        fReceive, size, MPI_DOUBLE,
                        0, MPI_COMM_WORLD);

            // Само вычисление
            solveThomas(fReceive, myLambdaX, size, TxLeft, TxRight, xStep, timeStep, temperatureReceive);
            restoreF(temperatureReceive, myLambdaX, size, xStep, timeStep, fReceive);

            // Возвращаю полученные данные
            MPI_Gather(temperatureReceive, size, MPI_DOUBLE,
                       nullptr, 0, MPI_DOUBLE,
                       0, MPI_COMM_WORLD);
            MPI_Gather(fReceive, size, MPI_DOUBLE,
                       nullptr, 0, MPI_DOUBLE,
                       0, MPI_COMM_WORLD);

            /// Вычисляю yn+1 и Fn+1
            // Получаю значения температуры и fReceive по Y
            MPI_Scatter(nullptr, 0, MPI_DOUBLE,
                        temperatureReceive, size, MPI_DOUBLE,
                        0, MPI_COMM_WORLD);
            MPI_Scatter(nullptr, 0, MPI_DOUBLE,
                        fReceive, size, MPI_DOUBLE,
                        0, MPI_COMM_WORLD);

            // Само вычисление
            solveThomas(fReceive, myLambdaY, size, TxLeft, TxRight, xStep, timeStep, temperatureReceive);
            restoreF(temperatureReceive, myLambdaY, size, xStep, timeStep, fReceive);

            // Возвращаю полученные значения
            MPI_Gather(temperatureReceive, size, MPI_DOUBLE,
                       nullptr, 0, MPI_DOUBLE,
                       0, MPI_COMM_WORLD);
            MPI_Gather(fReceive, size, MPI_DOUBLE,
                       nullptr, 0, MPI_DOUBLE,
                       0, MPI_COMM_WORLD);
        }
    }

    MPI_Type_free(&columnType);
    MPI_Type_free(&matrixColumnsType);

    MPI_Finalize();

}

Визуализация

Для визуализации логировались каждые 100 шагов из 3000 итераций с шагом 0.2. Результаты визуализированы с помощью matplotlib и seaborn

Полезные ссылки

https://ru.wikipedia.org/wiki/Уравнение_теплопроводности - Теория по задаче теплопроводности
https://algowiki-project.org/ru/Алгоритм_продольно-поперечной_прогонки - Объяснение алгоритма продольно-поперечной прогонки
https://github.com/ashenBlade/adi-mpi - Репозиторий с исходным кодом
https://stackoverflow.com/questions/10788180/sending-columns-of-a-matrix-using-mpi-scatter - Вопрос, который помог создать тип для отправки матрицы по столбцам

Комментарии (26)

Uranix
24.12.2022 13:52
#25042854
+6
А вы сравнивали, какое ускорение дает MPI версия? Я не вчитывался в код, но кажется что объем обменов и вычислений одного порядка, не понятно, почему вы пишете что задача CPU bound. Использование Scatter / Gather в вашем случае скорее всего убивает всю производительность.

Пример для 3D не удачный - ППП не применяют для 3D, так как она теряет свойство безусловной устойчивости.

Уравнение теплопроводности с переменным коэффициентом записывается как
$u_t = \mathrm{div}\, (\lambda \nabla u)$
В вашем случае нарушается условие непрерывности теплового потока через поверхность где коэффициент теплопроводности меняется. Но численный метод у вас как раз для правильной формы записан.
1. DistortNeo
  24.12.2022 17:47
  #25043308
  +1
  Да, в данном случае ускорение бы дало использование SIMD.
  Видимо, использование MPI было просто требованием к курсовой.
  1. Uranix
    24.12.2022 18:57
    #25043398
    На самом деле и прогонку можно распараллелить с помощью MPI. Просто это делается не тривиально.
    
    Pampam83
    24.12.2022 21:38
    #25043646
    +1
    Есть же PETSC.
    
    Andy_U
    24.12.2022 22:43
    #25043784
    А еще OpenFoam, Ansys, Fluent, Comsol, etc.
  1. rafuck
    24.12.2022 21:58
    #25043704
    Вообще говоря, MPI на SMP системе не сильно проиграет. На том же самом алгоритме крупнозернистого распараллеливания (не трогаем векторизацию и пр). До тех пор, пока сообщение помещается в кеш. Насколько я помню, на SMP-узлах основные реализации MPI через mm используют общую память для передачи сообщений, и потому, до тех пор, пока это сообщение помещается в кеш, разницы нет практически.
    
    Uranix
    25.12.2022 03:38
    #25044182
    И все равно делая Scatter / Gather на нулевой процесс каждый шаг, хорошего распараллеливания не получить
1. rafuck
  24.12.2022 22:00
  #25043712
  То же самое можно написать интегральным тождеством. Построить ортогональную сетку, каждый четырехугольник согласованно с остальными разбить на два треугольника (с сохранением конформности), применить МКЭ на полилинейном базисе и получить то же самое.
  1. rafuck
    24.12.2022 22:32
    #25043768
    +2
    Отмечу еще, что в реальности нет никакой константы теплопроводности для материала, да и плотности, впрочем. Они зависят от температуры и, еще более существенно, - от агрегатного состояния вещества. Но это неважно в данном контексте ,)

belch84
24.12.2022 14:40
#25042950
+8
Недавно хотел применить уравнение теплопроводности для объяснения факта, который заметил в процессе приготовления оладьев (посмотрел, что нужно писать «оладий», но в такой форме слово меня раздражает) специального вида. Речь об оладьях с яблоками, которые получаются, когда целое яблочное кольцо (цилиндр с дыркой) окунается в тесто и поджаривается
Оладьи с яблоками, исходные материалы

Обнаружилось, что у таких оладьев серединка пропекается недостаточно, тесто там остается сырым
Оладьи с яблоками, непропеченная серединка

Хотелось свести объяснение к решению краевой задачи для обыкновенного дифференциального уравнения, но не получилось, а более сложные методы использовать было лень. Понятно, что решать нужно в цилиндрических координатах и что решения — это функции Бесселя. Понятно также, что теплопроводность у яблока и теста разная, хотя, возможно, даже без яблока серединка пропекается хуже, чем края
1. vassabi
  24.12.2022 16:01
  #25043126
  +2
  я думаю что это не только теплопроводность и теплоемкость, но и наличие избытка воды в яблоке. Вы не пробовали резать их на тонкие кольца, подсушивать, а потом печь оладьи из сушеных колец ?
  1. belch84
    24.12.2022 16:07
    #25043148
    Не пробовал, этот вид оладьев и так достаточно трудоёмкий в изготовлении. Тем не менее, оставлять тесто сырым тоже не хочется, поэтому приходится проковыривать дырочку в уже прожаренной стороне, немного выжимать сырое тесто, а затем снова переворачивать на уже прожаренную сторону, получается что-то вроде «заплатки» в центре
    
    vassabi
    24.12.2022 19:35
    #25043452
    у меня мама делает оладьи с яблоками - но она режет их на тонкие (почти прозрачные) дольки и перемешивает с тестом. тесто запекается отлично.
    
    Или вам важно, чтобы они были именно такой формы ?
    
    belch84
    24.12.2022 21:25
    #25043630
    +1
    Я не очень большой специалист по именно оладьям. Естественно, есть несколько разных вариантов приготовления оладьев с яблоками. Можно, например, яблоко просто потереть на терке и добавить в тесто, но так можно и не догадаться, что в оладьях есть яблоки (проводил эксперимент и опрос среди родственников). Рецепт с дисками мне нравится тем, что в нём яблоко чувствуется явно и при этом не раскисает.
1. Uranix
  24.12.2022 16:03
  #25043132
  +2
  Кажется, что единственный вариант, при котором уравнение теплопроводности может объяснить эффект - это если температуропроводность яблок сильно выше температуропроводности теста. Тогда яблоко "втягивает" в себя линии тока тепла, прямо как ферромагнетик втягивает в себя линии напряженности магнитного поля.
  
  Другая гипотеза - что яблоко представляет собой по большей части воду, из-за чего нагреть его выше 100С становится проблематично вплоть до состояния, когда большая часть воды испарится / свяжется с чем-то. А тесту такой температуры недостаточно для застывания, вот тесто вблизи яблок не пропекается.
  
  Но возможно тут существенен еще переход теста из жидкого состояния в твердое с изменением физических характеристик, тогда это уже ближе к задаче Стефана.
  
  Возможно, перенос тепла теплопроводностью сильно хуже переноса тепла конвекцией горячего воздуха вокруг оладьев, это могло бы объяснить, почему центр не пропекается. Но тогда яблоки совсем не при чем.
  1. rafuck
    24.12.2022 22:09
    #25043732
    А в тесте нет воды?
    
    vassabi
    25.12.2022 03:42
    #25044186
    есть, но ИМХО - значительно меньше чем в свежем яблоке

Un_ka
24.12.2022 15:15
#25043016
+1
Осталось дело за малом и conjugate heat transfer можно будет решать. ;)

Сетка ортогональная? График сходимости не строили?
1. AshBlade Автор
  24.12.2022 15:16
  #25043018
  Сетка ортогональная. График сходимости не строил

Andy_U
24.12.2022 16:25
#25043184
+1
Вопрос, Вам нужно было задачу решить или написать что-то типа курсовой работы, диплома, etc.?
1. AshBlade Автор
  24.12.2022 16:26
  #25043188
  Что-то типа курсовой работы
  1. Andy_U
    24.12.2022 16:42
    #25043214
    А метод решения был задан?
    
    AshBlade Автор
    24.12.2022 16:47
    #25043226
    Метод продольно-поперечной прогонки с неявной схемой

Anton_Menshov
24.12.2022 20:37
#25043540
+1
Данная задача не CPU-bound, а memory-bandwidth bound. И, частично, эта проблема может решаеться путем использования MPI и работе на нескольких кластерах. Однако, это не делает ее CPU-bound. Больший эффект при меньших ресурсах даст увеличение локальности данных и оптимизация порядка доступа в кэш\память.

Однако, если задачей было, распараллеливая через MPI, написать код для теплопроводности - отл.

rafuck
24.12.2022 22:14
#25043744
+1
В этой схеме расщепления по-хорошему, надо еще поитерировать на одном временном слое. Вообще, в докладах Нижегородского университета одно время часто возникала их метод распараллеливания прогонки (в том числе для блочно-диагональных матриц). Нашел ссылку на методичку. Стр. 13 http://www.unn.ru/pages/e-library/methodmaterial/files/9.pdf
1. XTBZ
  27.12.2022 06:29
  #25050150
  К.Р.Ф., отличная методичка, вовремя, как раз хотел что-то такое поискать, спасибо!

Задача теплопроводности методом продольно-поперечной прогонки средствами MPI +10

Постановка задачи

Продольно-поперечная прогонка

Метод прогонки

Последовательное решение

Параллельная реализация

Итоговая программа

Визуализация

Полезные ссылки

Комментарии (26)

AshBlade Автор

AshBlade Автор

AshBlade Автор