Меня искренне восхищает то, как Крис Бернхардт рассказывает про квантовые вычисления в своей книге. На мой дилетантский взгляд, объяснение неравенства Белла в его исполнении – лучшее, что можно найти сейчас в интернете без доступа к телу кафедры квантовой физики. Я бы хотел пересказать его изложение, так что если вы уже читаете книгу – смело пропускайте эту статью.
Введение
Вам же знакомо выражение "Бог не играет в кости"? В основе квантовой физики лежит принятие вероятности как факта: принципиально невозможно провести измерение с бесконечной точностью – можно лишь вычислить вероятность наступления того или иного события. Впрочем, наблюдать такие эффекты можно лишь в микромире.
Классическая же физика опирается на прямо противоположное утверждение: если все параметры и законы природы заранее известны, то результат взаимодействия объектов можно вычислить с бесконечной точностью. Вычисления с использованием вероятности играют роль всего лишь удобного инструмента, который достаточно прост и обладает удовлетворительной точностью, как пример – термодинамика.
Подобные споры наука всегда решает один-единственным способом – с помощью проведения эксперимента. Стоит отметить, что наука не ставит себе целью ответить на вопросы "Почему?" и "Что?": мы понятия не имеем, что такое электрон или почему он существует. Наука строит модель реальности, позволяя её описать, а также предсказать результаты взаимодействия: хоть мы и не знаем, что такое электрон, мы можем описать его взаимодействие с электрическим полем. Как же поставить такой эксперимент, который подтвердил бы правоту классического или квантового подхода? Тут нам на помощь и приходит неравенство Белла.

Представим, что у Алисы и Боба есть пачка запутанных кубитов:

Алиса и Боб измеряют эти кубиты в 3 разных ортогональных базисах: A, B и C.
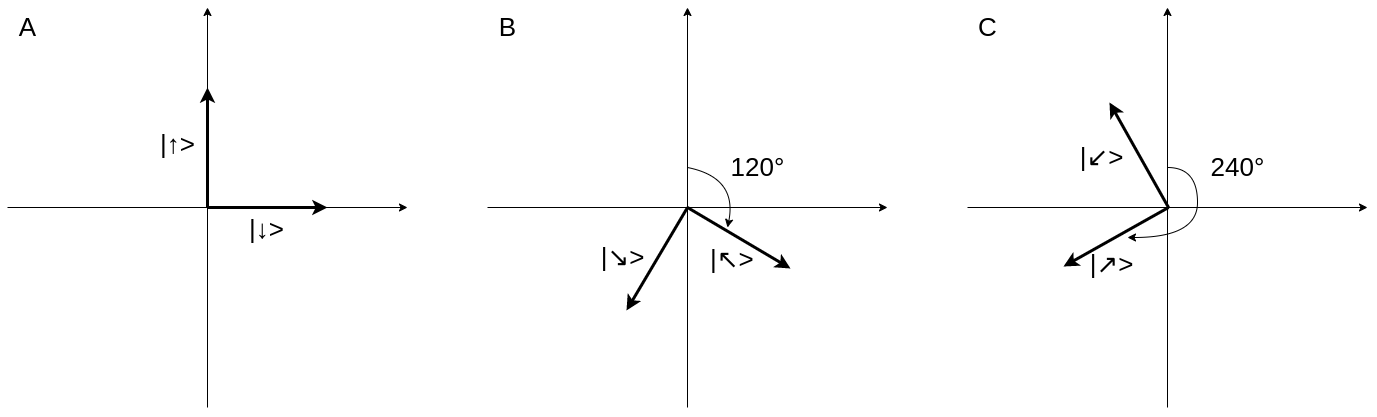
Несложно заметить, что базис B получен с помощью поворота базиса A на 120°, а базис C – поворотом на 240°. Первый вектор в базисе соответствует бинарному 0, а второй – бинарной 1. Алиса и Боб выбирают базис для измерения случайным образом и независимо друг от друга. Внимание, вопрос: какова вероятность того, что Алиса и Боб получат одинаковый результат измерения?
Квантовое решение
Известно, что в случае одинаковых базисов Алиса и Боб гарантированно получают одинаковый результат. Поскольку базисов 3, то вероятность такого выбора – 1/3. Для того, чтобы понять, как изменится результат при разных базисах, покрутим их, стряхнув перхоть пыль с тригонометрии:
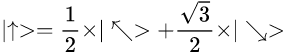
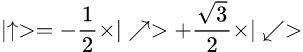
Получается следующее: если Алиса выберет базис А, Боб – базис B, то вероятность получить одинаковый результат (векторы выше – для результата 0 у Алисы) в качестве измерения равна 1/4; то же справедливо и для A,C.
Посчитаем теперь вероятность получить одинаковый результат при измерении:
(1/3 × 1) + 2/3 × 1/4 = 1/3 + 1/6 = 1/2Согласно квантовой теории, Алиса и Боб получают одинаковый результат измерений с вероятностью 1/2.
Классическое решение
С точки зрения классической физики вероятности не существует, а результат измерений зависит от конфигурации системы кубитов. Используем нотацию XYZ для описания системы:
X – результат измерения кубитов в базисе A;
Y – результат измерения кубитов в базисе B;
Z – результат измерения кубитов в базисе C.
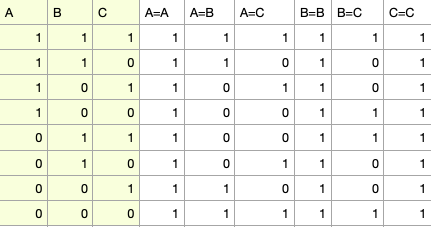
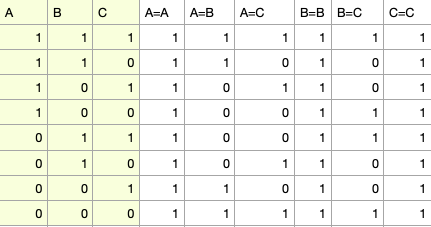
Переберём все возможные варианты. '+' означает одинаковый результат измерения, '-' – разный.
A,A |
A,B |
A,C |
B,A |
B,B |
B,C |
C,A |
C,B |
C,C |
|
000 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
001 |
+ |
+ |
- |
+ |
+ |
- |
- |
- |
+ |
010 |
+ |
- |
+ |
- |
+ |
- |
+ |
- |
+ |
011 |
+ |
- |
- |
- |
+ |
+ |
- |
+ |
+ |
100 |
+ |
- |
- |
- |
+ |
+ |
- |
+ |
+ |
101 |
+ |
- |
+ |
- |
+ |
- |
+ |
- |
+ |
110 |
+ |
+ |
- |
+ |
+ |
- |
- |
- |
+ |
111 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
Заметим, что в каждой строке как минимум по 5 '+'. Это означает, что для любой конфигурации кубитов вероятность получить одинаковый результат при измерении – не меньше 5/9, значит, общая вероятность получить одинаковый результат – не меньше 5/9.
Неравенство
Неравенство Белла позволяет экспериментально выяснить, какая же теория верно описывает кубиты – классическая или квантовая: если на большом количестве измерений число совпадений равно 1/2 – права квантовая теория, если же совпадают 5/9 измерений – верен классический подход. Несложно догадаться, что провести такой эксперимент в родительском гараже нельзя, да и вообще, запутывание кубитов – отдельный вид искусства. Впрочем, умные люди уже реализовали несколько экспериментов с разной точностью и допущениями, каждый из которых подтвердил именно квантовую теория (ура, я не зря читал эту книжку).
Протокол E91
Артур Экерт предложил протокол получения общего ключа, который опирается на неравенство Белла – протокол E91. Если вы знакомы с BB84, вас порадует наличие общих элементов у двух протоколов.
Алиса и Боб получают поток запутанных кубитов и используют 3 разных базиса для измерения – всё ровно так, как мы только что обсудили. Если Алиса и Боб используют одинаковый базис для измерения, они гарантированно получают одинаковый результат. Спустя достаточно большое число измерений у Алисы и Боба оказывается в распоряжении строка совпадающих битов длиной 1/3 от общей передачи. Алиса и Боб могут определить совпадающие биты, переслав друг другу список использованных базисов по открытому каналу:
Alice:
B C B C A A B C B
A B A C A B B A C
Bob:В примере выше совпадают позиции 4,5,7, поэтому соответствующие биты можно было бы использовать как общий ключ. Однако Ева иногда подслушивает, поэтому перед использованием ключа нужно провести дополнительную проверку.
Нам известно, что, согласно объяснению неравенству Белла, вероятность получить одинаковый результат при разных базисах равен 1/4, если кубиты запутаны. Что меняется, когда Ева перехватывает эти кубиты? Тут я приведу перевод ответа Фрэнка Йеллина:
Предположим, что Ева так же, как Алиса и Боб, выбирает базис случайным образом. Нам известно, что Алиса и Боб выбрали разные базисы. Вероятность того, что Ева выберет какой-то из этих двух базисов – 2/3, а вероятность того, что все три базиса разные – 1/3.
Если Ева выбирает базис Алисы или Боба, то шанс получить одинаковый результат не меняется, оставаясь равным 1/4.
Что же происходит, когда Ева выбирает оставшийся базис? Она проводит своё измерение, распутывая кубиты, но копируя их состояние. Теперь Алиса измеряет свой кубит. Вероятность того, что она получит результат, отличный от измерения Евы – 3/4, а шанс получить одинаковый результат – 1/4. То же справедливо для Боба. Таким образом, вероятность для Алисы и Боба получить одинаковый результат измерения:
3/4 × 3/4 + 1/4 × 1/4 = 5/8
Сложив все случаи, получим следующее: 2/3 × 1/4 + 1/3 × 5/8 = 3/8
Вот мы и получили способ выяснить, подслушивает Ева или нет:
если измерения с разным базисом совпадают в половине случаев, то можно спокойно использовать полученный ключ;
если же частота совпадения составляет 0.375, кто-то активно прослушивает канал, поэтому полученный ключ использовать небезопасно.
Спасибо за рецензию: Анастасии Куралёвой
Канал в Телеграме: https://t.me/networking_it_ru
Комментарии (64)

sbars
00.00.0000 00:00Вот всегда было интересно, а откуда "первый кубит", "второй кубит", если кубиты реализованы одинаковыми частицами, а они неразличимы?
Как можно говорить об отдельных состояниях частиц в паре, если не известно, где какая?

braonle Автор
00.00.0000 00:00Ну Вы же можете их как-то пронумеровать? В примере выше кубиты запутаны одинаково (например, преобразованием Адамара), так что нет разницы, какой считать первым или вторым. Фокус в том, что это сугубо обозначение.
Когда кубиты в одинаковом состоянии уже пронумерованы, вы их и различаете по этому номеру, впоследствии преобразуя разными способами таким образом, чтобы измерение одного из них (любого!) давало нужный результат. Мне кажется, наглядный пример такого подхода - алгоритм Дойча.

michael_v89
00.00.0000 00:00Алиса и Боб измеряют эти кубиты в 3 разных ортогональных базисах: A, B и C.
Первый вектор в базисе соответствует бинарному 0, а второй – бинарной 1.Как соотносится некий "базис" с реальными физическими величинами — ориентация прибора и ориентация поляризации/спина квантовой частицы?
Почему 0 и 1 ортогональны? Если один спин вверх, то другой спин вниз, это 2 противоположных направления на одной прямой.
braonle Автор
00.00.0000 00:00Вот про спин ответить не смогу, не знаю. С поляризацией света попроще, там двумерный базис можно собрать из перпендикулярных светофильтров.
Ортогональны не 0 и 1, а (1,0) и (0,1). Поскольку события два, то и базисных векторов два. Если бы были возможны 3 независимых события, то векторы были бы трехмерными. Замечу, что ортогональны не значения спина (они так-то скалярные), а базисные вектора в модели, описывающей состояние частицы.
michael_v89
00.00.0000 00:00А что означают цифры в таблице? У нас же 2 кубита, почему там 3 цифры с результатом 0/1?

braonle Автор
00.00.0000 00:00Как и написано в тексте, это варианты состояния системы с точки зрения классической физики. Первая цифра - результат измерения в первом базисе, вторая - во втором. 010 означает, что в базисе А измерение даст 0, в базисе В - 1, в базисе С - 0.

michael_v89
00.00.0000 00:00Это выглядит неправильно. Результаты в разных базисах же не независимы, предполагается, что это один и тот же фотон. Если повернуть измерительный прибор не на 120 градусов, а на 180, результаты будут полностью противоположны, комбинации 00 никогда не будет. Мне кажется, если посчитать с учетом этого, то тоже получится 1/2.

braonle Автор
00.00.0000 00:00Почему один фотон? Два связанных фотона, которые образуют некую систему. В трех базисах у такой системы могут быть 8 состояний.
Так на 180 и не надо поворачивать. Задача - найти способ экспериментально проверить, какой подход, классический или квантовый, прав, а для этого нужны разные предсказания. Ну получите вы 1/2 в обоих случаях, и что? Поворот на 120 и даёт способ получить разные предсказания двух моделей, а затем проверить их экспериментально.

michael_v89
00.00.0000 00:003 цифры это же результат измерения одного фотона в базисах A, B, C.
Так на 180 и не надо поворачивать.
Это не вопрос, надо или не надо, это просто факт) Результаты в разных базисах не независимы, поэтому все возможные комбинации 0 и 1 перебирать нельзя. Или можно, но они будут не равновероятные.
Ну получите вы 1/2 в обоих случаях, и что?
1/2 это то, что получилось для квантового решения, а не вероятности одного измерения. Я говорю, что если учитывать, что результаты в разных базисах не являются независимыми, то предположительно получится такой же результат, как и для квантового решения.

Shkaff
00.00.0000 00:001 в таблице значит, что результаты измерения двух кубитов совпали, а 0 - что не совпали.

michael_v89
00.00.0000 00:00Cовпадение же обозначается знаком '+' в таблице.

michael_v89
00.00.0000 00:00То есть если построить такую же таблицу для 2 базисов, повернутых на 180°, то получится, что вероятность получить одинаковые результаты не меньше 1/2, хотя на самом деле она 0.

Shkaff
00.00.0000 00:00+2Упс, это я перепутал, прошу прощения.
Тогда я не очень понимаю, про какие корреляции идет речь. Классический случай == заранее заданное с абсолютной точностью состояние еще до начала измерения. Т.е. вы готовите состояние 11 и состояние 00 в 50 процентах случаев, но оно задано уже в момент измерения. Дальше просто считаете, какие будут варианты исхода измерения в этом случае.
Мне кажется, табличка просто не очень удачная. Запишите все варианты для результатов измерения A, B, C независимо, а потом посмотрите на совпадения.
Дальше посчитайте вероятность совпадения. В 1/3 случаев вы получаете одинаковые результаты, т.к. базисы совпадают. В остальных 2/3 случаев вы получаете совпадение в 1/3 результатов. Предполагая, что базисы выбираются случайно, вы получаете вероятность совпадения 1/3 + 2/3*1/3 = 5/9.
PS Мне нравится другой вариант доказательства теоремы Белла, я про него писал в отдельной статье тут. Там все еще более на пальцах.

michael_v89
00.00.0000 00:00Так я и говорю, строки в таблице нельзя считать равновероятными. Представьте, что A, B, C отличаются всего на 1 градус. Таблица комбинаций будет такая же, но фактические результаты другие, совпадение будет в 99% случаев.

Shkaff
00.00.0000 00:00Нет, почему? Мы вообще не считает частоту выпадения конкретного результата, а совпадения между двумя станциями измерения. Нам не важно, какой базис там, главное иметь три разных.

nik123123
00.00.0000 00:00мне вот тоже кажется вы правы
хотя и уверен что это не верно (все таки неравенство не глупые люди придумали)

michael_v89
00.00.0000 00:00А что конкретно измеряют Алиса и Боб? Алиса первый запутанный кубит, а Боб второй, или они оба в разных экспериментах измеряют какой-то один кубит, а второй игнорируют?

Shkaff
00.00.0000 00:00Алиса первый кубит, Боб - второй. Оба измерения независимы и случайным образом выбирают базис (из трех).

michael_v89
00.00.0000 00:00То есть там делается поправка для второго кубита, и его результаты инвертируются? Если мы просто измерим первый кубит в базисе A, и второй в базисе A, то их результаты будут противоположными, а не одинаковыми — у одного спин вверх, у другого вниз.

Shkaff
00.00.0000 00:00Кубиты изначально приготовлены в состоянии ↑↑ + ↓↓, т.е. если у одно спин вниз - у другого тоже.

michael_v89
00.00.0000 00:00А что означают коэффициенты в первой формуле в статье? Равная вероятность получить как оба вверх, так и оба вниз, и нулевая получить разные результаты?

michael_v89
00.00.0000 00:00А подскажите пожалуйста еще насчет установки. Допустим, если это фотоны, и мы проверяем вертикальную/горизонтальную поляризацию, наклон угла поляризации у испускаемых фотонов может быть произвольный, или они подготавливаются определенным образом, чтобы он был например строго "0 либо 90°" относительно вертикали?

michael_v89
00.00.0000 00:00braonle Shkaff
Получил результат 1/2 со скрытыми параметрами.Идея.
Меряем поляризацию фотона, прошел через прибор либо нет.
На прохождение влияет не только фаза, но и амплитуда E в момент подлета фотона к прибору. Если углы поляризации фотона и ориентации прибора совпадают, проходит любая амплитуда. Если отличаются, большая амплитуда заденет материал поляризационной решетки, и произойдет отражение, маленькая не заденет, и фотон пройдет через прибор.
Чем больше разность углов, тем меньше должна быть амплитуда для прохождения. Для 90 градусов отражение будет всегда (2 поляризатора под прямым углом).Амплитуда в момент подлета имеет свойства случайной величины, но при этом полностью зависит от начальных факторов. Например расстояние от испускающей установки до приборов, тепловое движение молекул измерительного прибора. Ну или можно представить, что начальная фаза не 0, а имеет произвольное значение (в зависимости от окружающих факторов).
Может быть играет роль не фаза, а какой-то другой скрытый параметр, который влияет на отражение, который связан с неизвестным полем или 4 измерением. Он выбирается произвольным образом в момент создания фотона, но влияет на результат измерения в момент измерения.В скрипте углы поделены на 2, так как для поляризации нет разницы 0 или 180, это все равно вертикальная поляризация.
Код(function() { /* Bell inequality, 1/2 with hidden parameters. Idea: Photon has some relatively random phase offset when it comes to device. It depends on distance to devices, heat motion of the device material, heat motion of sending device, etc. So it has some random amplitude at this point. But it depends only on starting conditions. When polarization angle and device angle don't match, maximum amplitude touches the device material and causes reflection. Only small amplitude can pass through the gap in device. The bigger angle is between device and polarization - the smaller amplitude is allowed to pass through. Maybe it's not a phase but some other hidden parameter from 4th dimention which has random initial value and affects the reflection. */ let basisA = toRadians(0), basisB = toRadians(60), basisC = toRadians(120); let allBasises = [basisA, basisB, basisC]; let resultPass = 1, resultReflect = 0; run(); return; function run() { let matchCount = 0, notMatchCount = 0, totalCount = 1000; for (let i = 0; i < totalCount; i++) { let photon = createPhoton(); let [resultAlice, resultBob] = oneRun(photon); if (resultAlice === resultBob) { matchCount++; } else { notMatchCount++; } } console.log(matchCount, notMatchCount, totalCount); } function rand(max) { return Math.random() * max; } function toRadians(degree) { return Math.PI * degree / 180; } function createPhoton() { let polarizationDegree = rand(toRadians(180)); return { polarizationDegree: polarizationDegree }; } function oneRun(photon) { let phaseOffsetAtDeviceAlice = Math.random() * 2*Math.PI; let phaseOffsetAtDeviceBob = Math.random() * 2*Math.PI; let basisAlice = allBasises[parseInt(rand(3))]; let basisBob = allBasises[parseInt(rand(3))]; let resultAlice = calcResult(photon, phaseOffsetAtDeviceAlice, basisAlice); let resultBob = calcResult(photon, phaseOffsetAtDeviceBob, basisBob); return [resultAlice, resultBob]; } function calcResult(photon, phaseOffsetAtDevice, basis) { let eAmplitudeAtDevice = Math.abs(Math.sin(phaseOffsetAtDevice)); let polarizationDiff = Math.abs(photon.polarizationDegree - basis); let maxAllowedEAmplitudeAtDevice = Math.abs(Math.cos(polarizationDiff)); let result; if (eAmplitudeAtDevice < maxAllowedEAmplitudeAtDevice) { result = resultPass; } else { result = resultReflect; } return result; } })()

Shkaff
00.00.0000 00:00Если отличаются, большая амплитуда заденет материал поляризационной
решетки, и произойдет отражение, маленькая не заденет, и фотон пройдет
через прибор.Я вот этого не понял, это как работает? Вообще, что вы понимаете под амплитудой фотона? Амплитуда и фаза, о которых обычно идет речь - у волновой функции, но у вас не может быть инструмента, который реагирует на амплитуду ВФ как-то.

michael_v89
00.00.0000 00:00Насколько я знаю, под направлением поляризации обычно понимают направление вектора E, амплитуда это его длина.

Shkaff
00.00.0000 00:00Но в квантовой механике поле одиночного фотона не определено.
Более того, если у вас как-то есть прибор, который умеет различать амплитуды поля, он неизбежно будет также запутываться с фотоном (другими словами, любая статистика на выходе из такого "поляризатора" будет неизбежно испорчена).

michael_v89
00.00.0000 00:00В общем-то неважно, что это за параметр, важно что можно его задавать при создании фотона и получить результат 1/2 в этом эксперименте.

Shkaff
00.00.0000 00:00Я не знаю, как вы получаете это, код я разбирать не очень хочу, но у вас точно ошибка, потому что именно так выглядят скрытые переменные. Результат для неравенства Белла для них - строгий математический вывод.

michael_v89
00.00.0000 00:00если у вас как-то есть прибор, который умеет различать амплитуды поля
Прибор не измеряет амплитуду, он измеряет только прошел фотон через поляризатор или отразился. Амплитуду "измеряет" Вселенная, когда фотон взаимодействует с решеткой. Каким-то же образом отражение происходит, есть какие-то физические законы, которые действуют при взаимодействии фотона и решетки.
потому что именно так выглядят скрытые переменные
Ну так я про это и говорю. У меня есть скрытые переменные, которые задаются при создании фотона, или определяются условиями в момент его возникновения, и результат получается 1/2.
В общем-то математически нет никакой разницы, когда мы задаем случайную величину — при создании частицы или в момент измерения, если она играет роль только в момент измерения.
Результат для неравенства Белла для них — строгий математический вывод
А у меня строгая воспроизводимая программа со скрытыми параметрами)
Таблица в статье составлена для одной величины "спин", а у меня есть второй псевдослучайный параметр "амплитуда в момент подлета", который влияет на отражение. В первом варианте я сделал одну случайную величину, и там конечно были результаты как в таблице.

Shkaff
00.00.0000 00:00Амплитуду "измеряет" Вселенная, когда фотон взаимодействует с решеткой.
Если фотон взаимодействует с решеткой так, что пропускание зависит от его амплитуды (или какого-то другого параметра), у вас обязательно происходит запутывание и дальнейшая статистика не имеет смысла.
А у меня строгая воспроизводимая программа со скрытыми параметрами)
Значит, в ней ошибка (или еще где-то).

Shkaff
00.00.0000 00:00В общем-то математически нет никакой разницы, когда мы задаем случайную величину — при создании частицы или в момент измерения, если она играет роль только в момент измерения.
Так о том и речь, что есть разница. Неравенства Белла именно про это.

michael_v89
00.00.0000 00:00Речь как раз о том, что нет. Неравенства Белла про одну величину, а у меня их 2. Разберите программу все-таки.

Shkaff
00.00.0000 00:00Я пока не понимаю даже вашей предпосылки (явно амплитуда это не то, о чем можно осмысленно говорить).

michael_v89
00.00.0000 00:00Ок, тогда для начала ответьте на вопрос, как происходит отражение фотона, от чего это зависит. Хотя бы себе, а не в комментах. Потом подумайте, от чего зависит их частичное прохождение через поляризационную решетку при разнице углов между 2 поляризаторами в 45 градусов. Чем ближе угол к 90, тем меньше фотонов проходит. Вот у меня в программе используется причина этого уменьшающегося количества проходящих фотонов.
пропускание зависит от его амплитуды (или какого-то другого параметра)
Пропускание в любом случае от чего-то зависит, так как мы наблюдаем разные результаты, иногда запутанный фотон проходит, иногда нет.
Но в квантовой механике поле одиночного фотона не определено.
На Вселенную никак не влияет что мы там где определяем. Фотон не может существовать без колебаний электромагнитного поля. Если есть фотон, значит есть ненулевые значения электрического и магнитного полей, даже если мы в рамках какой-то науки их не рассматриваем.
явно амплитуда это не то, о чем можно осмысленно говорить
Ну как это, вектора напряженности E и B это вполне осмысленные физические величины.
В общем-то математически нет никакой разницы, когда мы задаем случайную величину — при создании частицы или в момент измерения
Тут признаю, я поторопился, это не так, но это ничего не меняет. Программа работает по-другому. Там моделируется псевдослучайная величина, зависящая от окружающих факторов. Например тепловое движение молекул в приборах, от которого зависит величина E в момент взаимодействия с прибором, от чего зависит, пройдет фотон или нет.

Shkaff
00.00.0000 00:00Ну как это, вектора напряженности E и B это вполне осмысленные физические величины.
Для непрерывного поля, но не для одиночного фотона. Если вы рассматриваете напряженности поля - не имеет смысла говорить об одиночных фотонах. Если рассматриваете поле, то вам и эксперимент для него надо проводить. Сейчас вы смешали разные понятия из разных частей.
Вот у меня в программе используется причина этого уменьшающегося количества проходящих фотонов.
Этого я не понимаю. Допустим, у вас есть скрытая переменная, которая задает, по какому пути должен пойти фотон на поляризаторе. Без проблем, но в таком случае эта переменная должна влиять на оба поляризатора у Алисы и Боба, которые разнесены в пространстве-времени. Такая скрытая переменная - нелокальная, и на нее неравенство Белла не распространяется (это в целом хорошо известный факт и используется в разных интерпретациях КМ).

michael_v89
00.00.0000 00:00Если вы рассматриваете напряженности поля — не имеет смысла говорить об одиночных фотонах.
Квантовые поляризационные состояния фотонов
Ну вот здесь говорится и про поляризацию фотона и про вектор E.
Без проблем, но в таком случае эта переменная должна влиять на оба поляризатора у Алисы и Боба
Такая скрытая переменная — нелокальнаяПочему, первый фотон на устройство Алисы попадет с одной фазой, второй фотон на устройство Боба с другой, и в разных экспериментах из-за теплового движения молекул эти значения будут разные. Положение молекул измерительного прибора это локальная переменная.
Или вот, немного переделал скрипт, теперь там используется абстрактный hiddenParameter, который влияет на отражение, и его значение генерируется при создании запутанных фотонов. Просто у обоих фотонов оно разное. Но при этом это локальное свойство фотонов.
Код(function() { let basisA = toRadians(0), basisB = toRadians(60), basisC = toRadians(120); let allBasises = [basisA, basisB, basisC]; let resultPass = 1, resultReflect = 0; run(); return; function run() { let matchCount = 0, notMatchCount = 0, totalCount = 1000; for (let i = 0; i < totalCount; i++) { let [photon1, photon2] = create2EntangledPhotons(); let [resultAlice, resultBob] = oneRun(photon1, photon2); if (resultAlice === resultBob) { matchCount++; } else { notMatchCount++; } } console.log(matchCount, notMatchCount, totalCount); } function rand(max) { return Math.random() * max; } function toRadians(degree) { return Math.PI * degree / 180; } function create2EntangledPhotons() { let polarizationDegree = rand(toRadians(180)); let hiddenParameterPhoton1 = rand(toRadians(360)); let hiddenParameterPhoton2 = rand(toRadians(360)); let photon1 = { polarizationDegree: polarizationDegree, hiddenParameter: hiddenParameterPhoton1 }; let photon2 = { polarizationDegree: polarizationDegree, hiddenParameter: hiddenParameterPhoton2 }; return [photon1, photon2]; } function oneRun(photon1, photon2) { let basisAlice = allBasises[parseInt(rand(3))]; let basisBob = allBasises[parseInt(rand(3))]; let resultAlice = calcResult(photon1, basisAlice); let resultBob = calcResult(photon2, basisBob); return [resultAlice, resultBob]; } function calcResult(photon, basis) { let smallAngle = Math.abs(photon.polarizationDegree - basis) < 45; let shouldPass = (photon.hiddenParameter < toRadians(360 / 2)); let result; if (smallAngle && shouldPass) { result = resultPass; } else { result = resultReflect; } return result; } })()

Shkaff
00.00.0000 00:00Квантовые поляризационные состояния фотонов
Ну вот здесь говорится и про поляризацию фотона и про вектор E.
Ну вот там буквально: "Для квантового описания единичного фотона мы можем абстрагироваться от абсолютных значений E1 и E2, важен лишь вид той винтовой линии, которую описывает в пространстве вектор E." Для одиночного фотона амплитуда поля Е не задана.
Почему, первый фотон на устройство Алисы попадет с одной фазой, второй фотон на устройство Боба с другой
При чем тут фаза вообще? Или вы про направление поляризации?
Положение молекул измерительного прибора это локальная переменная.
Ну, во-первых, как я уже писал выше, никакое из реального физического воздействия не может выступать в такой роли: если положение молекул как-то влияет на отражение, фотон оказывается запутан с этими молекулами и вы увидите на выходе просто тепловое состояние без каких-либо корреляций. Очевидно, вы этого не учитываете.
Так что это должна быть реально скрытая переменная - некий параметр, который не является частью нашего обычного мира. Если он создается в момент создания фотонов и "знает" о "настоящем" состоянии фотона, то в таком случае он не отличается от обычных скрытых параметров, так что нет причин полагать, что это будет влиять на исход эксперимента. До тех пор, пока вы можете выбирать измерительный базис как хотите, это не будет влиять. Если скрытые переменные влияют на выбор базиса, это уже называется супердетерминизм:)

michael_v89
00.00.0000 00:00линии, которую описывает в пространстве вектор E." Для одиночного фотона амплитуда поля Е не задана.
Если вектор есть, значит и длина у него есть, это и есть амплитуда. Понятие "описывает" относится к концу вектора, от центральной точки до конца вектора и есть длина.
При чем тут фаза вообще? Или вы про направление поляризации?
Я про значение амплитуды вектора Е. При плоской поляризации оно меняется по синусоиде, точка пересечения синусоиды с материалом прибора происходит в некоторой фазе этой синусоиды.
фотон оказывается запутан с этими молекулами
Так я же как раз привожу пример со скрытыми переменными, которые работают без какой-то особой запутанности.
вы увидите на выходе просто тепловое состояние без каких-либо корреляций
Ну вот, этот тепловой шум как раз и проявляется в случайности при измерении поляризации фотона.
нет причин полагать, что это будет влиять на исход эксперимента
Будет, если его значение разное для разных фотонов из пары. Не уверен, что такая ситуация возможна с реальными параметрами, но в рамках абстрактной модели в программе это работает.
Ну и также будет когда случайность вносит измерительный прибор, как в примере с молекулами. В принципе это можно проверить экспериментально, провести эксперимент при низких температурах и для фотона с большой длиной волны порядка сантиметров или метров.

michael_v89
00.00.0000 00:00В принципе это можно проверить экспериментально, провести эксперимент при низких температурах
Нашел исследование в интернете. Всё не читал, но вроде пишут, что при низкой температуре есть нарушение неравенства, которое уходит с повышением температуры.
Temperature Dependence of Violation of Bell's Inequality in Coupled Quantum Dots in a Microcavity
"Bell's inequality in two coupled quantum dots within cavity QED, including Forster and exciton-phonon interactions, is investigated theoretically. It is shown that the environmental temperature has a significant impact on Bell's inequality."
"When the system starts with the product state, both of the quantum dots stay in the ground state, the violation of Bell’s inequality in Case I and III becomes weaker with the rise of the temperature and after the temperature is high enough, it fades out, while in Case II the violation of Bell’s inequality has never been found in the whole time evolution."

XenRE
00.00.0000 00:00Чтоб доказать возможность эмуляции явлений КТ через скрытые переменные — нужно составить 3 последовательности битов так, чтоб при попарном сравнении любых 2 из них в них совпадали ровно 25% значений. Легко доказать, что это невозможно (попробуйте составить сами).

michael_v89
00.00.0000 00:00Нет, достаточно предложить модель, в которой набор скрытых параметров дает тот же результат. В эксперименте Белла 3 последовательности битов не произвольны, это проекции измерения спина/поляризации. Там есть такой эффект, если мы будем выравнивать поляризацию перед измерением с помощью строго вертикального поляризатора, а после него поставим измеряющий прибор под углом, то иногда мы будем получать результат "поляризация горизонтальная", и "иногда" зависит от величины угла.
http://www.eslitak.com/index/0-4
Прибор П1 у нас жестко зафиксирован и работает в качестве источника упорядоченных протонов. Так что в П2 попадают только такие протоны, которые гарантированно пройдут через ПШГ с вертикальной ориентацией. Ну а П2 может поворачиваться вокруг оси, показанной на рисунке штрихпунктирной линией на любой угол α. Теперь посмотрим, как будут срабатывать детекторы при разных значениях угла α.
Для угла в 0° срабатывать будет только плюс-детектор D2+ (это мы уже видели в предыдущем эксперименте, рисунок 1.6). Теперь повернём измеритель на 1° и произведём серию "выстрелов". Здесь мы увидим, что иногда, очень редко, срабатывает минус-детектор D2–.Вот финальный вариант программы, которая моделирует этот эффект, можете запустить в браузере и убедиться, что она дает 1/2, при этом случайные параметры задаются только при инициализации фотонов. Неравенства Белла рассматривают только случайность спина, между фотонами спин (поляризация) коррелирует, а у меня рассматривается дополнительный параметр, который случаен для разных фотонов. Случайное значение при инициализации моделирует в том числе и случайные окружающие факторы в момент подлета фотона к прибору, от которых может зависеть его отражение или прохождение.
Скрытый текст(function() { let basisA = toRadians(0), basisB = toRadians(60), basisC = toRadians(120); let allBasises = [basisA, basisB, basisC]; let resultPass = 1, resultReflect = 0; let distanceToDevices = 100; run(); return; function run() { let matchCount = 0, notMatchCount = 0, totalCount = 1000; for (let i = 0; i < totalCount; i++) { let [photon1, photon2] = create2EntangledPhotons(); let [resultAlice, resultBob] = oneRun(photon1, photon2); if (resultAlice === resultBob) { matchCount++; } else { notMatchCount++; } } console.log(matchCount, notMatchCount, totalCount); } function rand(max) { return Math.random() * max; } function toRadians(degree) { return Math.PI * degree / 180; } function create2EntangledPhotons() { let polarizationDegree = rand(toRadians(180)); let hiddenParameterPhoton1 = rand(toRadians(360)); let hiddenParameterPhoton2 = rand(toRadians(360)); let photon1 = { polarizationDegree: polarizationDegree, initialPhase: hiddenParameterPhoton1 }; let photon2 = { polarizationDegree: polarizationDegree, initialPhase: hiddenParameterPhoton2 }; return [photon1, photon2]; } function oneRun(photon1, photon2) { let basisAlice = allBasises[parseInt(rand(3))]; let basisBob = allBasises[parseInt(rand(3))]; let resultAlice = calcResult(photon1, basisAlice); let resultBob = calcResult(photon2, basisBob); return [resultAlice, resultBob]; } function calcResult(photon, basis) { // phase and amplitude are for E vector let polarizationDiff = Math.abs(photon.polarizationDegree - basis); let maxAllowedAmp = Math.abs(Math.cos(polarizationDiff)); let waveLength = 1; let periods = (distanceToDevices / waveLength); let finalPhase = photon.initialPhase + periods * (2 * Math.PI); let currentAmp = Math.abs(Math.sin(finalPhase)); let shouldPass = currentAmp < maxAllowedAmp; let result; if (shouldPass) { result = resultPass; } else { result = resultReflect; } return result; } })()

XenRE
00.00.0000 00:00У вас ошибки в скрипте: во первых шаг между базисами 120 а не 60, а во вторых статистику надо считать отдельно для совпадающих базисов и отличающихся, и желательно все комбинации отдельно.
Нужно получить 100% совпадение для одинаковых базисов и 25% совпадений для любых отличающихся.
Кстати в статье похоже тоже ошибка, вместо:Получается следующее: если Алиса выберет базис А, Боб – базис B, то вероятность получить 0 в качестве измерения равна 1/4; то же справедливо и для A,C.
Должно быть:
Получается следующее: если Алиса выберет базис А, Боб – базис B, то вероятность получить одинаковый результат при измерении равна 1/4; то же справедливо и для A,C.

michael_v89
00.00.0000 00:00У вас ошибки в скрипте: во первых шаг между базисами 120 а не 60
Я писал выше, почему так.
"В скрипте углы поделены на 2, так как для поляризации нет разницы 0 или 180, это все равно вертикальная поляризация."
Для поляризации выбор не "вверх/вниз" относительно оси измерительного прибора, а "вдоль/поперек" оси.а во вторых статистику надо считать отдельно для совпадающих базисов и отличающихся
Нет, для неравенства Белла нужно считать только процент совпадений и отличий для 2 случайно выбранных базисов из 3 возможных. В статье описана методика, там одна таблица для всех возможных комбинаций. То есть ориентация поляризации фотонов случайная, неизвестная нам, и мы измеряем ее в 2 выбранных базисах. Иногда получаем результат "фотон прошел через прибор, поляризация соответствует измерительной оси", иногда "фотон не прошел (отразился), поляризация не соответствует измерительной оси".

XenRE
00.00.0000 00:00Нет, для неравенства Белла нужно считать только процент совпадений и отличий для 2 случайно выбранных базисов из 3 возможных.
Из статьи:Известно, что в случае одинаковых базисов Алиса и Боб гарантированно получают одинаковый результат.
У вас это не учитывается. А чтоб просто получить 50% совпадений — можно вообще забить на базисы и просто сгенерить рандом с шансом 0.5.

michael_v89
00.00.0000 00:00Действительно, я думал, что у меня тоже будет всегда одинаковый, но там получается 0.66/0.33. Тогда версия с тепловым движением молекул неверна. Скрытый параметр, если он есть, должен быть одинаковый для обоих фотонов, и одинаково влиять на вычисления.
При этом мы знаем, что результаты для различия базисов в 90° всегда противоположны. То есть между ними случайности нет, и можно обойтись одним случайным параметром, результат второго фотона всегда будет противоположен первому. То есть вычисление со скрытым параметром для базиса X должно давать скажем "n", а для базиса X+90° "1 — n". Или для первого "больше 0", а для второго "меньше 0". Своего рода проекция скрытого параметра на угол между базисом и поляризацией фотона. Сходу не получилось придумать подходящий алгоритм, но есть ощущение, что это возможно. Напишу если получится.

XenRE
00.00.0000 00:00Все равно статья получилась из серии «как нарисовать сову». Придумал вот такую математику на замену:
Как и в статье, измерение ведется в 3 базисах, заданных 3 вектороами (A, B, C), с разницей 120гр между ними. В декартовых координатах получаем (sin(a), cos(a)): A(0, 1) B(0.866, -0.5) C(-0.866, -0.5). Результат каждого измерения — один бит.
Скалярное произведение этих векторов будет давать коэффициент корреляции (k = x1*x2 + y1*y2) между измерениями, т.е. если используется один и тот же базис — k = 1 — 100% совпадений, если разные — k = -0.5 — получаем 25% совпадений, как и в статье. По числам все сходится и математика элементарная, но как эти вычисления соотносится с теорией — может кто прокомментировать?


maximw
Нравятся мне статьи про квантовое что-то. Первые несколько абзацев понятны и просты. До первой формулы. И раз, бах, взрыв мозга. Ничего не понимаю, но все еще интересно.
Вспоминается старая картинка "как нарисовать сову".
Это не претензия к автору статьи или перевода. Это, скорее, к себе претензия и общее наблюдение.
braonle Автор
Так давайте разбираться) Лучший способ, конечно, это зачитать книжку оригинала, я сам в неё полез именно потому, что "не понимаю, но всё ещё интересно".
Кеты (конструкция |↑>) – это вектор. В статье пространство двумерное, то есть и координат будет по две, например, |↑> = (1,0) и |↓> = (0,1). В применении к вещественному миру, первая координата – первое событие, вторая – второе событие.
В квантовой физике состояние системы описывается векторами. Любой такой вектор можно записать в виде комбинации базисных векторов (сродни комплексной записи волны в радиофизике). Координата при векторе – вероятность возникновения соответствующего события, так что сумма квадратов этих коэффициентов равна 1.
Допустим, есть два вектора:
A = a1 * |↑> + a2 * |↓> – первый кубит
B = b1 * |↑> + b2 * |↓> – второй кубит
Общее состояние двух векторов можно описать как AB = (a1 * b1 * |↑> * |↑>) + (a1 * b2 * |↑> * |↓>) + (a2 * b1 * |↓> * |↑>) + (a2 * b2 * |↓> * |↓>). Тут же можно заменить переменные: AB = p * |↑> * |↑> + q * |↑> * |↓> + s * |↓> * |↑> + t * |↓> * |↓>. Если pt = qs, то AB можно разложить на произведение двух векторов – тогда они независимы. Если же pt != qs, то разложить AB нельзя, векторы связаны, что и называется "запутаны".
maximw
Большое спасибо за разъяснение. a1, a2, b1, b2 - это скаляры?
braonle Автор
Да, именно так. Всегда пожалуйста)
checkpoint
Только хотел написать такой же коментарий, но меня опередили. :) Все эти обьясняльщики квантового мира только путают людям мозги - они не могут обьяснить без формул, и первая же формула вводит слушателя в ступор.
Обьясните пожалуйста, какое отношение "координата" имеет к "событию". На каком основании связываются несвязываемые сущности ? Прошу обьяснить всё то же самое, но без закорючек, т.е. на словах. Спасибо.
braonle Автор
Скажите, а вы книгу-то посмотрели, перед тем как называть кого-то "объясняльщиком"? А то непонятно Вам, а виноваты почему-то другие.
По сути вопроса есть такой опыт Штерна-Герлаха: электрон улетел наверх – событие раз, улетел наверх – событие два. Можно всё объяснить на пальцах, включая и решение уравнений, только вот это долго и неудобно, поэтому и появляются векторы с матрицами, которые позволяют много строк свернуть в пару символов.
checkpoint
Книгу пока не смотрел, но я хочу понять смогу я её понять или нет (интерес к этой теме есть). Но судя по всему - понять книгу я не смогу, так как не владею соответствующим математическим аппаратом.
braonle Автор
Если не знакомы с векторами и умножением матриц – понять сможете, просто придётся либо на бумажке немного поупражняться, либо верить конкретным значениям на слово. Мне книга понравилась именно тем, что обозначения не вводятся сразу с |x>, а автор начинает объяснение с бинарных значений, постепенно вводя нужный математический аппарат. Курс линала не заменяет, но какой-то жути там тоже нет. Попробуйте, там всё равно первая половина книги написана в стиле Хокинга, хотя именно парадоксы вылезают только с использованием математики.
checkpoint
Ок, спасибо. Меня как раз смутили эти иероглифы Дирака.
И вопрос попутно. Если |↑> = (1,0) и |↓> = (0,1), то что такое (1,1) и (0,0) ? Если эти значения не определены, то это не вектор в классическом представлении.
vassabi
ИМХО это будут "ошибка измерения" (1,1) и "нет сигнала" (0,0) :)
насколько я понял - это все не любые вектора , а точки на единичной сфере (круге для 2мерного случая), поэтому эти точки можно предствить в виде единичных векторов.
А для единичных векторов - сумма квадратов их компонент должна быть всегда равна 1, что не выполняется для (1,1) и (0,0). причем если первый вектор еще можно нормировать и превратить в (\sqrt 2 , \sqrt 2), то с вторым это будет трудновато
acsent1
Для научно популярной статьи, конечно, лучше оставить всем привычное написание векторов (1, 0) и (0, 1). Ну и конечно нужно было начать почему кубит это вектор.
mayorovp
Ну вот, началось...
Вот дальше вы вводите вектора A и B, а также их произведение AB. Что это за произведение? Скалярное, векторное? Какой смысл имеет вектор A+B?
На самом деле это волновые функции, которые можно рассматривать как вектора в фазовом пространстве.
Поскольку у каждого кубита фазовое пространство своё, сумма A+B не имеет смысла, а произведение векторов является тензорным.
kovserg
Тупой вопрос: если тут прямое произведение

AB = p * |↑> * |↑> + q * |↑> * |↓> + s * |↓> * |↑> + t * |↓> * |↓>
т.е.
AB = p*{1,0, 1,0} + q*{ 1,0, 0,1 } + s*{0,1, 1,0}+t*{0,1, 0,1}
тогда почему:
|{1,0, 1,0}+{0,1, 0,1}|^2 = |{1,1,1,1}|^2 = 1^2+1^2+1^2+1^2 = 4
должно быть 1/2 без корней или нет?
braonle Автор
Тут речь про то, что (sqrt(2)/2)*(sqrt(2)/2) ≠ 0*0, что является признаком запутанности кубитов.
Модуль вектора с картинки всё-таки . Как заметили выше, произведение тензорное, то есть (1,0)*(1,0) = (1*1, 1*0, 0*1, 0*0) = (1,0,0,0). Вы же делаете конкатенацию векторов, что некорректно.
. Как заметили выше, произведение тензорное, то есть (1,0)*(1,0) = (1*1, 1*0, 0*1, 0*0) = (1,0,0,0). Вы же делаете конкатенацию векторов, что некорректно.
В целом можно думать о таком произведении, как о состоянии двух частиц. Например, |↑> * |↑> означает, что первая частица в состоянии ↑, и вторая частица в состоянии ↑. Модуль коэффициента при этом произведении равен корню вероятности такого события. То есть в состоянии с картинки две частицы не могут при измерении дать разные результаты, обе будут ↑ или ↓.![]() И да, речь идёт о волновых функциях. Почему так? Потому что предсказания, которые даёт такая модель, подтверждаются экспериментом.
И да, речь идёт о волновых функциях. Почему так? Потому что предсказания, которые даёт такая модель, подтверждаются экспериментом.
kovserg
Не я делаю прямое произведение. В базисе вместо 2х независимых векторов будет 4.