04.04.2023 07:25
naive_bayes 0 1200 Источник

Привет, Хабр! Меня зовут Алан Савушкин (@naive_bayes), я — дата-сайентист в команде Data Science & Big Data «Лаборатории Касперского», и мы отвечаем в том числе за фильтрацию нерелевантных алертов при телеметрии киберугроз в проекте Kaspersky Managed Detection and Response (MDR). 

В данной статье хочу с вами поделиться, как мы решали задачу построения оценки TPR (True Positive Rate) в условиях неполной разметки данных. Может возникнуть вопрос: а что там оценивать? TPR по своей сути всего лишь доля, а построить доверительный интервал на долю легче простого.

\hat{p} - \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}t_{1-\frac{\alpha}{2}} < \theta < \hat{p} + \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}t_{1-\frac{\alpha}{2}}

Спорить не буду, но добавлю, что из статьи вы узнаете:

  • Что даже в использовании такого интервала есть свои условия.

  • Как на основе серии проверки гипотез получить доверительный интервал, используя под капотом гипергеометрическое распределение. А можно ли использовать биномиальное? Спойлер: можно, но тогда важно понимать, на какой вопрос вы отвечаете, пользуясь такой оценкой. Здесь мы рассмотрим задачу с частотной точки зрения.

  • Что будет, если скрестить биномиальное распределение с бета-распределением, и как этот гибрид используется в качестве сопряженного априорного распределения для гипергеометрического распределения. А здесь мы рассмотрим задачу с байесовской точки зрения.

  • И, собственно, в чем прикол этой неполной разметки данных, и как мы докатились до всего перечисленного выше.

Тизер получился обширным, и если вам стало интересно — что ж, тогда давайте разбираться.

Постановка задачи

Начнем с краткого описания, откуда берется неполная разметка данных и почему это проблема.

Итак, наш Kaspersky MDR (Managed Detection and Response) предназначен для защиты клиентской инфраструктуры от киберугроз, и общая схема его работы выглядит следующим образом:

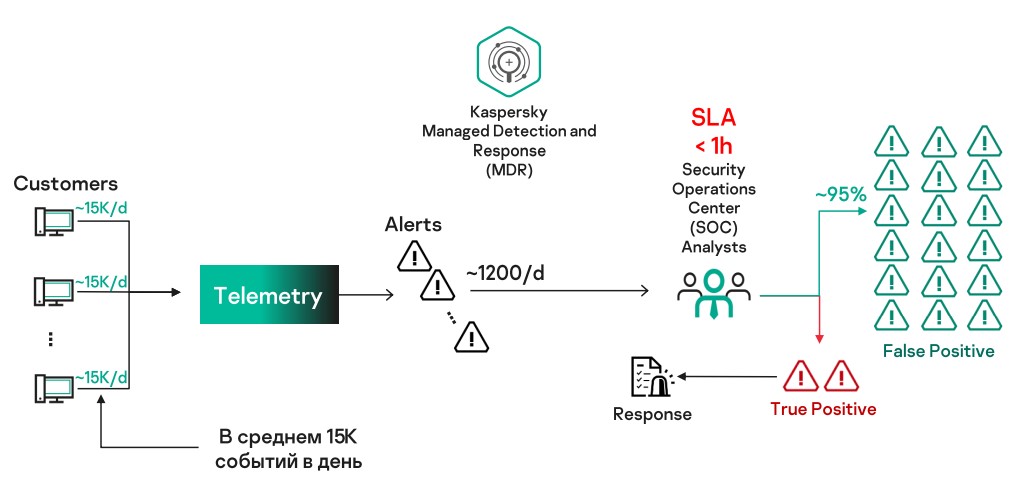
С клиентских хостов передается телеметрия — события, связанные с активностью пользователей. В среднем с одного хоста может поступать около 15 тысяч событий в день. Множество этих событий агрегируется и фильтруется — выделяются подозрительные действия и формируются алерты для отправки аналитикам в Security Operations Center (подробнее о том, как у нас работает SOC, можно прочитать в этой хабрастатье моего коллеги Александра Родченко). В среднем со всех клиентских хостов мы получаем около 1200 алертов в сутки.

Аналитики центра должны расследовать каждый алерт и в случае обнаружения угроз предупреждать клиентов, формируя рекомендации по устранению опасности. Число алертов кажется небольшим, но наши специалисты ограничены во времени — по условиям SLA у них есть не более часа на реакцию.

Как это часто бывает, если нельзя пропустить подозрительное событие, ты слишком бдителен. В итоге большая часть алертов является нерелевантной. Это связано еще и с тем, что для одного клиента определенная активность может быть вполне характерной, а для другого — подозрительной. И здесь мы приходим на помощь аналитикам, вооружившись ML. Задача нашего ML-сервиса — фильтровать нерелевантные алерты, т. е. по факту мы делаем классификатор, который принимает решение, отдать алерт аналитикам или нет. 

Благодаря нашему сервису аналитики меньше времени тратят на нерелевантные алерты, а больше внимания уделяют реальным угрозам. Получается оптимизация ресурсов на обеспечение клиентской защиты — без сервиса «Лаборатории Касперского» пришлось бы расширять штат аналитиков.

Требования и метрики

Нам поставили цель фильтровать 50% потока алертов. За этой метрикой легко следить, поскольку мы знаем, сколько отфильтровываем, а сколько передаем аналитикам. 

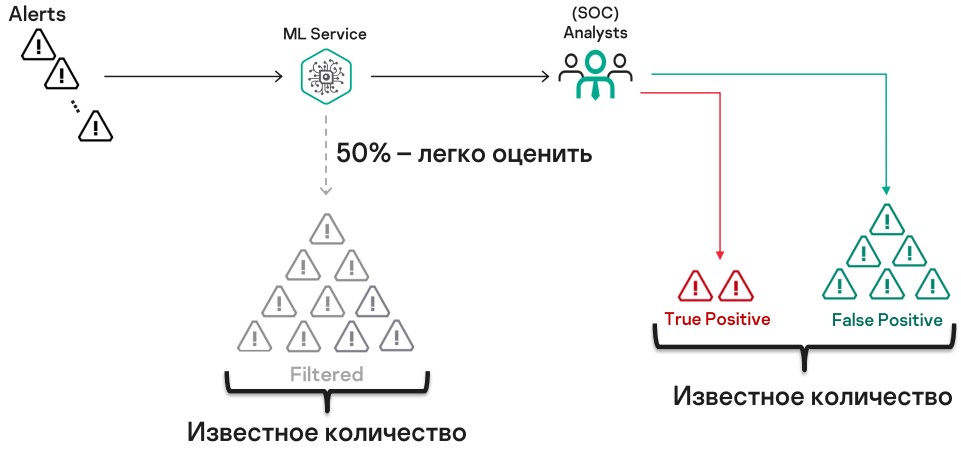
Однако стоит учитывать, что ML-модели неидеальны и возможны ошибки. В нашем случае критичной ошибкой является ошибка 2-го рода (False Negative), то есть что мы отфильтруем релевантный алерт. И в этом плане требование к нашему сервису достаточно высокое — не более 2% пропусков. За этим показателем необходимо тщательно следить в режиме реального времени, чтобы оперативно отреагировать, если что-то пойдет не так. 

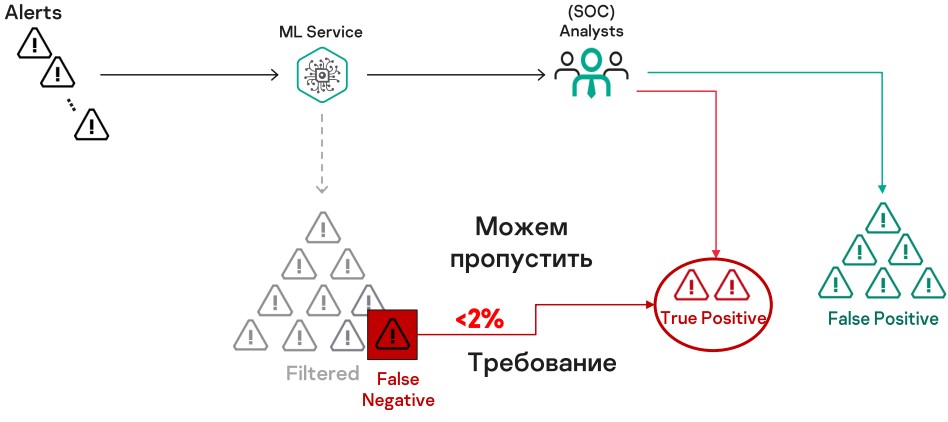
Мы используем метрику True Positive Rate — она должна быть не менее 98%. Напомню, как она считается: 

Здесь:

  • True positive — то, что мы отдали аналитикам, и это действительно оказались релевантные алерты. С этим показателем проблем нет — аналитики посмотрят и все разметят.

  • False negative — то, что неверно отфильтровали. И как получить эту величину, с ходу неясно, потому что как только сервис освободил аналитиков от работы, мы потеряли разметку данных.

Простая перепроверка

Давайте будем брать из потока случайные алерты и передавать их аналитикам для перепроверки, как будто мы ничего не фильтровали. Аналитики отработают в обычном режиме, не зная, что это перепроверка. Но для себя мы отметим, верно ли отработал фильтр. Таким образом, мы получаем разметку данных. 

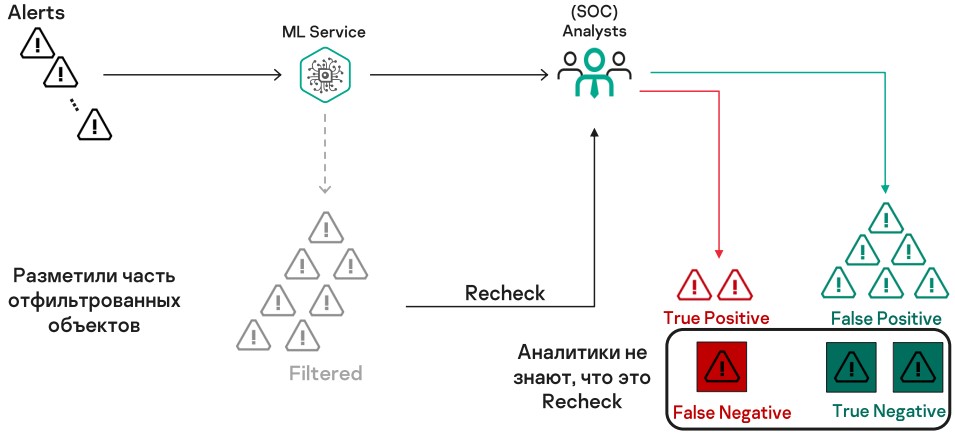
Чтобы понять, достаточно ли информации для использования формулы расчета TPR, проведем симуляцию на синтетических данных и оценим, что можем получить в зависимости от количества переданных на проверку алертов. 

Допустим, мы не перепроверяем ничего — верим нашему сервису. В этом случае формула расчета TPR даст 1.

Ого, это же очень круто! Но голос внутри нас подсказывает, что что-то здесь не так. 

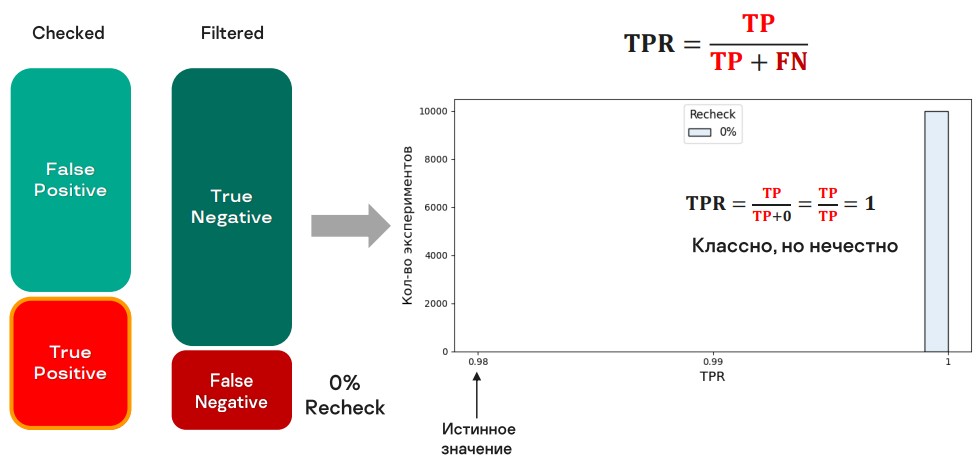
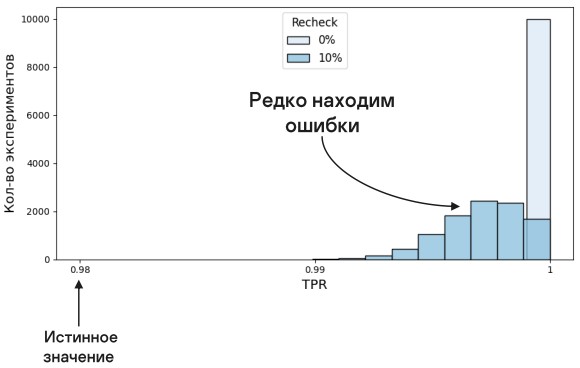
Может, хотя бы что-то отдадим на перепроверку? Если мы передаем на проверку небольшую долю (10%), ошибки обнаруживаются, но редко. Мы все равно слишком позитивны.

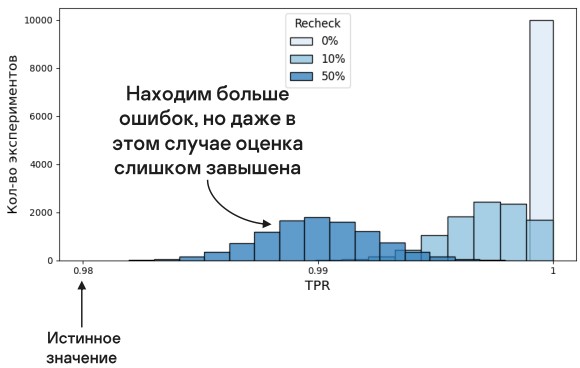
Передавая на проверку 50%, мы можем найти мало или много. Но в среднем это все равно слишком оптимистичный прогноз.

 Только передавая на перепроверку все, мы доходим до истинного значения. 

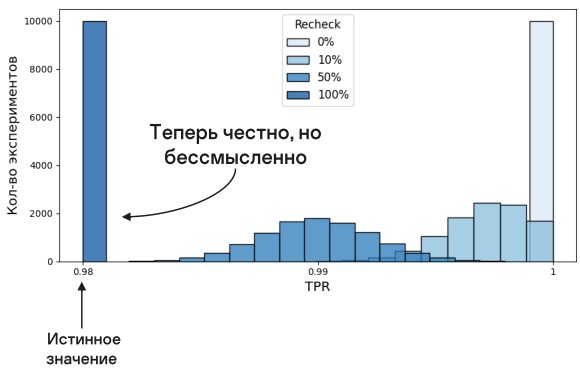
В итоге наивный подход дает нам завышенную оценку. Но нам критически важно следить за реальным качеством сервиса, чтобы оперативно реагировать на изменения картины. Необходимо получить честную оценку, но сохранить пользу от сервиса.

Может возникнуть мысль, что вроде же и так очевидно, что таким способом мы будем получать завышенную оценку. Зачем эти картинки? Согласен, но иногда бывает полезно посмотреть и на очевидные вещи, чтобы стало еще очевиднее=)). Например, здесь мы увидели странную на первый взгляд вещь. Во-первых, сначала у нас разброс такой же, как и когда мы получаем все данные. А во-вторых, когда отдаем 50% на перепроверку, у нас разброс больше, чем когда отдаем 10%, что противоречит предположению, что чем больше данных, тем меньше неопределенность. Но на самом деле здесь нет ничего странного, если понять, какую вероятностную модель использовать. Как раз дальше мы это и рассмотрим. А сейчас отметим самое главное, для чего мы это все описывали.

Вся неопределенность метрики заключается в количестве объектов False Negative, но они находятся в фильтруемой части. То есть точное количество мы не знаем, поэтому нужно каким-то образом оценить границы этой величины за счет нашей схемы перепроверки. То есть здесь мы отвечаем на вопрос: сколько алертов или какую долю алертов мы неверно отфильтровали? Я специально подсветил последнее слово в вопросе — дополнительно мы увидим, что можно отвечать и немного на другой вопрос.

Давайте посмотрим, как эту задачу можно решить с помощью частотного подхода.

Частотный подход

В частотном подходе для оценки границ или выражения неопределенности мы строим доверительные интервалы. Давайте рассмотрим, что это, какие есть способы их построения и какой из способов подходит для нашей задачи.

Доверительный интервал 100(1 – α)%

Доверительный интервал — это интервал, построенный с помощью случайной выборки из распределения с неизвестным параметром, такой, что он содержит данный параметр c вероятностью не менее (1 – α).

Здесь важно понимать, что в частотном подходе у нас выборка случайна и границы являются случайными величинами. А сам параметр является фиксированным, просто мы его не знаем. А вот в байесовском подходе все наоборот, но об этом позже.

Рассмотрим различные способы построения доверительных интервалов и разберемся, какой из способов нам подходит.

Начнем с точного доверительного интервала.

Чтобы получить точный доверительный интервал, необходимо взять статистикуT(\{X_1, \dots, X_n\}, \theta), зависящую от данных и параметра, который хотим оценить. Нам нужна такая статистика, чтобы ее распределение\phiне зависело от параметра \theta. Это позволяет решить уравнение и получить границы. 

P(\phi_l < T(\{X_1,\dots, X_n\}, θ) < \phi_u ) ≥ 1 – α

Предположим, у нас выборка из нормального распределения. Оцениваем среднее — это и будет точный доверительный интервал. 

Пояснение

Пусть наша выборка \{X_1, \dots, X_n\}— независимо и одинаково распределенные (i.i.d.) случайные величины с распределением\mathcal{N}(\theta, \sigma^2).

Здесь у нас E[X] = \theta—мат. ожидание, а D[X] = \sigma^2— дисперсия.

Тогда(X_1 + \dots + X_n) \sim \mathcal{N} (n\theta, n\sigma^2) — тут мы воспользовались тем, что

E[(X_1 + \dots + X_n)] = E[X_1] + \dots + E[X_n] = nE[X]D[(X_1 + \dots + X_n)] = D[X_1] + \dots + D[X_n] = nD[X]

для независимо и одинаково распределенных случайных величин. Тогда получаем

\hat{X}= \frac{1}{n} \sum^n_{i=1} X_i \sim N (\frac{n\theta}{n}, \frac{n\sigma^2}{n^2}) \sim N(\theta, \frac{\sigma^2}{n})\hat{X} - \theta \sim N(0, \frac{\sigma^2}{n}) \Rightarrow \frac{\hat{X}-\theta}{\sigma/\sqrt{n}} \sim N(0,1)

Здесь мы показали, что в случае выборки из нормального распределения статистика T(\{X_1, \dots, \hat{X}_n\}, \theta) = \frac{\hat{X}-\theta}{\sigma /\sqrt n } имеет стандартное нормальное распределение.

И дальше, подставляя нашу статистику в уравнение, получаем:

P\left(\phi_l < \frac{\hat{X}-\theta}{\sigma /\sqrt n } < \phi_u \right) \ge 1 - \alphaP\left(\phi_{\frac{a}{2}} < \frac{\hat{X}-\theta}{\sigma /\sqrt n } < \phi_{1-\frac{\alpha}{2}}\right) \ge 1 - \alpha

где \phi_{\frac{\alpha}{2}},\phi_{1-\frac{\alpha}{2}} — соответствующие квантили стандартного нормального распределения.

P\left(\hat{X} - \frac{\sigma}{\sqrt{n}}\phi_{\frac{a}{2}} > \theta > \hat{X} - \frac{\sigma}{\sqrt{n}}\phi_{1-\frac{a}{2}}\right) \ge 1 - \alphaP\left(\hat{X} - \frac{\sigma}{\sqrt{n}}\phi_{1-\frac{a}{2}} < \theta < \hat{X} - \frac{\sigma}{\sqrt{n}}\phi_{\frac{a}{2}}\right) \ge 1 - \alpha

И в силу симметрии стандартного нормального распределения относительно нуля мы имеем \phi_{\frac{\alpha}{2}}=-\phi_{1-\frac{\alpha}{2}} что в итоге нам окончательно дает привычный вид доверительного интервала

P\left(\hat{X} - \frac{\sigma}{\sqrt{n}}\phi_{1-\frac{a}{2}} < \theta < \hat{X} + \frac{\sigma}{\sqrt{n}}\phi_{1-\frac{a}{2}}\right) \ge 1 - \alpha

Но избавиться от зависимости от параметра при построении интервала получается не всегда. В таких ситуациях используется асимптотический доверительный интервал. Схема его вычисления похожа, просто мы берем «удобное» распределение, чтобы спокойно выводить границы.

Пример.

Допустим, нам надо оценить долю по выборке. Тогда в этом случае мы делаем предположение, что наша выборка \{X_1, \dots, X_n\}— независимо и одинаково распределенные (i.i.d.) случайные величины с распределением Bernoulli(\theta)

Будем действовать, как в примере с точным доверительным интервалом (X_1 + \dots + X_n) \sim Bin (n, \theta) — биномиальное распределение.

Напомню, что у биномиального распределения

E[X] = n\theta, \ D[X] = n\theta(1-\theta)

Тогда распределение выборочного среднего

\hat{X} = \frac{1}{n} (X_1 + \dots + X_n)

это какое-то дискретное распределение с параметрами

E[X] = \theta, \ D[X] = \frac{\theta(1-\theta)}{n}

Такое распределение не имеет определенного названия. Идем дальше.

Статистика \hat{X}-\theta— это какое-то дискретное распределение с параметрами

E[X] = 0, \ D[X] = \frac{\theta(1-\theta)}{n}

И наконец, статистика

\frac{\hat{X}-\theta}{\sqrt{\theta(1-\theta)/\sqrt{n}}}= \sqrt{n}\frac{\hat{X}-\theta}{\sqrt{\theta(1-\theta)}}

это какое-то дискретное распределение с парметрами

E[X] = 0, \ D[X] = 1

Итак, мы получили какое-то дискретное распределение, мы знаем его некоторые характеристики, но им неудобно пользоваться, так как мы не знаем его явного вида и непонятно, как получить нужные нам квантили.

И здесь нам на помощь приходит центральная предельная теорема (ЦПТ), в которой утверждается, что

\sqrt{n}\frac{\hat{X}-E[x]}{\sqrt{D[X]}} \to N(0,1)

по распределению при n \to \infty. А вот это уже удобно, так как из этого распределения мы можем легко получить нужные нам квантили. Но пока мы решили лишь половину проблемы. Давайте подставим полученную статистику в уравнение, которое нам надо решить. Сделаем это уже с учетом ЦПТ.

P\left(\hat{X} - \sqrt{\frac{\theta(1-\theta)}{n}}\phi_{1-\frac{\alpha}{2}} < \theta < \hat{X} + \sqrt{\frac{\theta(1-\theta)}{n}}\phi_{1-\frac{\alpha}{2}}\right) \ge 1 - \alpha

Однако здесь получается замкнутый круг. Чтобы оценить границы неизвестного параметра, нам нужно знать этот неизвестный параметр=)). Чтобы из него выйти, воспользуемся законом больших чисел (ЗБЧ): \hat{X} \to E[X], n \rightarrow∞Тогда в левой и правой части неравенства заменим \thetaнашей оценкой \hat{X}. В итоге получаем

P\left(\hat{X} - \sqrt{\frac{\hat{X}(1-\hat{X})}{n}}\phi_{1-\frac{\alpha}{2}} < \theta < \hat{X} + \sqrt{\frac{\hat{X}(1-\hat{X})}{n}}\phi_{1-\frac{\alpha}{2}}\right) \ge 1 - \alpha

Такой вид интервала для доли, думаю, знаком многим из вас. Его легко построить, но чтобы к нему прийти, нам по пути пришлось сделать несколько допущений. Первое — это сходимость к стандартному нормальному распределению. Но тут как раз нюанс в сходимости к распределению, так как скорость сходимости для различных значений доли не одинакова.

Рассмотрим на картинках для наглядности.

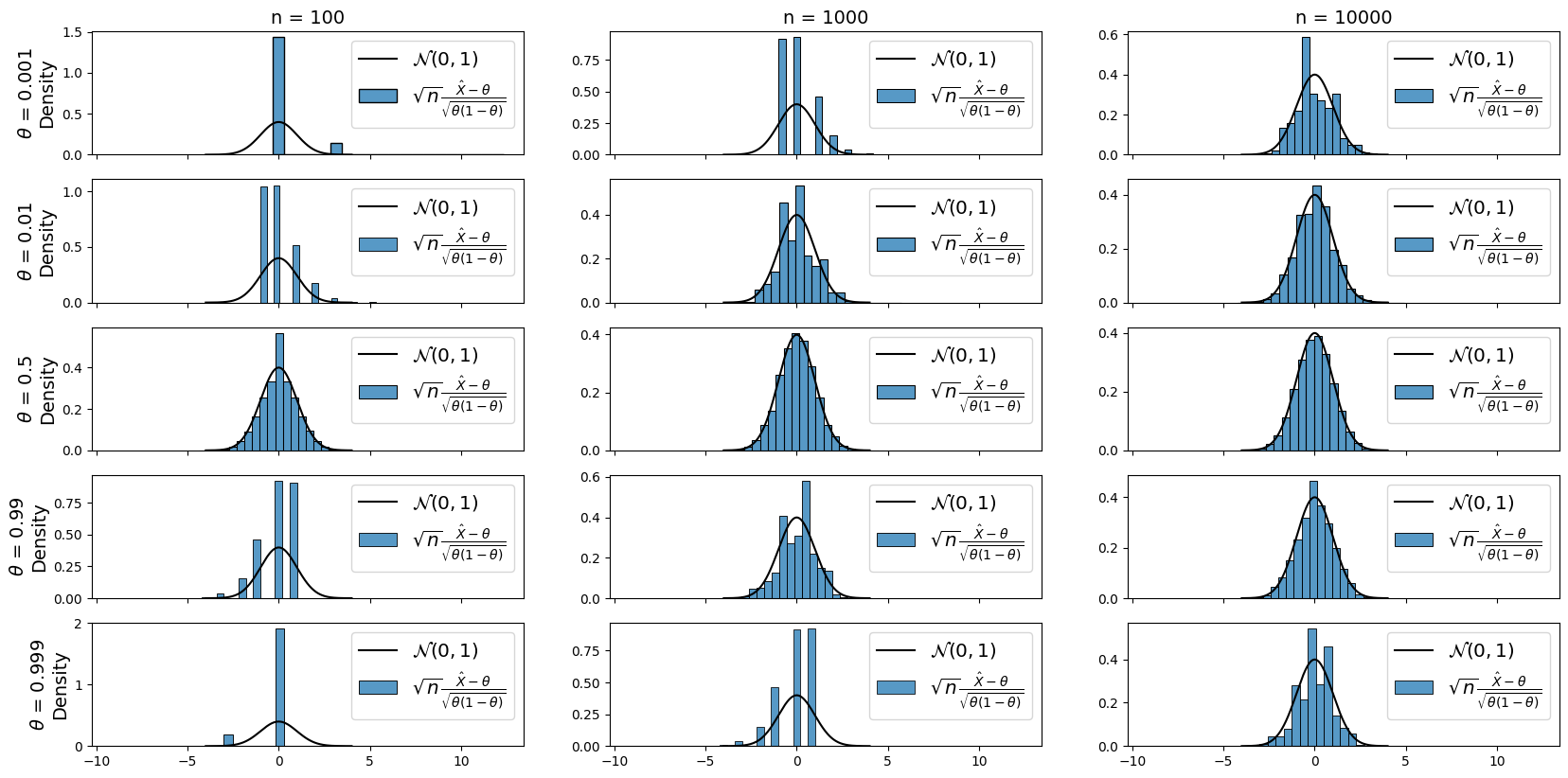
Как видно из графиков, при \theta=0.5распределения статистики к стандартному нормальному распределению наиболее быстрая. А вот для крайних значений \thetaсходимость медленная, и более того — видно, что при аппроксимации нормальным распределением мы не учитываем асимметрию распределения нашей статистики.

Второй нюанс — это замена \theta(1-\theta)на \sqrt{\hat{X}(1-\hat{X})}. Как можно заметить из вида интервала, если мы случайно получим крайние значения для оценки доли, то наш интервал выродится в точку. Причем неважно, много или мало наблюдений нам доступно. И это может приводить к тому, что наш доверительный интервал не будет накрывать истинное значение параметра с нужной нам вероятностью. Рассмотрим графики coverage probability для наглядности.

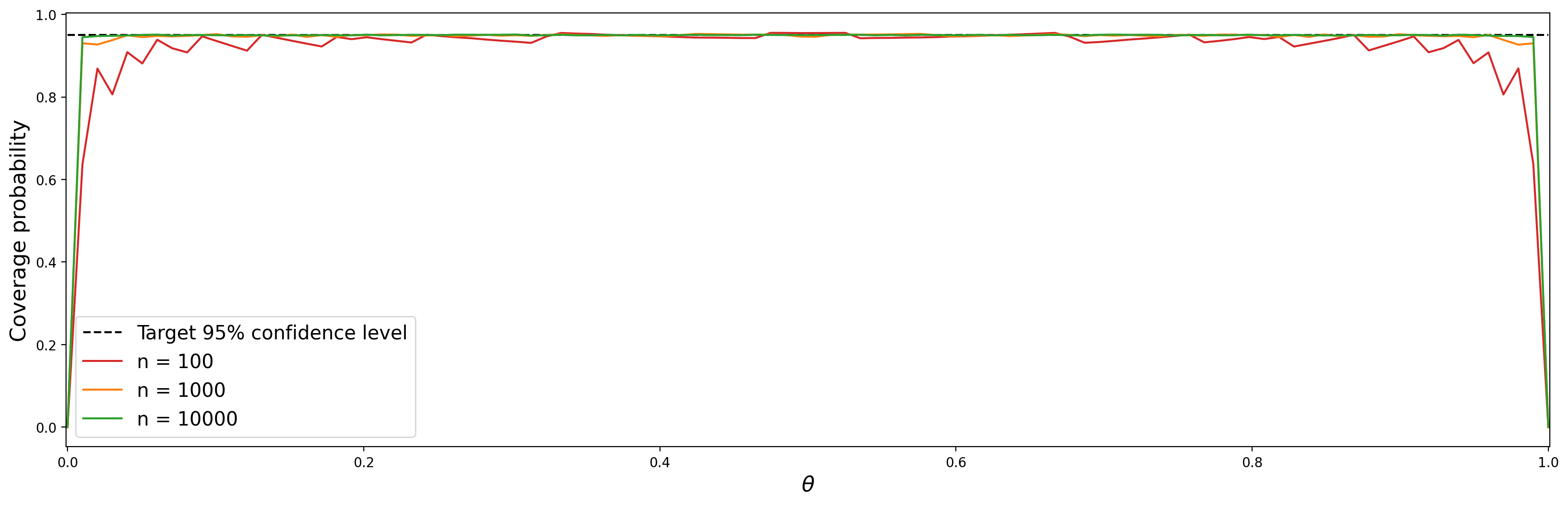
Как видно из графика, если у нас немного данных, то для значений параметра \theta, близких к крайним значениям, наш асимптотический доверительный интервал будет накрывать истинное значение параметра реже, чем мы предполагаем.

Все это в совокупности может приводить к более частым ошибкам первого рода. Так что учитывайте эти нюансы, когда используете какую-нибудь аппроксимацию=) .

Метод еще проще — бутстреп. Мы просто сэмплируем подвыборки и много раз считаем на них распределение. Получаем набор значений, по которым можно вывести границы.

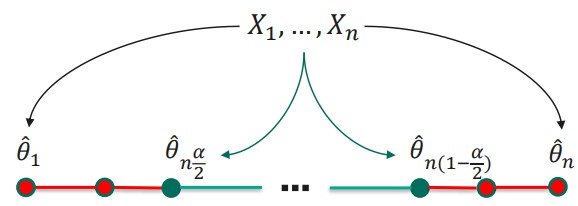
Здесь приведен пример перцентильного доверительного интервала на основе бутстрепа. Об остальных можно прочесть вот тут.

Об еще одном методе говорят редко. Он возникает из интерпретации доверительного интервала и его взаимосвязи с проверкой гипотез.

Доверительный интервал 100(1 – α)% — это область значений параметра θ, для которых мы не отвергаем гипотезу H0: θ = θ0 на уровне значимости α. Иными словами, доверительный интервал — это те значения параметра, которые согласуются с нашими данными при заданном уровне значимости.

Чтобы построить этот интервал, мы фиксируем значение θ и проверяем нулевую гипотезу о равенстве параметра этому фиксированному значению. Значение нам подходит, если мы не можем отклонить нулевую гипотезу. И проверку надо выполнить для всех допустимых значений θ.

Нам нужно собрать все θi, для которых pvalue > α/2 (уровень значимости здесь α/2, поскольку мы ищем две границы).

Тут достаточно простая процедура, самое главное — определиться с вероятностной моделью для проверки гипотезы.

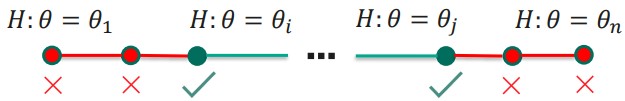
И вы, наверное, уже догадались, что не просто так этот метод упоминается. Да, это действительно так, и давайте разберемся, почему. Для этого рассмотрим более формально нашу систему перепроверки.

Доверительный интервал для выборки без возвращения

Когда мы передаем аналитикам алерты на проверку, они уже не могут считаться отфильтрованными. Таким образом, у нас модель выборки без возвращения.

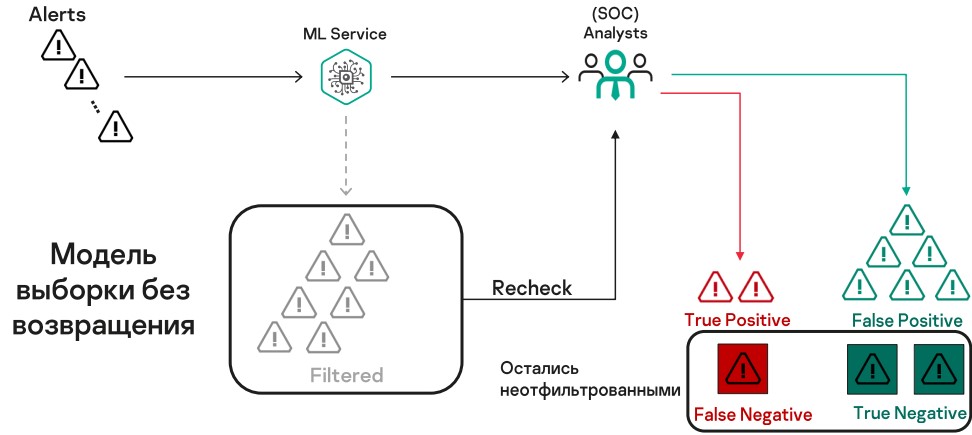
Эту модель стоит рассмотреть более формально. Пусть:

  • N — количество отфильтрованных алертов, мы это знаем;

  • M — сколько всего False Negative отфильтровали, это величину мы не знаем и хотим оценить;

  • n — сколько объектов отдали на перепроверку (и это мы знаем);

  • k — сколько False Negative алертов нашли на перепроверке (это тоже знаем).

Такая модель описывается гипергеометрическим распределением.

Итак, мы знаем величины N, k, n, а величину M нам нужно оценить. И с ходу неясно, какую нам статистику считать по выборке, чтобы воспользоваться первыми тремя способами построения доверительных интервалов.

В теории мы могли бы просто оценивать долю \frac{M}{N} с помощью статистики p=\frac{k}{n}. Строить интервал для доли \frac{k}{n}, потом выводить границы для M, как M \sim (N\times p_{lower}; N\times p_{upper})

Но тут у нас несколько проблем. Первое — мы можем очень редко находить алерты False Negative. Соответственно, у нас k может быть часто нулевым. В таком случае использовать бутстреп и асимптотический метод нецелесообразно, так как в обоих случаях у нас проблемы со сходимостью, и интервалы, по сути, вырождаются в точку, а именно в ноль. Тогда и оценка величины M будет часто нулем, и мы опять слишком позитивны.

Мы могли бы использовать точный интервал, но в этом случае M может оказаться дробным и неясно, в какую сторону его округлять. При больших M такого вопроса не возникает, но при малых мы можем ошибочно сместить оценку, что в итоге скажется на TPR.

Кстати, интересно, что точный интервал для доли, а именно интервал Клоппера —Пирсона — это на самом деле интервал, основанный на четвертом методе построения интервала, просто он красиво сводится от перебора значений к прямому вычислению нужных квантилей. Здесь хорошо об этом написано, плюс мы еще затронем этот интервал в нашей статье.

В итоге только один из обсуждавшихся методов на основе проверки гипотез учитывает все особенности.

Построение доверительного интервала на практике

Рассмотрим на примере, как строить такой интервал.

Предположим, мы отфильтровали 1000 алертов (N = 1000) и хотим оценить параметр M — построить 95%-ный доверительный интервал.

100 алертов отдали аналитикам (n = 100), 25 нашли на перепроверке (k = 25). Все эти величины мы уже можем подставить в гипергеометрическое распределение:

Параметр M неизвестен, но мы можем предположить, что он равен какому-то значению. Так у нас появится фиксированное гипергеометрическое распределение — мы проверяем гипотезу о равенстве параметра этому значению.

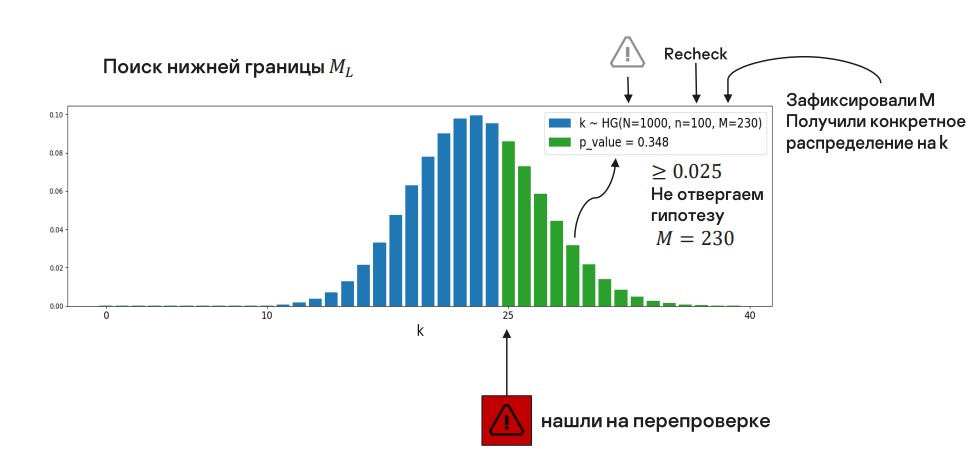
Сначала рассмотрим поиск нижней границы M_LФиксируем величину M и вычисляем pvalue — в данном случае правый хвост распределения от величины k. Интуитивно это похоже на проверку, а не слишком ли много мы достали объектов False Negative в предположении, что всего их M штук в нашей отфильтрованной части.

В первом случае значение P_{value} > \frac{\alpha}{2} = 0.025, нам оно подходит.

Пробуем уменьшить M.

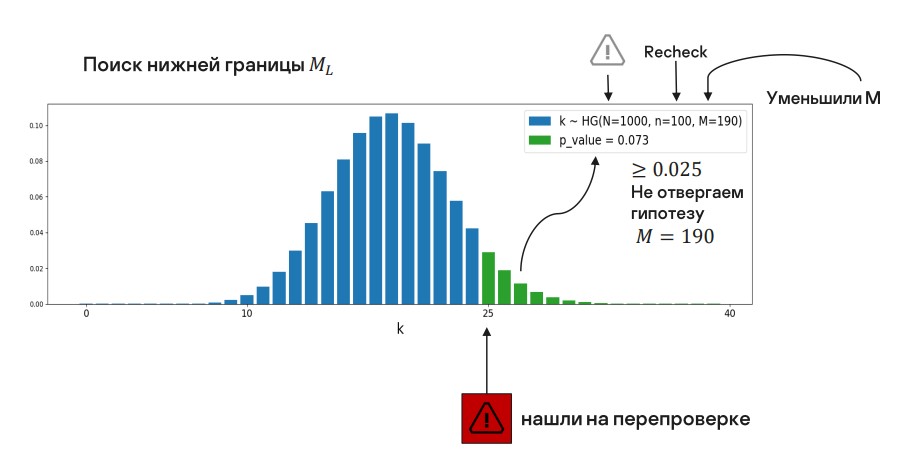
Наше распределение сместилось, вследствие чего pvalue уменьшилось, но это значение нам также пока подходит. Двигаемся дальше.

Следующее значение мы получаем на грани.

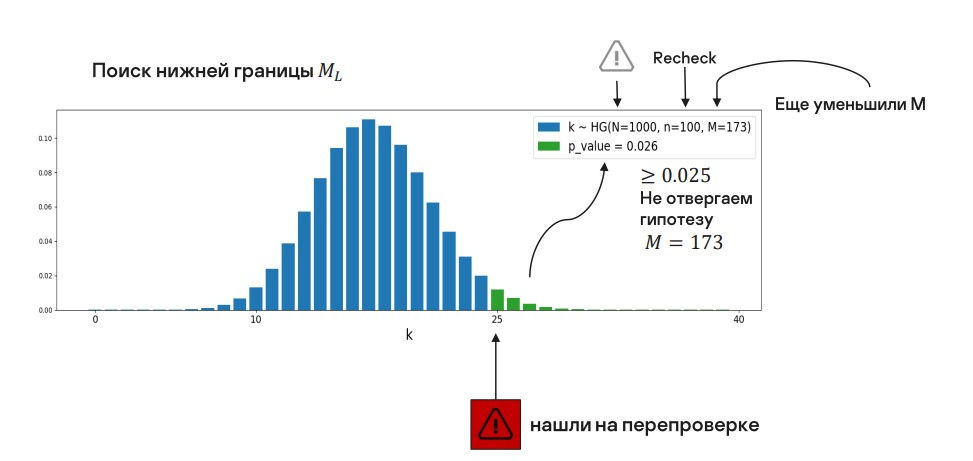
Мы пока не отклоняем нулевую гипотезу, но если сместимся еще на единицу, ее придется отклонить при нашем уровне значимости.

Нам нужно последнее подходящее значение, поэтому мы берем предыдущее.

Аналогично выглядит поиск верхней границы, но все зеркально. M необходимо увеличивать и проверять для конкретного числа. Pvalue — это теперь левый хвост распределения. Здесь интуиция такая: а не слишком ли мы мало достали объектов False Negative в предположении, что всего их M штук в нашей отфильтрованной части.

Будем двигаться все выше и выше, пока не отклоним нулевую гипотезу. И возьмем значение, которое подходило последним.

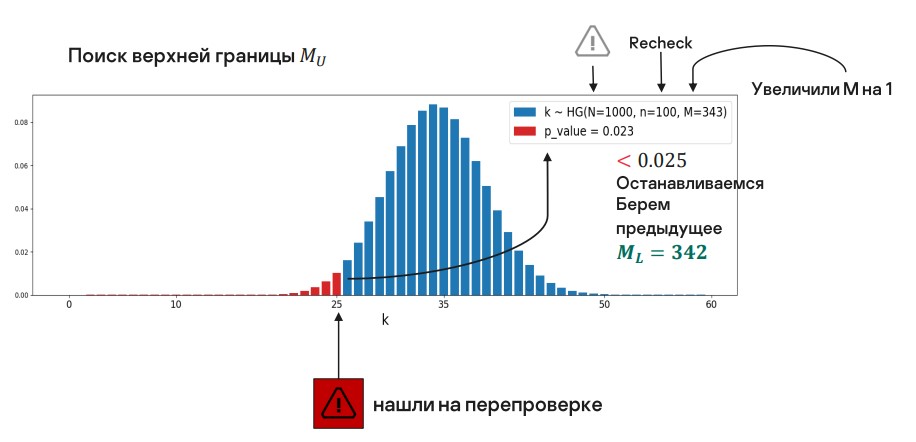
Верхняя и нижняя границы найдены — можно строить интервал для TPR, подставив их в исходную формулу.

Доверительный интервал в динамике

Рассмотрим, как интервал выглядит в динамике.

Предположим, мы запустили сервис. На перепроверку отдаем 15% алертов. Эта величина была выбрана в качестве своеобразного trade-off, чтобы интервалы оставались широкими не так уж долго — чтобы мы быстрее набирали данные, но при этом все же могли отфильтровывать более 50% алертов.

Как видно на графике, сразу после запуска сервиса данных пока мало, а неопределенность высока. Но со временем мы набираем данные, и интервалы сужаются.

Дополнительно на этом графике выведен результат «наивного» подсчета — он показывает, насколько в этом случае мы позитивно к себе относимся. Нам такой вариант не подходит.

Здесь важно отметить, что наши интервалы покрывают целевое значение, т. е. мы не можем отклонить гипотезу о том, что TPR = 0,98 и можно спать спокойно. Этот «универсальный» подход ненамного сложнее стандартных методов, но решает проблему завышенной оценки.

Использование интервала Клоппера — Пирсона

В самом начале и по ходу статьи упоминалось, что можно строить так называемый точный интервал Клоппера — Пирсона на основе биномиального распределения. Давайте разберем, как его можно построить — и как от этого меняется вопрос, на который мы себе отвечаем.

Выше мы видели, что «наивный» подсчет TPR дает нам завышенную оценку. Решение этой проблемы, которое было представлено выше, опиралось на то, что величина TP (True Positive — отдали релевантный алерт) у нас полностью известна и фиксирована, а вся неопределенность у нас в величине FN (False Negative — отфильтровали релевантный алерт). Но «наивный» подсчет можно подправить еще одним способом.

Еще раз посмотрим на наивный подсчет TPR более наглядно.

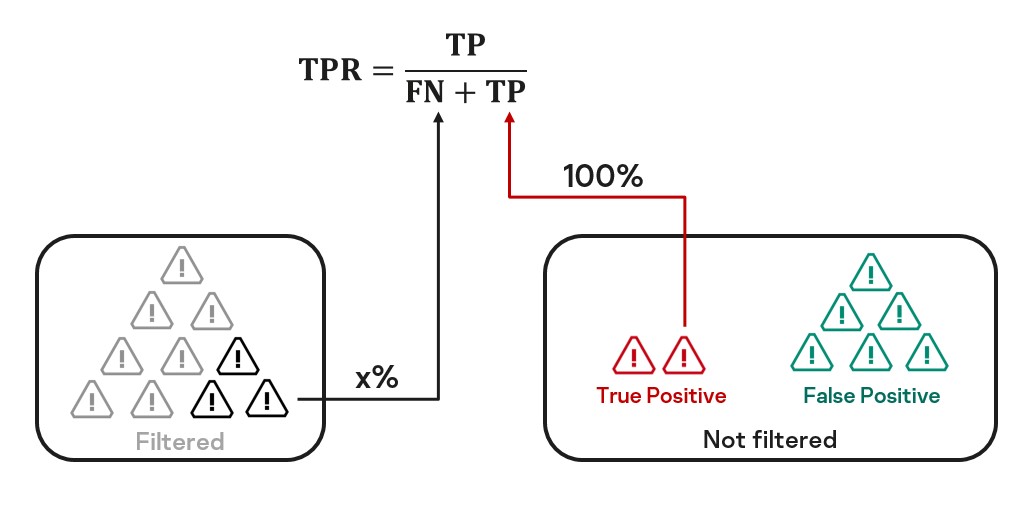
Из картинки видно, что мы в неравной степени учитываем объекты из двух групп (Filtered и Not filtered). То есть наша выборка нерепрезентативна для оценки доли. Чтобы это исправить, нам нужно сделать так, будто мы из группы Not filtered берем тоже x% от алертов True Positive. Это сделать достаточно просто, а именно — в формуле для TPR умножить число TP на \frac{x}{100}, то есть на долю перепроверки. Тогда это будет равноценно тому, что мы в равной степени берем объекты из двух групп.

Давайте теперь проведем симуляцию нашей схемы перепроверки и посмотрим, что мы получим в этом случае.

Ага, видим теперь, что скорректированный TPR дает нам несмещенную оценку. Еще видим, что при увеличении процента перепроверки у нас уменьшается дисперсия оценки. Здесь мы убрали случай, когда мы не проверяем наш сервис, так как с точки зрения математики получаем неопределенность, по формуле получаем \frac{0}{0}. Но важно отметить, что это согласуется с интуицией, так как, ничего не проверяя, мы в полной степени не уверены в том, что там у нас происходит.

Также видим знакомую картину — ее мы уже видели, когда рассматривали асимптотический доверительный интервал для доли. А именно: если давать на перепроверку не много данных, распределение статистики несимметрично, и тогда не совсем корректно использовать асимптотический доверительный интервал на основе нормального распределения.

Здесь нам на помощь приходит интервал Клоппера — Пирсона. По сути, этот интервал строится тем же методом, что мы описали выше. Просто в данном случае мы перебираем сразу значения для доли, то есть значения TPR. А в статистическом тесте теперь мы используем биномиальное распределение. Грубо говоря, проверяем следующее: «Окей, а какова вероятность увидеть такие или еще более экстремальные данные в предположении о том, что доля имеет конкретное значение?», как с фиксированием параметра M в методе выше. Методы аналогичны, просто под капотом используем разные распределения. И если вы разобрались в методе, который мы описали ранее, то с этим методом будет еще проще. Но тут дополнительно приходит на помощь связь биномиального распределения с бета-распределением, и поэтому в данном случае нам не требуется перебирать значения для доли. Границы можем получить сразу, вычислив квантили соответствующего бета-распределения.

Важно отметить, что здесь получаются немного другие обозначения. Теперь параметр \theta который мы хотим оценить, это непосредственно TPR.

Величина

n = FN + \frac{x}{100}TP

— размер выборки.

Величина

k= \frac{x}{100}TP

— количество верно отфильтрованных алертов в нашей выборке.

Тогда

P(k) = \left(\frac{n}{k}\right)\theta^k(1-\theta)^{n-k}

— наше биномиальное распределение.

Здесь может возникнуть вопрос: вроде бы биномиальное распределение — это про схему выборки с возвращением, а тут у нас выборка без возвращения, как же так? Действительно, на практике почти всегда, по сути, мы имеем выборку без возвращения, да и размер генеральной совокупности тоже не бесконечен. Но в нашем случае, когда размер выборки (величина n) много меньше размера генеральной совокупности (величина N), из которой мы сэмплируем, схему выборки без возвращения можно заменить схемой выборки с возвращением. То есть мы аппроксимируем гипергеометрическое распределение биномиальным.

А почему мы можем сделать предположение, что n << N в нашей задаче? Здесь все просто: мы считаем, что наша генеральная совокупность — это алерты, по которым еще не вынесли вердикт аналитики или которые должны быть в будущем. То есть наша оценка теперь предполагает такую схему:

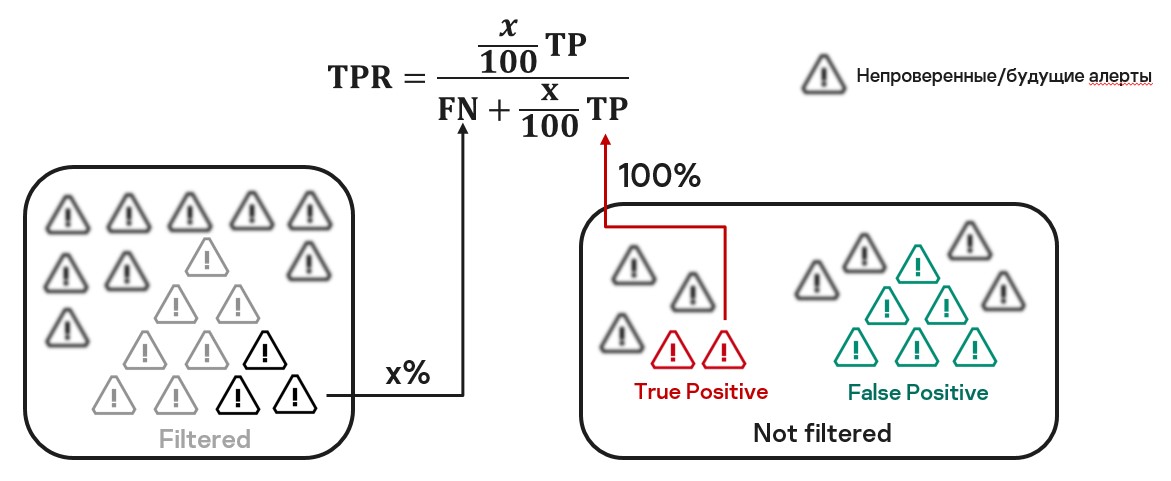
Давайте рассмотрим в динамике доверительные интервалы, построенные с помощью двух методов, и сравним их.

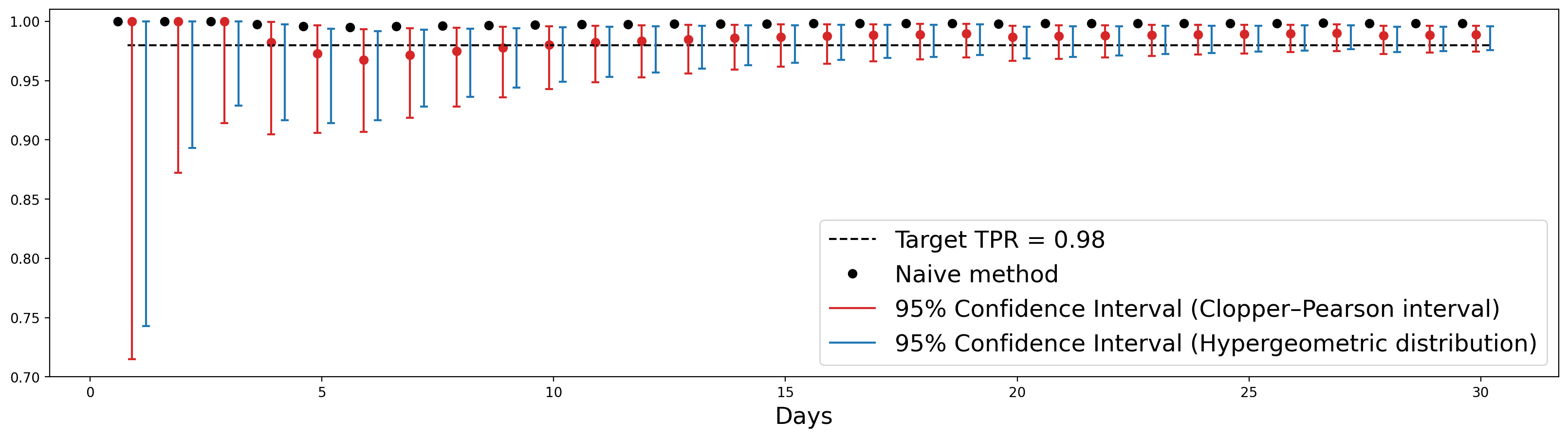
На графике мы дополнительно отметили красными точками скорректированный TPR. Первое, что видим по красным доверительным интервалам, это то, что доверительные интервалы вовсе не обязаны быть симметричными. И это логично, так как за 1 мы выйти не можем, и ранее мы видели, что в крайних значениях для доли распределение статистики у нас не симметрично. Второе: видим, что интервалы Клоппера — Пирсона шире, чем интервалы на основе гипергеометрического распределения, что тоже соответствует тому, что мы моделируем и оцениваем. Если раньше мы отвечали на вопрос, сколько или какую долю алертов мы отфильтровали, то теперь мы отвечаем на вопрос, сколько или какую долю алертов мы фильтруем. То есть мы распространяем нашу неопределенность еще и на будущее.

Байесовский подход

Если вам не по душе частотный подход с его формулировками на тему повторения экспериментов с целью получить в 95% случаев какой-то результат, можно использовать другой подход — байесовский. Как и частотный подход, он используется, чтобы как-то выразить неопределенность в отношении параметра, и в какой-то степени больше выражает нашу житейскую интуицию. Если в частотном подходе параметр — фиксированная величина (хоть и неизвестная), в байесовском мы сразу рассматриваем распределение на искомое значение.

Распределением мы выражаем нашу уверенность в определенных значениях (в одних мы уверены больше, в других меньше, исходя из данных). По-разному мы интерпретируем и доверительный интервал.

В частотном подходе это в большей степени бинарный вывод — подходит или не подходит значение, т. е. это область значений, которые мы не отвергаем на уровне значимости α. В байесовском подходе мы выражаем эмоции, подразумевая, что с вероятностью (1 – α) значение параметра лежит в заданной области. У меня это ассоциируется с фразой «примерно что-то где-то там»=).

Апостериорное распределение

После запуска сервиса мы постепенно собираем данные. Апостериорное распределение — это наша уверенность в значениях параметра уже после того, как некоторые данные получены.

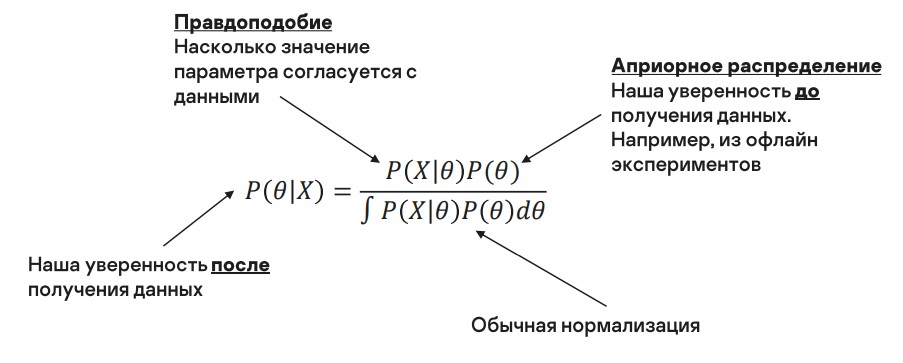
Апостериорное распределение включает следующие элементы:

  • правдоподобие — насколько значения параметра согласуются с нашими данными (это мы уже использовали в предыдущем подходе);

  • априорное распределение — это наше знание до проведения экспериментов и получения данных: например, мы могли получить нашу уверенность в значениях из офлайн-экспериментов и затем использовать ее на проде;

  • обычная нормализация, чтобы все суммировалось в единицу.

К нашей задаче это применимо следующим образом. Символов стало больше, но сейчас я напомню, что они означают:

  • N — известная величина, сколько отфильтровали (в нашей схеме мы знаем эту величину);

  • n — сколько отдали аналитикам на перепроверку;

  • k — сколько пропустили;

  • M — искомый параметр;

  • в знаменателе дроби — все та же нормализация.

Часто в литературе можно увидеть в качестве индексов N и M, а не как у нас — N-n и M-k.

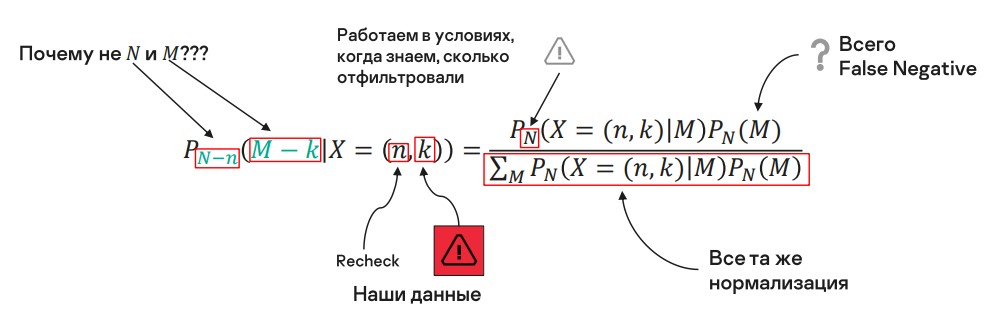
Мне указание только лишь N и M не очень нравится, потому что, судя по форумам, это смущает людей. Важно писать именно N-n и M-k, потому что здесь появляется смещение. Мы рассматриваем схему выбора без возвращения. Когда что-то передаем аналитикам для перепроверки и получаем данные, неопределенность остается только в том, что мы не отдавали — как раз для этого множества алертов мы и выражаем неопределенность.

На данный момент мы имеем следующее. Мы не знаем априорное распределение, но уже можем указать правдоподобие — помним, что у нас схема выборки без возвращения и гипергеометрическое распределение.

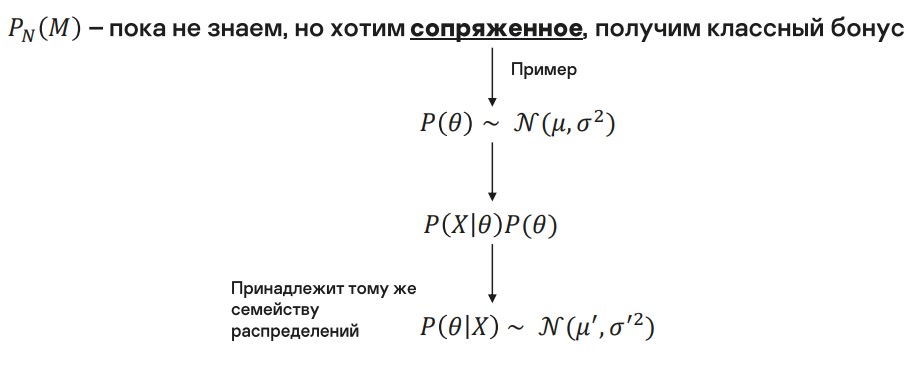
Априорное распределение

Априорное распределение нам неизвестно, но было бы удобно, если бы оно было сопряженным. Например, предположим, что априорное распределение является нормальным. Объединив это с правдоподобием, получим нормальное апостериорное распределение. Это и означает, что априорное распределение — сопряженное.

Имея сопряженное априорное распределение, в качестве бонуса мы получаем удобство расчетов.

Вернемся к схеме фильтрации, чтобы вывести априорное распределение.

С какой-то вероятностью в нашей корзине один алерт будет False Negative (неверно отфильтрованным). Здесь мы можем применить схему Бернулли. Если алерт один — это распределение Бернулли, а когда их много — это биномиальное распределение.

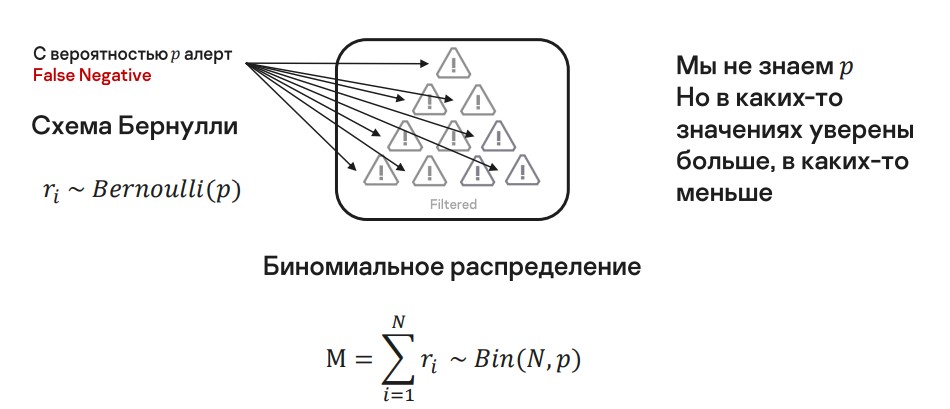
Параметр p нам неизвестен, но мы опять же можем рассмотреть нашу модель при каком-то значении параметра.

Зафиксируем некоторое значение параметра p и тогда получим вполне определенное биномиальное распределение. Я привел несколько на изображении ниже, там же я показал априорное распределение, которое выражено бета-распределением. По ходу дела мы увидим, почему именно его берем.

Но уверенность в разных значениях p разная. Допустим, p = 1. Это значит, что все, что мы отфильтровали — False Negative, но это не так (мы все-таки верим в нашу модель).

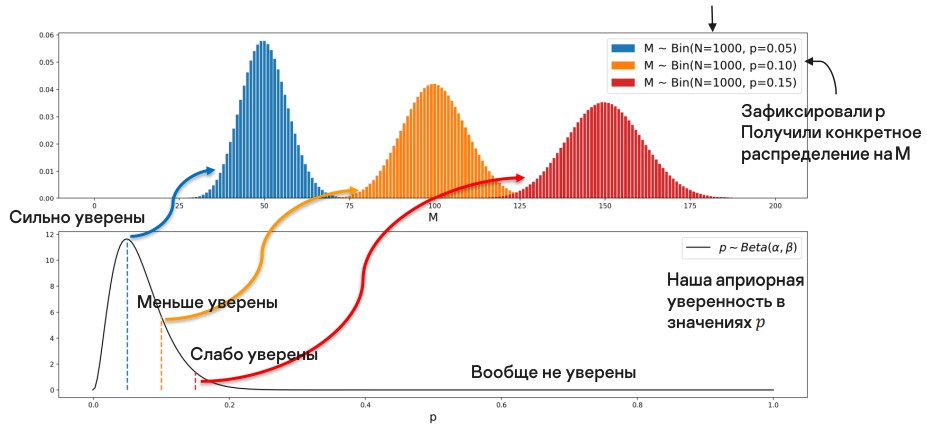
Таким образом, у нас есть несколько биномиальных распределений. Чтобы получить одно распределение, их нужно объединить, причем пропорционально нашей уверенности в каждом из них.

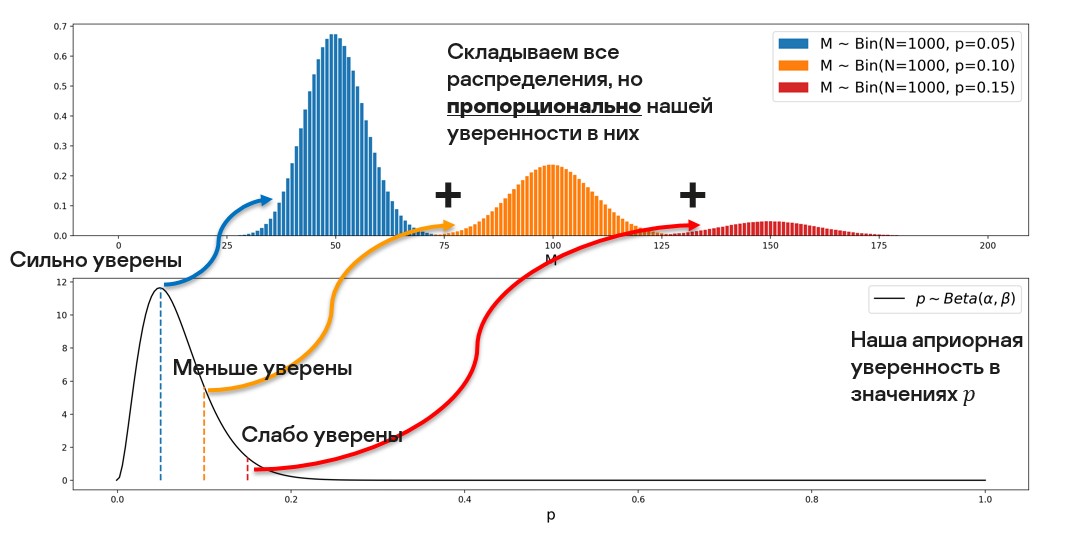
Рассмотрим это более формально. Здесь приведено биномиальное распределение (при фиксированном параметре p). Априорное распределение при этом выражено бета-функцией.

Если вас пугает вид бета-функции, то расслабьтесь, сам интеграл в этой функции нам не важен=). Самое главное для нас — это то, как аргументы бета-функции соотносятся со степенями в выражении этой функции. Просто подставим все известные выражения в интеграл. В результате магии чисел мы получаем также бета-функцию, но уже с другими аргументами, А штука, которую мы получили в результате, называется бета-биномиальным распределением.

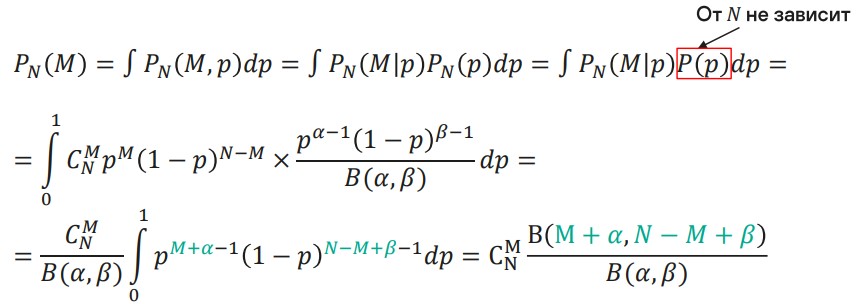
Бета-биномиальное распределение интерпретируется как схема Бернулли с неизвестной вероятностью «успеха». А это как раз то, что мы имеем в нашей схеме перепроверки.

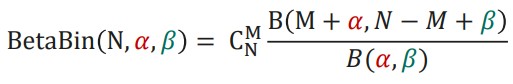
Параметры α и β — это наши априорные знания:

  • α — количество «успехов» до опыта (количество алертов False Negative, полученных, например, в офлайн-экспериментах, когда мы тестировали модель);

  • β — количество «неудач» до опыта (количество алертов True Negative — то, что мы верно отфильтровали).

Здесь может показаться немного странным употребление слов «успех» и «неудача». Это в своем роде устоявшиеся обозначения для схемы Бернулли. Особенно если вспомнить о применении этой схемы в моделировании неисправностей приборов или, более того, в оценке рисков, где успехом считается неблагоприятное с точки зрения жизни событие. Поэтому в данном случае мы использовали эти обозначения в кавычках.

Итак, мы получили апостериорное распределение следующего вида:

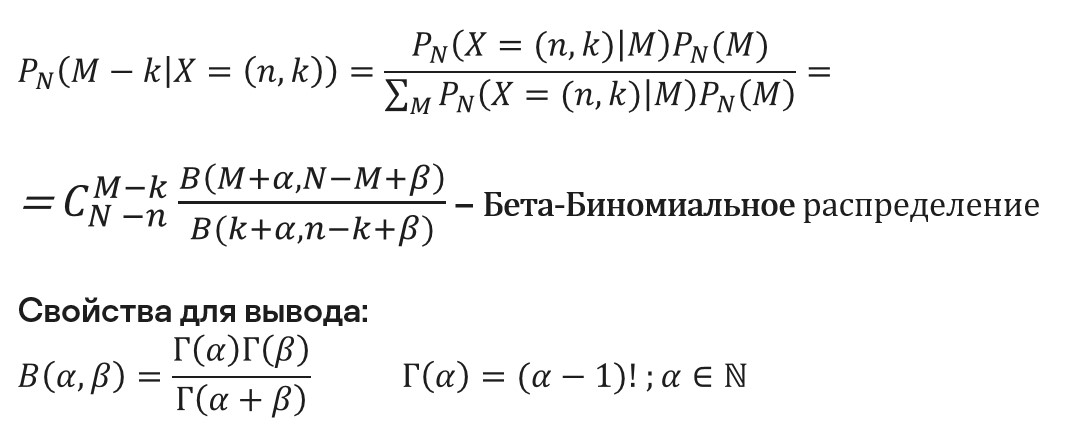
Я привел свойства для вывода — нам необходимо пожонглировать факториалами и сочетаниями. Важно, что в итоговой формуле мы явно видим смещение на параметр M, т. е. схема как раз учитывает, что мы сделали выборку без возвращения.

Итак, мы искали сопряженное априорное распределение. И это дало нам огромный бонус — весь байесовский вывод удалось свести к простому сложению-вычитанию (пересчету параметров).

Байесовский доверительный интервал

Рассмотрим, как это будет выглядеть на примере.

Предположим, изначально мы не уверены ни в каких значениях.

Мы выполнили перепроверку и получили какие-то данные. Далее мы пересчитываем параметры и получаем новое бета-биномиальное распределение (при этом мы не забываем о смещении).

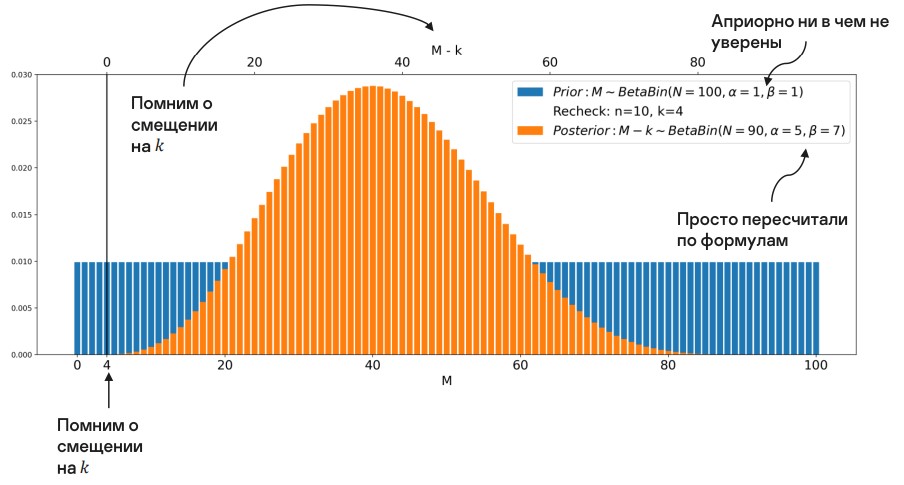
Имея построенное распределение, можем выделить область значений, в которых мы в наибольшей степени уверены. Это и будут границы количества алертов, которые мы неверно отфильтровали.

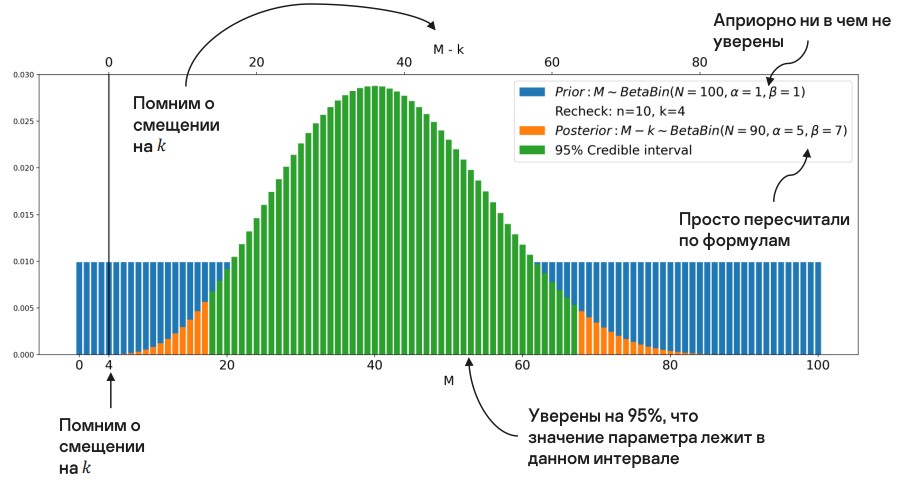
Посчитаем TPR.

Мы построили границы, вспомнили о смещении. Теперь, чтобы получить байесовский доверительный интервал, нужно то же самое просто подставить в первую формулу.

Плюс этого распределения в том, что оно имеет реализацию. Нам остается просто подставить значения и рассчитать. Для этого требуется всего несколько строк кода.

Рассмотрим, как это выглядит в динамике. Изначально мы запускаем сервис — неопределенность высока. Постепенно мы получаем данные, и интервал сужается.

Когда априорное распределение равномерное (т. е. мы ни в каких значениях не уверены), все это похоже на доверительный интервал. Однако важно помнить, что это принципиально другой взгляд. Правда, работать здесь можно точно так же — если бы наш интервал с байесовской точки зрения был далек от целевого значения, пора было бы паниковать. Также на графике представлен случай, когда априорно мы настроены чуть более скептично (красные интервалы). В итоге мы получаем похожую динамику в процессе набора данных, но наши интервалы смещены чуть ниже.

В рамках байесовского подхода мы подошли к задаче с другой стороны. На мой взгляд, здесь в большей степени выражается интуиция — мы вывели явное распределение на параметр M, не забыли о смещении, и это удобно. Результат получили схожий, хотя через совсем другую интерпретацию.

Использование биномиального распределения

Когда мы обсуждали частотный подход, то дополнительно рассмотрели схему с биномиальным распределением, в котором использовали в качестве статистики скорректированный TPR. То же самое мы можем сделать и в рамках байесовского подхода. Тут на самом деле еще проще в плане вывода. Напомню обозначения.

Теперь параметр \theta, который мы хотим оценить, это непосредственно TPR. Величина

n= FN + \frac{x}{100}TP

— размер выборки.

Величина

k= \frac{x}{100}TP

— количество верно отфильтрованных алертов в нашей выборке.

Тогда наше апостериорное распределение будет выглядеть следующим образом:

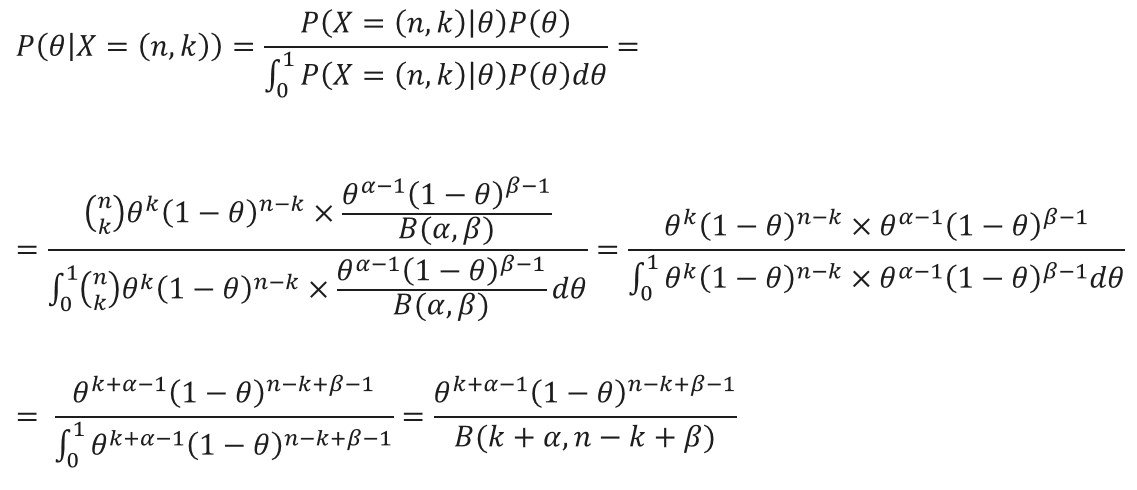
Итак, как вы могли заметить, здесь в качестве правдоподобия мы используем биномиальное распределение, а в качестве априорного распределения используем бета-распределение, которое в свою очередь является сопряженным априорным распределением, поскольку на выхлопе мы снова получили бета-распределение. Как я и обещал, здесь вывод распределения еще проще=)).

И снова весь байесовский вывод с его интегралами мы свели к простому пересчету параметров.

Аналогично посмотрим на байесовские доверительные интервалы в динамике.

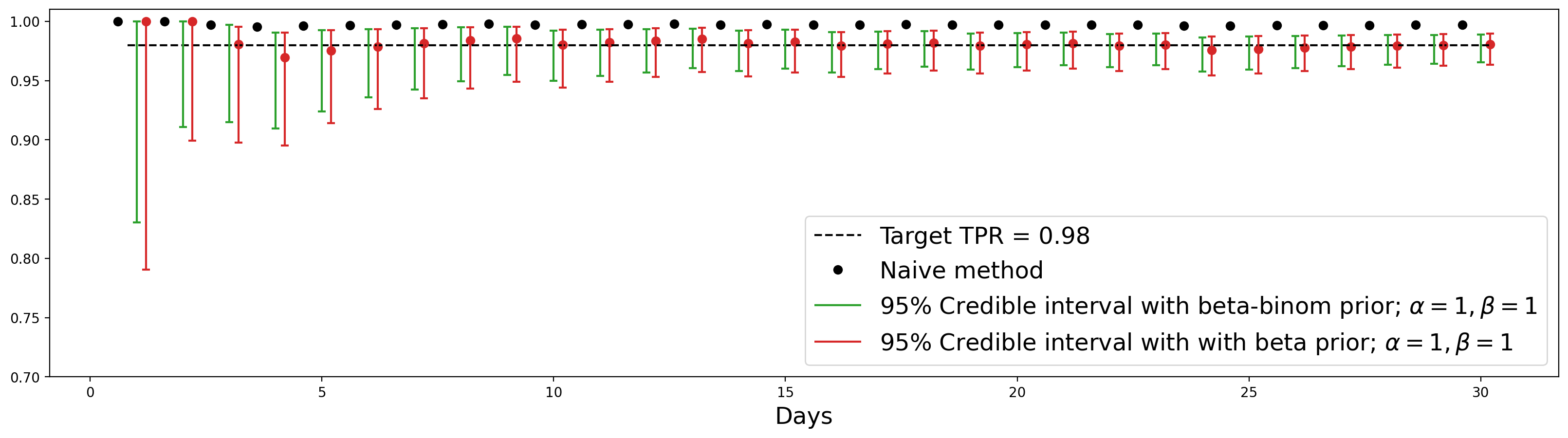
Здесь видим картину, похожую на ту, когда мы сравнивали частотные доверительные интервалы с разными распределениями под капотом. А именно, если мы используем биномиальное распределение, то интервалы получаются шире. Как мы уже разбирали, это соответствует тому, что мы накидываем нашу неопределенность еще и на будущие алерты.

Выводы

В этой статье я хотел показать, как мы решаем проблемы. На одну и ту же вещь можно смотреть с разных точек зрения даже внутри одного подхода (вспоминаем разные распределения под капотом). Мы привыкли сравнивать методы — что лучше, что хуже. Но в данном контексте выбор сводится к тому, как вам удобнее рассуждать и чем оперировать. Также выбор сводится к тому, а на какой вопрос вы хотите ответить с помощью статистики, неважно — байесовской или частотной. Конечно, стоит пользоваться именно тем, что ты хорошо понимаешь, потому что при решении задачи нужно оперативно интерпретировать результаты и донести их до других. А в таких проектах, как наш, умение понять и быстро объяснить результат является критическим :).

Если вам удобнее формулировать, что «с вероятностью 0,95 значение параметра лежит в данной области», выбирайте байесовский подход. Лично мне привычнее и интуитивно понятнее частотный подход, в рамках которого мы говорим, что «если будем повторять эксперимент много раз, с вероятностью 0,95 наш интервал будет накрывать истинное значение параметра». Именно поэтому в нашем проекте мы выбрали частотный подход. К байесовскому же подходу мы обращаемся тогда, когда с ходу неясно, как можно построить интервал с помощью частотного подхода, и нужно оценить поведение интервалов в динамике. Хотя признаюсь, что изначально я был большим фанатом байесовского подхода. Но со временем пришло осознание того, что не стоит себя ограничивать в рамках одного подхода или парадигмы. Ведь в конечном итоге у этих двух подходов одна цель — выразить с помощью математики нашу неопределенность.

Если вам интересны подобные задачи, если хочется погрузиться в недра построения моделей машинного обучения и благодаря этому строить безопасное будущее, приходите к нам в команду Data Science & Big Data. С помощью больших данных мы совершенствуем продукты компании и оптимизируем бизнес-процессы. У нас множество задач, связанных с контентной фильтрацией по категориям, которая в конечном счете помогает лучше справляться с угрозами безопасности. А если вам интересно копаться в описанных мной проблемах именно со стороны ИБ и противодействия атакам, то обязательно загляните к моим коллегам в подразделение Security Services, где открыты вакансии старшего SOC-аналитика, а также специалиста по реагированию на инциденты.

Комментарии (0)