В процессе обсуждения предыдущей статьи [1] не были замечены возможности конечных автоматов (КА), которых нет у других моделей. А, ведь, сами по себе КА не стоили бы такого большого интереса, если бы все сводилось только к отдельным автоматным алгоритмам. Это не умаляет достижений КА там, где они давно и заслуженно на ведущих ролях. Например, проектирование компиляторов. Но эти области достаточно специфичны, а речь идет об универсальном применении автоматной модели подобно модели блок‑схем.

Примером того, что к универсальному применению автоматов мы так и не приступили, хотя такие попытки были, может служить SWITСH‑технология[2]. Будучи весьма активной на начальном этапе своего развития, она со временем почти внезапно, по тихому схлопнулась и исчезла «с информационных лент». Может быть, у ее авторов пропала «мотивация к творчеству»? Я просмотрел текущие учебные планы университета ИТМО, выбрав дисциплину «Разработка программного обеспечения», но следов ни теории автоматов, ни автоматного программирования не обнаружил.

Тем не менее, работа в рамках SWITCH была проделана гигантская и материалов по автоматам на пока еще живом сайте доступно великое множество. Но надо признать, что в результате остался буквально... последний «выдох господина ПЖ». Вероятно, все потому, что больше внимания уделялось внешней форме автоматов, т.е. графическому их представлению, и специфике их реализации на базе операторов типа SWITCH, но совсем не рассматривались их уникальные качества. И было возникший интерес к автоматной теме так и не перерос в интерес практический. Даже в самом ИТМО.

И вот об этом — теории и практике современного автоматного программирования в контексте обсуждения предыдущей статьи хотелось бы поговорить, чтобы при последующих обсуждениях не возвращаться к определенным вопросам раз за разом.

О теории

Конечные автоматы и соответственно автоматное программирование (АП) интересны в первую очередь параллелизмом и эффективностью его реализации. Причем параллелизм у КА присутствует уже на уровне компонентного КА, но несомненно важнее параллелизм сетей автоматов. На примере простого алгоритма НОД было показано, как можно легко превратить любой алгоритм в процесс, а затем из них создать более сложную схему. «Сетевая конструкция» позволяет эффективно представлять параллельные процессы и создает понятную, простую и теоретически обоснованную теорию параллельных вычислений (см. подробнее [3]).

Модель отдельного КА определяет точки и механизмы взаимодействия (здесь вспоминаем про состояния) между параллельными процессами. Состояния автомата фиксируют моменты программного и/или аппаратного прерывания/приостановки/взаимодействия процессов (см. автоматный код НОД в статье). И не важно идет ли речь идет об имитации параллелизма в рамках одного потока или это будет множество потоков или даже ядер, т. е. того, что в иной подаче звучит как in parallel и concurrently. И здесь уже надо говорить об едином времени подобно единому времени реальных процессов. Соответственно, уточняя при этом, что на формальном уровне речь идет о сетевой автоматной модели с единым дискретным временем. При этом допускается, что разные сети вправе иметь индивидуальное дискретное время.

Дискретное время — важнейший элемент автоматной модели. Оно, как и состояния, зашито в определении модели. И уже только состояния и дискретное время выделяют автоматы на фоне других моделей. Дискретное время играет важнейшую роль в формировании качественно иной, например, по отношению к той же многопоточности или многоядерности, модели и теории параллельных вычислений. Важно также понимать, что любые асинхронные сети такой теории не имеют. Можно даже утверждать, что теория параллелизма на базе КА не была бы возможна без дискретного времени и, конечно, состояний. И актуальны они именно в своей «связке».

У других моделей аналогичной теории параллелизма просто не видно. Кто‑то наверняка упрекнет автора за эти слова. Убедите в обратном. Как бы то ни было, все это определяет ведущую роль автоматов по отношению к другим моделям. Ну а то, что пока нет широкой практической поддержки, то это лишь вопрос времени. В необходимости же теории параллельных вычислений, надеюсь, убеждать ни кого не надо.

Использование автоматов априори предполагает повышенную научную подготовку программиста. Кого‑то это наверняка сразу напряжет. Особенно занятых кустарным «увлекательным процессом подчинения компьютера». Но хотите или нет, но автоматы потребуют, как минимум, освежить знания во вполне определенных областях дискретной математики, и, как максимум, освоить теорию автоматов. Поэтому, когда кто‑то с апломбом ли, в шутку ли или, тем более, всерьез высказывает пренебрежение к подобной математике, то это только отражает уровень квалификации и узость его интересов (это ответ одному из авторов подобной «идеи», высказанной по ходу обсуждения исходной статьи).

Теорией автоматов нужно пропитаться. Другого варианта не существует! Если что‑то не ясно — ищите ответ в теории. Сомневаетесь в чем‑то — ищите ответ в теории. Не знаете как поступить — ищите ответ в теории. Не нужно шарахаться от слов «теория автоматов», «конечный автомат», «сеть автоматов». При этом на уровне обычного пользователя эти понятия объясняются достаточно просто. Главное не искажать их диаграммами Харелла, автоматной моделью UML, MATLAB‑а или чем‑то подобным.

Все, что нужно знать об автоматах для их практического применения и даже чуть больше (типа умножения автоматов), описано автором на Хабре, рассмотрено на примерах, даны ссылки на нужную литературу. Этого более чем достаточно, чтобы «подковаться» и эффективно использовать автоматы практически. Хотите больше — теория множеств, булева алгебра, теория автоматов — вам будут в помощь. Без этих знаний обсуждать что‑то почти невозможно. А начинать обсуждение с ликбеза, что часто приходится делать, тоже не выход, т.к. общение вязнет уже на этом этапе.

Конечный автомат — это цикл

Утверждение, вынесенное в заголовок, является довольно распространенным. Кто его первый произнес, наверное, уже не выяснить, но оно постепенно превратилось в своеобразную мантру. Однако циклов, сравнимых циклами блок‑схемам, у автоматов, безусловно, нет. Но у автоматных графов могут быть циклические пути.

Можно возразить, что блок‑схема — тот же граф, в котором циклы это те же циклические пути. И это справедливо. В блок‑схемам циклические пути реализуются циклическими операторами языков программирования. Это всем известные операторы типа WHILE, FOR или их заменяющие связки управляющих операторов. Но есть существенный нюанс — выйти из цикла блок‑схемы можно или 1) по условию его завершения или 2) принудительно с помощью оператора типа breack или того же goto. Но, например, для последователей структурного программирования использование последних просто неприемлемо. В результате всегда сохраняется опасность попадания в бесконечный цикл. А это особенно критично, если процесс локализован в пределах одного потока.

Но все же решение описанной выше проблемы существует. Это аппаратное прерывание текущего программного потока. В этом случае даже бесконечный цикл не окажет фатального влияния на другие потоки. Они будут работать как будто ни чего не случилось. Но в подобном многопоточном программировании есть множество проблем — непредсказуемость, недетерминированность и сложность механизмов синхронизации и взаимодействия многопоточных программ.

Другое решение — сопрограммы. Нынче они представлены корутинами. Но по сравнению с многопоточностью это все же существенно менее гибкое решение. И здесь тоже есть беда: из цикла вы сможете выйти, но могут быть проблемы с обратным возвратом, т. е. опасность зависания не устраняется. Можно сказать, если у многопоточности излишняя гибкость, то у сопрограмм — прямо таки жестокая ограниченность.

У автоматов прерывание программного процесса организуется при смене состояний. И если при многопоточности переключение происходит в непредсказуемом месте и в непредсказуемое время, то у автоматов все происходит ровно тогда, когда это необходимо. И пример автоматного кода НОД это демонстрирует. Так повышает эффективность реализации параллелизма. Все происходит в предсказуемые моменты и может быть просчитано формально на базе операции композиции. Более того, можно вспомнить, что современное программирование давно усиленно решает и ни как не может решить проблему автоматического распараллеливания. Для автоматов это делается «по щелчку» — разбиением отдельного процесса с помощью операции декомпозиции.

Итак, автоматам, казалось бы, циклы не грозят от слова совсем. Но поскольку предикаты и действия реализуются как обычные функции, то они‑то могут быть зациклены. Но тело подобных функций, как правило, достаточно компактно и их циклы легко контролируемы. В конце концов их также можно перевести в автоматную форму. Это, правда, увеличит время работы, но здесь надо выбирать — между надежностью и скоростью работы. В то же время, если цикл не очень большой, то пользователь изменений в скорости может попросту не заметить. Более того, разбивая неделимое тело достаточно длительного по времени действия из‑за цикла, мы уменьшаем время отклика приложения. Напомним, что реально длительность дискретного такта определяется суммарной длительность всех предикатов и действий автоматов, задействованных при его реализации.

О проблемах SimInTech

Причем здесь опять среда SimInTech? Помимо почти полного совпадения ее внутреннего языка программирования с языком Н.Вирта, она в силу специфики своей реализации подходит для наглядного рассмотрения описанных выше проблем. Например, если бы в ней каждый блок был реализован в своем потоке, то мы бы их просто не заметили. Может, изменилось бы реальное время расчета, но обрушения приложения не было бы. А так проблема зацикливания в SimInTech проявила себя в полной красе.

Зависание среды было, безусловно, было следствием имеющейся в алгоритме ошибки. Сделал ли ее автор или Н. Вирт — не столь уж принципиально. Тот же Н. Вирт подчеркивает, что проблема программных ошибок потенциально неизлечима. В этом смысле, перефразируя Н. Вирта, можно даже сформулировать следующее правило:

Экспериментальное тестирование программ может служить доказательством наличия циклов, но не доказывает их безопасность.

Реализация блоков в SimInTech на базе автоматной модели не гарантирует правильности результатов. Это почти сразу при тестировании схемы из блоков НОД и было обнаружено. Но автоматы могут служить гарантом от обрушения приложения. Кроме того, решение, созданное на базе автоматной модели, точно отражает временные свойства блоков. Обычная реализация эти процессы, наоборот, искажает. Это все вполне убедительно и наглядно отражают приведенные в статье графики.

Следует ли считать запуск блоков на каждом дискретном шаге среды программным циклом? Конечно, нет. Аналогию можно провести с реальным процессором. Каждый процессор содержит тактовый генератор, но не все программы в силу этого считаются циклическими, а только лишь те, которые явно содержат операторы цикла. Так и в случае автоматов. Те, которые содержат циклические пути, безусловно, можно считать циклическими, но все же отличие в реализации циклов в блок‑схемах и автоматах оказывает на подобную работу свое существенное влияние.

Выводы

Могут ли автоматы, содержащие циклические пути, обрушить приложение? Реализованные определенным образом, но только не так, как в это показано в обсуждаемой статье, — не вопрос. Зациклить — пожалуйста. Исказить результат — без проблем. Но приложение не зависнет, а отработает заданное в настройка время. А уж дальше нужно сделать правильные выводы из анализа полученных результатов и внести необходимые корректировки в алгоритмы работы блоков.

На рис. 1 показаны графики работы автоматных блоков с ошибкой и без нее. Наличие ошибки явно отражается на виде графиков(см. на рис. 1 красный график). Исправив ошибку, мы получаем нужный нам результат.

И, опережая предполагаемые вопросы, объясним вид графиков: в настройках задан шаг равный 0.01 при общем времени расчета — 0.3 сек. Это растягивает внешний вид графиков.

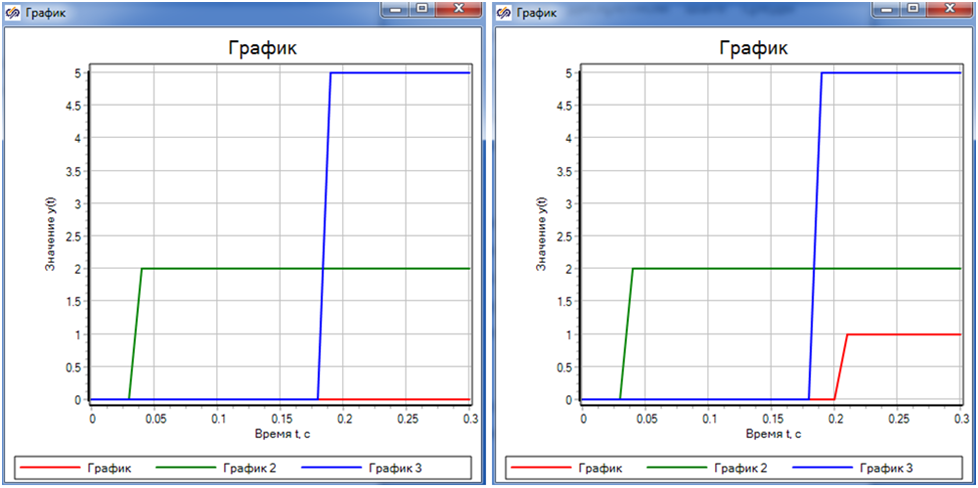
Изменив значение шага проекта на 0.0001, мы получим уже иной их вид (см. левый график на рис. 2):

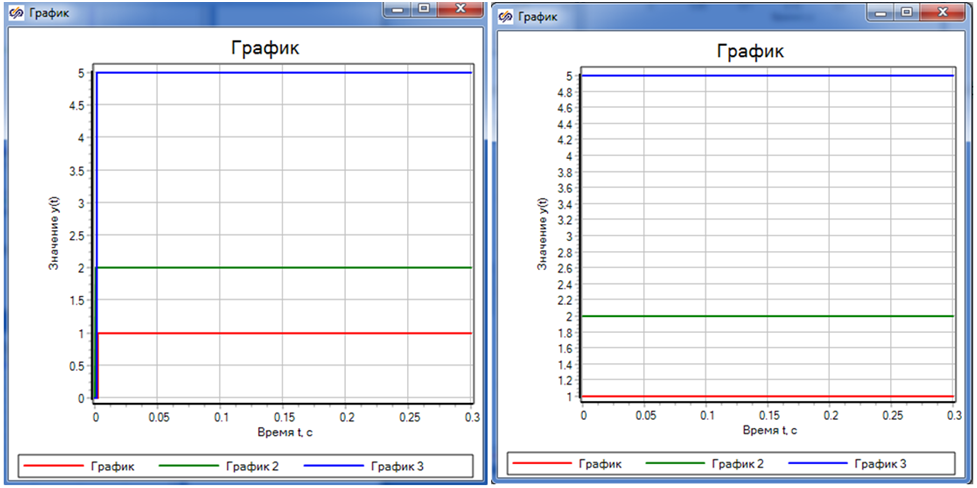
Справа приведен график на базе обычных блоков. Он не меняет свой вид даже при значительном изменении значения дискретного шага. Можно также видеть, что в сравнении с левой диаграммой на диаграмме справа красный график почему‑то смещен вниз. По нашей версии это объясняется пресловутой «мгновенностью» блоков в SimInTech. Но точно на этот вопрос могут ответить лишь разработчики среды. Более же красочно и «сочно» объяснить причины этого смогут пресловутые «суровые сибирские мужики»...

Литература

1. Об ошибке Вирта и вреде операторов цикла. [Электронный ресурс], Режим  доступа: https://habr.com/ru/articles/746674/ свободный. Яз. рус. (дата обращения 11.07.2023).

2. Сайт по автоматному программированию и мотивации к творчеству.  [Электронный ресурс], Режим  доступа: https://is.ifmo.ru/ свободный. Яз. рус. (дата обращения 11.07.2023).

3. Модель параллельных вычислений. [Электронный ресурс], Режим  доступа: https://habr.com/ru/articles/486622/ свободный. Яз. рус. (дата обращения 11.07.2023).