
Добрый день, уважаемые хабровчане.
Примерно год назад я начал проект симулятора динамики частиц на Python, используя библиотеку Numba для проведения параллельных расчетов на видеокарте. Сейчас, добравшись до определенной вехи в его развитии, я решил открыть исходный код и выложить его на GitHub для всех, кому интересны подобного рода эксперименты.
Самостоятельно потыркать проект можно вот тут: https://github.com/r-aristov/simba-ps
В этой статье я кратко опишу суть проекта, пройдусь по прилагающимся к нему примерам и расскажу, почему вообще начал работу над ним.
Да кто такие эти ваши Леннард и Джонс?
На самом деле, это не два разных человека, а один - Сэр Джон Леннард-Джонс, который сотню лет назад придумал относительно простую физическую модель взаимодействия точечных частиц. Физически она задает потенциальную энергию взаимодействия пары частиц в зависимости от расстояния между их центрами.
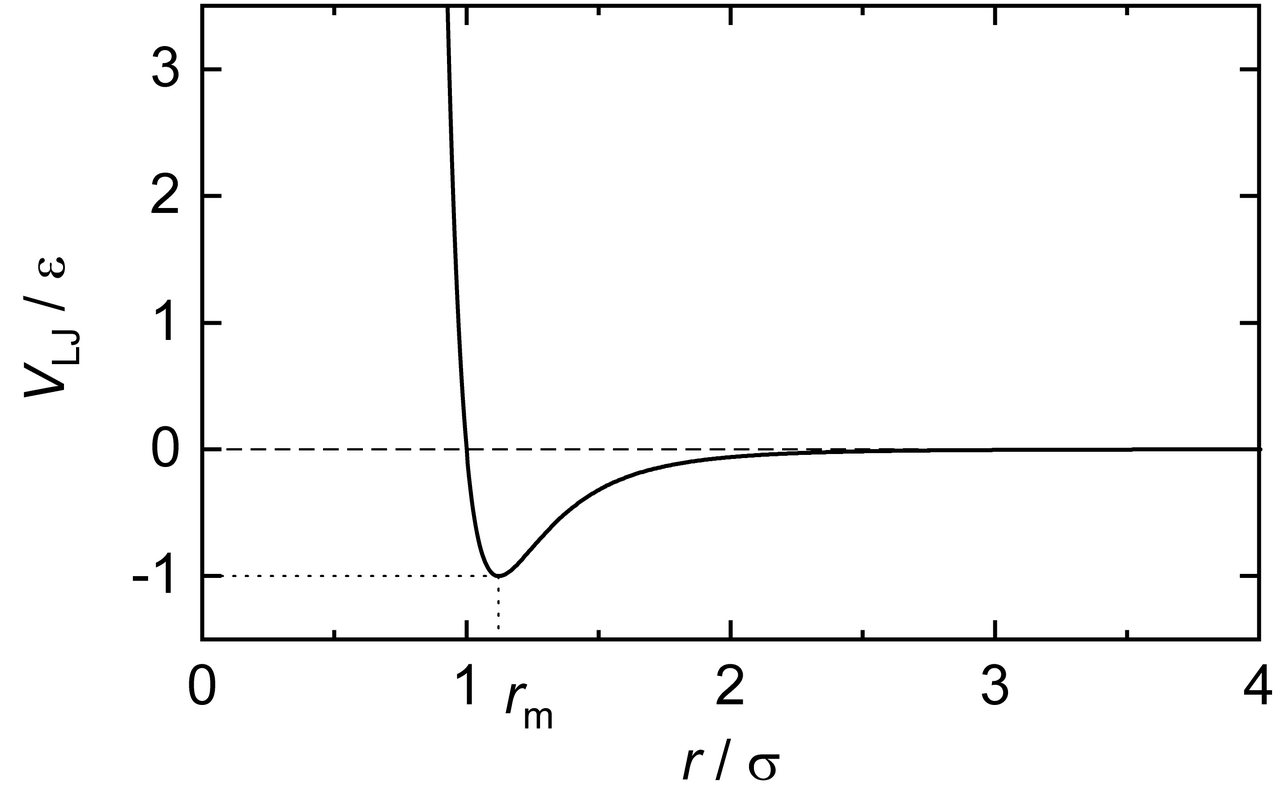
Как таковых радиусов у частиц нет, они представлены не шариками в пространстве, а именно точками, у которых есть координаты и скорость. Вместо этого сам потенциал имеет два параметра - глубину потенциальной ямы, задающую минимальную энергию, которой могут обладать взаимодействующие частицы, и расстояние
, на котором должны находиться частицы, чтобы этой минимальной энергией обладать.
В нуле потенциал улетает в бесконечность, не позволяя частицам пролетать друг через друга, по крайней мере, так это выглядит в идеальном мире теоретических расчетов. В численной симуляции, разумеется, все зависит от реализации - эта бесконечность в точке 0.0 порождает всякие забавные ситуации, в которых быстрые частицы влетают друг в друга с такой энергией, что начинают туннелировать прямо сквозь соседей, причем это сопровождается бесконтрольным ростом их и так немалой кинетики, из-за чего симуляция "взрывается".
Впрочем, об этих особенностях я подробнее расскажу в следующих статьях. По форме этого потенциала можно заметить, что он обеспечивает не только отталкивание чересчур сблизившихся частиц, но и притяжения на малых расстояниях - это именно то, что отличает его от простой реализации отталкивающихся "бильярдных шариков" - благодаря притяжению частицы не просто разлетаются в стороны, а формируют макро-структуры, которые можно заметить на гифке из заголовка. Кстати, в readme репозитория есть эта и другие гифки в куда более приятном глазу качестве.
А что он может?
Именно за счет этого двойного действия (притяжения на одних расстояниях и отталкивания на других) одна эта простая формула порождает удивительное множество эффектов, которые могут быть промоделированы относительно простым кодом. Все, что нужно - это продифференцировать ее по переменной , чтобы получить величину силы, действующей на частицу (ведь как мы помним - сила - это минус производная от потенциала!), написать сносный численный интегратор, что-нибудь сделать с квадратичным ростом количества взаимодействий, чтобы видеокарта не расплавилась от натуги, и как следует это все распараллелить для вычисления на GPU. И чтобы вам не пришлось этим заниматься, я это сделал за вас в своем симуляторе Simba (что означает Simulation with Numba).
Это - первая обзорная статья, поэтому тут я не буду вдаваться в глубокие подробности реализации. Если заинтересует - распишу все это в последующих материалах. Скажу только, что я реализовал интегрирование Вереле [Verelet], а также для эксперимента - Рунге-Кутту и некий интегратор Йошиды, но последние два не вошли в релиз, так как показали себя хуже стандартного Вереле. Чтобы распараллелить вычисления и избежать квадратичного роста вычислительной сложности я использую то, что в зарубежных материалах называется hash-grid. Я предпочитаю называть это "enforcing locality" - информация о частицах сохраняется в 2д карте в соответствии с их позициями, этим мы как бы принуждаем взаимодействия к локальности, каждая частица при расчете сил смотрит только на небольшую область вокруг себя и берет информацию об окружении из этой 2д карты. А так как видеокарты позволяют проводить расчеты в тысячи потоков, каждая частица, по сути, обсчитывается независимо от других.
Итак, что же можно моделировать при помощи потенциала Леннарда-Джонса и Симбы в частности?
Виртуальная химия
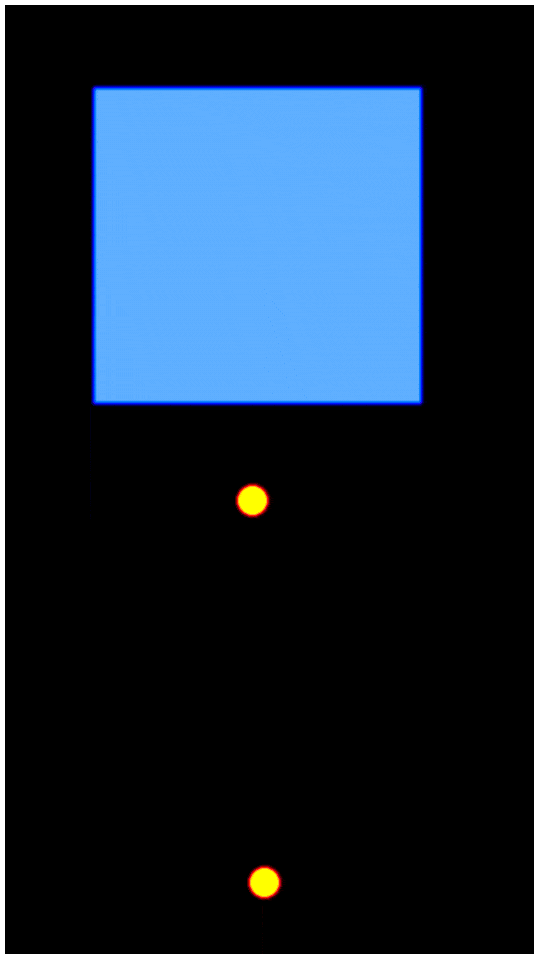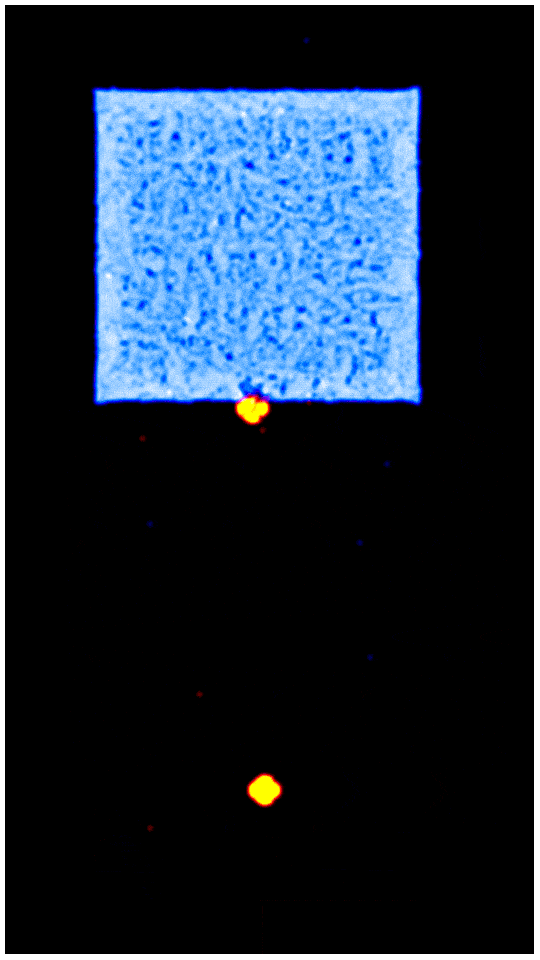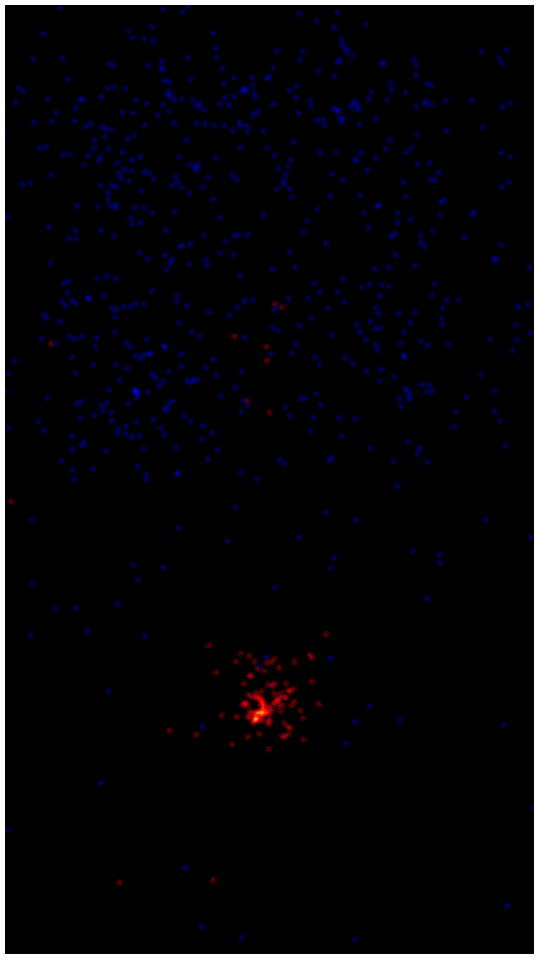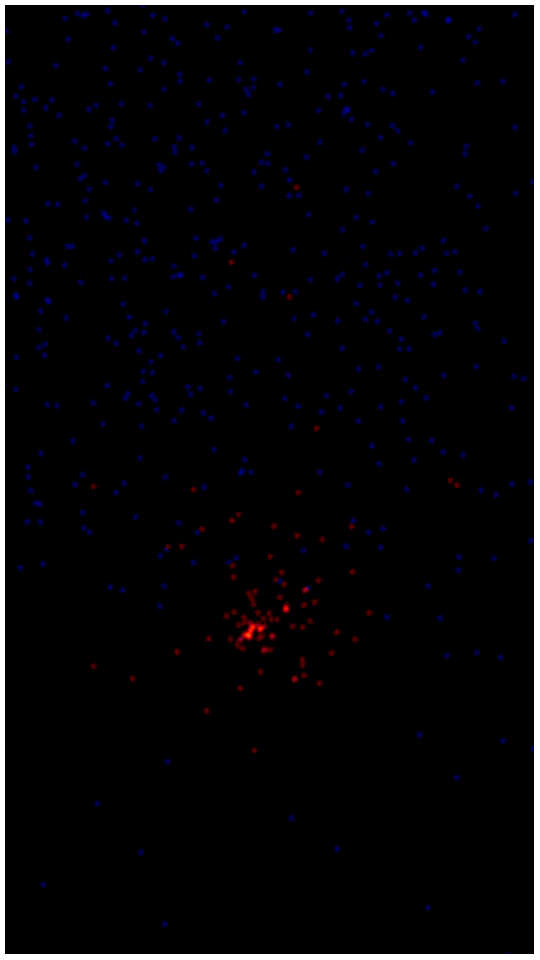
Ну, например, можно вместо одного типа частиц сделать четыре, и для каждой возможной пары взаимодействующих типов частиц задать свои значения глубины потенциальной ямы и оптимального расстояния. Это приведет к тому, что частички будут взаимодействовать друг с другом по-разному, формируя молекулы. Вот, например, симуляция экзотермической реакции, в которой изначально есть два типа молекул - красно-синие и зелено-желтые. И те и те состоят из 5 частиц, одной синей в окружении четырех красных и одной желтой в окружении четырех зеленых. Это достаточно стабильная конфигурация, а красные с зелеными не особо взаимодействуют, поэтому эти молекулы просто легонько отталкиваются друг от друга, оставаясь целыми. Но связь желтой частицы с синей на несколько порядков более энергетически-выгодная, чем все остальные! Поэтому достаточно лишь легкого толчка, чтобы началась самоподдерживающаяся экзотермическая реакция. В видео в качестве такого толчка выступает несколько свободных желтых частичек, одну из которых я пинаю в сторону красно-синей молекулы. Не будучи окруженной экранирующими ее зелеными частицами, она стремиться провалиться в глубочайший потенциальный колодец синей частицы, разрывая красно-синюю молекулу на части.
Кстати, если фраза "в реакции выделяется энергия" вам всегда казалась туманной, то вот - это именно так и происходит. Стремясь занять более энергетически выгодное положение, частицы разрывают стабильные молекулы и их осколки с огромной скоростью летят во все стороны, разбивая все новые молекулы и открывая высокоактивные желтые и синие частички для новых реакций.
А если эту смесь потом охладить, они начинают слипаться в длинные полимерные цепочки.
Это, наверное, наиболее интересное видео из категории "виртуальная химия", остальные помещу под спойлер.
Еще виртуальная химия
Леннард-Джонсовский самогон
Перейдем из микромира в макромир. Всё той же формулой описываются и газы, и жидкости и твердые тела. Разница только в том, какова глубина потенциальной ямы и какова энергия частиц - хватает ли ее только на колебания около оптимального положения, или частицы могут вылететь за пределы этих связей. А это значит, что "леннард-джонзиум" (так иногда зовут это виртуальное "вещество") можно кипятить и замораживать, и он будет менять свое состояние в соответствии с самой настоящей фазовой диаграммой. Но не будем его кипятить просто так, лучше будем перегонять в виртуальном перегонном кубе!
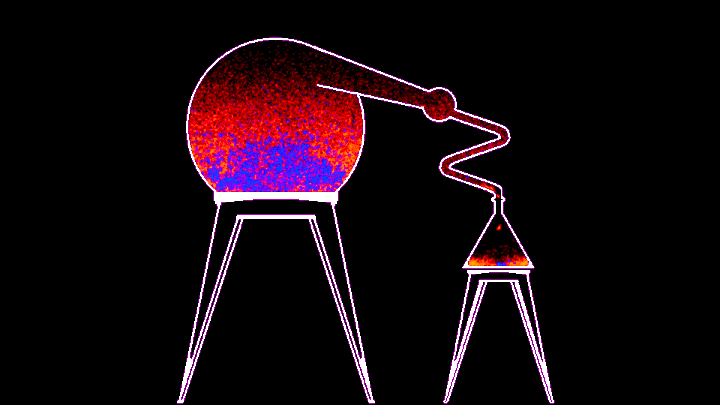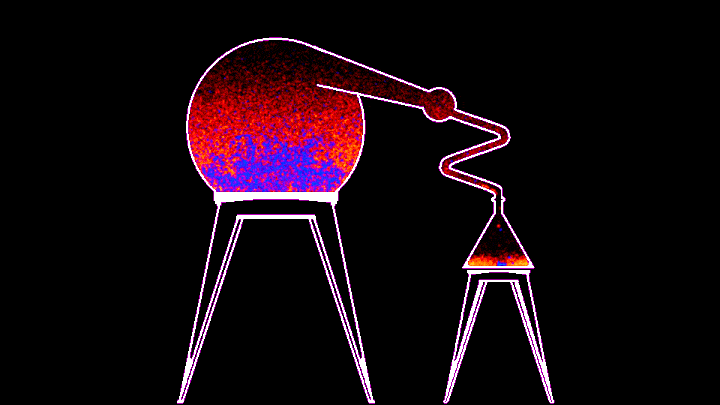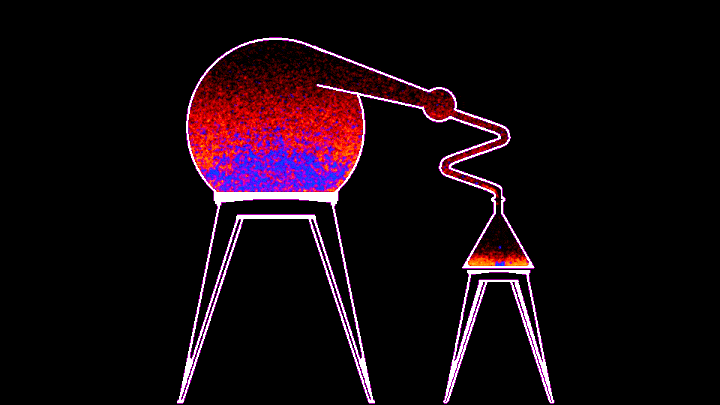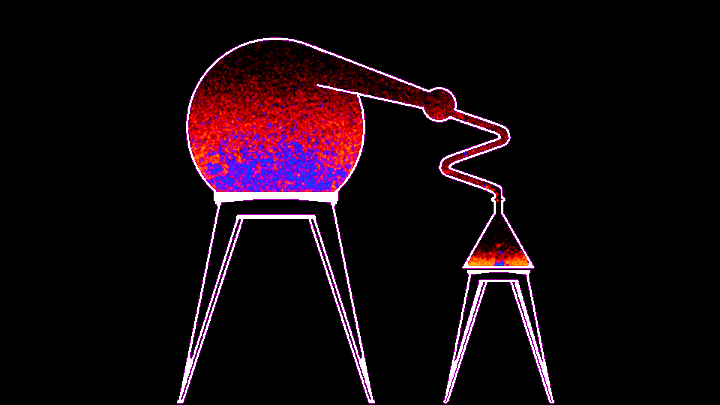
Процесс, к сожалению, не очень быстрый - гифка ускорена в 10 раз, но из этого, на мой взгляд, могла бы получиться неплохая механика для игры про алхимию. В примере, который идет вместе с симулятором, можно менять температуру нагревателя из командной строки, а в самом коде можно поменять энергию связи красного и синего веществ (то бишь глубину потенциальной ямы). По дефолту у синего вещества она в 14 раз больше, значит его частицам надо в 14 раз больше энергии, чтобы вылететь за пределы потенциальной ямы, поэтому первым испаряется красное. В змеевике расположен виртуальный термостат, охлаждающий пролетающее через него вещество, из-за чего оно конденсируется и капает в колбу.
Процесс с самого начала и до конца показан в видео
Правда, в этом видео еще прошлый вариант установки, чуть менее эстетичный, поэтому к релизу я ее перерисовал.
Кстати, самое время сказать о том, как происходит конфигурация симулятора. На вход идет буквально картинка из пеинта - в самом начале разработки я решил, что так мне будет проще всего - не надо городить какой-то особый редактор, просто рисуешь в пеинте картинку, а в коде буквально парой строк задаешь соответствие цвета из картинки параметрам частиц. Белый цвет воспринимается как пустое пространство, любой другой можно использовать в соответствии со своими замыслами. Симуляция столкновения, как в заголовке, например, требует входной картинки (или можно, при желании, разместить частицы кодом) и строк 10 кода, половина из которых - это настройка камеры и рендера. Для симуляции дистилляции нужно все то же самое, плюс еще пара строк, задающих работу термостатов.
Детерминистический хаос
Одна из моих любимейших тем в исследованиях. Хаотические и детерминистические системы, в которых можно воочию увидеть, как может процесс быть одновременно детерминистическим, непредсказуемым на практике и меняющими траекторию в своем фазовом пространстве при микроскопических, едва заметных изменениях.
Симба - детерминистический симулятор. Ну, то есть, это можно включить параметром deterministc=True. А это значит, что можно прогнать симуляцию, потом присвоить, скажем, цвета частичкам в соответствии с их финальным положением, а после запустить симуляцию заново и смотреть, как из хаоса рождается картинка.
Это, кстати, работает как неэффективная, но прикольная криптография. В том смысле, что эта система невероятно чувствительна к начальным параметрам - достаточно поменять буквально любой параметр любой из частиц (позицию, скорость) даже на одну десятимиллиардную, и картинка уже не сложится. Тут в качестве зашифрованного сообщения выступает информация о том, какие цвета какой частичке были присвоены, а в качестве ключа - любой набор любых параметров начального состояния. Более подробно весь процесс показан в видео под спойлером. И там же еще пара видео на этом же эффекте, которые я отрендерил, работая над детерминизмом Симбы.
Окунитесь в детерминистический хаос
Кстати, это оказалось не такой уж тривиальной задачей - это в школьной арифметике от перемены мест слагаемых сумма не меняется, а в суровой взрослой жизни операция сложения чисел с плавающей запятой неассоциативна из-за конечной точности представления. А это значит, что если мы будем, скажем, общую силу, действующую на частицу, считать параллельно и просто прибавлять ее компоненты к какому-то аккумулятору, результаты будут отличаться от запуска к запуску - видюха-то считает вразнобой, порядок каждый раз разный. Но этот эффект можно победить. В целом, даже без какого-либо ощутимого оверхеда, но я все равно сделал детерминизм отключаемым, на всякий случай.
Чтобы не захламлять статью, не буду сюда перекладывать гифки из ридми на гитхабе, тем более, что они весьма тяжелые - алгоритмы сжатия с большим трудом прожёвывают такие картинки из-за огромной энтропии теплового движения частиц. Там есть еще несколько примеров, чуть более простых, чем перечисленные тут - столкновение, которое я вынес в заголовок поста, оно же, но с другой визуализацией, без сглаживания, зато с цветом частиц, соответствующим величине их вектора скорости, разноцветные частички в ячейках, отличающиеся температурой...
Еще Симба вполне тянет несколько десятков тысяч частиц в реалтайме, так что можно его использовать как часть игрового движка. У меня на ютуб канале есть пара видео с реалтаймовыми экспериментами. В релиз такие примеры вкладывать уже не стал, но запустить симулятор в таком режиме - задача тривиальная, любой знакомый с PyGame или с разработкой оконных приложений, справится с этим без труда.
Осталось ответить на главный вопрос.
Зачем все это?
Ну, во-первых - это прикольно. Меня завораживает сама идея того, что из одного простого уравнения (из двух, если считать закон Ньютона) может вырасти система, обладающая таким широким спектром разнообразных свойств - тут тебе и жидкости, и газы, и дистилляция, и воронки, и детерминистический хаос. У меня даже получилось из этого джонзиума буквально выплавить струну - вот прямо "залить" его в форму и охладить, чтоб частички заняли оптимальное положение - и она звучала! Хреново звучала, постоянно рвалась, но все-таки.
Я давным-давно хотел этим заняться, и вот год назад решил, что no time like the present, и что откладывать так можно вечно, и если я этим не займусь, то так и не увижу то, что хотел увидеть реализованным. Ну, а выложил код я чтобы те, кому это так же интересно, могли сразу поэкспериментировать. Как говорится, я потратил год на этот код, чтобы вам не пришлось.
Во-вторых, мне вот всегда было интересно - а паровую машину так можно сделать?
Оказалось - можно.
Здесь Симба отвечает за частицы и поршни, а физику маховика и кривошипно-шатунного механизма я прикрутил сверху, в питоне, но это не единственный вариант)
Я не стал пихать этот код в релиз, потому что, честно говоря, его надо бы еще тестить и оптимизировать, а у меня сейчас другие дела, но я-таки реализовал физику твердых частиц прямо внутри симулятора. А это значит, что эту паровую машину можно построить из частичек прямо целиком. А еще всякие ракеты с разными формами сопел, пробки, вылетающие под давлением из бутылок и тому подобное. Под спойлером видео с примерами таких экспериментов.
Физика твердых тел и частиц в Симбе
Ну и наконец, главная причина, которую я приберег напоследок. На самом деле, я уже давно занимаюсь машинным обучением, и больше чем детерминистический хаос люблю только нейронные сети (которые, кстати, будучи нелинейными системами, тоже демонстрируют такое же поведение). Мне всегда было интересно, какие знания и как можно дистиллировать в коэффициенты современных сеток. Получится ли обучить ее динамике частиц? А как будет выглядеть выход за установленные пределы по энергии - обычная симуляция просто взрывается, а как себя поведет сеть? А можно ли "на дурачка" промоделить жидкости на уровне частиц, а в сетку дистиллировать знания об их усредненном поведении, чтобы она сама вывела внутри себя аналог уравнений CFD (computational fluid dynamics, уравнений динамики жидкостей), и потом использовать для симуляции уже ее, не симулируя сотню тысяч частиц? Так как симулятор реализован на чистом Питоне, он элементарно стыкуется хоть с PyTorch, хоть с Tensorflow, и позволяет построить быстрый и эффективный пайплайн для обучения.
Не так давно я добрался до значимой вехи в этом проекте и-таки обучил сетку считать физику частичек вместо Симбы.
После этого я и стал готовить опенсорсный релиз симулятора. Сейчас релиз готов, а это значит, что я возвращаюсь к своим исследованиям и с радостью буду делиться с вами дальнейшими результатами.
На этом у меня все, подписывайтесь на мой телеграмм-канал, где я делюсь рабочими моментами исследований и просто заинтересовавшими меня вещами, а также на мой ютуб-канал, куда я выкладываю свои визуализации экспериментов. Хорошего вам дня!
Комментарии (70)

Qvxb
17.07.2023 17:38Как таковых радиусов у частиц нет, они представлены не шариками в пространстве, а именно точками, у которых есть координаты и скорость.
Я так понимаю "массы" у частиц нет, т.е у летящей частицы скорость просто падает когда она подлетает к покоящейся, с другой стороны оно так и задумано судя по всему.
Кстати вот такая формула для нового значения скорости:
new_v = v + dt * 0.5 * (a + new_a)
а зачем в ней 0.5?
Еще вопрос: dt наверное равен времени кадра в мс?
Ariman Автор
17.07.2023 17:38+3Нет-нет, масса есть, конечно. Потенциал отвечает за действующие силы, а ускорение из этих сил считается, как обычно, a = F / m.
А 0.5 там потому что так устроено это интегрирование Вереле - по сути этот интегратор говорит "Между дискретными отсчётами будем считать, что всё происходит равноускоренно/равнозамедленно", то есть, под действием постоянной силы. В качестве этого ускорения берется средняя величина между ускорением в прошлом отсчёте и новым, посчитанным из сил на этом шаге. Отсюда и 0.5)
dt - это время между отсчётами, да. Но это не совсем время между кадрами, на каждый кадр идёт N под-шагов. Величина N зависит от энергий в симулируемой системе. Это одна из поразительных вещей, вроде и простая, но не сразу очевидная: виртуальная энергия не "бесплатная", нельзя просто так взять и добавить энергию в столкновение, например - за нее придется платить возросшими затратами реальной энергии, идущей на вычисления, потому что придется делать больше шагов интегрирования. Иначе "бомбанет")

Qvxb
17.07.2023 17:38А 0.5 там потому что так устроено это интегрирование Вереле - по сути этот интегратор говорит "Между дискретными отсчётами будем считать, что всё происходит равноускоренно/равнозамедленно",
А для позиции выбран обычный способ:
d_pos = v * dt + (0.5 * dt ** 2) * a
positions[idx, c_idx] = positions[idx, c_idx] + d_pos
а почему бы не использовать метод Верле и там и там?Нет-нет, масса есть, конечно. Потенциал отвечает за действующие силы, а ускорение из этих сил считается, как обычно, a = F / m.
Ясно, а что происходит с "энергией" которой обладают движущиеся частицы?
она как то учитывается при взаимодействии?
Ariman Автор
17.07.2023 17:38+1Это и есть "Метод Вереле", все целиком. Тут нет двойного интегрирования, в смысле, это не то что мы сначала применяем этот интегратор к x'' получая x', а потом к x' получая x. Вместо этого позиция считается напрямую, как если бы тело двигалось под действием постоянной силы. Мы сразу получаем точное (ну, в пределах точности метода) приращение координат.
Не очень понял вопрос - в каком смысле, что происходит с энергией? Частицы обладают потенциальной энергией из-за своей позиции в потенциале Леннарда-Джонса, она меняется вместе с изменением их координат. Еще они обладают кинетической энергией, которая половина квадрата скорости помноженная на массу. Она меняется вместе с изменением скорости при движении частицы в направлении минус градиента потенциала - как и положено, они друг в друга перетекают и их сумма для всей системы даже более-менее остается постоянной, за вычетом дрифта из-за неточности интегрирования. Если шагов интегрирования мало, а энергии столкновений большие, то этот дрифт становится больше. Если очень большие, то он начинает расти с каждым отсчетом и симуляция "взрывается".

azTotMD
17.07.2023 17:38она как то учитывается при взаимодействии?
учитывается - чтобы приодолеть отталкивание соседней частицы нужно обладать достаточной энергией, приближаясь всё ближе частица замедляется силами отталкивания, при этом потенциальная энергия взаимодействия - растёт. Без термостатов сумма этих энергий - константа. С термостатами будут колебания.

enclis
17.07.2023 17:38"all-Python" не тоже самое, что и "чистый Python".

Ariman Автор
17.07.2023 17:38А в чем разница? В том, что тут дергается нумба, которая из части этого питона собирает код для GPU?
Ну, я подходил с практической точки зрения - "чистый питон" в том смысле, этот код можно сразу пристыковать к любому питоновскому ML-пайплайну, не городя никаких "переходников", ничего не перекомпиляя и т.п.

Inobelar
17.07.2023 17:38Оффтоп: детерминизм симуляции у вас, напомнили мне похожее видео. Идея использования этого для криптографии тоже интересная - по сути это простой алгоритм, но с ооочень длинным ключом (состоянием).

Ariman Автор
17.07.2023 17:38+4Да, я подписан на этого товарища. Но мое видео вышло раньше) Впрочем, я думаю, что у любого, кто закодил физику частиц, независимо ни от кого возникает желание заставить их падать, складываясь в картинку)

Dancho67
17.07.2023 17:38+2Эх, на такой либе, написать бы продолжение Powder Toy. В свое время не один вечер убил, экспериментируя с разными материалами в попытках добиться чего-то впечатляющего.

Travisw
17.07.2023 17:38Не хватает немного объяснение теории как взаимодействуют частицы в столкновении и как действует гравитация со схемами

ris58h
17.07.2023 17:38+1Выглядит круто!
Только ссылки бы на рускоязычную Википедию давать (соответствующие статьи в большинстве случаев там есть) - статья на русском всё же.

phenik
17.07.2023 17:38+3Мне всегда было интересно, какие знания и как можно дистиллировать в коэффициенты современных сеток. Получится ли обучить ее динамике частиц? А как будет выглядеть выход за установленные пределы по энергии — обычная симуляция просто взрывается, а как себя поведет сеть? А можно ли "на дурачка" промоделить жидкости на уровне частиц, а в сетку дистиллировать знания об их усредненном поведении, чтобы она сама вывела внутри себя аналог уравнений CFD (computational fluid dynamics, уравнений динамики жидкостей), и потом использовать для симуляции уже ее, не симулируя сотню тысяч частиц?
Возможно вы в курсе этой публикации (оригинал), где решается даже боле сложная задача, и обучение производится не на симуляциях, а на эмпирических данных, что логичнее. Задача состоит в оценке размерности сложных динамических систем, которые пока не описываются аналитически, путем обучения на более простых, описание которых уже известно. А эта система сама выводит законы из эмпирических данных. В этой работе исследуются некоторые методические сложности применения обучения нейросетей для вывода физических законов из эмпирическим данным и предлагается вариант их решения.
Что касается обучения на физических симуляциях, то подобное делается давно, например, для задачи трех тел. Эта работа посвящена классификации рассеяния ионов. Использование МО для решения физических задач устойчивый, быстро растущих тренд в физических исследования, а астрофизических носит просто взрывной характер, из-за наблюдательной специфики области.
Возможно также слышали о работах Ванчурина, который вместе с соавторами, вообще вознамерился свести всю физику, включая фундаментальную, и космологию к обучению нейросетей (1, 2, 3, популярно 4, 5, видео). Вот такие дела)
Не исключено будущее именно за такими методами исследования и описания в прикладной и фундаментальной физике, из-за возрастающей сложности объектов исследования, результаты которых невозможно будет свести к традиционным аналитическим моделям. А если и удастся, то для их решение для реальных систем из многих частиц может не хватить никаких вычислительных ресурсов, см., например, лагранжиан СМ. Только приближенные, использующие упрощающие предположения и удовлетворяющие некоторым критериям точности. Но это та область в которой решение задач с помощью обучения нейросетей представляется очень эффективным методом.
Спасибо автору за публикацию и удачи в поисках!

Ariman Автор
17.07.2023 17:38+2и обучение производится не на симуляциях, а на эмпирических данных, что логичнее
Смотря для какой задачи логичнее) Например, я упоминал в комментариях выше, что подход "обучить на медленной симуляции быструю сеть, чтобы после использовать ее вместо симулятора" тоже очень распространен.
Да, я в курсе, что такие исследования проводятся и это теоретически возможно на самых разных уровнях реализации. Но, как в том фильме - "Винтовок много, но эта - моя") как правило в таких задачах огромное количество "подвижных частей", столько всего можно реализовать по-разному, столько тонкостей, которые влияют на результат и которые в статьях обычно опускаются.
Мне интересно именно посмотреть, что получится на практике конкретно у меня, с моими ресурсами, конкретно на тех задачах, которые интересуют меня.
Про Ванчурина не слышал, спасибо, ознакомлюсь. Да-да, мне тоже кажется, что такие модели и исследования ещё внесут масштабный вклад в наше понимание мира, рад, что есть люди, которые этим занимаются на таком уровне, целыми НИИ.
Когда я работал над обучением сетки динамике частиц, меня прямо поразило то, как некоторые известные из физики вещи как будто бы сами естественным образом вылезают из этой задачи - ну, например, касаемо лагранжиана.
Я подбирал лосс-функцию исходя чисто из желания "чтобы симуляция не бомбила и выглядела более-мне правдоподобно", и пришел к тому, что надо оптимизировать дельту энергий состояний, помноженную на дельту времени - в смысле, что на практике было бы идеально совершать максимально длинные шаги, при этом вызывающие минимальное отклонение в энергии. Ну, или если шаг фиксированный, то просто минимизировать эту величину. Величина получается в джоуль-секундах. "Где-то я это видел", подумал я) И вспомнил, что это, вообще говоря, action, который в The Principle Of Stationary Action, фундаментальнейшем принципе физики)
Добавим сюда же следующее наблюдение: в идеале надо бы шаг интегрирования сделать не общим для всех частиц, а локальным - ну то есть, вот в этой симуляции столкновения, допустим, приходится делать достаточно много под-шагов, чтобы не "бомбануло", из-за высокой энергии столкновения. Но ведь вдали от точки столкновения в течение долгого времени частицы весьма "холодные", они себя нормально ведут даже при очень маленьком количестве шагов интегрирования! Если бы удалось реализовать увеличение количества под-шагов (уменьшения шага интегрирования) в зависимости от плотности энергии... Но опять я это где-то видел - это же time dilation!)
Вообще, если уж так фантазировать, то это выглядит так, будто вселенная старается оптимизировать вычислительные ресурсы при помощи принципа стационарного действия, замедления времени и второго закона термодинамики (стараясь максимально рассеять энергию в пространстве, повышая энтропию и снижая плотность энергии, а значит, и количество необходимых вычислительных мощностей) - все ресурсы идут на вычисление всяких крутых высокоэнергетичных штук типа нейтронных звёзд и черных дыр, а остальное достается менее вычислительно-затратная областям)
Но, конечно, это запросто может быть "поиск глубинного смысла" там, где его нет. В любом случае, у меня пока даже не получилось сделать шаг локальным - симуляция взрывается при взаимодействии двух областей с разными шагом интегрирования) Возможно, с этим можно что-то сделать, но пока я этот вопрос отложил. В любом случае, это все очень интересно)

phenik
17.07.2023 17:38Смотря для какой задачи логичнее
Логичнее для тех задач, для которых имеется необходимый объем эмпирических данных, нет мат. моделей, или расчет по ним весьма затратен. Например, мы хотим предсказать динамику пламени, которую зафиксировали на видео. Для этого подаем на вход сети кадр и пытаемся предсказать следующий. После обучения она должна с некоторой точность предсказывать эту динамику для других условий. Но есть задачи для которых такой набор эмпирических данных получить затруднительно. Для той же задачи 3-х тел. Где в природе найти такую систему и долго наблюдать и фиксировать ее поведение, которое затем использовать для обучения? Желательно для разных случаев с разными параметрами? В этом случае можно использовать только вычисленные траектории. Однако в этом случае нет гарантий, что поведение реальных систем будут именно таким, т.к. обучение происходило по симуляциям, а они подвержены не только накоплению вычислительных ошибок, но ограничений исходных формальных моделей. Например, модель ньютоновская, а в реальности, в случае сильных потенциалов, тела могут испытывать взаимодействия описываемые ОТО. Или вообще неизвестных эффектов. Конечно этому подвержено и обучение на конечном наборе эмпирических данных, но в меньшей степени. Оно как раз имеет смысл для учета необычного поведения, не поддающегося формальному описанию. Вероятно, в каких-то случаях, полезно и комбинированное обучение, как по эмпирическим данным, так и симуляциям.
Но, конечно, это запросто может быть "поиск глубинного смысла" там, где его нет.
Да, конечно. В реальности никакого пламени и его динамики нет, да и частиц с примитивным законом взаимодействия также. Это приближенные модели, не важно, на уровне восприятия, или абстрактного описания. Мне, как физику по образованию занятому в психофизиологических исследованиях, трудно ассоциировать эти модели с реальностью. Скорее это отражает устройство мозга, его нейросетей, которые экономят энергию на функционирование, не только по тому что это дорогой для организма ресурс, но и опасный из-за чрезмерного выделении тепла при метаболизме. Разработчикам микропроцессор этот эффект хорошо известен, и является одной из основных проблем в их разработке. Мозг эволюционно настроен на экономию описания на всех уровнях начиная от восприятия и завершая высшими формами мышления у человека. Что там в реальности, что там во Вселенной достоверно не известно. Физики для описания поведения объектов используют разнообразные вариационные принципы, которые не могут обосновать, и они носят статус эвристических, методологических. А в нейрофизиологии управление поведением, восприятие, мышление, и др. ментальные феномены регулируются принципом свободной энергии, носящего фундаментальный характер, и могущего внести ясность в источник происхождения физических вариационных принципов. Возможно эта та причина благодаря которой подход предлагаемый Ванчуриным имеет под собой некоторые основания — не сама Вселенная является обучаемой нейросетью, а ее ментальный образ в обученных нейросетях мозга.

Ariman Автор
17.07.2023 17:38Это понятно, я скорее о том, что есть чисто практически задачи - ускорить расчет рассеивания света в облаках, например - как это сделали исследователи из RnD отдела Диснея. У них была модель, которая давала подходящие результаты, но вычисление было медленным. Они использовали ее для обучения нейросети, при помощи которой получили реалтайм расчет - он, может, и расходится с реальностью на каком-то знаке после запятой, но так как это не для фундаментальных исследований, а для реалтайм генерации реалистичных изображений, эти расхождения не так важны.
По поводу второго тезиса - ну, "вселенная как нейросеть" это, конечно, может быть чересчур, но сам подход "мы ищем модель, которая будет согласоваться с наблюдениями и при этом минимизировать вычислительные затраты", как мне кажется, может оказаться полезным.
Я имею в виду, что минимизация экшена (того, что джоуль-секудны) и замедление времени в присутствии высокой плотности энергии, вместе с возрастающей энтропией (то есть, с все возрастающим рассеиванием этой энергии всем возможным количеством способов), как будто бы одновременно являются механизмами, которые позволяют сократить вычислительные затраты.
Разумеется, я отдаю себе отчёт в том, что настоящие физические модели, которые описывают квантовые поля - это совсем не то же самое, что точечные частички в потенциале) Но принципы, которые я упомянул, мне кажется, в той или иной мере могут быть экстраполированы.

SeregaSA73
17.07.2023 17:38А энергию частицы передают только через столкновения, тепловое излучение не учитывается?

Ariman Автор
17.07.2023 17:38Ну, конечно не учитывается - это же нужно, получается, параллельно моделировать электромагнитные эффекты - совсем другая задача. Максимум, что я в этом плане делал - "подкладывал" под симулируемые частицы вторую симуляцию, распространения волн в плоскости - это не особо "физично" было, в том смысле, что я не стремился этим промоделировать какие-то реальные эффекты, скорее было просто интересно, что из этого получится (я так симулировал звук от своего парового двигателя на этих частичках) - ну вот можно в это поле энергию сливать) Будет poor man's "излучение")
Вот так это выглядит. Тут это "поле" специально только в нижней части, но вообще я его подкладывал и прямо под частицы. В моем коде частицы вызывали изменения амплитуды в этом поле, а само оно на них никак не влияло, но думаю, можно при желании закодить и так, чтобы энергия перетекала в него и обратно.

raamid
17.07.2023 17:38+2При большом количестве частиц они ведут себя как жидкость или газ. Не пробовали решать уравнения Навье-Стокса? Интересно было бы посмотреть на поведение разных математических моделей в одинаковых условиях.

Ariman Автор
17.07.2023 17:38+1Да, ведут, вон я их кипячу и дистиллирую)
Модели, которые описывают усреднённую динамику частиц я пока не использовал - собственно, это и есть одна из причин, по которым я начал этот проект - мне интересно, можно ли получить нейросеть, которая будет повторять динамику этих моделей (типа того же Навье-Стокса), но при этом выведет ее сама из данных, полученных при симуляции жидкостей на уровне частиц.

raamid
17.07.2023 17:38+1Очень интересно. По идее что-то получиться должно. Мне кажется главный вопрос жизни, вселенной и всего такого - сможет ли нейросеть стать более эффективной с точки зрения точности и вычислительной эффективности по сравнению с классической системой уравнений Навье-Стокса. На стороне классики - отсутствие лишних вычислений связанных с ненужными коэффициентами нейросети. На стороне нейросети - способность обобщать, соответственно, не нужно использовать сплошную мелку сетку.

raamid
17.07.2023 17:38+1Оказывается в последнее время исследования на тему моделирования жидкости и газа при помощи нейросетей ведутся довольно активно.
Вот короткое видео, в котором показано что-то вроде MVP. Есть ссылки на статьи, проект на Гитхаб
https://www.youtube.com/watch?v=ISp-hq6AH3Q
Отличная презентация того как устроено моделирование жидкости при помощи Навье-Стокса и нейросетей.
https://www.youtube.com/watch?v=IXMSOSEj14Q
На самом деле, информации очень много, хотелось бы привести больше ссылок, но лучше просто погуглить "neural network navier stokes".
Надеюсь, будет полезно.

AcckiyGerman
17.07.2023 17:38Есть такая игра
https://noitagame.com/
Автор очень хорошо реализовал физику частиц в 2D. Вам будет интересно взглянуть и может быть почитать devlog.
Ariman Автор
17.07.2023 17:38+2Я знаю и люблю эту игру. Но физика частиц там очень специфическая, в силу ограничений, накладываемых самой задачей - им нужна очень быстрая реалтайм модель, в которой не так важна физическая достоверность и разнообразие взаимодействий)
Поэтому тамошние частички очень упрощённо взаимодействуют друг с другом и не образуют макро-структур. Вы не увидите в Нойте результатов столкновений типа того, что в заголовке поста, не будет слипающихся друг с другом "осколков", не будет настоящего кипения и т.п. Это я не к тому, что "а-ха-ха, смотрите, а у меня лучше", а к тому, что это разные модели для разных задач.
Если у меня получится ускорить вычисления при помощи нейросети, попробую собрать на этом какой-нибудь интерактив)
Кстати, то количество частиц, что в примере impact, в целом, более-менее реалтаймово тянется. ФПС на 20 вместо 50, но всё-таки. Но все красивые штуки, в основном, требуют большую плотность энергии, а значит - увеличение количества под-шагов интегрирования. Дистилляция, например, тоже даёт примерно 30 ФПС, но она при этом в 10 раз медленнее идёт, чем в гифке и на видео - в игре это не особо прикольно было бы, ждать 10 минут, пока у тебя зелье сварится.

xpbim3_xpbim3
17.07.2023 17:38Хэй! оч круто!
Делал такое 12 лет назад на с+куда+опенгл на дряхлой 8400GS... оч нравилось видеть результат симуляции.
Также делал на дипломе молекулярную динамику разделительной центрифуги для двухкомпонентной смеси и даже наблюдался коэффициент разделения, несмотря на скромное количество частиц.
Вот даже историческое демо осталось: https://youtu.be/QEkC1k0gdnI

HlebyShek
17.07.2023 17:38Красивый проект.
А вы пробовали задавать расстояние, в котором частицы взаимодействуют, в зависимости от силы взаимодействия. То есть отсекать все, сила взаимодействия с которыми меньше epsilon.
Ariman Автор
17.07.2023 17:38А зачем? Чтобы узнать силу взаимодействия и увидеть, что она меньше, чем эпсилон, надо сначала ее посчитать, то есть посчитать взаимодействие со всеми частицами из окружения, что сводит на нет смысл такой "оптимизации".
Другое дело, что я сходу не считаю взаимодействия на расстоянии больше некоторого предельного радиуса - это получается само собой за счёт того, что все взаимодействия тут локальные, частица взаимодействует только со своим непосредственным окружением как раз в этом предельном радиусе. Это автоматически ведёт к тому, что она не взаимодействует с частицами на расстояниях, на которых сила пренебрежимо мала.

zumrus
17.07.2023 17:38Очень красивые симуляции. За САЕ и МВК отдельный респект: очень люблю вторую часть Гоблинов, и эта любовь даже передалась моим детям.
По сути: не смотрели в сторону квантовомеханических симуляций в потенциале ЛД? Это сейчас хот-топик в экспериментальной атомной физике и ультрахолодной химии. Там минимум этого потенциала формирует резонанс Фешбаха, которым управляют с помощью небольшого магнитного поля. См, например, здесь
https://nplus1.ru/material/2023/02/08/supercool-four
и далее по ссылкам
zumrus
17.07.2023 17:38Ну и в целом в квантовой физике дефицит наглядных представлений. Оно и понятно: волновая функция - это функция трех координат, поэтому даже типичные атомные орбитали выглядят на картинках учебников условно и не совсем так, как их стоило бы воспринимать на самом деле.
Я обычно своим студентам привожу в пример игру Quantum Moves, в которую можно поиграть в браузере. Эта игра предлагает решить проблему перемещения атома оптическим пинцетом по нужной траектории, "не расплескав" его волновую функцию. Там, конечно, тоже двумерия, но во всяком случае оно дает студентам интуитивное представление о квантовом поведении объектов с помощью численного решения динамического уравнения Шрёдингера.
Ariman Автор
17.07.2023 17:38Если я правильно помню, то волновая функция еще и растет размерностью вместе с количеством частиц, то есть если одна частица может двигаться в трех измерениях, ее волновая функция будет трехмерная, а если таких частиц две - то уже в шести)
В смысле, пространство-то и остается трехмерным, но именно изменения в конфигурации волновой функции путешествуют уже в их совместных шести.
Нет, в сторону квантовых симуляций я пока не смотрел. Это тоже, конечно, интересно) Но я все-таки хотел бы сначала попробовать ускорить расчеты в 2д при помощи нейросетки. Не знаю, получится или нет, я пока только в самом начале исследований.
zumrus
17.07.2023 17:38Все верно) это мы ещё спин не учитываем)
Очень интересно, что у вас выйдет! Если нейросети смогут предсказывать исходы физических процессов быстрее, чем прямой расчёт, это может быть революцией. Я думаю о том, как это сможет ускорить работу физических движков, чтобы запускать реалистичную графику на слабых компьютерах

phenik
17.07.2023 17:38Если нейросети смогут предсказывать исходы физических процессов быстрее, чем прямой расчёт, это может быть революцией.
Есть уже довольно старая работа по предсказанию ВФ молекулярной электронной структуры материалов, и соответственно их свойств, в квантовой химии. Ценна также списком ссылок на нее.

maxlilt
17.07.2023 17:38+1Визуализация для уроков физики хороша. Желаю вам успешного движения глубже в квантовый мир!

Vsevo10d
17.07.2023 17:38+4Вы баффнули Хабр тортом на несколько месяцев.
Хочу сразу разъяснить читателям. В реальной жизни межатомные взаимодействия описываются именно такими кривыми, как приведенная в статье Леннарда-Джонса или потенциал Морзе (электростатические взаимодействия для атомов в составе одной молекулы).
Атомы можно ОЧЕНЬ ГРУБО представить в виде отталкивающихся друг от друга магнитов, помещенных в липкие слаймы. Магниты - это компактные ядра (которые отталкиваются друг от друга в реальности не из-за магнитных взаимодействий, это ради наглядности!), а слаймы вокруг - электронные облака (которые слипаются - аналог спаривания электронов с образованием ковалентной химической связи).
Так вот, если вы возьмете две такие штуки, и будете вжимать друг в друга, они будут яростно сопротивляться - чем ближе, тем сильнее отталкиваются магниты, поэтому потенциал слева на графике идет в бесконечность. Потом, если отпустить их, система придет в равновесие: отталкивание магнитных сердцевин уравновесится тягучестью слаймовых оболочек, будет два слипшихся шарика, потенциальная энергия этой системы придет к минимуму (та самая потенциальная яма). А если растащите еще дальше, то слаймы будут сопротивляться, пока липучести хватает, затем они оторвутся - взаимодействие прекратится вовсе. Поэтому справа график приближается, а затем становится равен нулю в зависимости от расстояния между объектами.
Еще раз: у реальных атомов между ядрами будут не магнитные, а кулоновские и квантовые силы отталкивания, а на больших расстояниях их вместе удерживают ковалентные, электростатические ионные, Ван-дер-Ваальсовы силы взаимодействия. Но надеюсь, аналогия "отталкивающе-липких шариков" получилась наглядной.
Это насчет межАТОМНЫХ взаимодействий. С межМолекулярными чуть по-другому: если атомы в молекуле стабильны, существует только отталкивание. К нестабильным (готовым образовать химическую связь) атомам могут присоединяться другие, начиная с определенных энергий столкновения. Это и продемонстрировано автором в его экзотермической реакции.
Осталось ответить на главный вопрос.
Зачем все это?
Будучи студентом химико-технологического вуза в конце нулевых, я бы поклонился вам в ноги за такие визуализации. И вообще, для популяризации и наглядности я бы очень советовал вам (ну или кто еще этот код подхватит) продолжать.
Куда можно продолжать?
физико-химические процессы: симуляция идеального газа, термодинамических изопроцессов, диффузии, адсорбции;
химические процессы: кинетика реакций 0, 1, 2 порядка, радикальные цепные процессы;
технологические процессы: реология твердых частиц, процессы в псевдоожиженном слое, осмос, ректификация;
Даже в упрощенном виде, для демонстрации, а не реальных расчетов, такие симуляции ОЧЕНЬ полезны.

f965
17.07.2023 17:38В радикальных цепных процессах было бы интересно посмотреть на формированиие ударной волны

Ariman Автор
17.07.2023 17:38Спасибо на добром слове) У меня на этот год намечены несколько проектов, если никакой очередной пиздец не наступит, попробую их довести до значимых майлстоунов. Один проект прямо сильно на базе его кода, другой - скажем так, на опыте, который я получил из реализации симулятора, с некоторым заимствованием кода из него, и третий - это вот исследования, связанные с обучением нейросети этой динамике.

stanislavskijvlad
17.07.2023 17:38+2Вот бы автор статьи, Onigiri и Техношаман52 объединили усилия и создали супер клеточный автомат с эволюцией, деревьями, светом, ресурсами и агентами.

AndrewChe
17.07.2023 17:38С какой скоростью идут расчеты и при каком количестве частиц? Есть планы добавить третье измерение? Очевидно, что вычисления идут в кернелах, но все же питон не дает оверхеда?

Ariman Автор
17.07.2023 17:38+1Оверхед от питона очень незначительный, большую часть времени идут расчеты сил. На втором месте рендер, но он дергается намного реже.
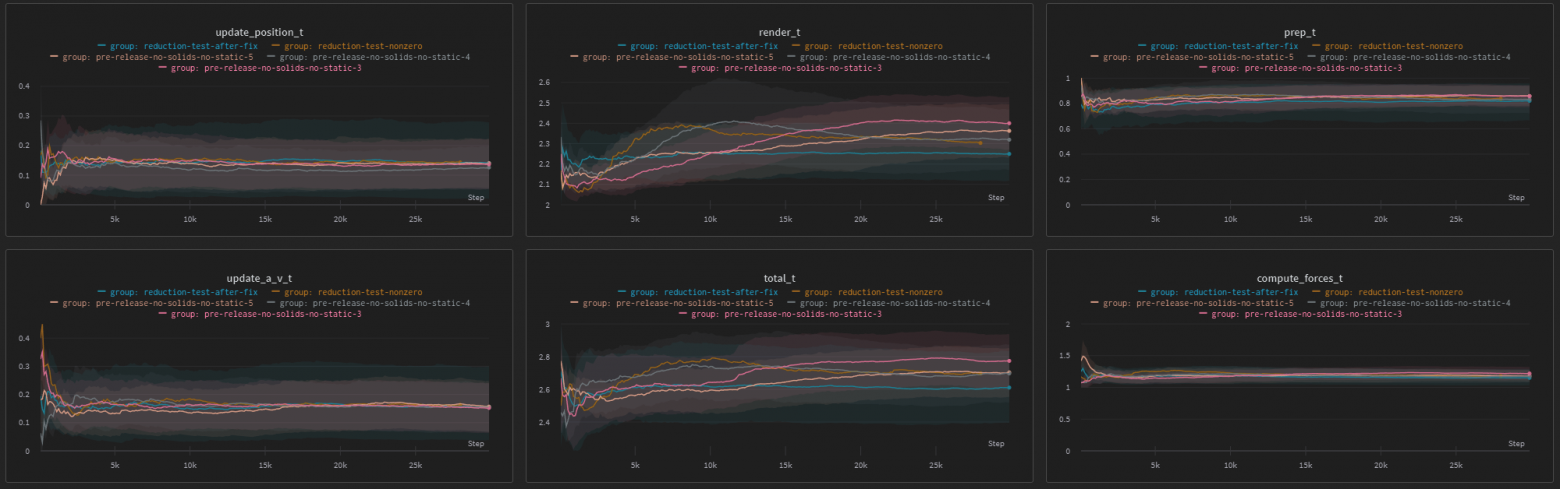
Примерно так это выглядит)
Ну вот пример из заголовка, с достаточно высокоэнергетическим столкновением при 10 под-шагах выдает у меня около 50 FPS, реалтайм. При ~30к частиц. У моей подруги на 2060 дает 60 FPS на тех же настройках. Все зависит от количества под-шагов, а оно зависит от предельной энергии, которую может выдержать симуляция, не развалившись) В этом случае 10 хватает, чтобы не бомбануло.
В более затратных, типа дистилляции, конечно, либо сам процесс будет идти медленно - у меня тоже примерно 40 FPS выдает, но сама дистилляция длится 10 минут (в видео ускорено в 10 раз) - либо надо повышать энергию частиц вместе с количеством под-шагов.
65к частиц примера vortex, где они с большими энергиями крутятся, у меня идет на 15 фпс примерно, на ноуте.
Нет, 3д я пока не планирую, там нужно много чего менять будет прямо в самом сердце алгоритма, в расчете сил. Сейчас он базируется на 2д hash-grid (или, как я это зову, "поле индексов"), и этот код я достаточно долго оптимизировал - собственно, эти графики - это как раз и есть процесс оптимизации, я пробовал разные штуки и замерял скорость. В 3д нужно уже что-то другое придумывать и снова оптимизировать.
Я, скорее, вместо 3д буду пытаться 2д ускорить, очень уж хочу дистилляцию быструю и в реалтайме.

yesworld
17.07.2023 17:38+2Очень крутая статья, спасибо! Если в школе по физики была бы подобная визуализация, я бы реже прогуливал уроки. :)
Творческих успехов, буду ждать более подробнее про то, как реализованы хотя бы несколько примеров!

Celahir
17.07.2023 17:38Я правильно понимаю, что вы пишете аналог симулятора LAMMPS, только на Python? Чем не устраивает этот симулятор на C++? Он вроде под открытой лицензией и часто используется в научных исследованиях для симуляции частиц и химических реакций.

Ariman Автор
17.07.2023 17:38
Ну, я на это уже отвечал. "Таких винтовок много, но эта - моя")
Хотя на самом деле - не то чтобы много. Даже если опустить тот момент, что мне захотелось разработать эту штуку самому, она еще и на других технологиях. Этот симулятор полностью на питоне, что позволяет его очень легко стыковать с пайплайном машинного обучения. Я его сделал для не для исследований химических реакций, а для исследований в области машинного обучения, прежде всего.
И мне копаться в своем питоновском коде (зная каждую его строку, каждый компромисс, каждую оптимизацию) куда проще, чем прикручивать к питоновскому пайплайну с пайторчем эту махину на C++ и перекомпилять ее каждый раз, когда мне потребуется там что-то отрезать или прикрутить)

Ariman Автор
17.07.2023 17:38Случайно промахнулся и отклонил чей-то коммент, не успел запомнить автора. Автор, прошу прощения, напиши еще раз) Там было про кулоновский потенциал и про то, с ним не получится считать воздействия только ближайшего окружения. Почему, кстати? Он же тоже падает до нуля с расстоянием.
И, кстати, почему некоторые комменты не сразу постятся, а ожидают от меня подтверждения? Это при низкой карме?
azTotMD
17.07.2023 17:38Почему, кстати? Он же тоже падает до нуля с расстоянием.
Падает не так быстро, как хотелось бы. Поэтому накапливаются слишком большие ошибки, если поступать с ним как с короткодействующими потенциалами. Обычно электростатику считают методом Эвальда (PME, Particle mesh Ewald), у меня есть небольшая статья про это. Но в одной из работ показано, что можно вместо Эвальда использовать хитрый короткодействующий потенциал. Если надо, найду эту работу и формулу.
ПС, начальный коммент не мой, не знаю, что там было

Ariman Автор
17.07.2023 17:38А, понятно. Я что-то подумал, что речь о кулоновском барьере, о взаимодействии на уровне нуклонов уже, не сразу понял, причем тут он.

nk11k
17.07.2023 17:38Лет 10 назад (ВолГУ, 2013) писал дипломную по ускорению алгоритма Барнс-Хата на видеокартах NVIDIA. Изначально был старый код на Фортране и входные данные для него. На курсовых 2010-2012 переписывал одномерную и двумерную версию с использованием PGI CUDA Fortran Compiler, а в дипломной попытался в 3D, но в одиночку не осилил, и нашёл в итоге treecode/bonsai на C++/CUDA, который смог скомпилить под винду и адаптировать входные параметры в нужный формат. Далее всё это запускалось на рабочих станциях с Tesla C2050 под виндой. И визуализатор там тоже был, выглядит как-то так: https://www.youtube.com/watch?v=aPgzo9Mvk6o
Немного не по теме, т.к. BH в основном используется для гравитационных симуляций, но наверное тоже можно использовать для обычных симуляций с частицами?

Ariman Автор
17.07.2023 17:38Да, но тут ситуация немного другая - за пределами нескольких
потенциал почти нулевой, в основном тут важно именно действие соседних частиц. BH, если я правильно понимаю, скорее для случая, когда есть силы, тянущиеся на огромные расстояния - слипающиеся под гравитацией частички для других, удаленных от них, частиц, выглядят как одна большая гравитирующая масса, поэтому ее нельзя просто так отбросить.

nk11k
17.07.2023 17:38Да, наверное оптимизировать расчёт разбивкой на динамическую сетку здесь не получится.
Хотя, если у нас в симуляции 10,000 частиц, то сложность алгоритма будет O(N*K), где K — максимальное количество соседних частиц? По-идее сейчас количество CUDA-ядер и shared memory сильно больше, чем в 2013, и если попробовать разбить симуляцию на квадраты/кубы (2D/3D) одинакового размера, то каждое ядро сможет параллельно обсчитывать десятки тысяч взаимодействий на цикл. Только вопрос будет в граничных условиях, можно ли обойтись без копирования частиц из соседних блоков памяти.
Поправьте, если не так.
Ariman Автор
17.07.2023 17:38Так он и сейчас оптимизирован, потому что обсчитывается только ближайшее окружение. Что-то типа BH вводить, я так понимаю, имеет смысл, если что-то за пределами этого окружения вносит большой вклад, который нельзя отбросить - не для скорости, а для точности. Типа того, что выше сказали про кулоновское притяжение/отталкивание.
В том коде, который сейчас, как мне кажется, надо смотреть в сторону какой-то хитрой магии с количеством шагов интегрирования. Не дает мне покоя тот факт, что при том же столкновении большинство частиц не требует такого большого количества под-шагов (маленького шага интегрирования), потому что до них далеко не сразу докатывается волна, да и после того, как она схлынет, они тоже вполне могут быть просчитаны с очень небольшим количеством под-шагов. Много шагов интегрирования нужно только там, где высокая плотность энергии, а она совсем не одинаковая в пространстве, да еще и постоянно падает (солдат спит - энтропия растет!). Но пока у меня не получилось интегрировать с разным шагом, симуляция взрывается) Это как раз то, на что идет большая часть вычислительных ресурсов, и частичкам, которые движутся совместно (даже с большой общей скоростью) не особо нужны эти промежуточные точки, но так как шаг общий для всех, на это тратится куча ресурсов.

azTotMD
17.07.2023 17:38попробовать разбить симуляцию на квадраты/кубы (2D/3D) одинакового размера
так и делают, это называется cell list
Только вопрос будет в граничных условиях, можно ли обойтись без копирования частиц из соседних блоков памяти.
Все приходится держать в global memory

alexanicus
17.07.2023 17:38Интересная работа. Сам много лет, как хобби делаю подобные симуляторы время от времени. Но в этом году делаю уже ЭМ взаимодействие заряженных частиц с учетом ТО методом учета потенциалов Лиенара-Вихерта и как следствие в 3d.
Проблеме интегрирования (и взрыва) посвятил много вечеров, в конечном итоге пришел к формуле, которая конечно усложняет вычисление одной пары, но значительно уменьшает ошибку.
Суть ее в том, что силу между точками интегрирования, нужно проинтегрировать и получить среднее.
Скажем для кулоновской силы F = k / (R[t] * R[t+1]), действующая сила будет зависеть от будущего положения :) но у этого парадокса таки есть решение, которым поделюсь если найду силы и вдохновение опубликоваться на хабре.
В вашем случае потенциалов "6-12" даже проще, вам нужно учесть, что суммы энергий не изменились до и после просчета для каждой пары: Vi+Ui +Vj+Uj = const . Кстати такая поправка уменьшает проблему порядка расчета и проблему float32 ошибки. Кстати эти размышления приводят к необходимости введения квантования энергии))
Для контроля ошибки можно применять такие показатели:% отклонения энергии всей системы
средне квадратичное отклонение между расчетами с разными шагами интегрирования (например, 1 секунда за 10 шагов, против 1 секунда за 1000 шагов) Предлагаю создать чат группу Telegram - любителей симуляции частиц))

Ariman Автор
17.07.2023 17:38нужно учесть, что суммы энергий не изменились до и после просчета для каждой пары: Vi+Ui +Vj+Uj = const
Но это не похоже на правду. Или я не так понял это предложение. Если во взаимодействии участвуют несколько частиц, то не изменилась сумма энергий их всех, а не каждой пары в отдельности. А в этом случае не очень понимаю, как мне поможет то, что я знаю локальную сумму энергий, распределиться по частцам-то она могла как угодно. Можно попробовать собирать эту локальную плотность энергии и при ее помощи попытаться локально же масштабировать скорости, но это надо учитывать все частицы, которые были во взаимодействии в t0 и t1 (включая те, что влетели в радиус взаимодействия и вылетели оттуда).
Суть ее в том, что силу между точками интегрирования, нужно проинтегрировать и получить среднее.
Ну так это вычислительно примерно то же самое, что и интегратор более высокого порядка получается же? Хотелось бы не просто сложность вычислений повысить ради точности, а увеличить скорость расчетов.
Вот про метрики для ошибки - совершенно согласен, сам к таким же пришел. Более того, если предположить, что делаем динамический шаг, и нам нужно, чтобы система совершила шаг, максимальный по времени и минимальный по отклонению, получается, что нужно оптимизировать dE*dt - что внезапно совпадает с экшеном (тем, что джоуль-секудны) из принципа стационарного действия!
На мой взгляд, больше всего лишних вычислительных ресурсов тратится на под-шаги интегрирования там, где этого не требуется - я выше про это писал, в примере со столкновением, например, большая часть частиц могла бы быть просчитана с 1-2 шагами на кадр, только в точке удара (и на гребне распространяющейся волны) требуется больше. Поэтому нужно бы что-то вроде time dilation, замедления времени в присутствии большой плотности энергии, сделать количество под-шагов локальным и зависящим от локальной плотности энергии, чем больше - тем больше шагов, тем сильнее "замедляется время". Но на практике у меня пока не получилось это реализовать, взрывается)




azTotMD
Это всё 2Д? Трехмерное не поддерживается?
Каким алгоритмом перебираются пары частиц? Cell List, Verlet List ? Можно глянуть особенности реализации? Это ваша часть или библиотечная?
Ariman Автор
Да, это 2д симулятор. Весь код мой, потому что он, в основном - кернелы для CUDA, написанные на Питоне, которые Numb'ой компилятся на лету под GPU - мои вкусы весьма специфичны) Весь остальной код на Питоне - это обертки для вызовов CUDA Kernel'ов и всякая вспомогательная фигня, склеивающая эти вызовы в итоговый продукт.
Я использую что-то вроде hash grid, чтобы обеспечить локальность взаимодействий - в 2д массив записываю индексы частиц в соответствии с их координатами (я это зову полем индексов), а дальше в дело вступает параллельность GPU (ну, точнее, там все расчеты на GPU проводятся, просто особенно важно это именно в вычислении сил, это самая вычислительно-затратная часть, не считая рендера).
Я беру каждую частичку и стартую NxN тредов для нее, где N - это округленный до ближайшего инта максимальный радиус взаимодействия. Его можно поменять, но по дефолту он равен 5, то есть по 25 GPUшных тредов на частицу. Каждый из них смотрит свою ячейку поля индексов, вычисляет силы от частиц из этой точки и плюсует их в переменную, хранящую силы, действующие на частицы.
Посмотреть это можно в репозитории, в начале поста ссылка. Вычисление сил находятся в simba_ps/physics_kernels.py : compute_forces
azTotMD
свою и соседние?
Ariman Автор
Нет, только свою. На каждую частицу порождается NxN тредов, смотрящих ее окружение.
azTotMD
тогда получается есть шанс, что не все частицы, которые рядом, провзаимодействуют? если наша частица близко к границе ячейки?
Ariman Автор
Нет, почему же? Представьте поле из 5х5 клеточек, центрированное на каждой из частиц. В смысле, к каждой частице как бы привяжем такой квадратик из 5х5 клеток, поместив частицу, для которой происходит расчет, в центральную. Круг с радиусом, равным максимальному радиусу, на котором частицы еще взаимодействуют, оказывается вписан в этот квадрат.
azTotMD
Представил. Как перебрать все частицы внутри квадрата? Как получить список таких частиц?
Ariman Автор
Список и не надо, каждая клетка квадрата - это отдельный поток. Все, что ему нужно сделать - это обратиться к "полю индексов" в соответствии со своей позицией, и посмотреть, есть ли в этом месте частица. Если есть - посчитать, какое от нее будет воздействие на ту, к которой он принадлежит, и добавить результат к переменной-аккумулятору сил. Это же на видюхе все считается, каждая клетка каждого квадратика обсчитывается отдельным тредом.
azTotMD
это всё понятно, вопрос вот где:
Можно здесь подробнее, как это работает? Что такое "поле индексов"?
одна? может быть в клетке больше одной частицы?
Ariman Автор
Ну я же выше писал... И в самой статье. В зарубежной литературе это зовут hash grid.
Да, там может быть несколько частиц, считайте, что на каждой клеточке стоит колонка, в которой может вообще не быть частиц, а может быть одна или несколько, тред этой клеточки по ним последовательно проходит, просто пока не встретит невалидный индекс.
Так как я задаю около 1.0 (в редких случаях, типа симуляции химии с молекулами может быть что-то типа 0.7), система естественным образом стремиться частицы раскидать так, чтоб в клеточке больше одной не было. Они могут туда влететь на короткое время, за счет своей энергии, но ненадолго, и редко когда их там больше штук 3-5.
я задаю около 1.0 (в редких случаях, типа симуляции химии с молекулами может быть что-то типа 0.7), система естественным образом стремиться частицы раскидать так, чтоб в клеточке больше одной не было. Они могут туда влететь на короткое время, за счет своей энергии, но ненадолго, и редко когда их там больше штук 3-5.
Да, если по каким-то причинам в симуляции бешеная плотность частиц, то этот "столбик" может заполниться, наверное - для этого у меня там даже есть print, который об этом скажет, но до сих пор такого не было, потому что это все раньше отвалится из-за недостаточного шага интегрирования, либо вовсе до этого не дойдет, если шаг будет достаточным (тогда частицы просто успеют провзаимодействовать раньше и разлететься).
Я почему это все зову по-своему - во-первых, я это дело писал сам, в смысле, чисто решал эту задачу, как мне казалось правильно и эффективно, и только потом узнал, что у этого есть какое-то свое название, а во-вторых - я же это все в машинном обучении использовал, а там все эти индексы пропадают, сетка видит только окружение частиц, как картинку. Для нее это - как будто обсчет небольшого кусочка поля, она выполняет локальный расчет на своем квадратике. Поэтому, по аналогии и "поле индексов" - такое фейковое поле, которое обеспечивает локальность расчетов, когда их производит не сетка, а написанный ручками код.
azTotMD
Спасибо!
Un_ka
Жаль, на google Colab запустить не получится.
А ведь такими методами, если всё-таки смоделировать в объемном случае (он нужен в виду природы турбулентности) горение топлив с учётом 20..50 компонентов и верифицировать подобную модель, то с помощью её уже можно будет обучать сети совместимые с RANS моделями турбулентности. Вдруг получим модель на основе сети с точностью и быстродействием превосходящим существующие?
Ariman Автор
Ну, one step at a time. Как я упоминал в статье, практическая сторона этого вопроса мне тоже очень интересна, поэтому я, собственно, и начал эксперименты - но не стал сразу замахиваться на сверхсложные модели, нужно сначала отработать технологию в 2д) А так - да, очень может быть, это одно из направлений, в котором сетки активно применяют. Я точно знаю, что Дисней разрабатывал технологию, ускоряющую расчет рассеивания света в облаках за счет обученной нейросетки - там как раз такой же принцип - учим на медленной симуляции, потом используем быструю сетку.
Но такое применение довольно очевидно любому, кто хоть чуть-чуть сталкивался с нейросетями. Проблемы начинаются именно в реализации, там хренова тонна вещей, которые можно реализовать по-разному, и, вообще говоря, никто не скажет заранее, какой из вариантов лучше, какой хуже, а какой вообще не заработает. Я вот совсем не сразу подобрал подходящий энкодинг, архитектуру, да и вообще задолбался этот пайплайн строить и отлаживать) Но все-таки сетка обучилась, хотя пока, конечно, медленнее чем мой, довольно оптимизированный, код расчета. Сейчас вот отдохну немного от релиза, и продолжу эксперименты. Мне очень хочется реалтайм дистилляцию получить) Хочу алхимию)
А почему, кстати, не запустить в коллабе? Я этот код удаленно на своей линуксовой машине стартовал вообще без проблем. Только рендер надо отрубить - ну, точнее, не надо врубать, он отдельно от симулятора. И мне кажется должно стартануть.