По мере развития технологий в мире появляется все больше различных технологических алгоритмов. Часть из названы в честь ученых, имеющих отношение к их разработке, другая часть имеет простые (или не очень простые) «сухие» названия или же забавные наименования, например, коктейльная сортировка (Cocktail shaker sort), в русском языке называемая просто — «сортировка перемешиванием». Сегодня поговорим про алгоритмы, названные в честь различных представителей животного мира.

Довольно долгое время ученые «подсматривали» за поведением животных и использовали полученные знания для решения технологических проблем. В основном звериные алгоритмы представлены в роевом интеллекте. Это самоорганизующиеся системы, состоящие из множества особей. Животные объединяются в рой, стаи и стада для решения общих задач, главным образом — поиска пищи.

Упомянутые в статье алгоритмы как раз относятся к роевому интеллекту. Как правило, чаще всего они применяются для решения проблем оптимизации, но нередко их используют в логистике, сортировке и других задачах.

Оптимизация методом сальп

Сальпы — свободно плавающие морские существа, похожие на прозрачные бочки. При поиске пищи они нередко собираются в причудливые цепочки или спирали из нескольких особей. Первый сальп в цепочке — лидер и ведущий, при этом любой другой сальп может решить проблему поиска пищи. Проплывая по участку, они фильтруют воду и добывают таким образом себе еду.

Ориентируясь на поведение сальп, исследователи разработали алгоритм оптимизации. В начале он случайным образом размещает в пространстве множество условных сальп, после чего для каждой из них определяется значение целевой функции. Сальпа с наилучшим значением вместе с ее координатой будет представлять собой «источник еды», за которым охотится группа сальп со своими ведущими и ведомыми. Когда группа находит «источник еды», его положение обновляется.

Алгоритм подходит для оптимизации задачи с неизвестным пространством поиска благодаря простоте применения и реализации, наличию только одного параметра для настройки и сохранения наилучшего текущего значения, которое не будет потеряно даже в случае вырождения популяции. Кроме того, сальпы в цепочке постепенно смещаются в сторону ведущей сальпы, что предотвращает застревание в точке локального оптимума.

Вот несколько примеров применения этого алгоритма в реальной жизни:

1. Оптимизация энергопотребления в сетях передачи данных, например, в беспроводных сенсорных сетях или сетях интернета вещей. Он может помочь в нахождении оптимальной конфигурации сети, минимизирующей потребление энергии при сохранении надежности связи;

2. Поиск оптимального распределения ресурсов в облачных вычислениях. Алгоритм может помочь в определении наилучшего распределения вычислительных задач между серверами, чтобы минимизировать время выполнения и снизить нагрузку на систему;

3. Распределение задач в мультиагентных системах, где несколько агентов должны совместно выполнять задачи. Алгоритм сальп может быть использован для оптимизации распределения этих задач между агентами. Он может помочь в достижении баланса нагрузки и улучшении общей производительности системы.

4. Оптимизация параметров при проектировании инженерных систем, например, при проектировании аэродинамической формы автомобиля, в определении оптимальных значений параметров, таких как форма кузова или расположение аэродинамических элементов, для достижения минимального сопротивления воздуха и повышения эффективности топлива.

Алгоритм стаи криля

Криль — группа животных, к которой относятся мелкие морские рачки длиной до 65 мм. Большинство представителей этой группы собираются в огромные стаи и вылавливают микроскопические одноклеточные растения (фитопланктон), представляющие собой основу рациона криля.

Непрерывный алгоритм стаи криля (метод непрерывной оптимизации) имитирует перемещение криля при поиске пищи с учетом взаимосвязанных факторов: наличие хищника, заставляющего криль держаться в стае, поиск пищи и случайное блуждание криля. Хищник регулирует плотность стаи и направление движения. Движение одного конкретного криля в стае также зависит от движения его соседей, ведущего криля в частности и поискового поведения стаи. Наилучшее значение каждого криля представляет собой комбинацию расстояния от еды до самой плотной точки стаи.

Поведение криля имитируется для поиска оптимального решения вопросов оптимизации. Все полученные допустимые значения расстояния до еды представляют собой потенциальное решение. Наилучший криль в стае потенциально дает наилучшее решение проблемы. 

Вот несколько примеров его применения в реальной жизни:

1. Распределение ресурсов в сетях электроснабжения, например, он может помочь в определении оптимального распределения нагрузки между генерирующими и потребляющими узлами, чтобы достичь баланса между производством и потреблением энергии.

2. Маршрутизация в компьютерных сетях. Алгоритм может помочь в нахождении наилучших маршрутов передачи данных между узлами сети, учитывая такие факторы, как пропускная способность и задержка, с целью повышения производительности сети и снижения потерь.

3. Оптимизация процессов производства в промышленности. Например, алгоритм может помочь в нахождении оптимальных параметров производства, таких как скорость и настройки оборудования, чтобы максимизировать производительность и снизить издержки.

4. Оптимизация распределения ресурсов в логистических системах, помощь в определении адекватного маршрута доставки грузов или распределения ресурсов между складами и транспортными средствами, чтобы сократить время и затраты на доставку.

Кузнечик

Grasshopper Optimization Algorithm (GOA) — алгоритм оптимизации, названный в честь всем известного насекомого. Кузнечики живут практически на всех континентах и нередко представляют угрозу для других существ из-за особенностей своего поведения при поиске пищи. Кузнечики передвигаются плотным роем, иногда достигающим огромных размеров, сметающим все на своем пути.

Алгоритм GOA имитирует не только процесс поиска пищи и манеру передвижения роя кузнечиков, но и базовые процессы «размножения». Учитываются факторы расположения каждого отдельного кузнечика, дальность от другой особи, скорость ветра, влияющая на передвижение, и даже сила тяжести. Условно процесс передвижения делится на два этапа: исследование и эксплуатация. На этапе исследования рой ищет источники пищи, а после определяет лучшие решения среди всех (лучшие источники пищи).

Вот несколько примеров его применения в реальной жизни:

1. Оптимизация маршрутного планирования в транспортных системах, например, для определения наилучших маршрутов доставки грузов или пассажирских перевозок. GOA помогает учесть различные факторы, такие как время, расстояние, пропускная способность дорог и другие ограничения, чтобы найти наилучшие маршруты.

2. Кластеризация данных, когда требуется группировать объекты по схожести. Например, в области машинного обучения и анализа данных. GOA может помочь в оптимальном разделении набора данных на кластеры, учитывая различные характеристики исходных данных.

3. В задачах машинного обучения GOA может быть применен для оптимизации параметров моделей. Например, алгоритм может использоваться для настройки параметров нейронных сетей или генетических алгоритмов, чтобы достичь наилучшей производительности модели на конкретной задаче.

4. Оптимизация планирования ресурсов в производственных системах, например, помощь в оптимальном распределении рабочих мест, оборудования и материалов на производственных линиях для повышения эффективности производства и минимизации затрат.

Муравьиный алгоритм

При создании муравьиного алгоритма ученые ориентировались на поведение муравьев при поиске оптимального пути от колонии до источника пищи. Муравьи случайно разбредаются по территории. Когда еда находится, муравей прокладывает путь от нее до муравейника при помощи феромонов. Феромоны быстро испаряются, поэтому, чтобы не потерять дорогу к пище, со временем колония муравьев корректирует путь и находит самую короткую дорогу.

В случае с алгоритмом роль муравьев играют узлы. Условные муравьи запоминают свой путь по этим узлам, и с каждым новым шагом пополняется не только список возможных узлов как возможных вариантов троп, но и список «запретных» узлов. При выборе узла муравей ориентируется на длину ребра и опыт прохождения по ним у других муравьев. Следы условных феромонов со временем испаряются с наиболее непривлекательных узлов и ребер, поскольку перед каждой итерацией алгоритма список «запретных» узлов опустошается. Таким образом муравьями прокладывается самый короткий и оптимальный путь по узлам.

Чаще всего муравьиные алгоритмы используются для решения логистических задач, например, решения задачи коммивояжера, заключающейся в прокладывании наиболее подходящего маршрута. Но они также используются при решении задачи о назначениях, раскраске графов, маршрутизации и так далее.

Вот несколько примеров применения этого алгоритма в реальной жизни:

1. Оптимизация маршрутизации в компьютерных, телекоммуникационных сетях или сетях передачи данных. Алгоритм помогает в поиске оптимального пути для передачи информации, учитывая различные факторы, такие как пропускная способность, задержка и стоимость связи.

2. Решение задачи коммивояжера — задачи нахождения кратчайшего пути, проходящего через все заданные города и возвращающегося в исходный город. Он может быть применен в логистике, транспортировке грузов, планировании маршрутов доставки и других задачах, где требуется оптимальное планирование пути.

3. Решение задачи кластеризации данных, где требуется группировка схожих объектов. Алгоритм может помочь в определении оптимальных кластеров, основываясь на сходстве исходных параметров, и помочь в их анализе и принятии решений.

4. Оптимизация расписания, например, в задачах планирования занятий в учебных заведениях или распределения ресурсов в производственных системах, в нахождении оптимального расписания, учитывая различные ограничения и предпочтения.

5. Оптимизация маршрутов транспорта в логистических системах. Алгоритм может помочь в нахождении оптимальных маршрутов доставки грузов или планирования маршрутов транспортных средств для снижения времени и затрат на доставку.

Алгоритм роя пчел

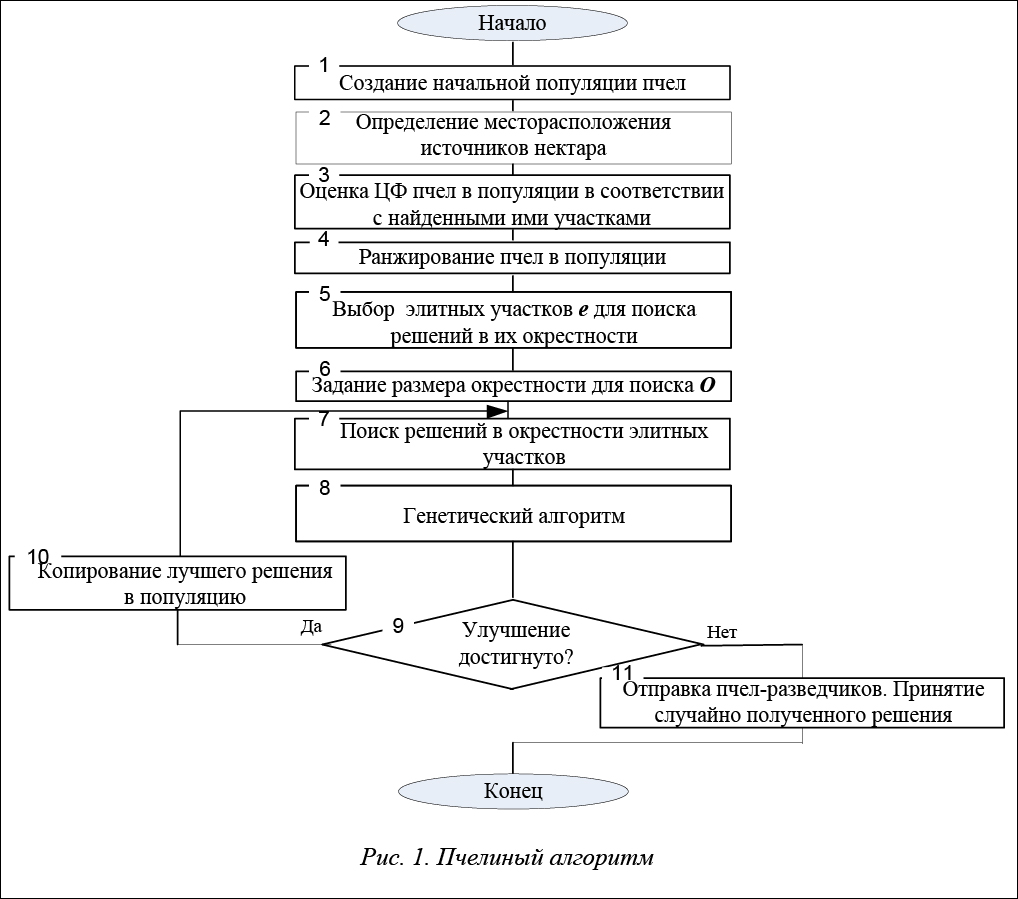
Алгоритм роя пчел, он же метод роя пчел, он же artificial bee colony optimization (ABC) — еще один алгоритм из категории роевого интеллекта, описывающий поведение самоорганизующейся системы. Аналогично муравьиному алгоритму, АВС ориентируется на поведение пчел при поиске и сборе пищи (нектара), но со своими особенностями.

Пчелы-разведчики вылетают на поиск наиболее богатых цветами мест в рамках определенной области в относительной близости от улья. При поиске пчела ориентируется на собственные наблюдения и после на наблюдения, сделанные другими пчелами. Одни и те же области облетаются несколько раз, постепенно выбор останавливаются между самыми цветочными. В итоге на наиболее подходящем месте пчела останавливается, и часть роя подлетает к ней для сбора нектара.

В АВС каждая условная пчела при движении ориентируется на лучшую позицию, определенную функцией пригодности. У всех пчел свои индивидуальные лучшие позиции, которые уточняются и меняются несколько раз при повторных разведках. То есть при пролете пчела сравнивает полученный ранее показатель с новыми данными и выбирает лучший. В итоге рой находит наилучшую позицию.

Вот несколько примеров его применения в реальной жизни:

1. Оптимизация расписания в различных сферах: например, в образовательных учреждениях алгоритм может помочь в оптимальном планировании занятий, распределении учителей и классов с учетом различных ограничений. Также в производственных системах он может помочь в распределении задач и ресурсов для повышения эффективности процессов.

2. Оптимизация маршрутизации и логистики. Например, в грузоперевозках или доставке товаров алгоритм может помочь в определении оптимальных маршрутов доставки с учетом различных факторов, таких как расстояние, время, пропускная способность дорог и ограничения.

3. Оптимизация распределения ресурсов в энергетических системах. Например, распределение генерирующих мощностей между различными источниками энергии, такими как солнечные батареи, ветряные турбины и гидроэлектростанции, чтобы достичь баланса между производством и потреблением энергии.

4. В задачах машинного обучения алгоритм роя пчёл может быть использован для оптимизации параметров моделей. Например, он может помочь в настройке гиперпараметров, таких как коэффициенты регуляризации, скорость обучения и число скрытых слоев в нейронных сетях.

5. Оптимизация распределения задач в параллельных вычислениях. Например, распределение вычислительных задач между процессорами или узлами вычислительного кластера для достижения баланса нагрузки и повышения производительности.

Алгоритм стаи серых волков

Алгоритм стаи серых волков или Gray Wolf Optimizer (GWO) также основан на модели поиска и добычи пищи, в данном случае — охоты волков. Но если в случае с муравьиным и пчелиным алгоритмами отдельные юниты действуют самостоятельно, не имея превосходящую или нисходящую роль в рое, то в GWO за основу берется сама структура волчьей стаи.

Четыре типа волков в стае имеют разное влияние в управлении и принятии решений: альфа наибольший вес, бета, дельта и омега по нисходящей соответственно. У каждого волка своя роль и привилегии в стае. Процесс добычи пищи проходит в несколько этапов: поиск, окружение и сама охота. В этом процессе каждый волк окружает потенциальную жертву и играет свою роль в охоте.

В GWO волки изначально распределяются случайным образом. Альфа, бета и дельта определяются близостью нахождения к условной жертве. Они окружают добычу, после чего в самом конце подступают омега-волки. Они движутся к геометрическому центру между положениями вышестоящих волков. После позиции всех волков обновляются в зависимости от положение каждого волка до тех пор, пока волки не доберутся к предполагаемому месту расположения добычи.

Вот несколько примеров его применения в реальной жизни:

1. Оптимизация параметров в алгоритмах машинного обучения. Например, помощь в настройке гиперпараметров моделей машинного обучения, таких как коэффициенты регуляризации, скорость обучения и число скрытых слоев в нейронных сетях.

2. Оптимизация распределения ресурсов в энергетических системах: определении оптимального распределения производства энергии между различными источниками, такими как солнечные панели, ветрогенераторы и гидроэлектростанции, чтобы максимизировать производство и снизить затраты.

3. Для кластерного анализа данных, когда требуется группировка объектов по схожести. GWO может помочь в нахождении оптимальных кластеров, учитывая сходство исходных данных и помогая в анализе данных и выявлении структуры.

4. Оптимизация портфеля инвестиций, то есть определении оптимального распределения инвестиций между различными активами, учитывая риск и доходность каждого актива, с целью максимизации прибыли и управления риском.

5. Оптимизация распределения задач в параллельных вычислениях. Например, алгоритм может помочь в определении оптимального распределения вычислительных задач между процессорами или узлами вычислительного кластера, чтобы достичь баланса нагрузки и повысить производительность системы.

Алгоритм летучих мышей

В основу алгоритма летучих мышей положена способность этих животных ориентироваться в пространстве благодаря эхолокации. Летучие мыши издают звуки высокой частоты, распространяющиеся по пространству, пока не столкнутся с какой-либо поверхностью и не отразяться от нее. По особенностям распространения и возврата эхо летучие мыши не только ориентируются в пространстве, но и определяют положение пищи или будущей добычи.

Условные летучие мыши в алгоритме изначально перемещаются случайным образом с определенной скоростью, издавая сигналы. Первые сигналы самые громкие. После определения оптимального решения (условной цели) громкость сигналов уменьшается, а частота наоборот — растет. Это решение играет роль нового положения летучей мыши и, если по определенным параметрам оно позиционируется как неподходящее, цикл с запуском сигналов повторяется снова, пока не будет определен оптимум.

Вот несколько примеров его применения в реальной жизни:

1. Оптимизация параметров в нейронных сетях. Например, он может помочь в настройке весов и смещений нейронной сети, чтобы достичь наилучшей производительности модели на заданной задаче, такой как классификация изображений или прогнозирование временных рядов.

2. Оптимизация распределения ресурсов в компьютерных сетях. Например, он может помочь в нахождении оптимального распределения нагрузки между серверами или оптимальном выборе маршрутов передачи данных с целью повышения производительности сети и снижения задержек.

3. Задача кластеризации данных, когда требуется группировка объектов по схожести. Алгоритм может помочь в определении оптимальных кластеров, основываясь на сходстве исходных данных, и помочь в анализе данных и выявлении структуры.

4. Оптимизация планирования ресурсов в производственных системах. Например, алгоритм может помочь в определении оптимальной последовательности производственных операций, распределении рабочих мест и оптимизации использования оборудования с целью повышения эффективности и снижения затрат.

5. Оптимизация функций в математических задачах, таких как поиск значения функции или решение задачи оптимизации с ограничениями.

Светлячковый алгоритм

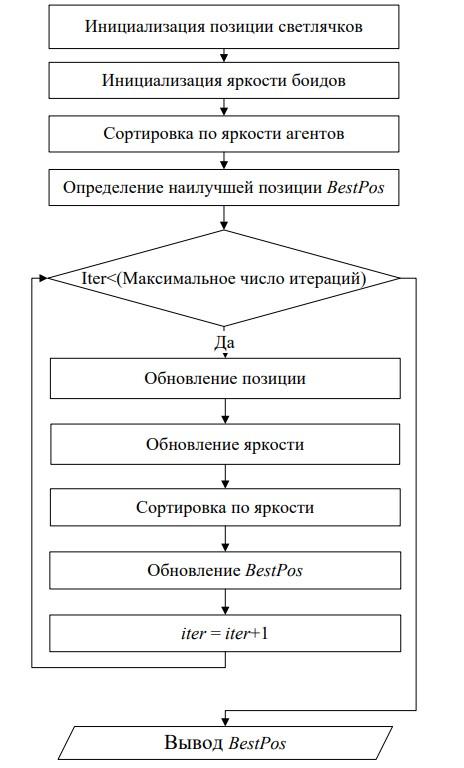
Светлячковый алгоритм сравнительно проще своих собратьев по роевому интеллекту. Он ориентируется на основные принципы, подсмотренные у поведения светлячков в природе. Эти насекомые излучают свет, что помогает им коммуницировать и привлекать особей противоположного пола. Светлячки всегда будут лететь к самым ярким и привлекательным собратьям.

В алгоритме условные светлячки изначально распределены случайным образом. У каждого из них кроме позиции есть значение яркости (оптимальное решение). Менее яркие светлячки будут тянутся к более ярким. Если светлячок ярче своих собратьев, он будет перемещаться случайным образом. После определенного числа итераций происходит вывод наиболее оптимального решения.

Вот несколько примеров применения этого алгоритма в реальной жизни:

1. Оптимизация маршрутизации в телекоммуникационных сетях, нахождение подходящих маршрутов для передачи данных, учитывая различные факторы, такие как пропускная способность, задержка и стоимость связи.

2. Оптимизация распределения ресурсов в системах энергоснабжения, например, распределение производства энергии между различными источниками, такими как солнечные панели, ветрогенераторы и гидроэлектростанции, чтобы достичь баланса между производством и потреблением энергии.

3. Оптимизация параметров моделей, настройка гиперпараметров моделей, таких как коэффициенты регуляризации, скорость обучения и число скрытых слоев в нейронных сетях.

4. Оптимизация планирования ресурсов в производственных системах, определение оптимального распределения рабочих мест, оборудования и материалов на производственных линиях для повышения эффективности производства и снижения затрат.

5. Оптимизация портфеля инвестиций между различными активами, учитывая риск и доходность каждого актива, с целью максимизации прибыли и управления риском.

Алгоритм кукушки

Кукушка известна своей привычкой подкидывать свои яйца в чужие гнезда, перекладывая ответственность по уходу за потомством на другие виды. Исследователи заложили эту особенность в основу разработанного алгоритма кукушки.

В данном алгоритме яйца, «подброшенные» в ограниченное число гнезд, представляют собой потенциальное решение задачи оптимизации. Наилучшие решения «выживают» и в последующем дают лучшее потомство, а гнезда с другими яйцами и менее приспособленными решениями опустошаются, оставляя только кукушек. Эти кукушки после вылетают и откладывают новые яйца в случайные гнезда. При достижении алгоритмом определенного предела цикл итераций (или поколений кукушек) прерывается.

Вот несколько примеров его применения в реальной жизни:

1. Оптимизация распределения ресурсов в сетях связи, размещение базовых станций или антенн для обеспечения лучшего покрытия с минимальными затратами.

2. Оптимизация планирования задач в распределенных системах, например, в облачных вычислениях или распределенных вычислительных средах, распределение задач между узлами сети для максимизации производительности и минимизации времени выполнения задач.

3. Для решения проблемы коммивояжера, поиск оптимального маршрута с использованием эвристического подхода, аналогичного поведению кукушек при выборе гнезда.

4. Оптимизация портфеля инвестиций, распределение средств между различными активами, учитывая риск и доходность каждого актива, с целью максимизации прибыли и управления риском.

Алгоритм оптимизации бактериального поиска пищи

Закончим подборку интересным алгоритмом глобальной оптимизации, нередко применяющимся для решения задач с повышенной сложностью. Алгоритм оптимизации бактериального поиска пищи (он же бактериальная оптимизация) берет за основу несколько типичных для бактерий особенностей поведения и реакций, в том числе хемотаксис — двигательную реакцию на химический раздражитель. В зависимости от реакции рецепторов бактерии либо движутся к источникам пищи, либо отдаляются от веществ, вызывающих негативную реакцию.

Классическая бактериальная оптимизация основывается на применении трех механизмов: хемотаксис, репродукция и рассеивание. В процессе хемотаксиса происходит движение бактерий, отдаляющие их от нежелательных веществ и приближающие к пище. После бактерии начинают роиться, расти и делиться в наиболее благоприятных местах, образуются новые особи. Рассеивание заключается в миграции группы в новое место с подходящим источником пищи. При этом на всех этапах проходит ликвидация наиболее слабых особей. 

Вот несколько примеров вариаций алгоритма с основными принципами.

•  Алгоритм колонии бактерий (Bacterial Colony Algorithm):

  • Инициализация колонии бактерий с заданным количеством бактерий.

  • Каждая бактерия имеет свои координаты в пространстве решений и оценку своей приспособленности (функцию приспособленности).

  • Каждая бактерия имеет своё собственное направление движения на основе приспособленности и расстояния до других бактерий, обновления координат в направлении движения с учетом случайного шума и вычисления новой оценки приспособленности.

  • Повторение шагов до достижения условия остановки (например, определенного количества итераций или достижения требуемой точности).

  • Возвращение лучшей найденной бактерии в качестве решения задачи оптимизации.

• Алгоритм хемотаксиса (Chemotaxis Algorithm):

  • Инициализация колонии бактерий и источника питания.

  • Каждая бактерия имеет свои координаты в пространстве решений и оценку своей приспособленности.

  • Каждая бактерия выполняет следующие шаги:

  • Определение градиента концентрации пищевого источника в текущей позиции.

  • Вычисление новых координат, двигаясь в направлении градиента концентрации.

  • Обновление оценки приспособленности.

  • Повторение шагов до достижения условия остановки.

  • Возвращение лучшей найденной бактерии в качестве решения оптимизационной задачи.

• Алгоритм колоний (Colonial Algorithm):

  • Инициализация нескольких колоний бактерий с разными параметрами (например, начальные координаты, размер шага и т. д.).

  • Каждая колония бактерий выполняет шаги, аналогичные алгоритму колонии бактерий.

  • Периодически происходит обмен информацией между колониями, где лучшие бактерии передают свои позиции и оценки приспособленности другим колониям.

  • Процесс повторяется до достижения условия остановки.

  • Возвращение лучшей найденной бактерии из всех колоний в качестве решения задачи оптимизации.

Вот несколько примеров из реальной жизни, где применялись алгоритмы оптимизации, основанные на бактериальном поиске пищи:

1. Оптимизации маршрутов доставки товаров в логистической сфере. Каждая «бактерия» представляет собой поставщика и имеет свои координаты в пространстве маршрутов, взаимодействует и обменивается информацией с другими, чтобы найти оптимальные пути доставки, учитывая различные факторы (расстояние, время, пропускная способность дорог и не только)

2. Оптимальное размещение сенсорных узлов. Каждый узел представляет собой «бактерию» и движется в направлении более сильного сигнала или источника данных, что позволяет эффективно распределить узлы для обеспечения максимального покрытия и связности сети при минимальной энергопотребляемости.

3. Оптимизация дизайна структур, таких как здания, мосты или автомобильные кузова. Бактерии моделируются в виде частиц, перемещающихся и взаимодействующих с окружающей средой с целью поиска оптимальной конфигурации, учитывая прочность, стабильность и другие параметры проектирования.

4. Оптимальное распределение ресурсов в системах управления энергопотреблением. Каждая «бактерия» представляет собой потребителя энергии и выбирает оптимальный путь или стратегию для максимизации энергоэффективности системы, учитывая ограничения и целевые показатели.

Есть и другие алгоритмы, в названии которых фигурируют животные. Но часть из них никак не связана с реальным поведением животных в природе. Например, алгоритм черепахи и зайца отсылает к известной басне о гонке между двумя животными. В случае с алгоритмом кенгуру Полланда — это первое название алгоритма, отсылающее к аналогии, используемой автором научной статьи для описания (использование ручного кенгуру для поимки дикого).