Одним из важнейших направлений работы над моделями машинного обучения является их оптимизация. Оптимизированная модель работает быстрее, требует меньше вычислительных ресурсов, и как следствие — снижает себестоимость работы ПО, использующего модель. Для задач, когда существует ограничение по типам изображений при использование генеративных моделей, возможный путь оптимизации — дистилляция существующих "больших" универсальных моделей. Например, Stable Diffusion (Далее — SD).

Также для некоторых задач, связанных с демонстрацией пользователям изображений, необходимо как можно скорее выводить результат генерации.

Таким образом, нашей целью является сокращение издержки на аренду серверов с GPU и уменьшение времени генерации при незначительной потере качества. Одним из возможных вариантов оптимизации SD является метод дистилляции.

Идея дистилляции предложена Дж.Е. Хинтоном и В.Н. Вапником¹. Суть идеи состоит в обучении более простых моделей на основе поведения более сложной на изначально определенной выборке данных. При этом модель с большим числом параметров называется учителем, а модель, получаемая путем дистилляции, называется учеником. Изначальным предложением являлось использовать ответы учителя в качестве целевой переменной для обучения модели ученика. Эксперименты показали возможности результативной дистилляции моделей не только для одной модели, но и для ансамбля моделей, дистиллируемого в одну, более простую. В качестве критерия обучения дистиллированных моделей можно использовать:

— минимизацию специальной функции потерь, основанной на вычислении максимального среднего отклонения между выходами всех слоев модели учителя и ученика,

— приведение пространства параметров ученика к пространству параметров учителя, основанное на байесовском выводе.

В изначальной постановке Хинтона дистилляция представляет собой общее решение для получения вероятностных распределений мягких целей. При этом вероятности создаются с помощью функции активации softmax, которая преобразует логиты z_i и рассчитывается для каждого класса в вероятности q_i:

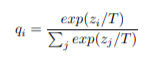
Здесь T — это температура распределения softmax, множитель, который позволяет регулировать соотношение между уверенностью предсказания модели и её разнообразием. Использование высокой температуры приводит к более мягкому распределению вероятностей.

В простейшей форме дистилляции знания передаются дистиллированной модели путем обучения её на набор переноса и использование мягкого целевого распределения для каждого случая, созданного с использованием модели с высокой температурой softmax. Такая же высокая температура используется при обучении дистиллированной модели. Когда известны правильные метки для всего или части набора переноса, этот метод может быть значительно эффективнее.

В диапазоне высоких температур дистилляция эквивалентна минимизации половины обратного квадрата расстояния между целями, при условии, что логиты изначально имеют нулевое значение. При более низких температурах дистилляция работает гораздо медленнее за счет сопоставления логитов, в этом случае имеющих меньшие значения. С другой стороны, во втором случае логиты не ограничены функцией стоимости и могут передавать полезную информацию из модели учителя. Какой из эффектов выгоднее использовать, решается обычно эмпирическим способом.

Альтернативным способом дистилляции является использование средневзвешенного значения двух различных целевых функций. В качестве первой целевой функции здесь обычно берётся кросс-энтропия для мягких целей, вторая — кросс-энтропия для правильных меток.

Рассмотрим идею дистилляции моделей на основе байесовского вывода. Пусть задана выборка

где (Xi, Yi) — признаковое описание и целевая переменная i-го объекта. При этом, для модели учителя будем пользоваться суперпозицией линейных и нелинейных преобразований

f(T, F, Ui) — где T — число слоев модели учителя, F — функция активации, Ui — i-я матрица линейного преобразования.

Каждая матрица преобразования имеет размер, соответствующий поставленной задаче — в случае регрессии финальная матрица будет иметь размер 1, в случае классификации — k. Для построения вектора параметра u задается полный порядок на элементах матриц Ui. Пусть для вектора параметров u учителя известно апостериорное распределение параметров p(u|D). Тогда на основе выборки D и апостериорного распределения параметров выбираем модель ученика из параметрического семейства функций g(L, F, Wj), где L — число слоев модели ученика. При этом, задача выбора модели g эквивалентна задаче оптимизации вектора параметров w. Параметры вектора оптимизируются при помощи вариационного вывода на основе совместного правдоподобия модели и данных.

Апостериорное распределение параметров модели учителя предполагается нормальным. Параметры априорного распределения ученика приравниваются к параметрам апостериорного распределения учителя в случае выполнения следующих условий:

1. Число слоёв модели ученика равняется числу слоев модели учителя.

2. Размеры соответствующих слоёв совпадают.

Модификация модели ученика в этом случае осуществляется с помощью следующих действий:

1. Удаление нейрона в слое.

2. Удаление слоя нейронов.

Согласно некоторым исследованиям², считаем, что модели ученика с заданием априорного распределения параметров на основе апостериорного распределения параметров учителя сходятся быстрее.

Рассмотрим в общем случае задачу дистилляции моделей для генерации изображений. Оптимизация параметров сетей, используемых в рамках процесса генерации изображений по их текстовому описанию, осуществляется, как правило, на основе целого набора критериев, включающего в себя как точность и безошибочность работы модели, так и технические характеристики работы модели, такие, как требуемые вычислительные ресурсы, время работы и т.д. Соответственно, целевая функция оптимизационной модели является комбинацией вышеперечисленных критериев, в то время, как задаваемые ограничения обычно имеют характер пользовательских и технических пожеланий и зависят от предметной области, а также от имеющихся вычислительных ресурсов.

Формирование моделей, используемых для генерации изображений, в настоящее время целесообразно осуществлять с помощью инструментального пакета Stable Diffusion, созданного на основе аппарата генеративных нейронных сетей и ориентированного на использование с привлечением относительно небольшого количества вычислительных ресурсов. Основной функциональностью пакета Stable Diffusion является генерация изображений на основе текстового описания. Несмотря на изначальную ориентированность на относительно небольшое количество используемых вычислительных ресурсов, быстродействие изначальных, «универсальных» моделей Stable Diffusion оставляет желать лучшего, поэтому важнейшим направлением, определяющим использование Stable Diffusion на практике, является использование различных методов дистилляции, разработанных на основе анализа существующей предметной области и позволяющих понизить сложность аппроксимирующих моделей. Особенно актуальным является использование дистилляции в случаях, когда изначальная генерация осуществляется с использованием ансамбля моделей.

В качестве базовой структуры сети для генерации изображений наиболее рационально использовать вариант архитектуры UNet, представляющей собой сверточную сеть, изначально предназначенную для сегментации изображений. Архитектура сети представляет собой последовательность слоёв свёртки, которые сначала уменьшают пространственное разрешение картинки, а потом увеличивают его, предварительно объединив с данными картинки и пропустив через другие слои свёртки. Таким образом, сеть выполняет роль своеобразного фильтра.

Обучение такой сети ведется методом стохастического градиентного спуска на основе входных изображений и соответствующих им карт сегментации. Из-за сверток выходное изображение меньше входного сигнала на постоянную ширину границы. Применяемая попиксельно, функция soft-max вычисляет энергию по окончательной карте свойств вместе с функцией кросс-энтропии. Кросс-энтропия, вычисляемая в каждой точке, определяется так:

Граница разделения вычисляется с использованием морфологических операций. Затем вычисляется карта весовых коэффициентов:

где wc — карта весов для балансировки частот классов, d1 — расстояние до границы ближайшей ячейки, а d2 — расстояние до границы второй ближайшей ячейки.

Таким образом, получаем набор обученных моделей, которые можно использовать как по отдельности, так и в виде ансамбля для генерации фотореалистичных изображений. Однако, для практического использования необходима дистилляция моделей, которая позволит справиться со следующими проблемами:

1. Требовательность к ресурсам и невысокая скорость работы сети (не в режиме реального времени).

2. Создание нереалистичных изображений.

Результирующие модели должны быть достаточно легковесны и учитывать в работе только те классы предметов, которые используются в системе. Соответственно, процесс дистилляции\настройки должен периодически актуализировать данные и переобучать модели, используемые на практике.

Рассмотрим технические пути оптимизации сетей для их удовлетворительного функционирования в рамках промышленного сервера. Одним из путей оптимизации нагрузки является использования знания о том, что пакет Stable Diffusion использует для своей работы ансамбль сетей, на первом уровне которого стоит семантический токенайзер запросов. Учитывая, что количество вариантов, на основе которых осуществляется генерация изображений, для нашего приложения ограничено считанным количеством вариантов, возможным решением является ограничение размера вариантов до длины 10-12 слов. Таким образом, у нас появляется возможность выполнить предварительную токенизацию вариантов, сохранить полученные вектора в БД и таким образом избавить процесс генерации от работы токенизирующего модуля.

Данный подход оптимизирует генерацию в плане сокращения объема занимаемой памяти GPU (лингвистическая модель занимает порядка 1,5 Гб и находится в памяти перманентно), а также сокращает общее время генерации.

Ещё одним путем повышения быстродействия сети является использование детектора бинарного вектора признаков на изображениях с тематических ресурсов. Вводя инструменты контроля за результатом работы генерирующего алгоритма, мы можем существенно очистить изначальный массив данных, что, безусловно, потребует меньше ресурсов для сети, получающейся в итоге дистилляции.

Непосредственно для генерации картинок из диффузных моделей был выбран процесс, основанный на использовании сети архитектуры UNet, обладающей весьма привлекательными техническими характеристиками и качеством результата. Для учета текстового описания используется Text Encoder из модели CLIP.

CLIP³ — модель от OpenAI, которая обучалась на изображениях и их описаниях из интернета. Основная прелесть в том, что она отображает картинки и тексты в единое векторное пространство. Это позволяет измерять близость между картинками и текстами.

Энкодер принимает на вход картинку в виде тензора (1, 3, 512, 512), где 1 - размер батча, 3 - RGB-кодировка. Возвращает латентное (сжатое) представление — тензор размерности (1, 4, 64, 64).

Декодер принимает на вход тензор из латентного пространства и восстанавливает исходную картинку с некоторой точностью. В результате имеем сеть, которая умеет сжимать и разжимать картинки.

Отображение картинки в латентное пространство с помощью энкодера выполняется с помощью следующего кода на языке Python:

def preprocess(pil_image):
    pil_image = pil_image.convert("RGB")
    processing_pipe = transforms.Compose([
        transforms.Resize((512, 512)),
        transforms.ToTensor(),
        transforms.Normalize([0.5], [0.5]),
    ])
    tensor = processing_pipe(pil_image)
    tensor = tensor.reshape(1, 3, 512, 512)
    return tensor
def encode_vae(img):
    img_tensor = preprocess(img)
    with torch.no_grad():
        diag_gaussian_distrib_obj = vae.encode(img_tensor.to(device), return_dict=False)
        img_latent = diag_gaussian_distrib_obj[0].sample().detach().cpu()
        img_latent *= 0.18215
    return img_latent
image_latent = encode_vae(your_img)
image_latent.shape
> torch.Size([1, 4, 64, 64])

Декодирование, соответственно, выполняется
следующим способом:

def decode_latents(latents):
    latents = 1 / 0.18215 * latents
    with torch.no_grad():
        images = vae.decode(latents)['sample']
    images = (images / 2 + 0.5).clamp(0, 1)
    images = images.detach().cpu().permute(0, 2, 3, 1).numpy()
    images = (images * 255).round().astype('uint8')
    pil_images = [Image.fromarray(image) for image in images]
    return pil_images
images = decode_latents(image_latent.to(device))
images[0]

В наших условиях для генерации по условию необходимо использовать реализацию Unet2dConditionModel, которая отличается от базовой количеством измерений на входе и набором слоев. Существенную роль играет подбор планировщика шума, работа которого серьёзно влияет на качество генерации.

Использование структуры Unet2DConditional для генерации изображений через ансамбль методой Stable Diffusion является одним из перспективных практических направлений, способных удовлетворить потребности разрабатываемого сервиса с точки зрения как технических, так и пользовательских характеристик. Развитие практики генерации изображений может идти как в направлении поиска более эффективных методов дистилляции, так и в области построения эффективной динамической архитектуры потоков данных, обеспечивающих эволюционный подход к созданию моделей и алгоритмов диффузной генерации данных.

В результате дистилляции нами были получены следующие результаты:

1. Снижение размера используемой модели до 360 Мб (оригинальный не обученный Stable Diffusion имеет размер более 12 Гб).

2. Уменьшение времени генерации изображений с 3,5 секунд до менее чем 1 секунды.

3. Потеря качества генерации при этом незначительна. Примеры показаны ниже.
   

Рисунок 1. Генерация при помощи модели runwayml/stable-diffusion-v1-5

Рисунок 2. Генерация при помощи модели, полученной после дистилляции.

Модель генерации, дистиллированная под конкретные задачи позволяет обеспечить высокую скорость выдачи вариантов генерации, что позволяет дольше сохранять «фокус внимания» пользователей.