Блок 1: не то, чем кажется
Начнем немного издалека: так уж сложилось, что наш глаз видит яркости окружающего мира в нелинейной кривой. Там, где в реальном мире яркость одного объекта может быть больше другого в 2 раза, для нашего глаза разница в яркости может показаться иной. Для наглядной проверки достаточно взглянуть на обычный линейный градиент:

Для подтверждения, вот так выглядит вейвформа изображения:

Абсолютно линейный градиент от 0 до 100 нит.
В каком месте вы лучше видите изменение яркости? В левой или правой части? Для упрощения задачи давайте разобьем градиент на несколько сегментов с одним оттенком у каждого сегмента

И взглянем на его левую:

И правую части:

Думаю большинство ответило, что в левой части изменение оттенков более заметно, чем справа. Это подводит нас к мысли, что абсолютно линейной изменение яркости наш глаз видит нелинейно: изменение яркости в темных оттенках заметно лучше, чем в светлых. Если мы попробуем выразить эту зависимость изменения яркости для глаза (ось Y) от действительных значений (ось X), то на выходе получим примерно вот такую кривую:

Поздравляю, мы только что простым экспериментов вывили примерную яркостную кривую, в которой наше зрение воспринимает окружающий мир. Если мы теперь целенаправленно поищем в интернете, в какой наш глаз видит кривой, то найдем похожие изображения, которые подтвердят наш эксперимент:

Эта кривая близка к функции гаммы 2.2:
y = x^(1/«gamma value»)
Да да, а вы что думали, матан в жизни не пригодится?
Поэтому там, где программа показывает 0.218, нам кажется, что там четкие 0.5.
При отображении линейной зависимости для нашего глаза в тенях на 1 стоп экспозиции будет приходиться буквально несколько единиц изменения значений rgb. Тогда как в светлых участках на 1 стоп приходится 128 единиц rgb -> нерациональное использование памяти

Выводы на данный момент:
Наш глаз видит мир нелинейно
В тенях мы видим изменение яркости лучше, чем в светлых участках
Блок 2: И овцы целы, и волки сыты
Имея вышеперечисленные знания можно предположить: а ведь не самой лучшей идеей будет записывать цифровые изображения в линейную кривую. Ведь для того, чтобы сохранить достаточно деталей в темных участках, нам придется применять бОльшую битность, тратить большое памяти, так еще и ко всему этому записывать бесполезные для нашего глаза детали в ярких участках. И тут на помощь приходит кодирование в некую яркостную кривую. Почему в «некую»? А потому что хрен их там разберет, какая камера в какую конкретно пишет, и вообще все это настолько часто менялось, что там уже не чистая гамма кривая, а некая кусочно-заданная функция. Но для упрощения понимания, давайте будем называть ее «гамма 2.2». И вот как раз эта гама кривая позволяет эффективно использовать возможности камеры и с меньшей битностью записывать изображения, сохраняя бОльшее количество деталей в темных участках, и меньшее в светлых. Эта коррекция называется OETF
Но теперь, когда в файл изображения вшита корректирующая гамма-кривая, при отображении на мониторе картинка будет банально пересвечена. Поэтому, во всех ваших мониторах, телефонах, телевизорах встроена обратная гамма функция, обратная той, что была в камере:
y = x^«gamma value»
для того, чтобы нейтрализовать гамму-коррекцию в файле. Поэтому на выходе получаем нормализованные яркости, как в реальном мире.
Сделаем выводы:
записывая изображение с применением гамма-кривой, мы можем эффективно сохранять детали для нашего глаза
для корректного отображения таких файлов в устройстве просмотра применяется обратная гамма-функция
Блок 3: про работу в линейном пространстве
Ладно, с энкодингом и декодингом разобрались, но зачем нам надо работать в линейной кривой?
И не опять, а снова, будем все познавать на примерах. Допустим, на входе имеем солид со значениями по всем 3-м каналам в 0.2.

Если мы работаем в нелинейной кривой, то при увеличении значения в 2 раза мы получим… значение примерно 0,93.

Согласитесь, не совсем то, что нам нужно было.
Теперь же умножим на два исходник, работая в линейной кривой:

Теперь мы получили желаемое значение в 0,4.
Основываясь на простом факте, что банальное умножение в нелинейной кривой уже работает некорректно, выдавая нам неверные значения, и вспоминая, что цифровой композ - это все одна большая математика с обильным применением матриц, в которых применяется умножение, просто представьте, какая вакханалия будет твориться при работе в нелинейной кривой. По одному месту пойдут все фильтры, будь то блюр, глоу и прочие. ВСЕ, что использует математику как инструмент(то есть вообще все) будет работать неправильно.
Обобщаем
Камера видит мир в линейной зависимости, наш глаз - в нелинейной
Исходя из особенностей нашего зрения, записываем изображение с кодированием кусочной функцией sRGB для эффективного использования данных (много инфы в тенях - мало в светлых участках)
При простом просмотре на мониторе применяем обратную гамма-коррекцию, возвращающую яркостную зависимость к линейному виду. При обработке переводим изображение в линейное пространство, корректируем, после возвращаем исходную гамму-кривую.
Причина применения гамма-коррекции:
Эффективное хранение данных
Причина работы в линейном пространстве:
Корректная обработка с использованием математических операций
Источники:
https://www.gdcvault.com/play/1012351/Uncharted-2-HDR
https://chrisbrejon.com/cg-cinematography/introduction/
https://www.youtube.com/watch?v=zBawwb6L9bo
https://www.youtube.com/watch?v=WJzmcJQFlao
https://www.youtube.com/watch?v=vRG6o-UII8k&t=547s
https://color.viewsonic.com/explore/content/Accurate-Gamma_4.html
https://wiki2.org/ru/Гамма-коррекция
https://habr.com/ru/post/353632/
https://en.wikipedia.org/wiki/Gamma_correction#Explanation
https://www.cambridgeincolour.com/ru/tutorials-ru/gamma-correction.htm
Комментарии (4)

Tolkik
24.08.2023 15:00+1Брехня. Даже не стал читать статью, проверил в фотошопе первую картинку - это никакой не линейный градиент. Картинка 1000 пикселей ширины, значит каждые 10 пикселей значение "черноты" должно меняться на 1%. По факту слева первый пиксел 100% черноты десятый пиксел уже 93% черноты, хотя должен быть 99%. А справа наоборот: крайний правый пиксел 0% черноты, а через 100 пикселей 6%, хотя должно быть 10%. Картинка явно засвечена.
Вот настоящий линейный градиент и никаких резких переходов не видно, если что-то видно, то это уже дефекты цветопередачи вашего монитора.

Tarakanator
24.08.2023 15:00+2Так монитор же выводит с учётом гамма кривой. Так что это у вас не линейный градиент. А ТС как я понял сделал картинку так, чтобы с учётом гаммы монитора сделать линейный градиент.

viruseg
24.08.2023 15:00+1Откуда вообще берутся такие юзеры на хабре. И кто-то плюсует комментарий.
Под рукой в данный момент открытая unity. Создал простейший шейдер, который берет uv координаты и выводит x. Т.е. на выходе линейное изменение от 0 до 1. Но вообще такое даже проверять глупо. Всё равно, что подвергать сомнению высказывание "земля круглая".
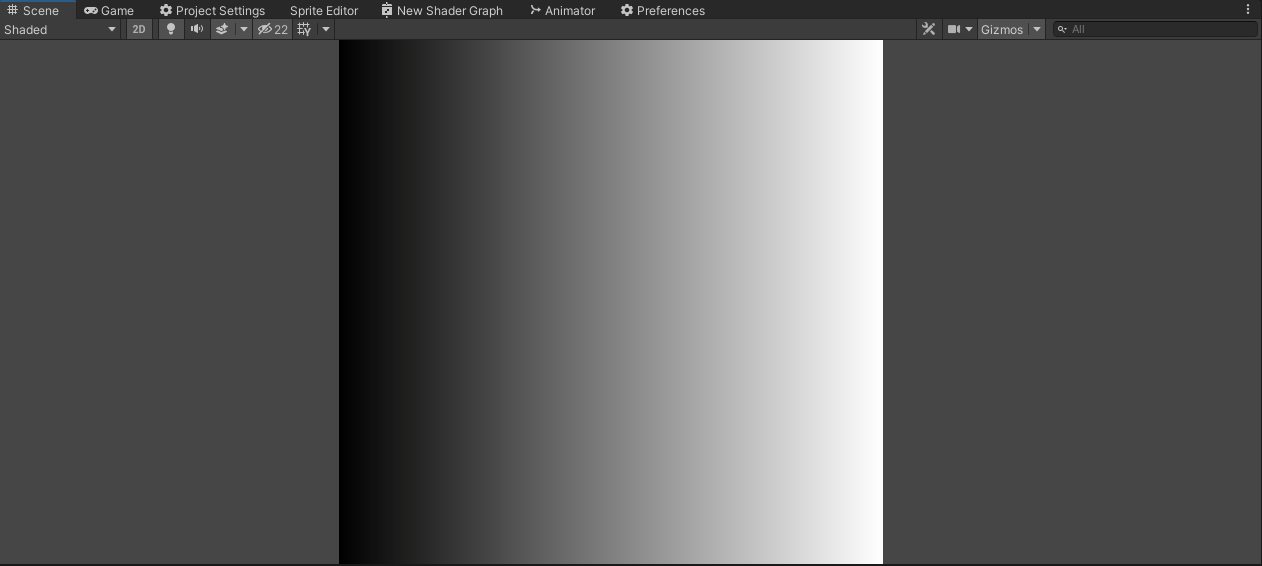
Результат 
Шейдер 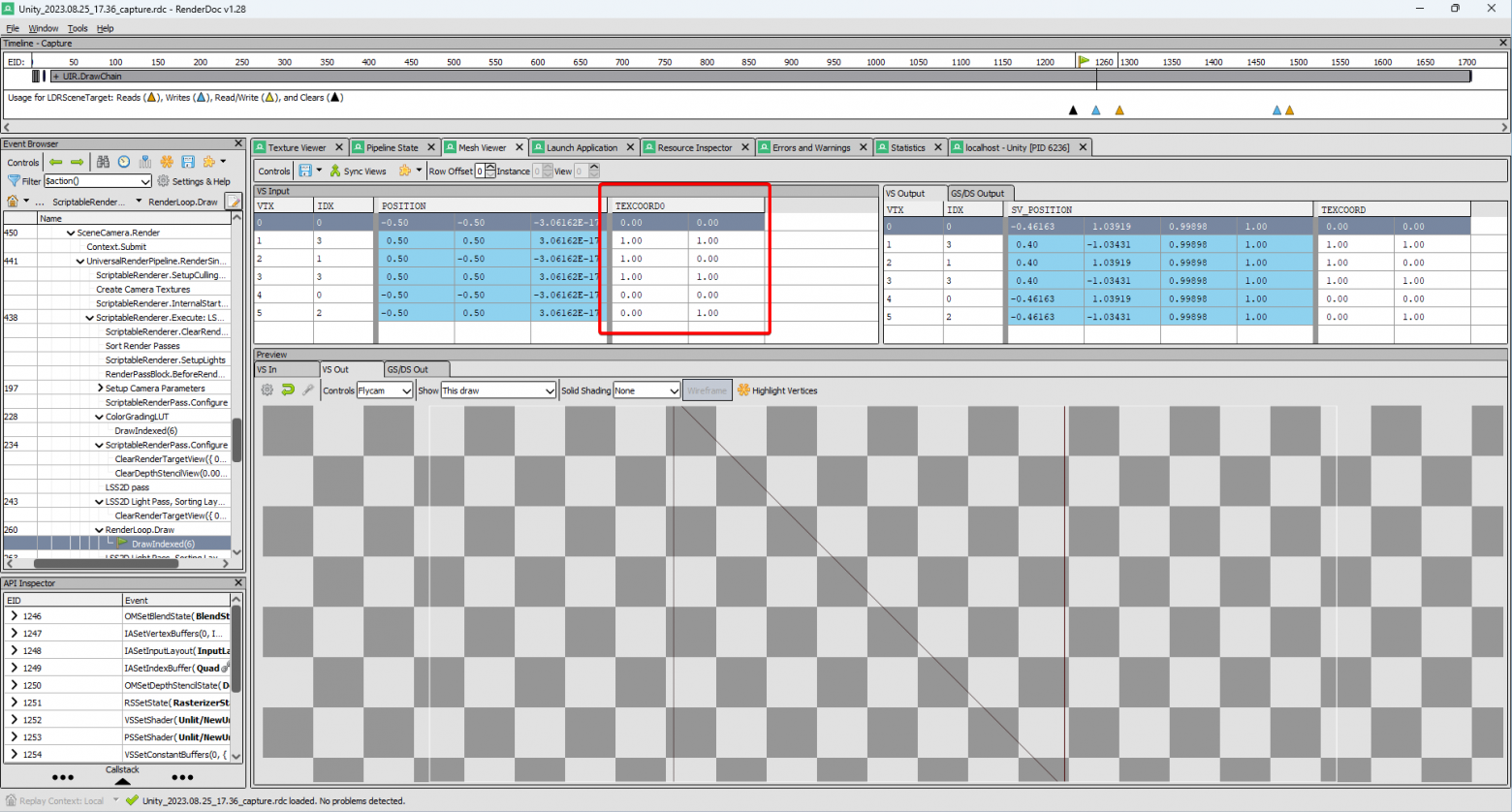
Скрин того, что лежит в uv. Чтобы не было сомнений. А вот с гамма-коррекцией:

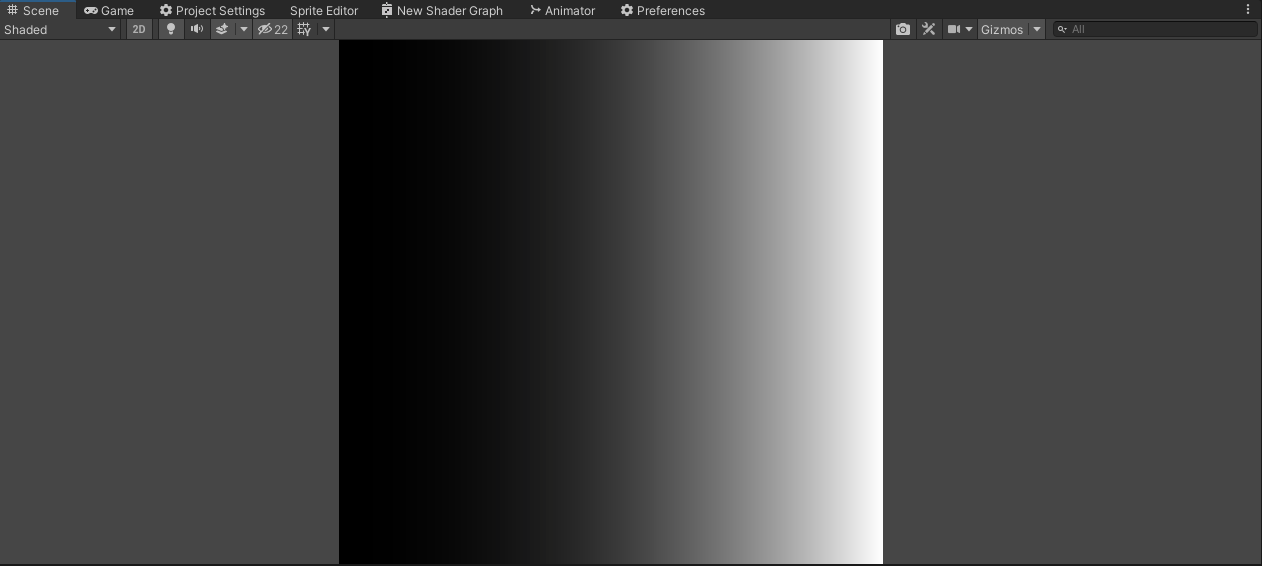








iShrimp
О гамма-коррекции следует помнить каждому, кто имеет хотя бы какое-то отношение к компьютерной графике. Потому что гамма - это не просто костыль для хранения цвета. Она порождает множество костылей в самых разных сферах, от дизайна шрифтов (сколько боли и мучения требуется, чтобы заставить текст выглядеть одинаково на белом и на чёрном фоне) до разработки шейдеров для 3d-графики.
Если когда-нибудь индустрия придёт к повсеместному внедрению 16-битной глубины цвета, то это даст возможность решить проблему на корню, сделав гамму линейной на всех устройствах.
Проблемы с гаммой наиболее заметны на тонких светлых линиях на тёмном фоне.