Динамическое ценообразование является современным подходом к ценообразованию в ритейле. Оно напрямую связано с моделированием спроса, что позволяет проводить оптимизацию цен на будущий период. В этой задаче популярным решением является использование машинного обучения, однако, все ли так хорошо в этом королевстве? На самом деле применение ML в этой задаче сталкивается с рядом проблем, которые не просто решить, например, когда в исторических данных цена на товар никогда не менялась. Одним из возможных решений является использование reinforcement learning (RL). В этой статье мы рассмотрим нюансы такого подхода и постараемся понять, а стоит ли оно вообще того? В качестве RL модели будет использоваться Thompson Sampling.

Я не буду останавливаться подробно на том, как работает ST, поскольку про этот подход писали уже неоднократно, и я не вижу смысла повторяться - можно прочитать на Хабре тут, тут и тут. Разница между рекомендацией контента и задачей выбора оптимальной цены заключается в том, что вместо выбора картинки котика, которую нужно показывать пользователям, мы выбираем цену, которую нужно установить на товар. Подробнее про такой подход можно почитать, например тут.

Зачем тут вообще многорукие бандиты?

Описанный подход на основе ML страдает от нескольких проблем, связанных с особенностями самой задачи динамического ценообразования:

• Оптимизация цен для новых товаров. Ротация линейки товаров приводит к тому, что постоянно появляются новые товары, которые не имеют исторических данных по продажам. Оптимизировать цены по таким товарам тоже нужно, однако подход ML, основанный на моделировании исторических данных, сталкивается с проблемами, из-за полного отсутствия этих самых исторических данных.

• Высокая разреженность данных. Множество товаров на практике продаются не каждый день, поэтому, на уровне SKU (товарной позиции) красивых временных рядов с явной сезонностью в данных будет не так много. Зато будет много товаров, которые продаются по 1-2 штуки в неделю или даже в месяц. Это приводит к низкому соотношению сигнал/шум в данных, что затрудняет использование ML, да и какого-либо вообще другого подхода.

• Низкая вариативность цен в исторических данных. Чтобы определить, как изменение цены конкретного товара влияет на спрос этого же самого товара, необходимо иметь в исторических данных хотя бы две разные цены. На практике множество товаров может иметь одну единственную цену за весь период наблюдений. В таком контексте определить эластичность по цене классическими методами становится невозможно.

• Постоянный дрифт в данных. Кажется это классика, однако все дело в скорости дрифта. Рыночные условия могут меняться достаточно быстро из-за социально экономических потрясений, всплесков инфляции и других факторов. В итоге пока мы наберем исторические данные о новых условиях, чтобы обучить на них ML модель, они уже успевают измениться и новая модель становится неприменимой.

• ML “застревает” на субоптимальных решениях. В первую очередь это связано с тем, что решения, принятые на основе ML, влияют на обучающую выборку, которая будет сформирована в будущем. В итоге модели влияют сами на себя и впадают в цикл подтверждения ранее принятых решений. Иными словами, один раз выставив субоптимальную цену, оптимизация будет иметь тенденцию раз за разом устанавливать ту же самую цену, неспособную приблизиться к истинному решению.

Этот пул проблем имеет некоторый набор стандартных “лекарств”, которые призваны минимизировать описанные явления. Однако, давайте посмотрим на радикальный метод лечения с использованием многоруких бандитов. Для данной статьи мы будем рассматривать Сэмплирование Томпсона, поскольку этот подход является наиболее эффективной альтернативой из всех вариантов многоруких бандитов.

Сэмплирование Томпсона для ценообразования на практике

В общем виде модель выглядит не такой уж и сложной для понимания. Она является итеративной, и ее применение состоит из нескольких этапов внутри каждой итерации. Чтобы разобраться, какие существуют нюансы применения ST, будем разбирать модель поэтапно.

Выбираем характер зависимости спроса от цены

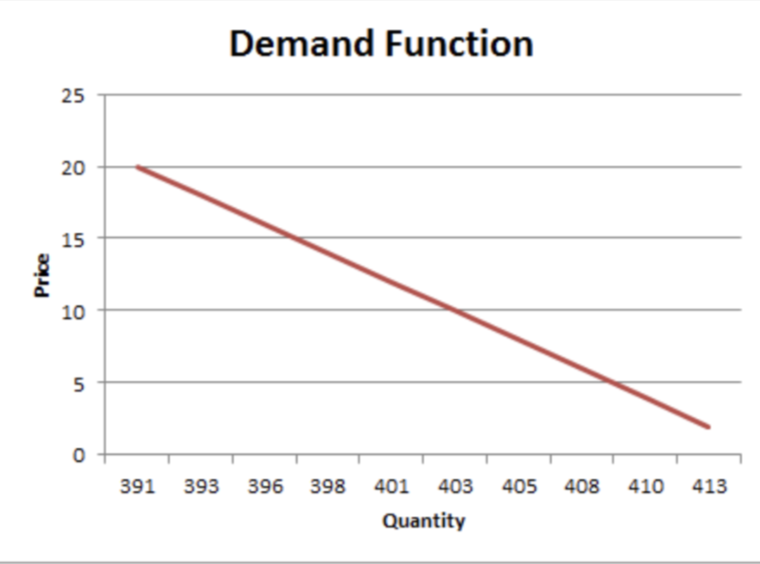
Самым базовым выбором для классического ML в ценообразовании является линейный характер зависимости спроса от цены. Именно такую зависимость между ценой и спросом можно встретить в значительном количестве микроэкономических моделей.

Нюанс 1: дискретная модель спроса

Однако для Сэмплирования Томпсона такой характер зависимости не является выбором по умолчанию, потому что в самой сути модели заложена дискретность выбора какого-то одного, оптимального варианта (самой прибыльной ручки бандита из нескольких).

В случае ценообразования модель ST ищет оптимальную цену среди нескольких возможных вариантов. Это приводит к тому, что в варианте “по умолчанию” алгоритма ST используется дискретная модель спроса, которая предполагает, что для каждой цены у нас свой спрос, и величина спроса между ценами никак не коррелирует между собой.

Очевидным плюсом такого подхода является то, что спрос может не быть непрерывной величиной и могут наблюдаться резкие скачки спроса при преодолении каких-либо психологических уровней. Также на руку этой модели играет то, что маркетологи любят ставить не какой-то случайный набор цен, а цены с красивыми округлениями, например, “*.99”, что может быть удобно использовано в этой модели.

Однако есть и ряд минусов. Для нас, как пользователей этой модели, дискретная модель означает, что если мы собрали исторические данные о спросе по цене P1, то модель никак не сможет их применить для прогнозирования того, какой спрос будет по цене Р2, пока эта цена не будет установлена на практике и не будет измерен спрос (что мы можем сделать сами и без моделей).

Дискретный характер зависимости может быть довольно оправданным решением в рекомендательных системах для контента, потому что лайки одной картинки с котиком никак не коррелируют с лайками другой картинки с котиком, однако для вопроса ценообразования этого становится несколько... недостаточно. 

Дискретная модель спроса - это самый базовый вариант, который не учитывает такие факторы спроса, как сезонность, промо, каннибализм между товарами и так далее. Если не учитывать все эти факторы, то распределение возможного спроса для каждой цены останется достаточно широким, сколько бы итераций уточнения на основе реальных данных не произошло. Также, из предпосылки дискретной функции спроса следует множество технических ограничений модели, с которыми мы столкнемся далее.

Нюанс 2: а сколько разных цен мы можем установить?

Будем придерживаться практичности и предположим, что возможный диапазон новых цен будет +/-10% от некоторой текущей цены. Давайте предположим, что шаг цены может быть равен 1 копейке (пока что забудем про округления). Тогда, если базовая цена составляет 100 рублей, то установить мы можем цены в диапазоне 90-110, а это, как нетрудно посчитать, 2 000 возможных вариантов цен. Теперь вспоминаем про дискретную модель спроса (нюанс 1), и получаем 2 000 никак не связанных между собой моделей. Если мы захотим по одному разу поставить каждую цену хотя бы на один день, то получаем 5,5 лет мучений выбора оптимальной цены для этого товара. Не очень хорошо! 

Чтобы избежать такой ситуации, нужно серьезно сокращать количество цен, которые можно выставить. Тут идут в ход всеми любимые округления до х.99, х.45, что значительно снижает коллекцию из 2 000 цен до нескольких десятков.

Тем не менее, если мы разобрались для товара с ценой 100 рублей, то для товара с ценой 1 000 рублей решить проблему становится сложнее: с шагом в 1 копейку, в диапазоне +/-10% уже не 2 000 возможных цен, а 20 000! Решать такое возможно только либо скрупулезной проработкой возможных цен для установки, либо алгоритмами, которые автоматически выбирают цены с некоторым %-ным шагом, соблюдая правила округления. Ценой за такой подход является ширина пробелов между возможными ценами: вместо того, чтобы пробовать 1 010, 1 019, 1 029 … 1 099, на практике становится возможным опробовать перечень гораздо уже, например 1 000, 1 049, 1 099. Это все сказывается на точности выявления оптимальной цены. Например, если истинно оптимальная цена будет 1 079, то мы этого уже не узнаем, а сможем установить только самую ближайшую к ней - 1 099, даже если это приведет к уменьшению ожидаемой выручки/прибыли. Для целей данной статьи установим упрощенный возможный перечень цен: [1.99, 2.49, 2.99, 3.49, 3.99, 4.49, 5.99].

Нюанс 3: какое вероятностное распределение выбрать?

В модели ST предполагается, что спрос - это вероятностная величина, то есть для одной цены спрос может варьироваться в некотором диапазоне (см. серую гистограмму на графике слева).

На графике представлена гистограмма спроса, построенная на реальных данных. Черная линия, которая обрамляет гистограмму, — это распределение Пуассона, которое часто применяется для описания продаж. И в данном случае мы видим, что гистограмма очень хорошо совпадает с распределением Пуассона. Но распределений, которые могут подходить, может быть несколько. Например, Нормальное распределение также может подходить для товаров, которые продаются довольно большими объемами. Однако если характер спроса на товар отрывистый, если Вы можете увидеть много дней, в которых продаж не было вообще, — выбор Пуассона или Нормального распределения становится не самым лучшим выбором.

Таким образом, при формировании модели ST нужно быть очень внимательным к тому, какое распределение выбрать, в зависимости от характера спроса на те или иные товары. А теперь давайте вспомним, что у ритейл сетей не один и даже не 10 товаров на полках, а тысячи и десятки тысяч. В таком контексте вручную выбирать распределение для каждого товара не представляется возможным. А если мы хотим оптимизировать цену через ST для нового товара, который ранее вообще не продавался, выбор верной формы распределения становится похоже на гадание на кофейной гуще.

Нюанс 4: моделирование спроса в онлайн и оффлайн ритейле сильно отличается.

Отличается оно тем, что в онлайне открывается доступ к дополнительной информации, недоступной для офлайна: количество просмотров карточки товара.

Отсюда вытекает, что для онлайн ритейла мы можем выбрать, например, бета-распределениеспроса, что позволяет нам учесть, сколько человек посмотрело карточку товара с указанной ценой и сколько из них купило/не купило его. Именно поэтому, ST популярно в онлайн рекомендательных системах. В оффлайне провернуть такой трюк получится, только если устанавливать камеры и напрямую отслеживать, куда смотрят люди в каждый момент времени, что довольно затратно само по себе.

Устанавливаем априорное распределение

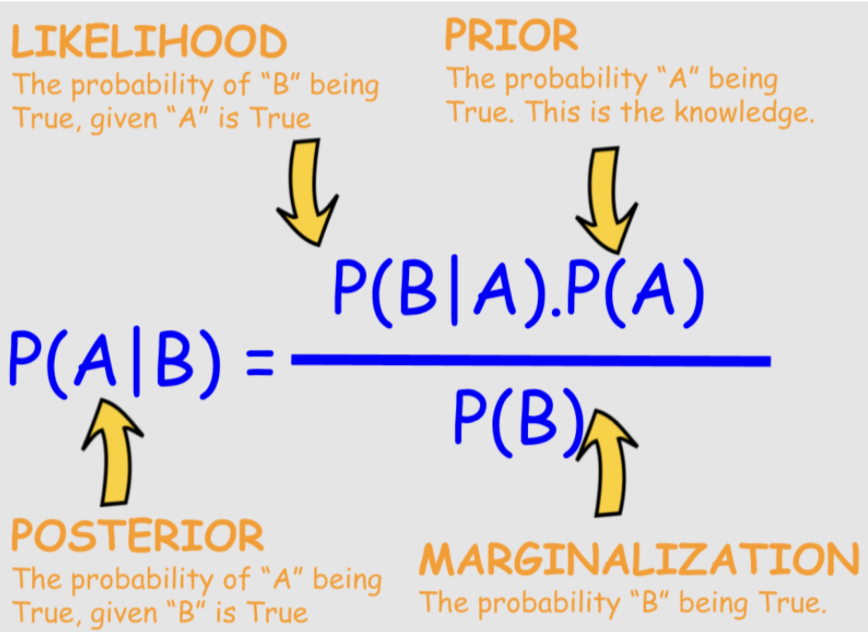
Допустим, мы разрешили все вопросы, описанные на предыдущем этапе, выбрали Гамма распределение для нашей дискретной модели спроса и выбрали возможные цены для установки. Время пришло сделать стартовую версию модели, которая пока ничего не знает о реальном спросе. Для этого нам нужно построить наши ожидания о спросе на товар для каждой возможной цены. В терминах байесовских моделей - установить априорные ожидания (prior).

Нюанс 5: установить априорное распределение - задача нетривиальная.

Для выбранного нами Гамма распределения, для каждой из возможных цен нам нужно установить, какой будет спрос в среднем, для каждой из цен за один период (допустим, мы можем менять цены каждый день). Кажется, вопрос нетривиален и непонятно, как это можно сделать. Мы можем, конечно, пойти посмотреть историю продаж этого товара и попытаться найти эти цены в истории. Однако, во-первых, крайне маловероятно, что мы найдем все цены из выбранного нами перечня, потому что нередки ситуации, когда одна и та же цена может стоять месяцами и никак не меняться. А во-вторых, далеко не факт, что мы продавали по ценам, которые точно соответствуют ценам из нашего списка. Например, если продавали на 5 копеек ниже или выше, то это уже не та же самая цена, а значит, если жестко соблюдать идею дискретной функции спроса (нюанс 1), мы не можем взять эти данные и применить для установления априорной информации для близкой цены.

Самый простой способ решения этой проблемы - установить одинаковую величину спроса для всех цен, например, 1 штука/1 день. Даже если это будет не совсем верно. В конечном счете, для этого и существует ST - постепенно обновить эту априорную информацию через практику и понять, а какая величина спроса для каждой цены на самом деле. Так ведь?

Такой подход при изучении источников, касающихся ST, можно встретить бесчисленное количество раз. И тут кроется ловушка.

Выбираем цену и измеряем спрос

Нюанс 6: неверная установка априорных распределений дорого стоит.

Поскольку задача установления априорных распределений - трудная, то возможны ошибки. Тот кто знаком с формулой Байеса, может сказать - в этом и смысл, что ошибки будут корректироваться при поступлении новой информации. Все так, однако давайте спросим: а насколько больше потребуется итераций, если установить неверную величину априорного спроса? Давайте посмотрим, к чему приводит неверное установление априорных распределений с практической точки зрения. Для этого проведем симуляцию, в которой будем пытаться ставить неправильные априорные вероятности и смотреть на то, как поведет себя алгоритм ST в процессе оптимизации.

import numpy as np

# parameters
prices = [1.99, 2.49, 2.99, 3.49, 3.99, 4.49, 5.99]
alpha_0 = 30.00     # IDEAL parameter of the prior distribution
beta_0 = 1.00       # IDEAL parameter of the prior distribution
T = 500


# parameters of the true (unknown) demand model
true_slop = -7
true_intercept = 50

# prior distribution for each price
p_theta = []
for p in prices:
    p_theta.append({'price': p, 'alpha': alpha_0, 'beta': beta_0})

def sample_actual_demand(price): 
    demand = true_intercept + true_slop * price
    if demand <= 0:
        poisson = 0
    else:
        poisson = np.random.poisson(demand, 1)[0]
    return poisson

# sample mean demands for each price level
def sample_demands_from_model(p_theta):
    return list(map(lambda v: 
           np.random.gamma(v['alpha'], 1/v['beta']), p_theta))

# return price that maximizes the revenue
def optimal_price(prices, demands):
    price_index = np.argmax(np.multiply(prices, demands))
    return price_index, prices[price_index]


prices_setted = []
observed_demand = []

# simulation loop        
for t in range(0, T):
    if t % 7 == 0:
        demands = sample_demands_from_model(p_theta)
        price_index_t, price_t = optimal_price(prices, demands)
        
    prices_setted.append(price_t)
    # offer the selected price and observe demand
    demand_t = sample_actual_demand(price_t)
    observed_demand.append(demand_t)
        
    # update model parameters
    v = p_theta[price_index_t]
    v['alpha'] = v['alpha'] + demand_t
    v['beta'] = v['beta'] + 1

Предположим, что мы занизили возможный спрос в своих ожиданиях и предсказали, что продажи по цене 2.99 будут не 30 шт, а 10 шт.

На графике ниже представлено три блока:

1. Реализованный спрос в шт за каждый день по фактически установленной цене;

2. Цены, которые устанавливал алгоритм ST (синяя линия) и идеальная цена (зеленая);

3. Упущенная выручка (накопительно), которая рассчитывалась как выручка по оптимальной цене минус выручка по фактически установленной цене.

График 5: Ошибаемся в установке априорной информации

Что же мы видим? ST систематически неверно ставит цену в 4.49, приближаясь к оптимальной цене 3.49 слишком медленно. Не хватило даже первых 500 дней (а это примерно 1.5 года). Подробнее про то, как работает ST при установлении неверного априорного распределения, можно почитать тут в разделе “6.1 Prior Distribution Specification”.

Почему так происходит? Давайте рассмотрим упрощенный пример в три последовательных этапа оптимизации цен. Для иллюстративных целей забудем про рандомность распределения.

1 этап. Мы ничего не знаем о спросе, для каждой цены установили априорный спрос в 10 шт.

При оптимизации выручки, мы выбираем цену, при которой у нас наибольшая ожидаемая выручка - 59.9

2 этап. Мы установили эту цену и получили фидбек: по этой цене продалось 9 шт. 

3 этап. Обновляем априорную информацию, заново предсказываем сколько штук будет продаваться по каждой из цен, и видим:

Цена 5.99 повторно становится максимально привлекательной из-за того, что ожидаемая выручка становится вновь самой высокой, и модель будет выбирать и выбирать ее повторно, не пытаясь нащупывать другие цены. Мы видим ровно такое же поведение на графике, когда сэмплирование “застряло” на высоких ценах, слишком медленно подходя к оптимальной цене. Для сравнения, давайте посмотрим на вариант работы модели ST, когда априорная информация установлена на правильном уровне:

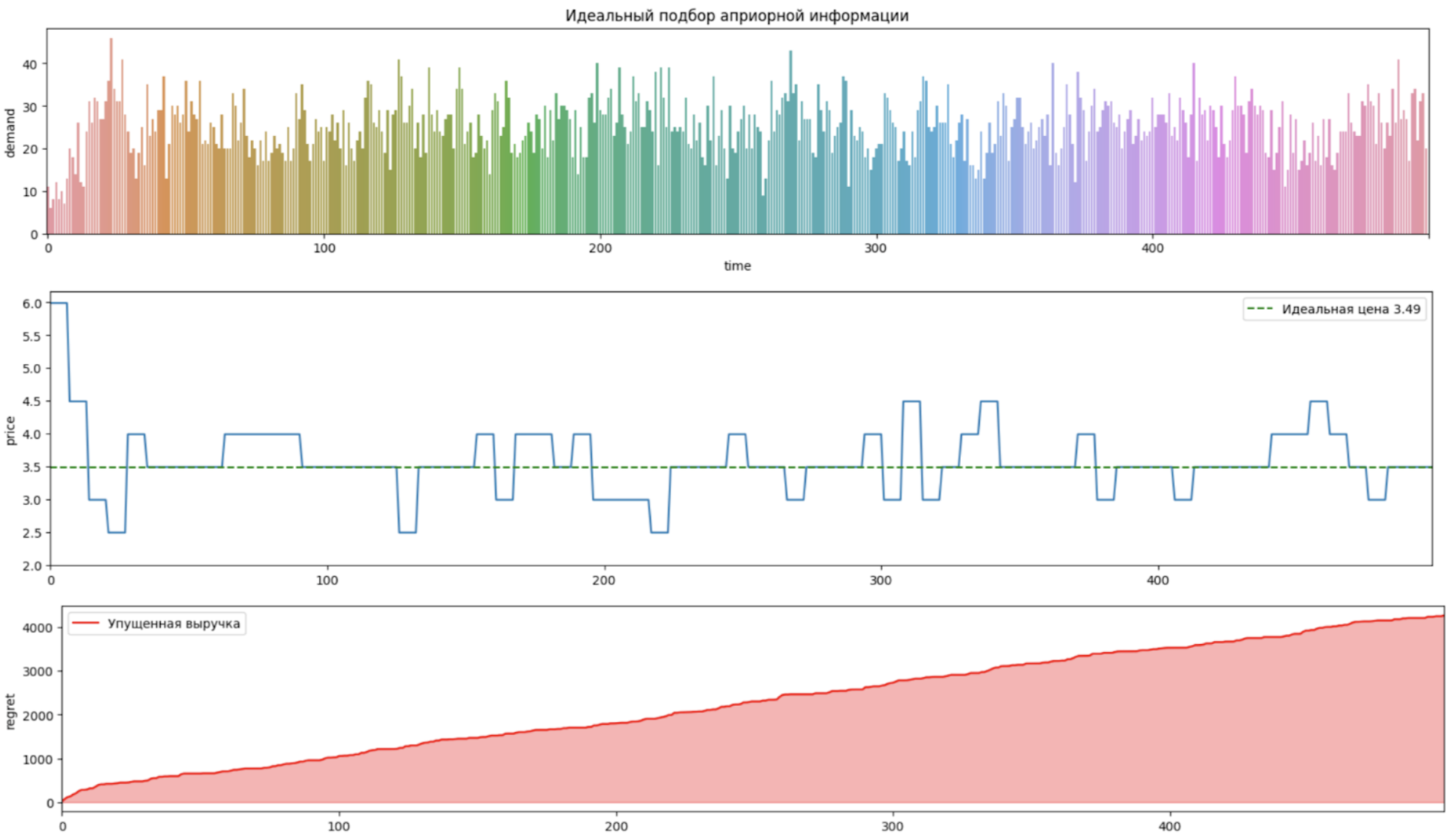
Здесь сразу видно, что модель ST буквально за несколько недель нащупала нужную цену в 3.49 и ставила ее основное время, отклоняясь вверх или вниз, “прощупывая” соседние цены, чтобы убедиться в правильности выбранной цены. Это ровно то поведение модели ST, которое ожидается. В точечных моделях значимая проблема заключается в “застревании” на каких-то определенных, неоптимальных ценах, без способности выйти из этой ситуации через установку каких-то новых цен. Как было продемонстрировано выше, при неправильной настройке априорной информации, ST будет страдать ровно от такого же недуга.

Еще больше неочевидных вещей

Кажется и так уже достаточно, что еще может пойти не так?

Нюанс 7: чем более отрывистый спрос на товар, тем больше времени понадобится на оптимизацию цены через ST.

Предыдущие исследования на симуляторе предполагали, что у нас есть довольно устойчивый спрос (без проседания в 0 в некоторые дни), однако, давайте не забывать, что не все товары могут похвастаться такой статистикой продаж. Как поведет себя ST при условии, что большинство дней остаются вовсе без продаж по товару, а когда продажи есть, то они единичные?

Для этого, изменим условия симулятора: теперь, вместо истинной, линейной кривой спроса, у нас будет вероятность того, будет ли куплен товар для каждой тестируемой цены. Зависимость спроса от цены при этом остается прежней - чем ниже цена, тем вероятность покупки выше. Если “монетка” выпадает на “куплен”, то спрос - 1 шт, в противном случае - 0 шт.

Чтобы ST начал работать при таких условиях, нужно поменять вероятностное распределение на такое, которое учитывает только два возможных варианта (1 и 0). В данном случае, истинный спрос у нас будет подчиняться Биномиальному распределению, что позволяет нам выбрать бета-распределение в качестве априорного.

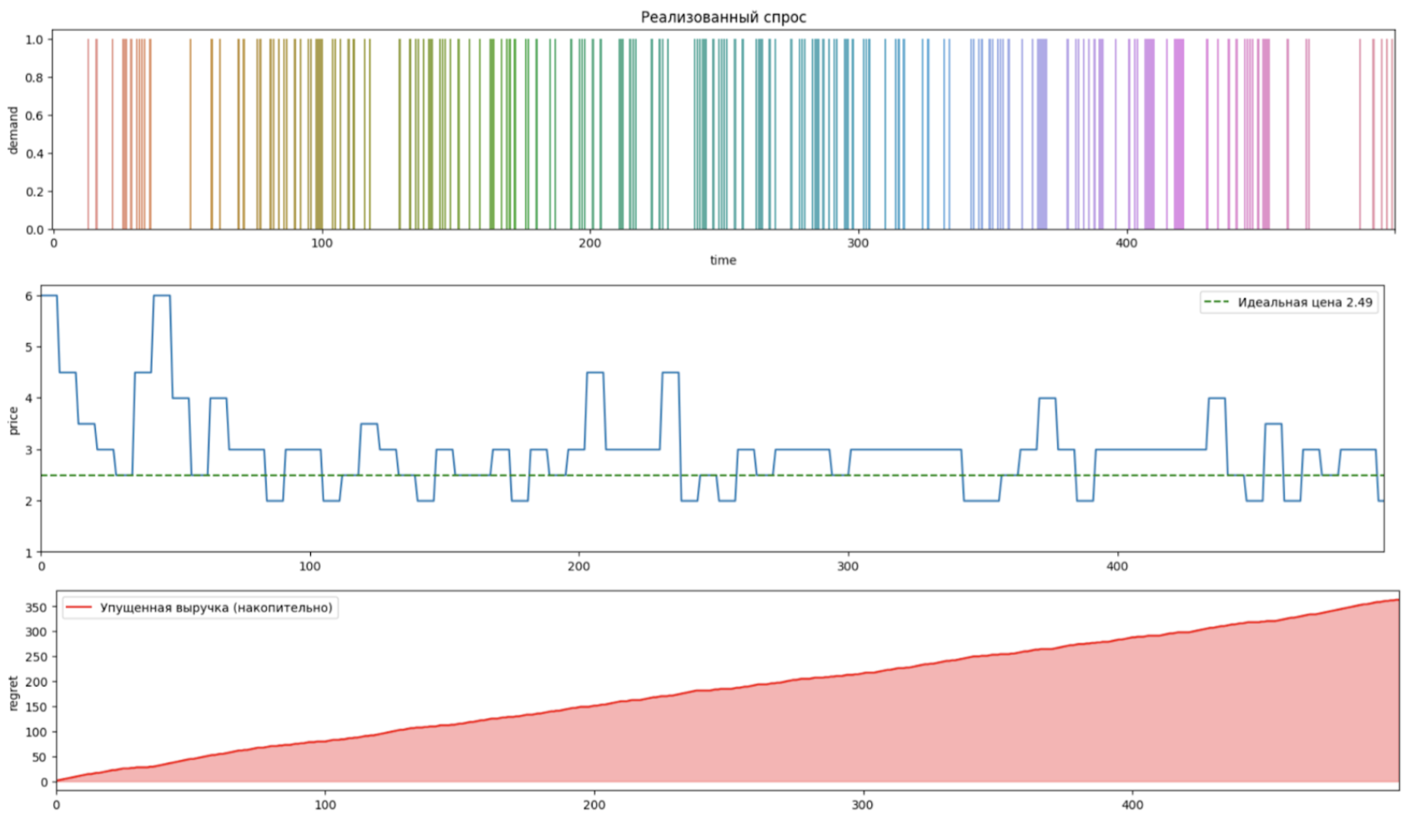
После запуска симуляции мы получили результаты, которые можно интерпретировать как то, что ST не справляется с задачей установления точной оптимальной цены. Вместо этого, устанавливаемые цены колеблются вокруг истинно оптимальной цены даже по прошествии 500 дней. В целом нет оснований полагать, что модель не сойдется когда-то в будущем, но готовы ли Вы ждать >500 дней для выявления оптимальной цены по товару?

Почему так происходит? Ответ довольно очевиден: если у нас товар продается в лучшем случае по 1 шт в неделю, то любая модель будет страдать от того, что она не способна выявить истинную зависимость спроса от цены в течение довольно продолжительного периода времени. Поэтому тут остается только “войти в положение” и понять, что любые модели - это не магия, которая возьмет информацию о кривой спроса из ниоткуда.

Нюанс 8: так ли плохи точечные модели на самом деле?

Ранее уже было описано, что точечные модели при оптимизации цен, влияют сами на себя и из-за этого “застревают” на неоптимальных ценах, даже не пытаясь пробовать альтернативные цены. А что если мы им поможем попробовать разные цены?

В данном иллюстративном примере мы сделаем простую вещь: в первую неделю на симуляторе установим максимально допустимую цену, во вторую неделю - минимально допустимую цену. Назовем это “инициализация”. В качестве ML модели возьмем обычную линейную регрессию, которая будет использоваться в попытке оценить кривую спроса и установить оптимальную цену на основе этой оценки.

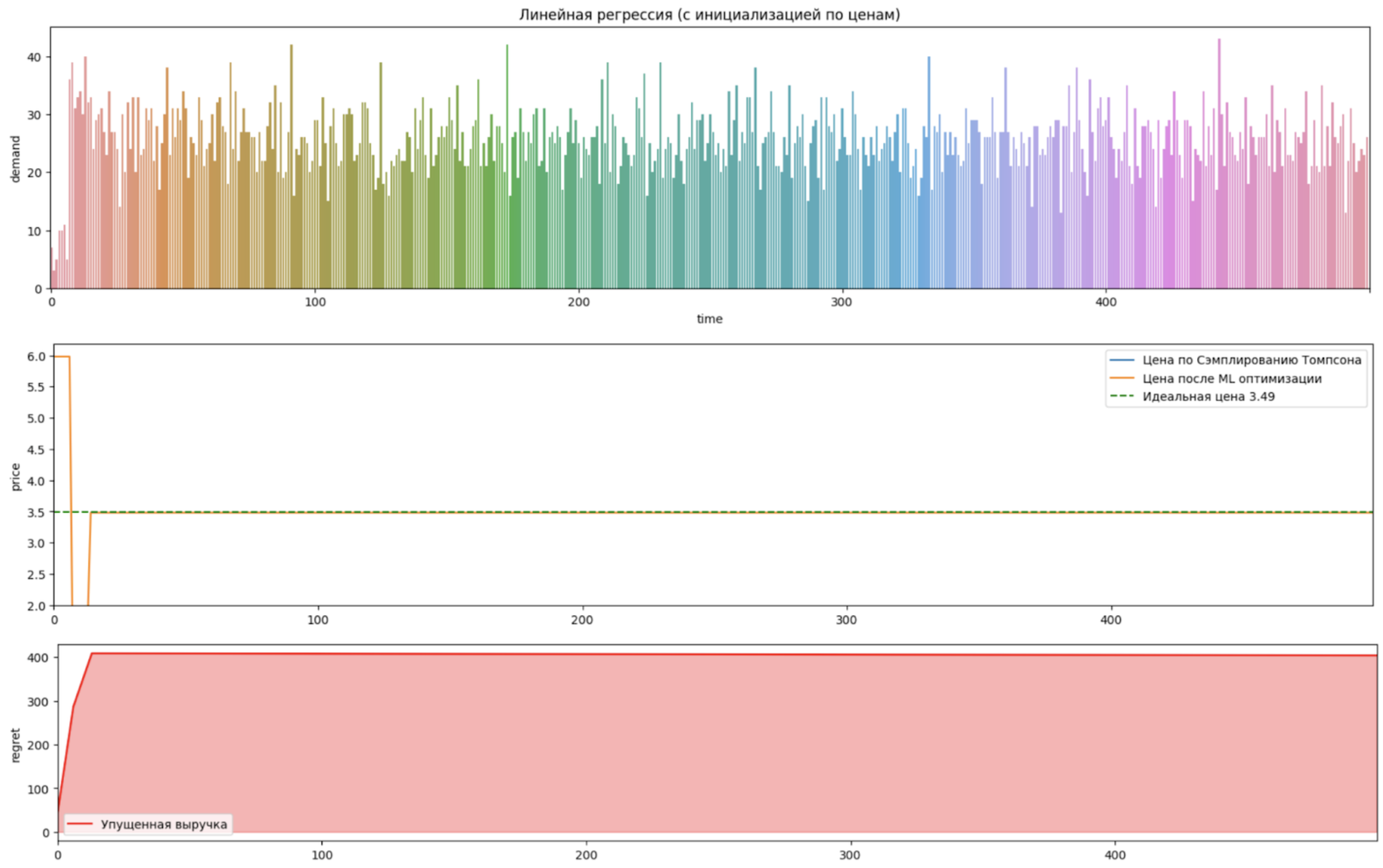
Давайте разберемся, что же мы видим на графике 8. Первые две недели были установлены цены, сперва самая высокая из доступных - 5.99, после нее - самая низкая из доступных - 1.99. Начиная с третьей недели, ML модель могла самостоятельно устанавливать цену, которую она посчитала оптимальной - 3.49 и больше ее не меняла. Обратите внимание, как это отличается от модели ST (график 6), которая подошла к оптимальной цене довольно быстро, однако продолжила пробовать другие цены на всем оставшемся промежутке времени. Также хочется обратить внимание на накопленную потерянную выручку, от установления не оптимальной цены. В случае нашего подхода с ML, график перестал расти после третьей недели, чего нельзя сказать о подходе ST. Почему так произошло? 

Во-первых, хочется напомнить, что одно из заявленных преимуществ ST над точечными ML моделями заключается в том, что ST продолжает “прощупывать” цены, даже после того, как она сошлась к оптимальной цене. Любое “прощупывание” - потеря выручки. Поэтому при применении модели ST нужно быть готовым к тому, что подвижность цен может значительно увеличиться по сравнению с тем, как было до применения каких-либо моделей.

Во-вторых, чем более случайный характер носит спрос, тем сложнее ST определить оптимальную цену. Это продолжает приводить к значительным скачкам в устанавливаемых ценах, что опять-таки приводит к потере выручки на оптимальных ценах.

Почему же тогда ML модель установила сразу же нужную цену? Для этого есть несколько причин:

1. Мы установили цены в широком диапазоне, протестировали на них спрос и благодаря этому стало возможно построить линейную модель, которая успешно предсказала спрос на всем диапазоне цен между установленными ценами, что позволило выбрать сразу же оптимальную цену.

2. Несмотря на то, что спрос тут вероятностная величина и модель не со 100% точностью определила коэффициент перед фактором цена, тем не менее, этого хватило, чтобы найти оптимальную цену из перечня доступных для установки.

3. Вернемся к дискретному спросу в модели ST еще раз: трюк, который мы проделали только что, слабо бы помог ST найти оптимальную цену в случае дискретной модели спроса, потому что спрос для каждой цены там предполагается независимым. То есть информацию о спросе по другим ценам нельзя использовать для прогнозирования спроса по ценам, которые еще не выставлялись (по крайней мере, в классическом ST).

В качестве выводов

В данной статье мы попытались рассмотреть практические проблемы применения модели RL/ST для оптимизации цен, чтобы доказать, что RL/ST - не волшебная палочка и точно также требует глубокой проработки, как и ML подход. Значительное количество проблем оказалось связано с выбором дискретной модели спроса, которая не позволяет учитывать весь перечень внешних факторов, влияющих на спрос, а также, не позволяющая делиться информацией о спросе с “соседними ценами”. 

Чтобы преодолеть это, можно посмотреть в сторону контекстных многоруких бандитов. В данном случае учитывается не только распределение самой предсказываемой величины, но и “контекст”, который влияет на конечное распределение. Это позволяет значительно уточнить предсказания модели и сойтись модели ST значительно быстрее. Вот несколько примеров того как могут быть модифицированы модели деревьев решений и нейронной сети для использования в модели ST. Про линейных контекстных бандитов также не забываем. Как видите, мы вновь вернулись к ML моделям, хоть и в модифицированном виде, который позволяет предсказывать возможное распределение величин, вместо одной конкретной точки.